The University of Iowa 22 c 296 Automated









![Verification conditions: assignment A) B) [g(X, Y)/Y] A): x 1>=0 / x 2>=0 B): Verification conditions: assignment A) B) [g(X, Y)/Y] A): x 1>=0 / x 2>=0 B):](https://slidetodoc.com/presentation_image_h2/53e3fe6b919085c49de9350556f483ca/image-18.jpg)








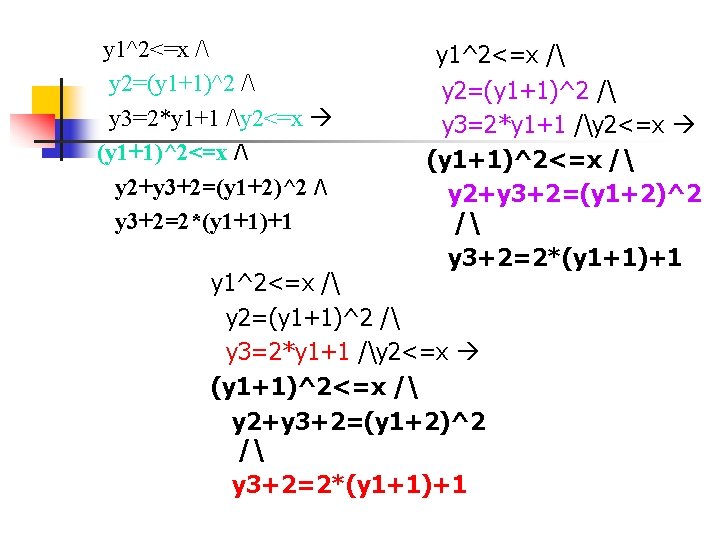






- Slides: 53

The University of Iowa 22 c: 296 Automated Software Verification of Flowchart Programs Copyright 2003 -04, Doron Peled and Cesare Tinelli. These notes are based on a set of lecture notes originally developed by Doron Peled at the University of Warwick. These notes are copyrighted materials and may not be used in other course settings outside of the University of Iowa in their current form or modified form without the express written permission of the copyright holders. During this course, students are prohibited from selling notes to or being paid for taking notes by any person or commercial firm without the express written permission of the copyright holders.

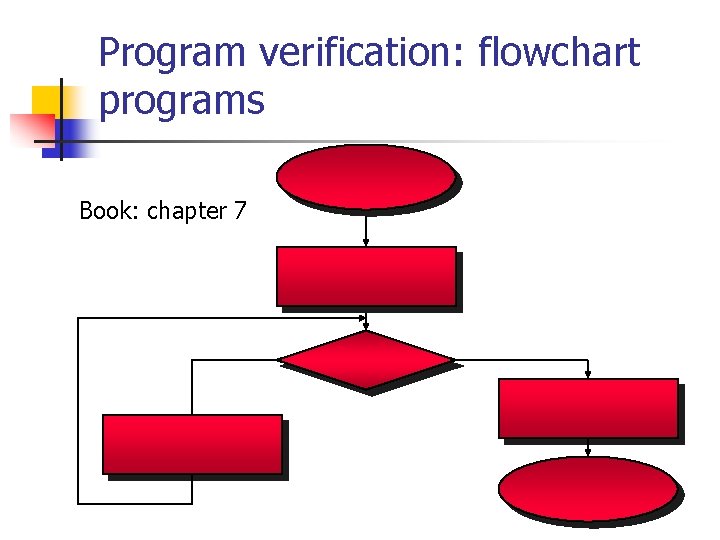
Program verification: flowchart programs Book: chapter 7

History n n Verification of flowchart programs: Floyd, 1967 Hoare’s logic: Hoare, 1969 Linear Temporal Logic: Pnueli, Krueger, 1977 Model Checking: Clarke & Emerson, 1981

Program Verification n n n Predicate (first order) logic. Partial correctness, Total correctness Flowchart programs Invariants, annotated programs Well founded ordering (for termination) Hoare’s logic

Predicate (first order logic) n Variables, functions, predicates n Terms n Formulas (assertions)

Signature Variables: v 1, x, y 18 Each variable represents a value of some given domain (int, real, string, …). n Function symbols: f(_, _), g 2(_), h(_, _, _). Each function has an arity (number of paramenters), a domain for each parameter, and a range. f: int*int->int (e. g. , addition), g: real->real (e. g. , square root) A constant is a predicate with arity 0. n Relation symbols: R(_, _), Q(_). Each relation has an arity, and a domain for each parameter. R : real*real (e. g. , greater than). Q : int (e. g. , is a prime). n

Terms are objects that have values. n Each variable is a term. n Applying a function with arity n to n terms results in a new term. Examples: v 1, 5. 0, f(v 1, 5. 0), g 2(f(v 1, 5. 0)) n More familiar notation: sqr(v 1+5. 0)

Formulas Applying predicates to terms results in a formula. R(v 1, 5. 0), Q(x) More familiar notation: v 1>5. 0 n One can combine formulas with the boolean operators (and, or, not, implies). R(v 1, 5. 0)->Q(x) x>1 -> x*x>x n One can apply existential and universal quantification to formulas. x Q(X) x 1 R(x 1, 5. 0) X Y R(x, y) n

Models, Proofs n n n A model gives a meaning (semantics) to a first order formula: n A relation for each relation symbol. n A function for each function symbol. n A value for each variable. An important concept in first order logic is that of a proof. We assume the ability to prove that a formula holds for a given model. Example proof rule (MP) :

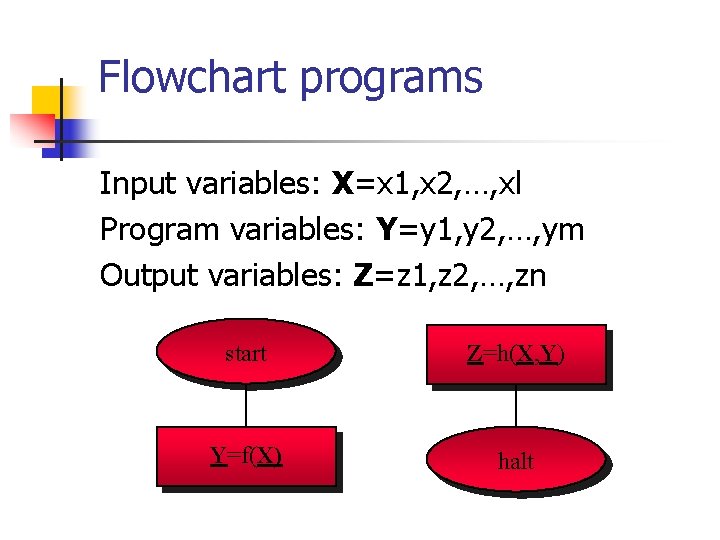
Flowchart programs Input variables: X=x 1, x 2, …, xl Program variables: Y=y 1, y 2, …, ym Output variables: Z=z 1, z 2, …, zn start Z=h(X, Y) Y=f(X) halt

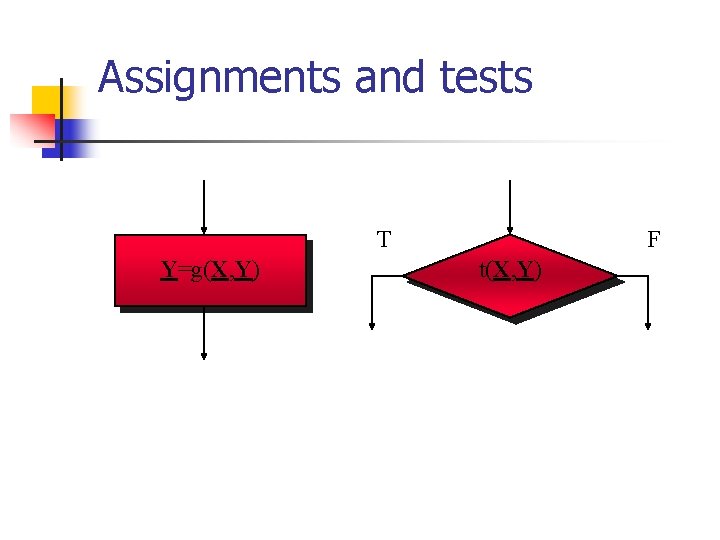
Assignments and tests T Y=g(X, Y) F t(X, Y)

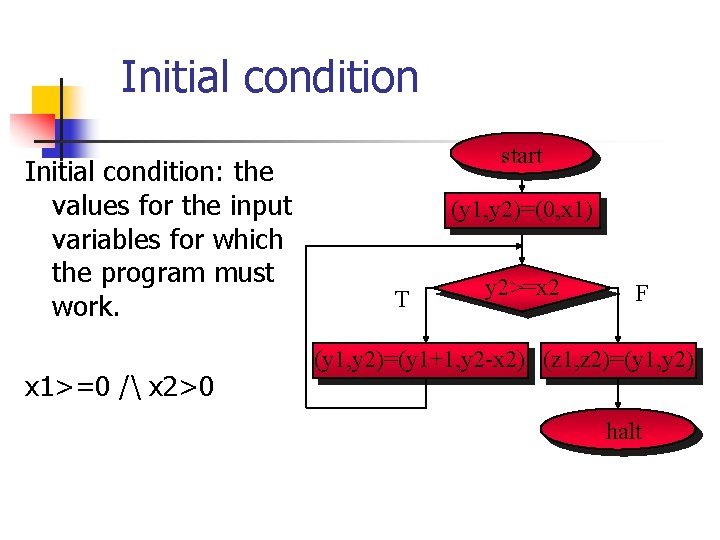
Initial condition: the values for the input variables for which the program must work. x 1>=0 / x 2>0 start (y 1, y 2)=(0, x 1) T y 2>=x 2 F (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) halt

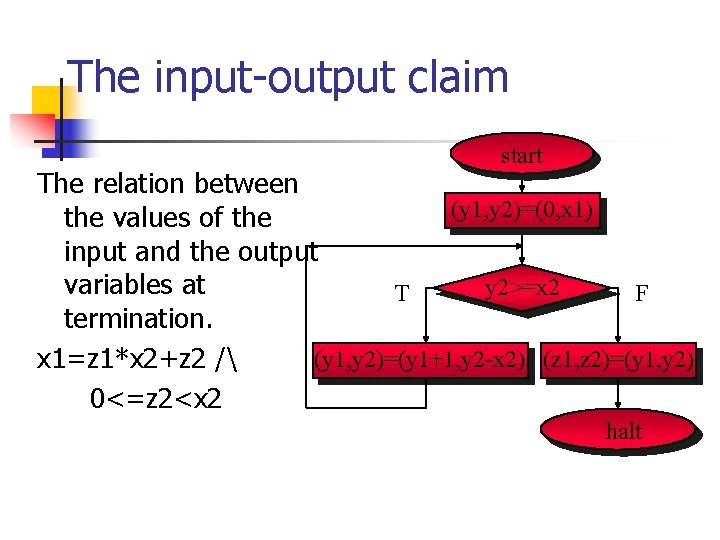
The input-output claim start The relation between (y 1, y 2)=(0, x 1) the values of the input and the output variables at y 2>=x 2 T F termination. (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) x 1=z 1*x 2+z 2 / 0<=z 2<x 2 halt

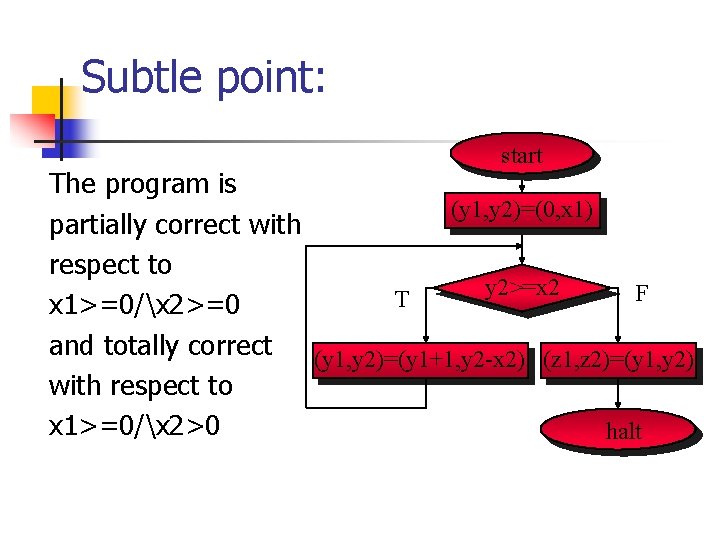
Partial correctness, Termination, Total correctness n n n Partial correctness: if the initial condition holds and the program terminates then the input-output claim holds. Termination: if the initial condition holds, the program terminates. Total correctness: if the initial condition holds, the program terminates and the input-output claim holds.

Subtle point: start The program is (y 1, y 2)=(0, x 1) partially correct with respect to y 2>=x 2 F T x 1>=0/x 2>=0 and totally correct (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) with respect to x 1>=0/x 2>0 halt

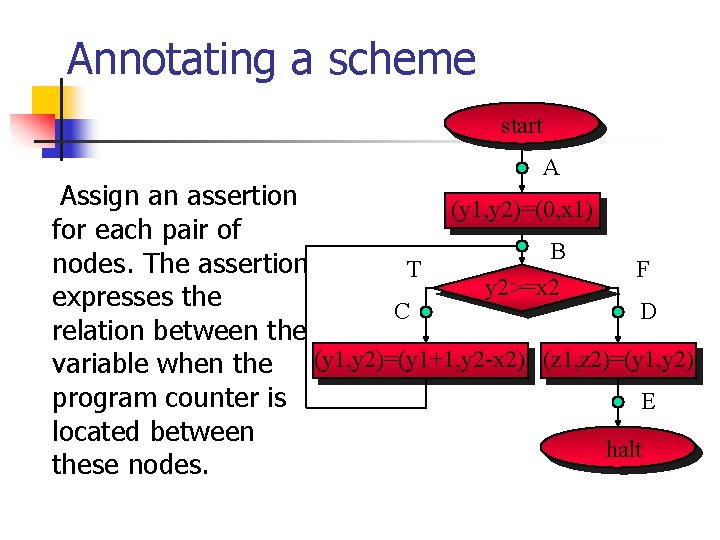
Annotating a scheme start A Assign an assertion (y 1, y 2)=(0, x 1) for each pair of B nodes. The assertion T F y 2>=x 2 expresses the C D relation between the (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) variable when the program counter is E located between halt these nodes.

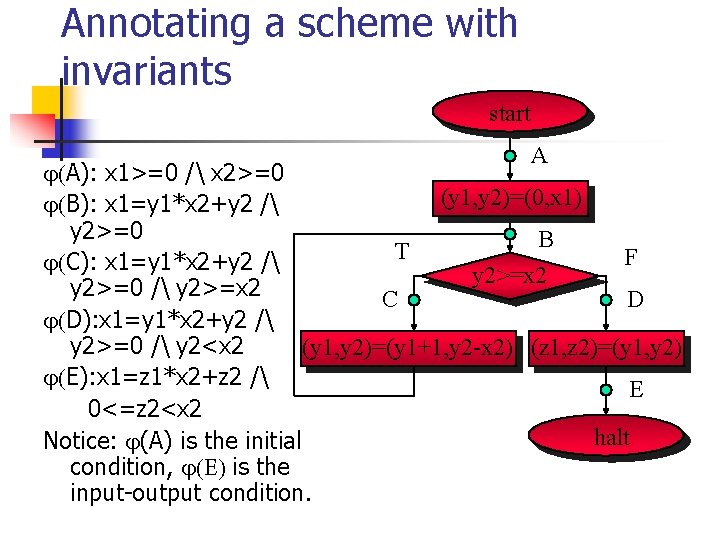
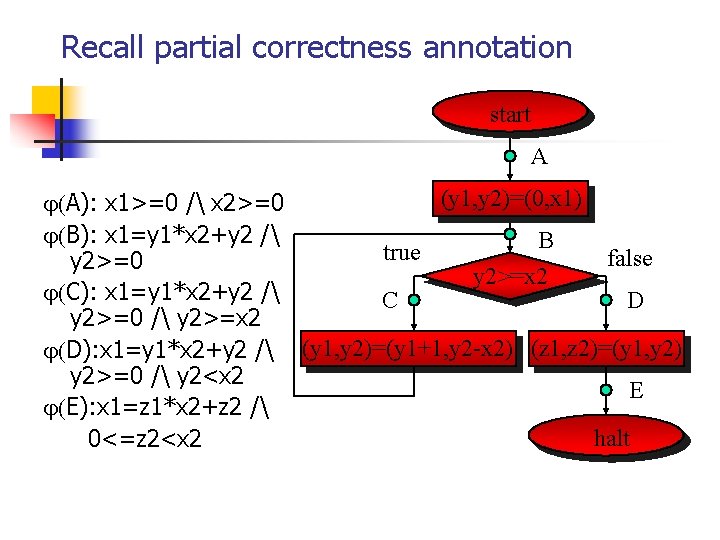
Annotating a scheme with invariants start A A): x 1>=0 / x 2>=0 (y 1, y 2)=(0, x 1) B): x 1=y 1*x 2+y 2 / y 2>=0 B T F C): x 1=y 1*x 2+y 2 / y 2>=x 2 y 2>=0 / y 2>=x 2 C D D): x 1=y 1*x 2+y 2 / y 2>=0 / y 2<x 2 (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) E): x 1=z 1*x 2+z 2 / E 0<=z 2<x 2 halt Notice: (A) is the initial condition, is the input-output condition.
![Verification conditions assignment A B gX YY A x 10 x 20 B Verification conditions: assignment A) B) [g(X, Y)/Y] A): x 1>=0 / x 2>=0 B):](https://slidetodoc.com/presentation_image_h2/53e3fe6b919085c49de9350556f483ca/image-18.jpg)
Verification conditions: assignment A) B) [g(X, Y)/Y] A): x 1>=0 / x 2>=0 B): x 1=y 1*x 2+y 2 / y 2>=0 B) [g(X, Y )/Y] = x 1=0*x 2+x 1 / x 1>=0 A (y 1, y 2)=(0, x 1) Y=g(X, Y) B A (y 1, y 2)=(0, x 1) B

Second assignment C (y 1, y 2)=(y 1+1, y 2 -x 2) B C): x 1=y 1*x 2+y 2 / y 2>=0 / y 2>=x 2 B): x 1=y 1*x 2+y 2 / y 2>=0 B)[g(X, Y)/Y]: x 1=(y 1+1)*x 2+y 2 -x 2 / y 2 -x 2>=0

Third assignment D (z 1, z 2)=(y 1, y 2) E D): x 1=y 1*x 2+y 2 / y 2>=0 / y 2<x 2 E): x 1=z 1*x 2+z 2 / 0<=z 2<x 2 E)[g(X, Y)/Z]: x 1=y 1*x 2+y 2 / 0<=y 2<x 2

Verification conditions: tests T B) / t(X, Y) C) B) /¬t(X, Y) D) C B): x 1=y 1*x 2+y 2 / y 2>=0 C): x 1=y 1*x 2+y 2 / T y 2>=0 / y 2>=x 2 C D): x 1=y 1*x 2+y 2 / y 2>=0 / y 2<x 2 B t(X, Y) F D B y 2>=x 2 F D

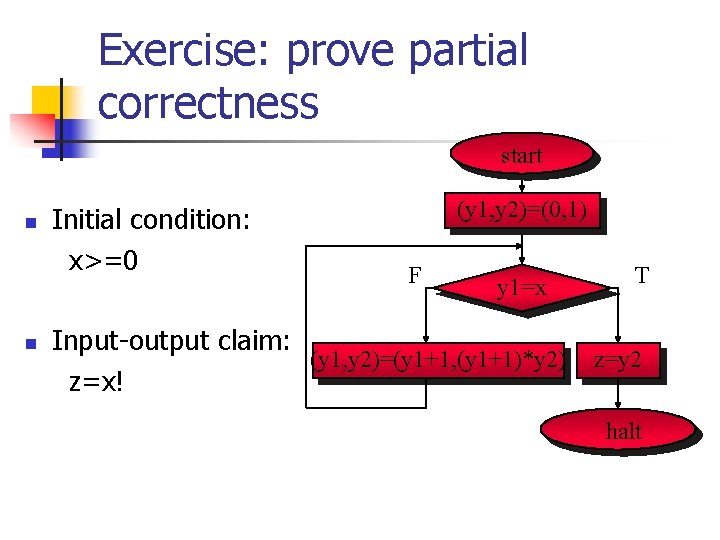
Exercise: prove partial correctness start n n Initial condition: x>=0 (y 1, y 2)=(0, 1) F y 1=x T Input-output claim: (y 1, y 2)=(y 1+1, (y 1+1)*y 2) z=y 2 z=x! halt

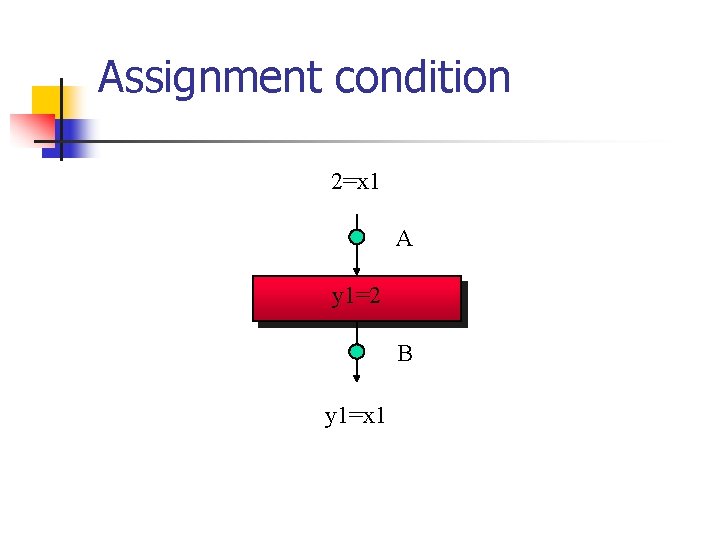
Assignment condition 2=x 1 A (y 1, y 2)=(0, x 1) y 1=2 B y 1=x 1

Another way to understand assignment conditions Use two versions of variables: before assignment and after. E. g. , y 1 and y 1’, respectively. postcondition: y 1’=x 1 assignment: y 1’=2 precondition: 2=x 1 A (y 1, y 2)=(0, x 1) y 1=2 B y 1=x 1

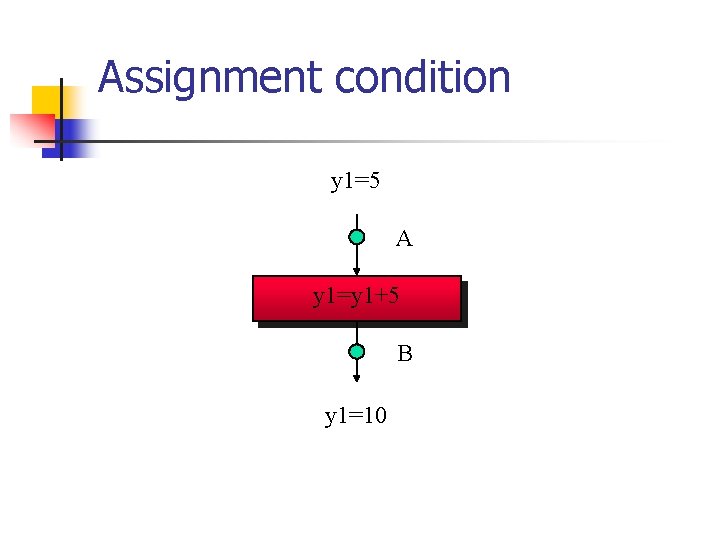
Assignment condition y 1=5 A (y 1, y 2)=(0, x 1) y 1=y 1+5 B y 1=10

Assignment condition Postcondition: y 1’=10 y 1=5 A Assignment: y 1’=y 1+5 Precondition: y 1+5=10, I. e. , y 1=5 (y 1, y 2)=(0, x 1) y 1=y 1+5 B y 1=10

Verification conditions: assignment B): x 1=y 1’*x 2+y 2’ / y 2’ >=0 A): x 1>=0 / x 2>=0 A Assignment: y 1’=0 / y 2’=x 1 B) [g(X, Y)/Y] = x 1=0*x 2+x 1 / x 1>=0 (or simply x 1>=0) (y 1, y 2)=(0, x 1) B

Second assignment Precondition: B): x 1=y 1*x 2+y 2 / y 2>=0 Assignment: y 1’=y 1+1/y 2’=y 2 -x 2 C (y 1, y 2)=(y 1+1, y 2 -x 2) B Postcondition: B)[g(X, Y)/Y]: x 1=(y 1+1)*x 2+y 2 -x 2 / y 2 -x 2>=0

What have we achieved? n n n For each statement S that appears between points X and Y we showed that if the control is in X when (X) holds and S is executed, then (Y) holds. Initially, we know that (A) holds. The above two conditions can be combined into an induction on the number of statements that were executed: n If after n steps we are at point X, then (X) holds.

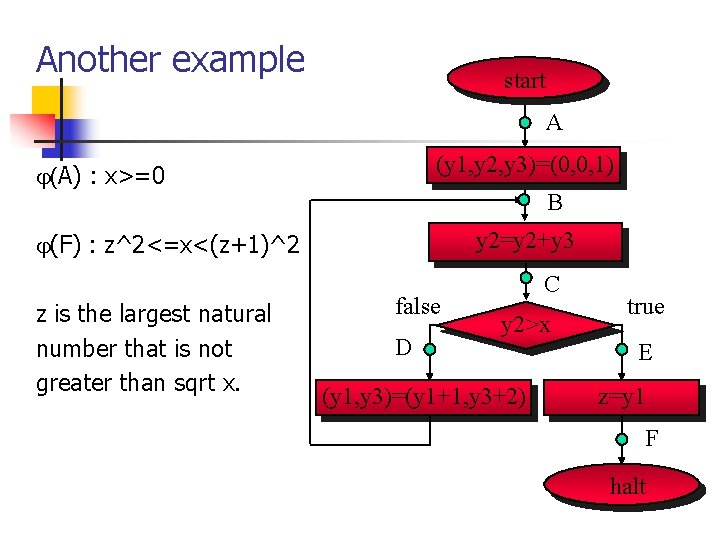
Another example start A (y 1, y 2, y 3)=(0, 0, 1) (A) : x>=0 B y 2=y 2+y 3 (F) : z^2<=x<(z+1)^2 z is the largest natural number that is not greater than sqrt x. false D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

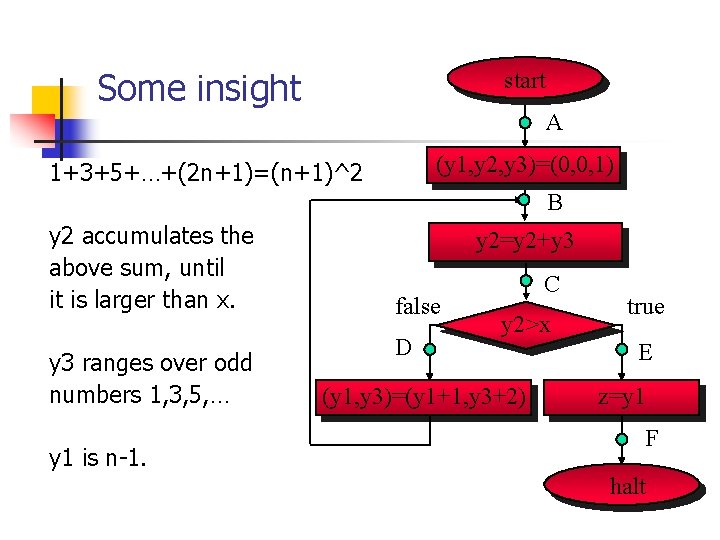
Some insight start A (y 1, y 2, y 3)=(0, 0, 1) 1+3+5+…+(2 n+1)=(n+1)^2 B y 2 accumulates the above sum, until it is larger than x. y 3 ranges over odd numbers 1, 3, 5, … y 1 is n-1. y 2=y 2+y 3 false D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

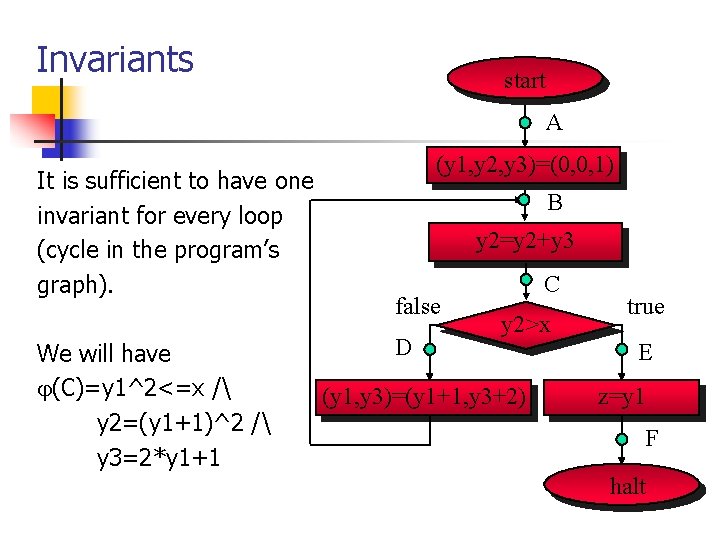
Invariants start A It is sufficient to have one invariant for every loop (cycle in the program’s graph). We will have (C)=y 1^2<=x / y 2=(y 1+1)^2 / y 3=2*y 1+1 (y 1, y 2, y 3)=(0, 0, 1) B y 2=y 2+y 3 false D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

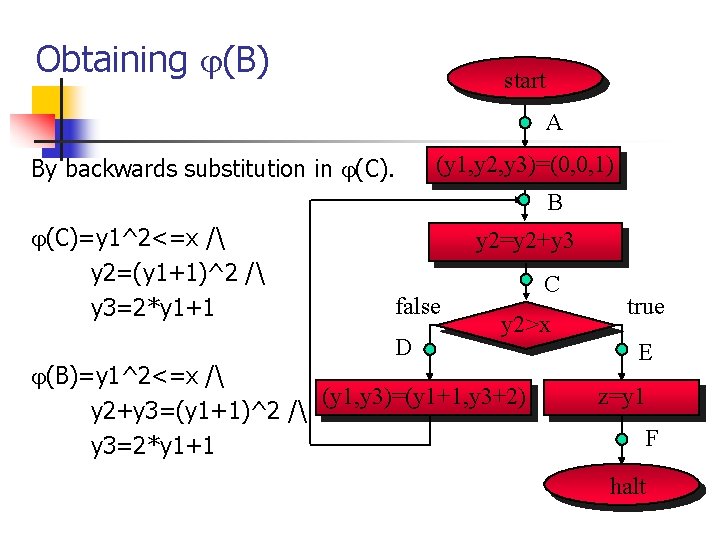
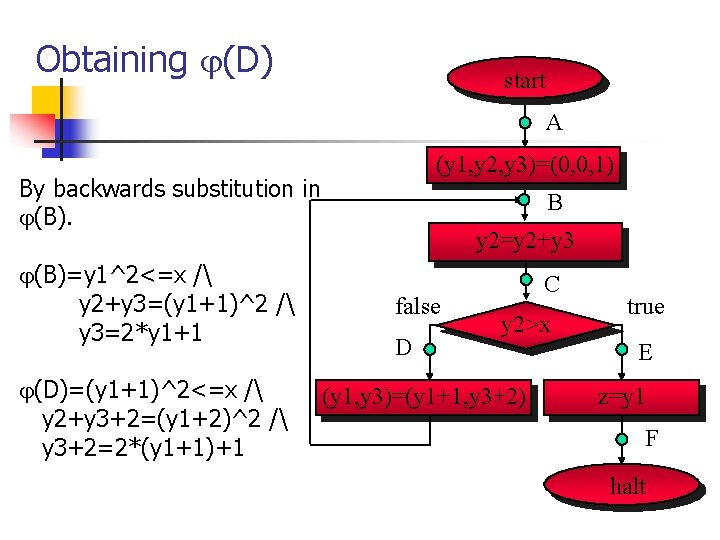
Obtaining (B) start A By backwards substitution in (C). (y 1, y 2, y 3)=(0, 0, 1) B (C)=y 1^2<=x / y 2=(y 1+1)^2 / y 3=2*y 1+1 y 2=y 2+y 3 false D C y 2>x (B)=y 1^2<=x / (y 1, y 3)=(y 1+1, y 3+2) y 2+y 3=(y 1+1)^2 / y 3=2*y 1+1 true E z=y 1 F halt

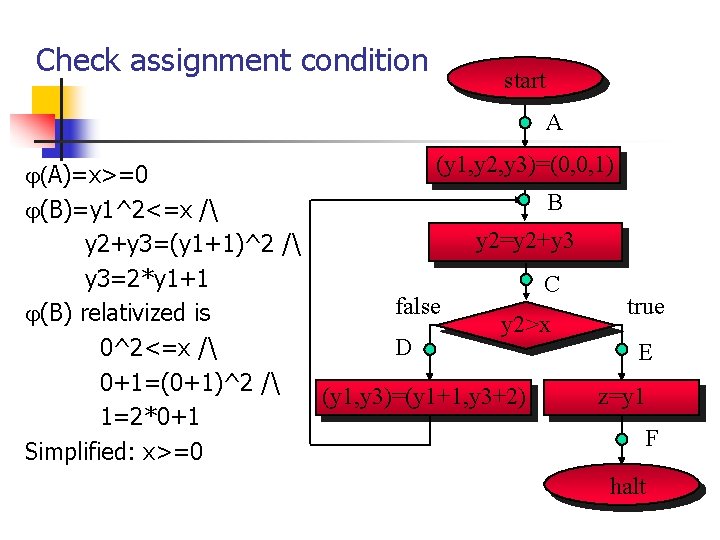
Check assignment condition start A (y 1, y 2, y 3)=(0, 0, 1) (A)=x>=0 B (B)=y 1^2<=x / y 2=y 2+y 3=(y 1+1)^2 / y 3=2*y 1+1 C false true (B) relativized is y 2>x D 0^2<=x / E 0+1=(0+1)^2 / (y 1, y 3)=(y 1+1, y 3+2) z=y 1 1=2*0+1 F Simplified: x>=0 halt

Obtaining (D) start A (y 1, y 2, y 3)=(0, 0, 1) By backwards substitution in (B)=y 1^2<=x / y 2+y 3=(y 1+1)^2 / y 3=2*y 1+1 (D)=(y 1+1)^2<=x / y 2+y 3+2=(y 1+2)^2 / y 3+2=2*(y 1+1)+1 B y 2=y 2+y 3 false D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

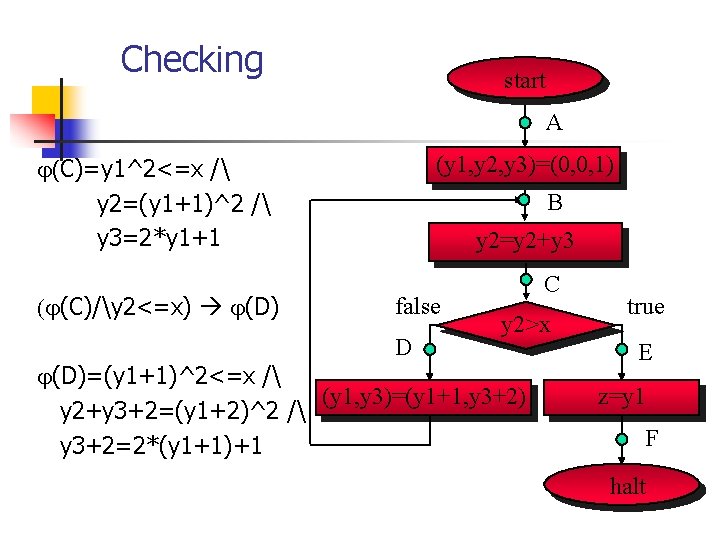
Checking start A (y 1, y 2, y 3)=(0, 0, 1) (C)=y 1^2<=x / y 2=(y 1+1)^2 / y 3=2*y 1+1 (C)/y 2<=x) (D) B y 2=y 2+y 3 false D C y 2>x (D)=(y 1+1)^2<=x / (y 1, y 3)=(y 1+1, y 3+2) y 2+y 3+2=(y 1+2)^2 / y 3+2=2*(y 1+1)+1 true E z=y 1 F halt
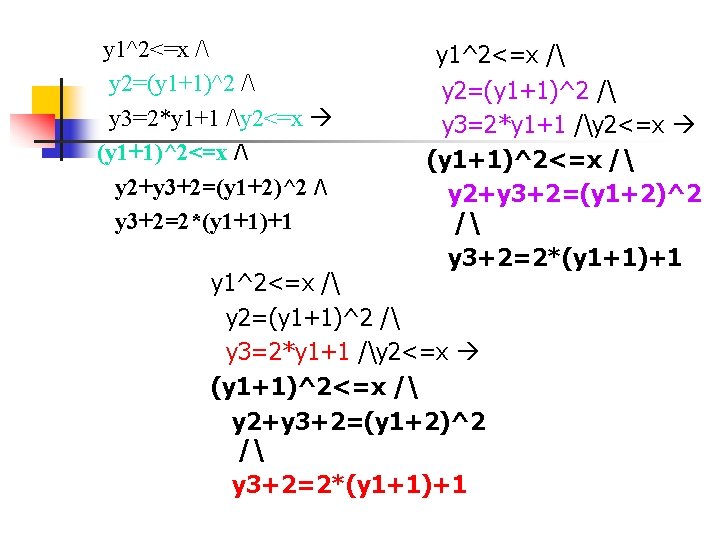
y 1^2<=x / y 2=(y 1+1)^2 / y 3=2*y 1+1 /y 2<=x (y 1+1)^2<=x / y 2+y 3+2=(y 1+2)^2 / y 3+2=2*(y 1+1)+1

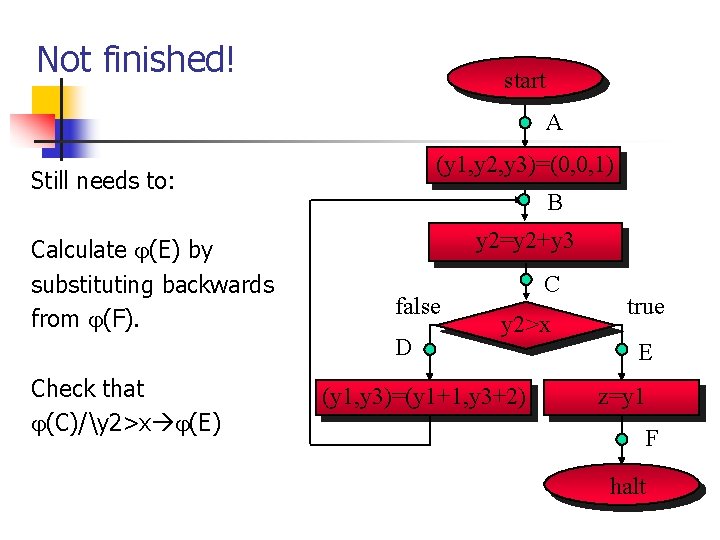
Not finished! start A (y 1, y 2, y 3)=(0, 0, 1) Still needs to: Calculate (E) by substituting backwards from (F). B y 2=y 2+y 3 false D Check that (C)/y 2>x (E) C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

Proving termination

Well-founded sets n n Partially ordered set (W, >): n If a>b and b>c then a>c (transitivity). n If a>b then not b>a (asymmetry). n Not a>a (irreflexivity). Well-founded set (W, >): n Partially ordered. n No infinite decreasing chain a 1>a 2>a 3>…

Examples for well founded sets n n Natural numbers with the larger than (>) relation. Finite sets with the set inclusion ( ) relation. Strings with the superstring relation. Tuples with lexicographic ordering: n n (a 1, b 1)>(a 2, b 2) iff a 1>a 2 or [a 1=a 2 and b 1>b 2]. (a 1, b 1, c 1)>(a 2, b 2, c 2) iff a 1>a 2 or [a 1=a 2 and b 1>b 2] or [a 1=a 2 and b 1=b 2 and c 1>c 2].

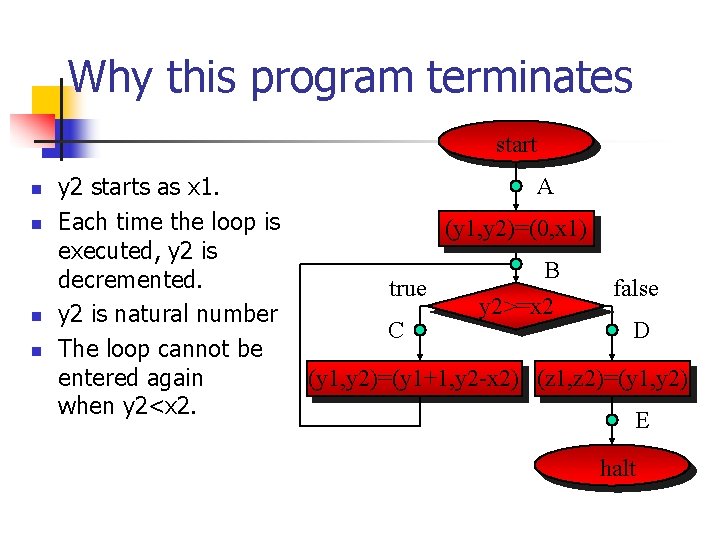
Why this program terminates start n n y 2 starts as x 1. Each time the loop is executed, y 2 is decremented. y 2 is natural number The loop cannot be entered again when y 2<x 2. A (y 1, y 2)=(0, x 1) true C B y 2>=x 2 false D (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) E halt

Proving termination n n Choose a well-founded set (W, >). Attach a function u(N) to each point N. Annotate the flowchart with invariants, and prove their consistency conditions. Prove that (N) (u(N) in W).

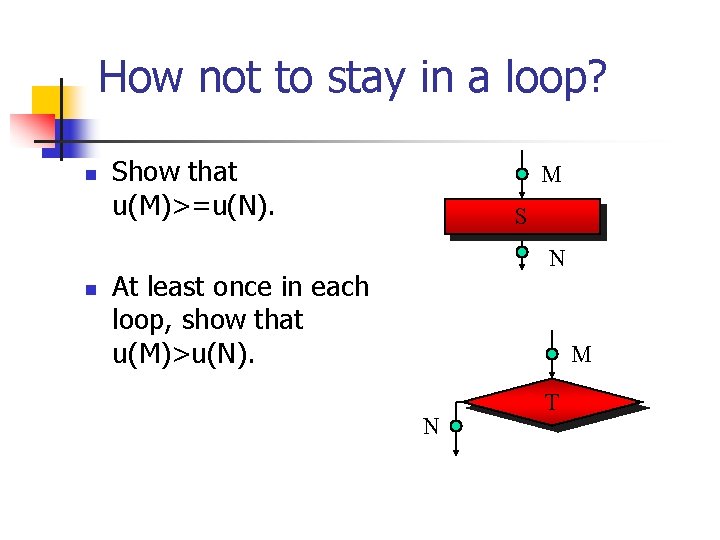
How not to stay in a loop? n n Show that u(M)>=u(N). M S N At least once in each loop, show that u(M)>u(N). M N T

How not to stay in a loop? M For assmt: (M) (u(M)>=u(rel(N)) n assmt N For test (true side): ( (M)/test) (u(M)>=u(N)) n For test (false side): ( (M)/¬test) (u(M)>=u(L)) n M true false test N L

What did we achieve? n n There are finitely many control points. The value of the function u cannot increase. If we return to the same control point, the value of u must decrease (its a loop!). The value of u can decrease only a finite number of times.

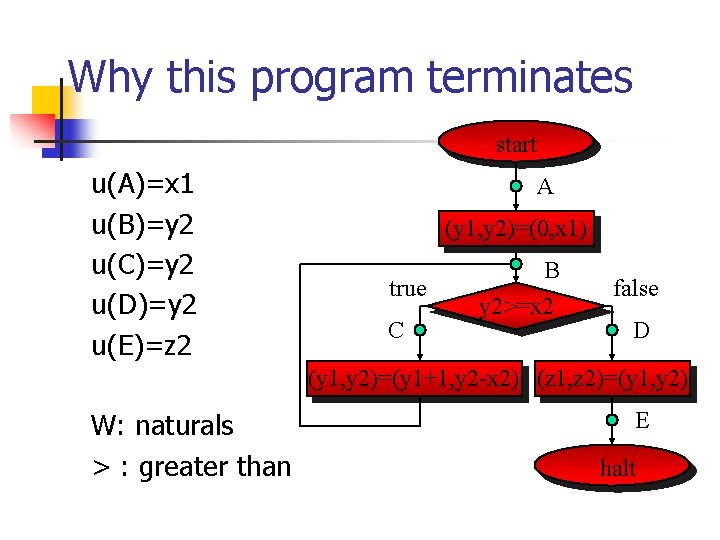
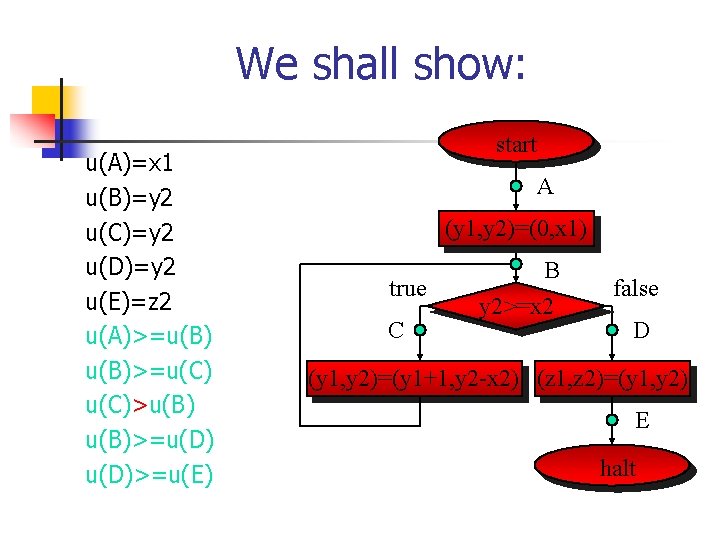
Why this program terminates start u(A)=x 1 u(B)=y 2 u(C)=y 2 u(D)=y 2 u(E)=z 2 A (y 1, y 2)=(0, x 1) true C B y 2>=x 2 false D (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) W: naturals > : greater than E halt

Recall partial correctness annotation start A (y 1, y 2)=(0, x 1) A): x 1>=0 / x 2>=0 B): x 1=y 1*x 2+y 2 / B true false y 2>=0 y 2>=x 2 C): x 1=y 1*x 2+y 2 / C D y 2>=0 / y 2>=x 2 D): x 1=y 1*x 2+y 2 / (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) y 2>=0 / y 2<x 2 E E): x 1=z 1*x 2+z 2 / halt 0<=z 2<x 2

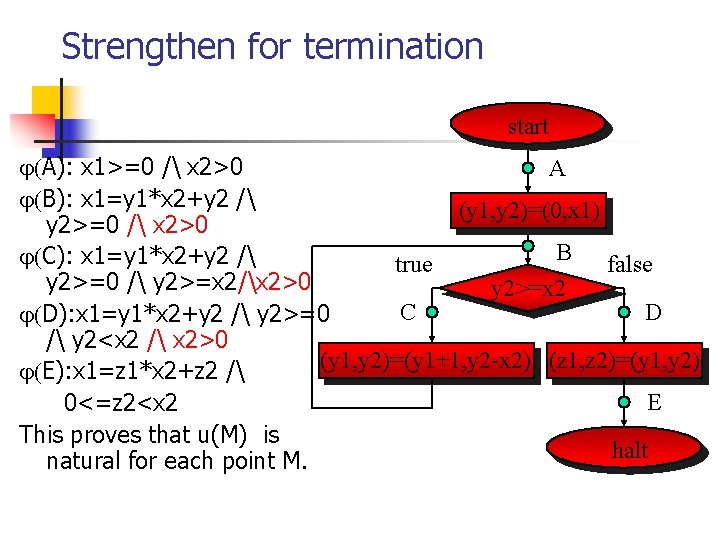
Strengthen for termination start A): x 1>=0 / x 2>0 A B): x 1=y 1*x 2+y 2 / (y 1, y 2)=(0, x 1) y 2>=0 / x 2>0 B false C): x 1=y 1*x 2+y 2 / true y 2>=0 / y 2>=x 2/x 2>0 y 2>=x 2 C D D): x 1=y 1*x 2+y 2 / y 2>=0 / y 2<x 2 / x 2>0 (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) E): x 1=z 1*x 2+z 2 / E 0<=z 2<x 2 This proves that u(M) is halt natural for each point M.

We shall show: u(A)=x 1 u(B)=y 2 u(C)=y 2 u(D)=y 2 u(E)=z 2 u(A)>=u(B)>=u(C)>u(B)>=u(D)>=u(E) start A (y 1, y 2)=(0, x 1) true C B y 2>=x 2 false D (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) E halt

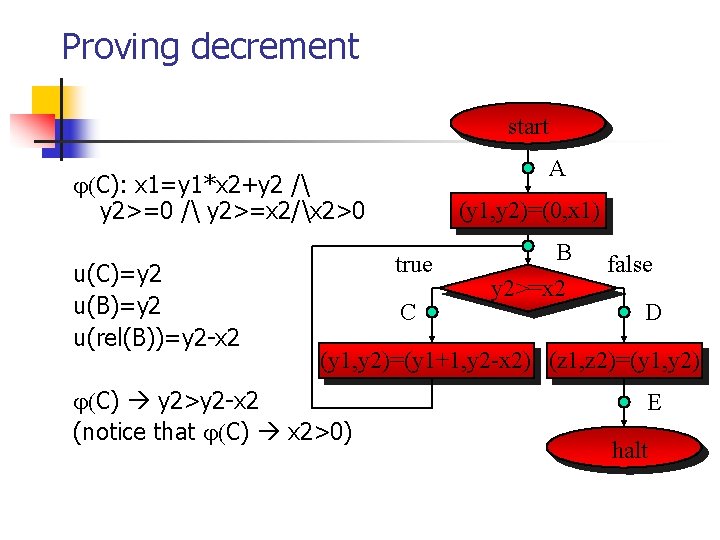
Proving decrement start A C): x 1=y 1*x 2+y 2 / y 2>=0 / y 2>=x 2/x 2>0 u(C)=y 2 u(B)=y 2 u(rel(B))=y 2 -x 2 (y 1, y 2)=(0, x 1) true C B y 2>=x 2 false D (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) C) y 2>y 2 -x 2 (notice that C) x 2>0) E halt

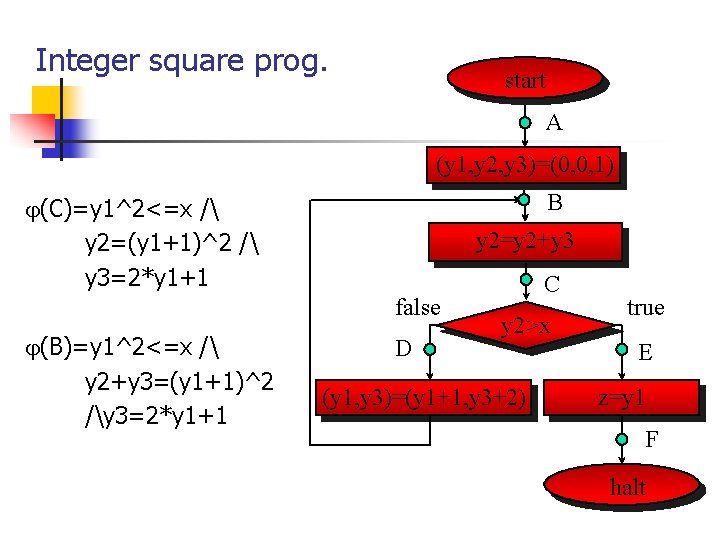
Integer square prog. start A (y 1, y 2, y 3)=(0, 0, 1) B (C)=y 1^2<=x / y 2=(y 1+1)^2 / y 3=2*y 1+1 y 2=y 2+y 3 false (B)=y 1^2<=x / y 2+y 3=(y 1+1)^2 /y 3=2*y 1+1 D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

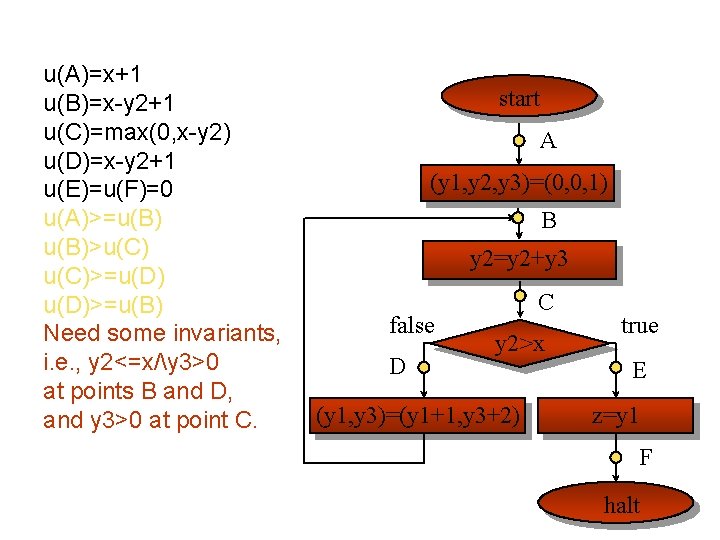
u(A)=x+1 u(B)=x-y 2+1 u(C)=max(0, x-y 2) u(D)=x-y 2+1 u(E)=u(F)=0 u(A)>=u(B)>u(C)>=u(D)>=u(B) Need some invariants, i. e. , y 2<=x/y 3>0 at points B and D, and y 3>0 at point C. start A (y 1, y 2, y 3)=(0, 0, 1) B y 2=y 2+y 3 false D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt
 Uiowa irb
Uiowa irb Intramural iowa state
Intramural iowa state Teori perilaku studi universitas ohio
Teori perilaku studi universitas ohio Iowa state accounts receivable office
Iowa state accounts receivable office University of iowa hospital and clinics departments
University of iowa hospital and clinics departments Sona iowa state
Sona iowa state Iowa mock trial
Iowa mock trial University of iowa college of dentistry
University of iowa college of dentistry University of iowa math department
University of iowa math department University of iowa hawkmail
University of iowa hawkmail Nnpj-296
Nnpj-296 Wac 296-307
Wac 296-307 Wac 296 305
Wac 296 305 Wac 296.305
Wac 296.305 Sos mihai bravu 296
Sos mihai bravu 296 Cs 296
Cs 296 Wac 296-800-160
Wac 296-800-160 E 296
E 296 Wac 296-305
Wac 296-305 When placing solid web members for beams/columns
When placing solid web members for beams/columns Lp html
Lp html Sơ đồ cơ thể người
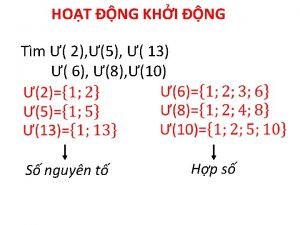
Sơ đồ cơ thể người Số nguyên tố là gì
Số nguyên tố là gì đặc điểm cơ thể của người tối cổ
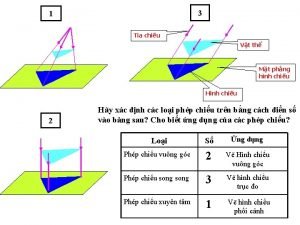
đặc điểm cơ thể của người tối cổ Phối cảnh
Phối cảnh Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thang điểm glasgow
Thang điểm glasgow ưu thế lai là gì
ưu thế lai là gì Tư thế ngồi viết
Tư thế ngồi viết Cái miệng bé xinh thế chỉ nói điều hay thôi
Cái miệng bé xinh thế chỉ nói điều hay thôi Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 Bổ thể
Bổ thể Tư thế ngồi viết
Tư thế ngồi viết V cc cc
V cc cc Thẻ vin
Thẻ vin Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Bài hát chúa yêu trần thế alleluia
Bài hát chúa yêu trần thế alleluia Sự nuôi và dạy con của hươu
Sự nuôi và dạy con của hươu Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Diễn thế sinh thái là
Diễn thế sinh thái là Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Làm thế nào để 102-1=99
Làm thế nào để 102-1=99 Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Lời thề hippocrates
Lời thề hippocrates Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể đại từ thay thế
đại từ thay thế Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Môn thể thao bắt đầu bằng từ chạy
Môn thể thao bắt đầu bằng từ chạy Công thức tính độ biến thiên đông lượng
Công thức tính độ biến thiên đông lượng Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Sự nuôi và dạy con của hươu
Sự nuôi và dạy con của hươu Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Dot
Dot