The University of Iowa 22 c 296 Automated

The University of Iowa 22 c: 296 Automated Software Verification Specification Formalisms Copyright 2003 -04, Doron Peled and Cesare Tinelli. These notes are based on a set of lecture notes originally developed by Doron Peled at the University of Warwick. These notes are copyrighted materials and may not be used in other course settings outside of the University of Iowa in their current form or modified form without the express written permission of the copyright holders. During this course, students are prohibited from selling notes to or being paid for taking notes by any person or commercial firm without the express written permission of the copyright holders.

Properties of formalisms n n Formal. Unique interpretation. Intuitive. Simple to understand (visual). Succinct. Spec. of reasonable size. Effective. n n Check that there are no contradictions. Check that the spec. is implementable. Check that the implementation satisfies spec. Expressive. May be used to generate initial code. Specifying the implementation or its properties? n

A transition system n n n A (finite) set of variables V. A set of states . A (finite) set of transitions T, each transition e==>t has n an enabling condition e and a transformation t. An initial condition I. Denote by R(s, s’) the fact that s’ is a successor of s.

The interleaving model n n An execution is a finite or infinite sequence of states s 0, s 1, s 2 , … The initial state satisfies the initial condition, I. e. , I (s 0). Moving from one state si to si+1 is by executing a transition e==>t: n e(si), I. e. , si satisfies e. n si+1 is obtained by applying t to si. Lets assume all sequences are infinite by extending finite ones by “stuttering” the last state.

Temporal logic n n Dynamic, speaks about several “worlds” and the relation between them. Our “worlds” are the states in an execution. There is a linear relation between them, each two sequences in our execution are ordered. Interpretation: over an execution, later over all executions.

LTL: Syntax : : = ( ) | ¬ | / / U |O | p “box”, “always”, “forever” “diamond”, “eventually”, “sometimes” O “nexttime” U “until” Propositions p, q, r, … Each represents some state property (x>y+1, z=t, at-CR, etc. )

Semantics O U

Combinations n n n []<>p “p will happen infinitely often” <>[]p “p will happen from some point forever”. ([]<>p) --> ([]<>q) “If p happens infinitely often, then q also happens infinitely often”.

Some relations: n n [](a/b)=([]a)/([]b) But <>(a/b) (<>a)/(<>b) b n n a <>(a/b)=(<>a)/(<>b) But [](a/b) ([]a)/([]b) b a b a b a

Can discard some operators n n Instead of <>p, write true U p. Instead of []p, we can write ¬<>¬p, or ¬(true U ¬p). Because []p=¬¬[]p means it is not true that p holds forever, or at some point ¬p holds or <>¬p.

Formal semantic definition n n n n Let be a sequence 0 1 2 … Let i be a suffix of i i+1 i+2 … |= p, where p a proposition, if 0 |=p. |= / if |= and |= / if |= or |= <> if for some i 0, i |= [] if for each i 0, i |= U if for some i 0, i |=. and for each 0 j<i, j |=.

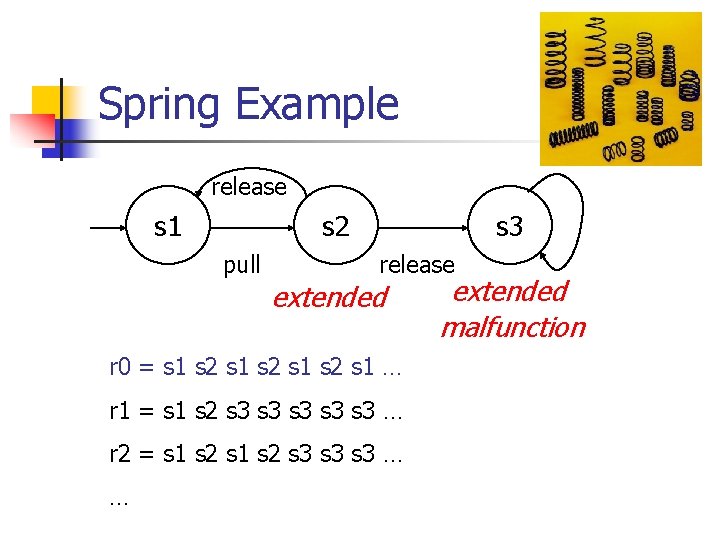
Spring Example release s 1 s 2 pull s 3 release extended r 0 = s 1 s 2 s 1 … r 1 = s 1 s 2 s 3 s 3 s 3 … r 2 = s 1 s 2 s 3 s 3 … … extended malfunction

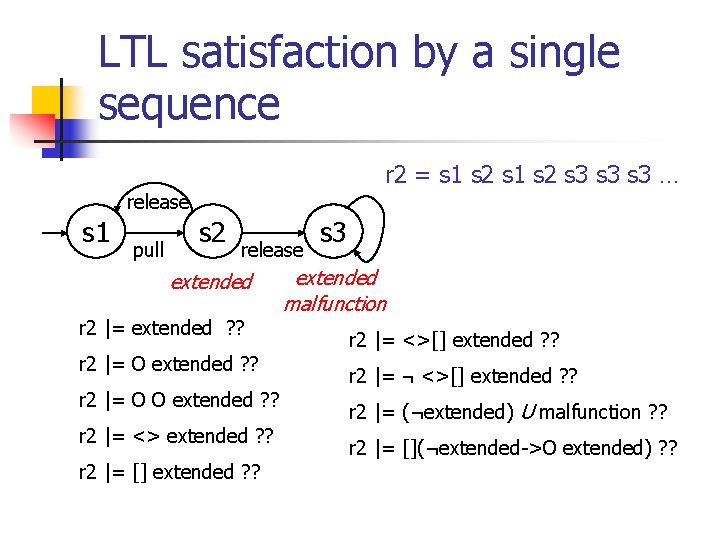
LTL satisfaction by a single sequence r 2 = s 1 s 2 s 3 s 3 … release s 1 pull s 2 release extended r 2 |= extended ? ? r 2 |= O O extended ? ? r 2 |= <> extended ? ? r 2 |= [] extended ? ? s 3 extended malfunction r 2 |= <>[] extended ? ? r 2 |= ¬ <>[] extended ? ? r 2 |= (¬extended) U malfunction ? ? r 2 |= [](¬extended->O extended) ? ?

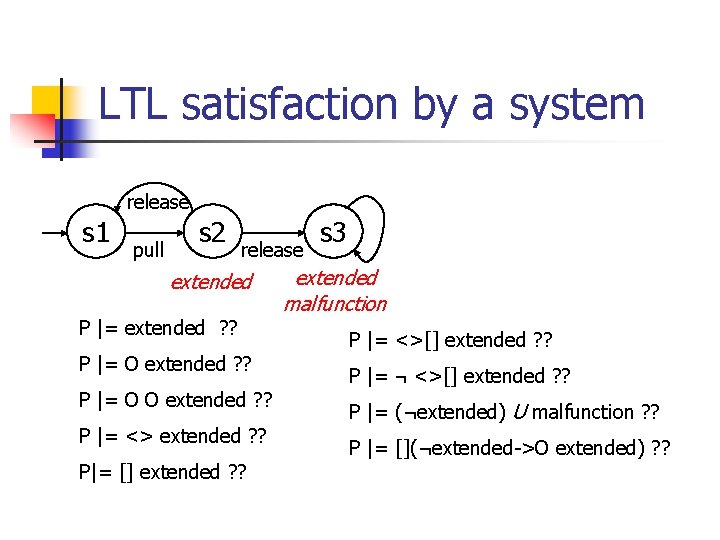
LTL satisfaction by a system release s 1 pull s 2 release extended P |= extended ? ? P |= O O extended ? ? P |= <> extended ? ? P|= [] extended ? ? s 3 extended malfunction P |= <>[] extended ? ? P |= ¬ <>[] extended ? ? P |= (¬extended) U malfunction ? ? P |= [](¬extended->O extended) ? ?

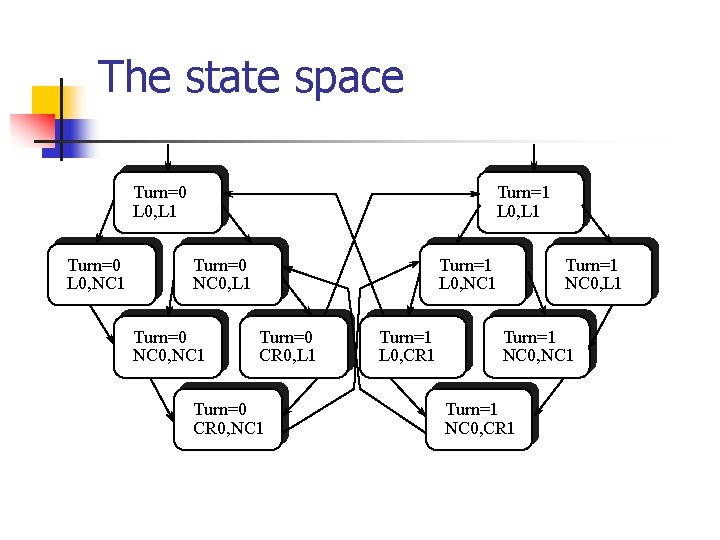
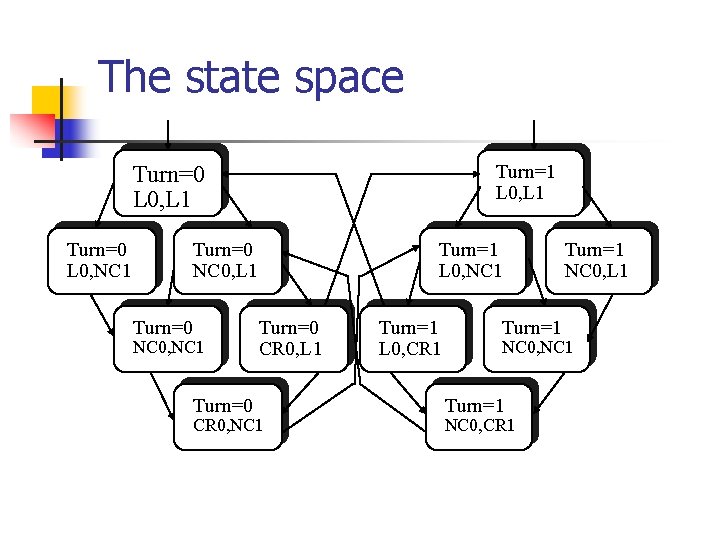
The state space Turn=1 L 0, L 1 Turn=0 L 0, NC 1 Turn=0 NC 0, L 1 Turn=0 NC 0, NC 1 Turn=1 L 0, NC 1 Turn=0 CR 0, L 1 Turn=0 CR 0, NC 1 Turn=1 L 0, CR 1 Turn=1 NC 0, L 1 Turn=1 NC 0, NC 1 Turn=1 NC 0, CR 1

[]¬)PC 0=CR 0/PC 1=CR 1) (Mutual exclusion) Turn=0 L 0, L 1 Turn=0 L 0, NC 1 Turn=1 L 0, L 1 Turn=0 NC 0, NC 1 Turn=1 L 0, NC 1 Turn=0 CR 0, L 1 Turn=0 CR 0, NC 1 Turn=1 L 0, CR 1 Turn=1 NC 0, L 1 Turn=1 NC 0, NC 1 Turn=1 NC 0, CR 1

[](Turn=0 --> <>Turn=1) Turn=0 L 0, L 1 Turn=0 L 0, NC 1 Turn=1 L 0, L 1 Turn=0 NC 0, NC 1 Turn=1 L 0, NC 1 Turn=0 CR 0, L 1 Turn=0 CR 0, NC 1 Turn=1 L 0, CR 1 Turn=1 NC 0, L 1 Turn=1 NC 0, NC 1 Turn=1 NC 0, CR 1

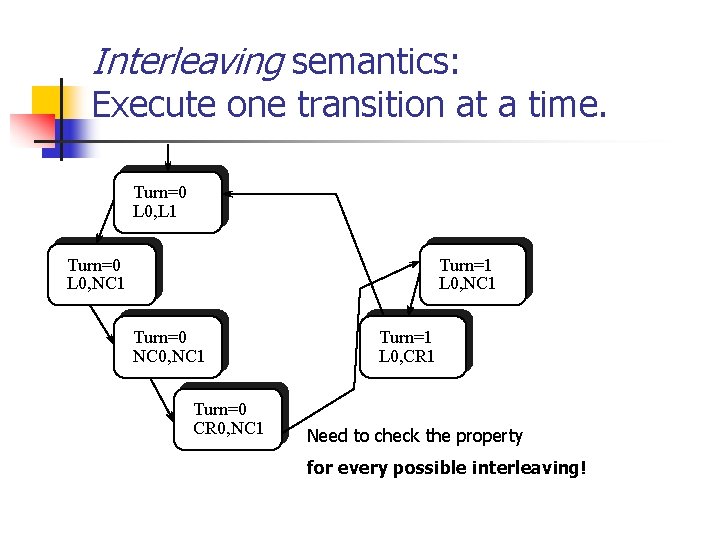
Interleaving semantics: Execute one transition at a time. Turn=0 L 0, L 1 Turn=0 L 0, NC 1 Turn=1 L 0, NC 1 Turn=0 NC 0, NC 1 Turn=0 CR 0, NC 1 Turn=1 L 0, CR 1 Need to check the property for every possible interleaving!

More specifications n n n [](PC 0=NC 0 --> <> PC 0=CR 0) [](PC 0=NC 0 U Turn=0) Try at home: - The processes alternate in entering their critical sections. - Each process enters its critical section infinitely often.

Proof system n n n n ¬<>p<-->[]¬p [](p-->q)-->([]p-->[]q) []p-->(p/O[]p) O¬p<-->¬Op [](p-->Op)-->(p-->[]p) (p. Uq)<-->(q/(p/O(p. Uq))) (p. Uq)--><>q n n + propositional logic axioms + proof rules: p p->q -----q |- p ------|- []p

Traffic light example Green --> Yellow --> Red --> Green Always has exactly one light: [](¬(gr/ye)/¬(ye/re)/¬(re/gr)/(gr/ye/re)) Correct change of color: []((gr. Uye)/(ye. Ure)/(re. Ugr))

Another kind of traffic light Green-->Yellow-->Red-->Yellow-->Green First attempt: [](((gr/re) U ye)/(ye U (gr/re))) Correct specification: []( (gr-->(gr U (ye / ( ye U re )))) /(re-->(re U (ye / ( ye U gr )))) /(ye-->(ye U (gr / re)))) Needed only when we can start with yellow

Properties of sequential programs n n n init-when the program starts and satisfies the initial condition. finish-when the program terminates and nothing is enabled. Partial correctness: init/[](finish--> ) Termination: init/<>finish Total correctness: init/<>(finish/ ) Invariant: init/[]

Some fairness definitions n Strong transition fairness: n Weak transition fairness: en. Pi some transition of process Pi is enabled. n Strong process fairness: en. Pi = / Pi en n Weak process fairness: exec is executed. exec. Pi some transition of Pi is executed. en is enabled. exec. Pi = / Pi exec / T ([]<>en -->[]<>exec ) / T (<>[]en -->[]<>exec ). /Pi ([]<>en. Pi -->[]<>exec. Pi ) /Pi (<>[]en. Pi -->[]<>exec. Pi )

Finite State Automata

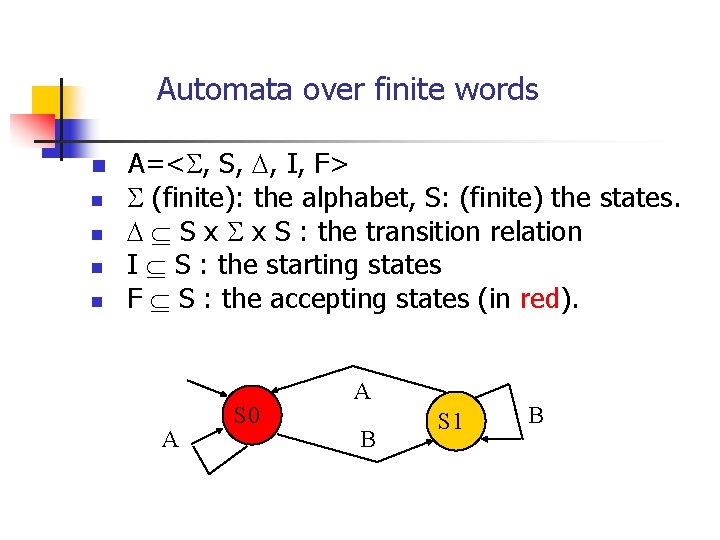
Automata over finite words n n n A=< , S, , I, F> (finite): the alphabet, S: (finite) the states. S x x S : the transition relation I S : the starting states F S : the accepting states (in red). A S 0 A B S 1 B

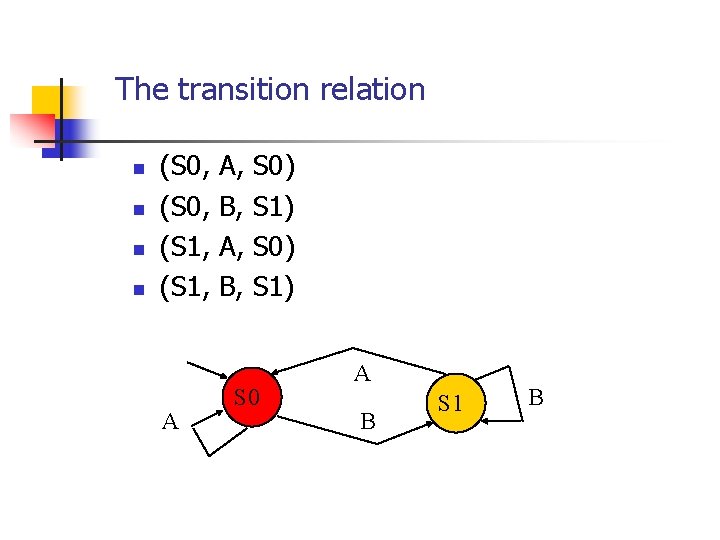
The transition relation n n (S 0, (S 1, A A, B, S 0) S 1) S 0 A B S 1 B

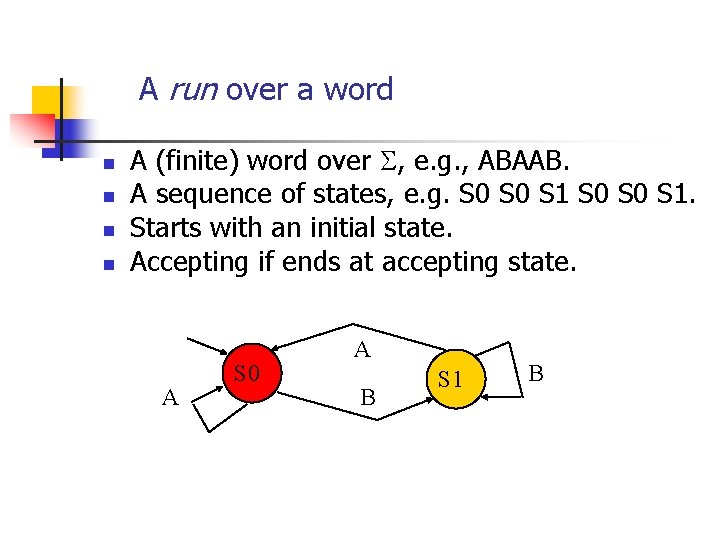
A run over a word n n A (finite) word over , e. g. , ABAAB. A sequence of states, e. g. S 0 S 0 S 1. Starts with an initial state. Accepting if ends at accepting state. A S 0 A B S 1 B

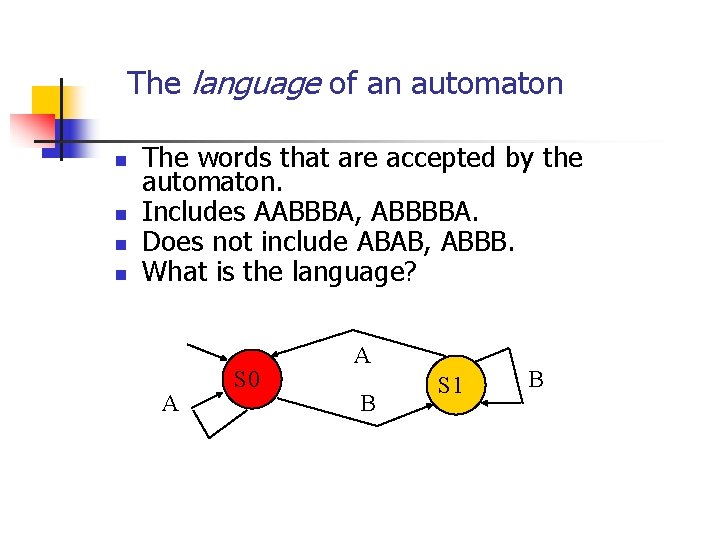
The language of an automaton n n The words that are accepted by the automaton. Includes AABBBA, ABBBBA. Does not include ABAB, ABBB. What is the language? A S 0 A B S 1 B

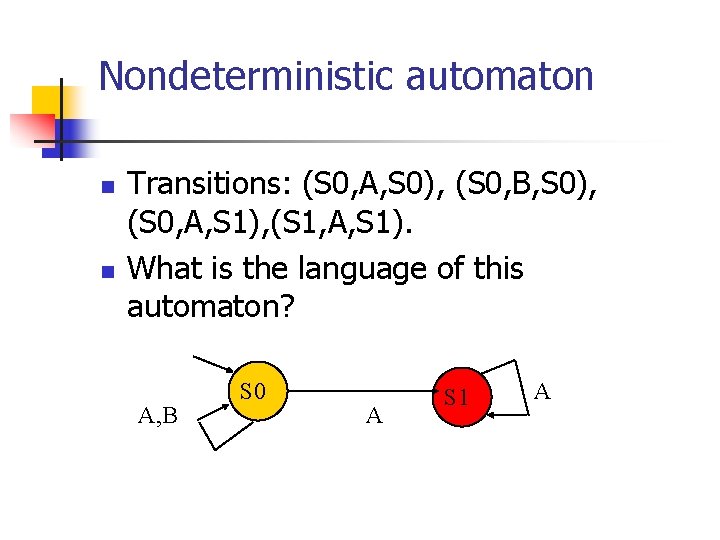
Nondeterministic automaton n n Transitions: (S 0, A, S 0), (S 0, B, S 0), (S 0, A, S 1), (S 1, A, S 1). What is the language of this automaton? A, B S 0 A S 1 A

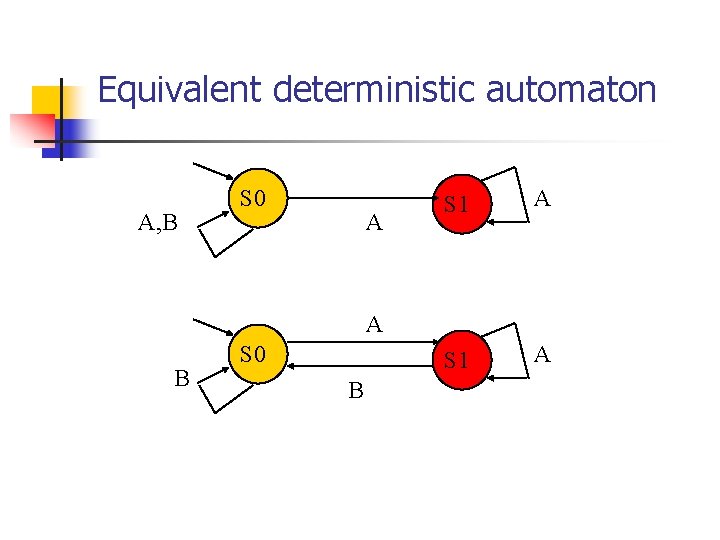
Equivalent deterministic automaton A, B S 0 A S 1 A A B S 0 B

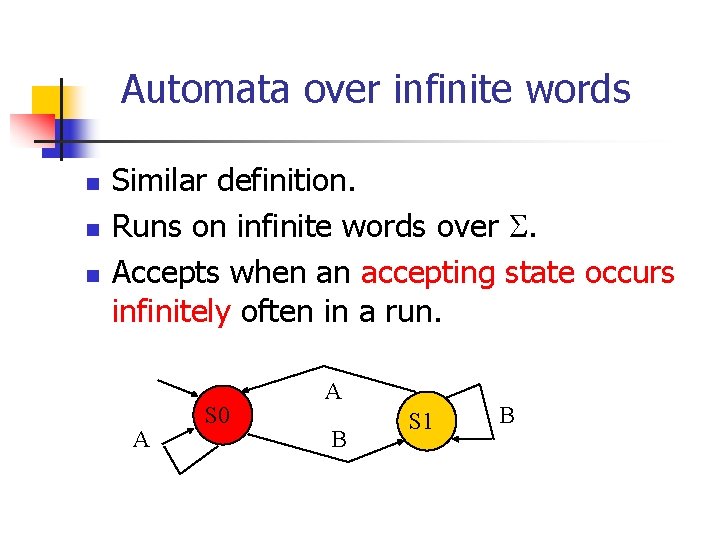
Automata over infinite words n n n Similar definition. Runs on infinite words over . Accepts when an accepting state occurs infinitely often in a run. A S 0 A B S 1 B

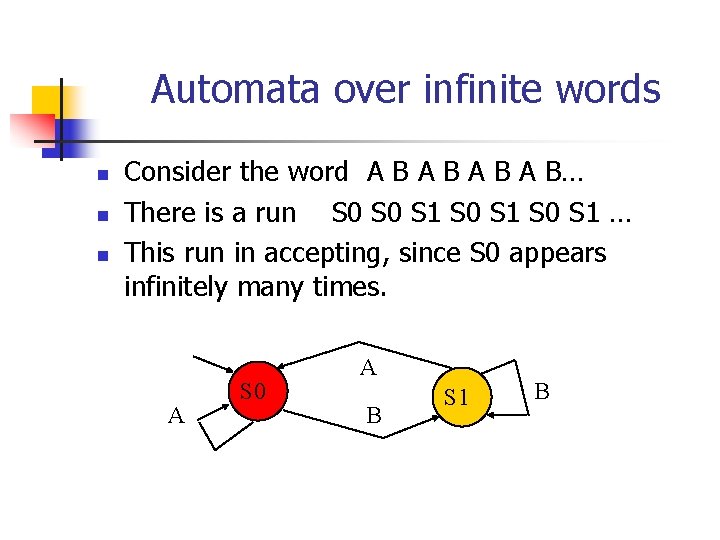
Automata over infinite words n n n Consider the word A B A B… There is a run S 0 S 1 … This run in accepting, since S 0 appears infinitely many times. A S 0 A B S 1 B

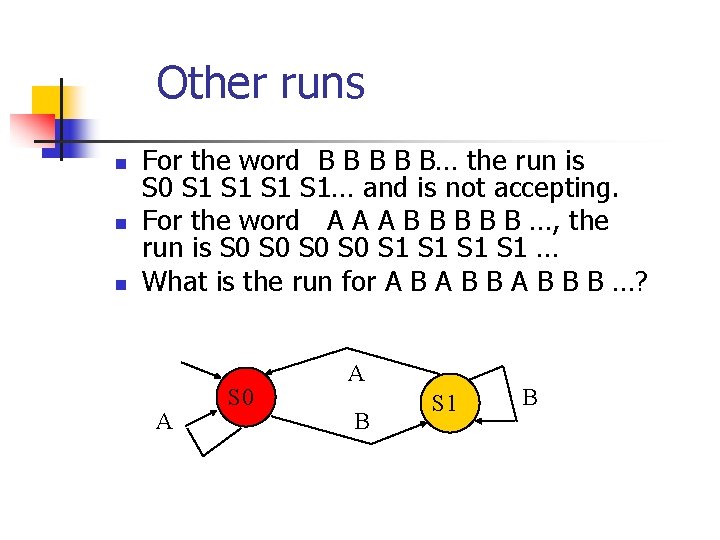
Other runs n n n For the word B B B… the run is S 0 S 1 S 1… and is not accepting. For the word A A A B B B …, the run is S 0 S 0 S 1 S 1 … What is the run for A B B B …? A S 0 A B S 1 B

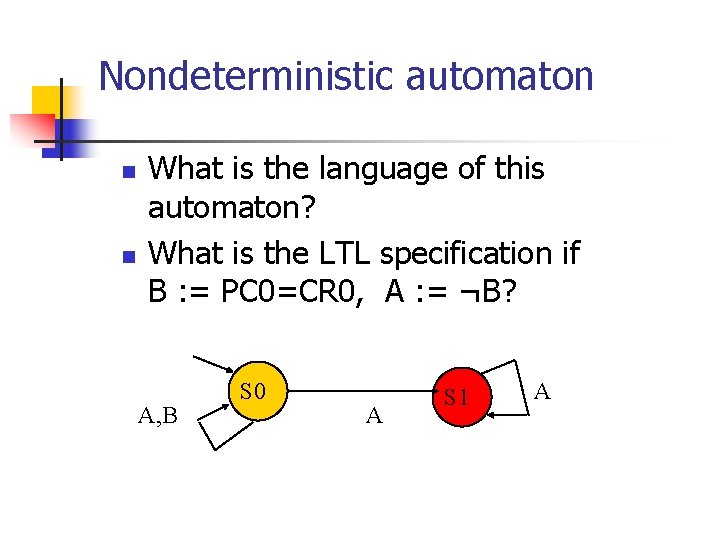
Nondeterministic automaton n n What is the language of this automaton? What is the LTL specification if B : = PC 0=CR 0, A : = ¬B? A, B S 0 A S 1 A

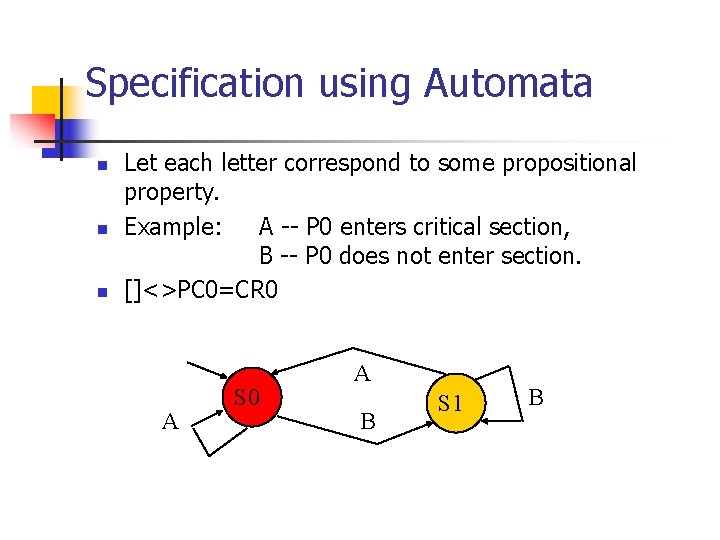
Specification using Automata n n n Let each letter correspond to some propositional property. Example: A -- P 0 enters critical section, B -- P 0 does not enter section. []<>PC 0=CR 0 A S 0 A B S 1 B

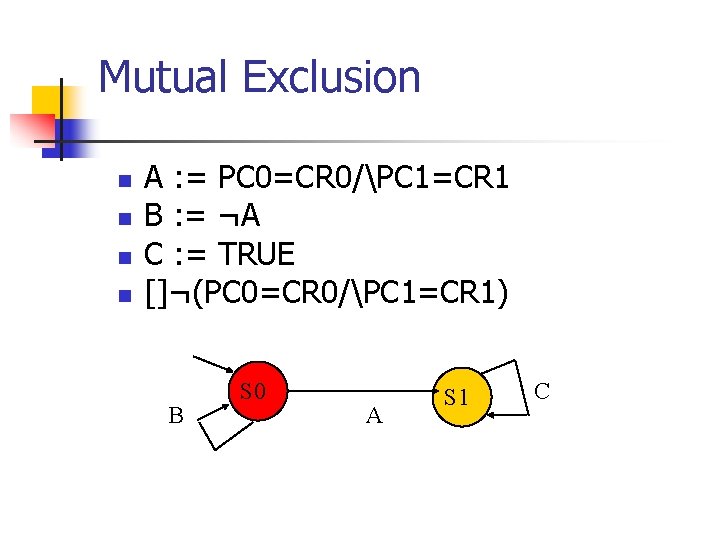
Mutual Exclusion n n A : = PC 0=CR 0/PC 1=CR 1 B : = ¬A C : = TRUE []¬(PC 0=CR 0/PC 1=CR 1) B S 0 A S 1 C

L 0: While True do NC 0: wait(Turn=0); CR 0: Turn=1 endwhile || L 1: While True do NC 1: wait(Turn=1); CR 1: Turn=0 endwhile T 0: PC 0=L 0==>PC 0=NC 0 T 1: PC 0=NC 0/Turn=0==> PC 0: =CR 0 T 2: PC 0=CR 0==> (PC 0, Turn): =(L 0, 1) T 3: PC 1==L 1==>PC 1=NC 1 T 4: PC 1=NC 1/Turn=1==> PC 1: =CR 1 T 5: PC 1=CR 1==> (PC 1, Turn): =(L 1, 0) Initially: PC 0=L 0/PC 1=L 1

The state space Turn=1 L 0, L 1 Turn=0 L 0, NC 1 Turn=0 NC 0, L 1 Turn=0 NC 0, NC 1 Turn=0 Turn=1 L 0, NC 1 Turn=0 CR 0, L 1 CR 0, NC 1 Turn=1 L 0, CR 1 Turn=1 NC 0, L 1 NC 0, NC 1 Turn=1 NC 0, CR 1

[]¬)PC 0=CR 0/PC 1=CR 1) Turn=1 L 0, L 1 Turn=0 L 0, NC 1 Turn=0 NC 0, L 1 Turn=0 NC 0, NC 1 Turn=0 Turn=1 L 0, NC 1 Turn=0 CR 0, L 1 CR 0, NC 1 Turn=1 L 0, CR 1 Turn=1 NC 0, L 1 NC 0, NC 1 Turn=1 NC 0, CR 1

)[]Turn=0 --> <>Turn=1) Turn=1 L 0, L 1 Turn=0 L 0, NC 1 Turn=0 NC 0, L 1 Turn=0 NC 0, NC 1 Turn=0 Turn=1 L 0, NC 1 Turn=0 CR 0, L 1 CR 0, NC 1 Turn=1 L 0, CR 1 Turn=1 NC 0, L 1 NC 0, NC 1 Turn=1 NC 0, CR 1

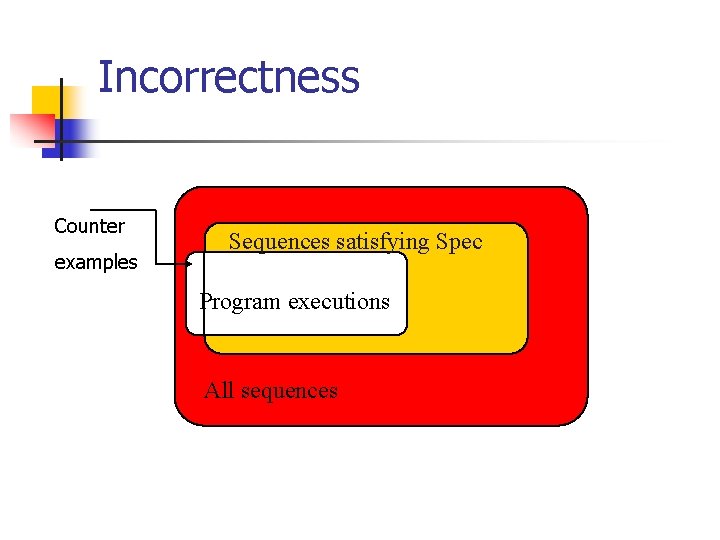
Correctness condition n We want to find a correctness condition for a model to satisfy a specification. Language of a model: L(Model) Language of a specification: L(Spec). n We need: L(Model) L(Spec). n n

Correctness Sequences satisfying Spec Program executions All sequences

Incorrectness Counter examples Sequences satisfying Spec Program executions All sequences