The Peak Effect Gautam I Menon IMSc Chennai


























- Slides: 56

The Peak Effect Gautam I. Menon IMSc, Chennai, India 1

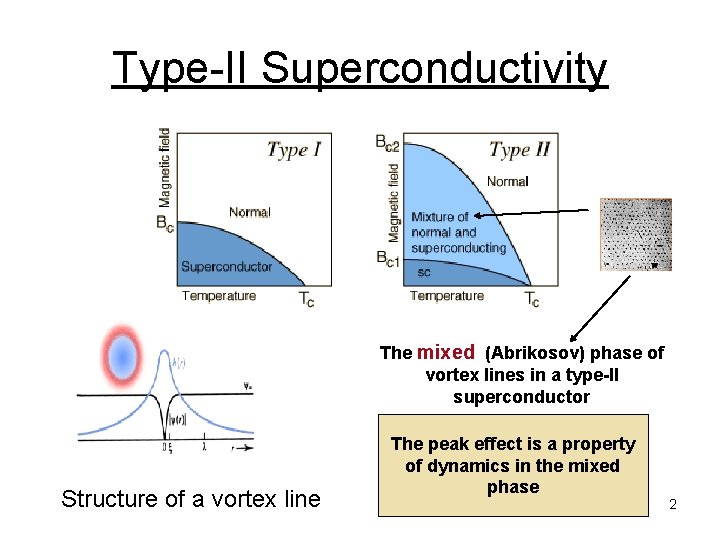
Type-II Superconductivity The mixed (Abrikosov) phase of vortex lines in a type-II superconductor Structure of a vortex line The peak effect is a property of dynamics in the mixed phase 2

How are forces exerted on vortex lines? How do vortex lines move under the action of an external force? 3

Lorentz Force on Flux Lines Force/unit volume Local supercurrent density Magnetic pressure Local induction Tension along lines of force 4

Dissipation from Line Motion Viscous forces oppose motion, damping coefficient g, lines move with velocity v Competition of applied and viscous forces yields a steady state, motion of vortices produces an electric field Power dissipation from EJ, thus nonzero resistivity from flux flow 5

Random Pinning Forces • To prevent dissipation, pin lines by quenched random disorder • Line feels sum of many random forces • Summation problem: Adding effects of these random forces. How does quenched randomness affect the crystal? 6

Elasticity and Pinning compete In the experimental situation, a random potential from pinning sites The lattice deforms to accommodate to the pinning, but pays elastic energy Pinning always wins at the largest length scales: no translational long-range order (Larkin) 7

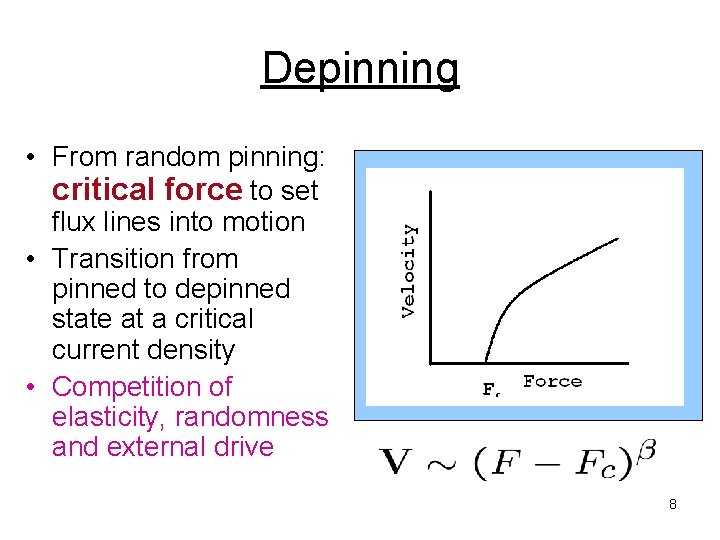
Depinning • From random pinning: critical force to set flux lines into motion • Transition from pinned to depinned state at a critical current density • Competition of elasticity, randomness and external drive 8

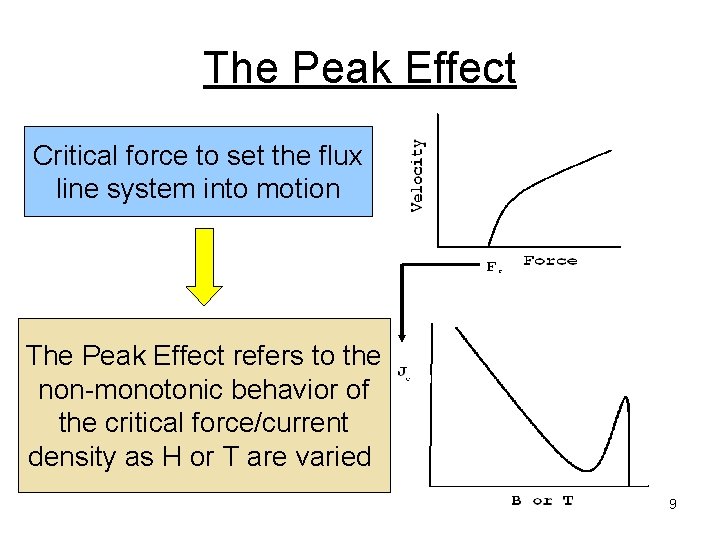
The Peak Effect Critical force to set the flux line system into motion The Peak Effect refers to the non-monotonic behavior of the critical force/current density as H or T are varied 9

How is this critical force computed? 10

Larkin Lengths • At large scales, disorder induced relative displacements of the lattice increase • Define Larkin lengths 11

Estimating Jc Pinning induces Larkin domains. External drive balances gain from domain formation. collective pinning theory Larkin and Ovchinnikov J. Low Temp. Phys 34 409 (1979) Role of the Larkin lengths/Larkin Volume 12

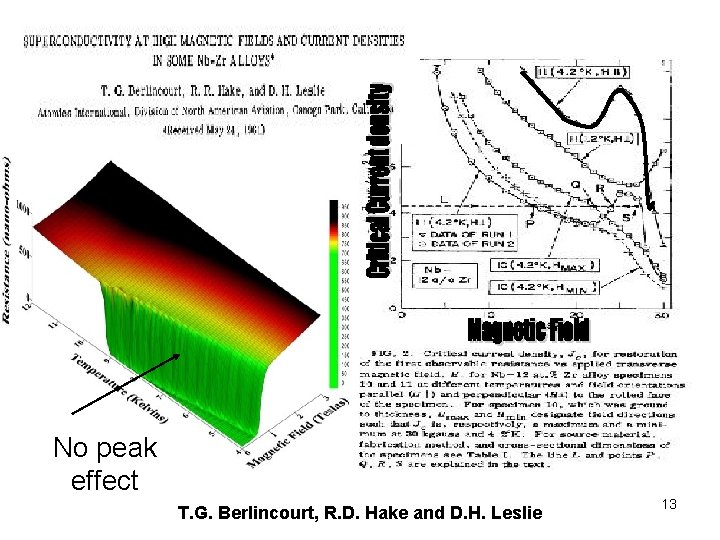
No peak effect T. G. Berlincourt, R. D. Hake and D. H. Leslie 13

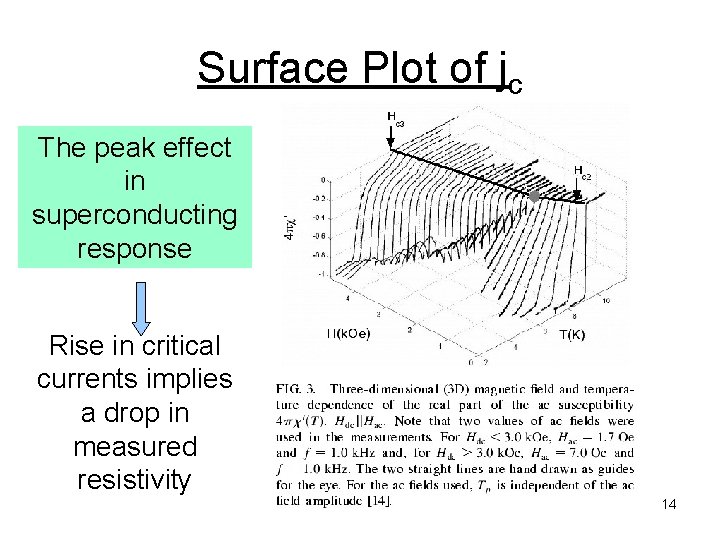
Surface Plot of jc The peak effect in superconducting response Rise in critical currents implies a drop in measured resistivity 14

Why does the peak effect occur? Many explanations … 15

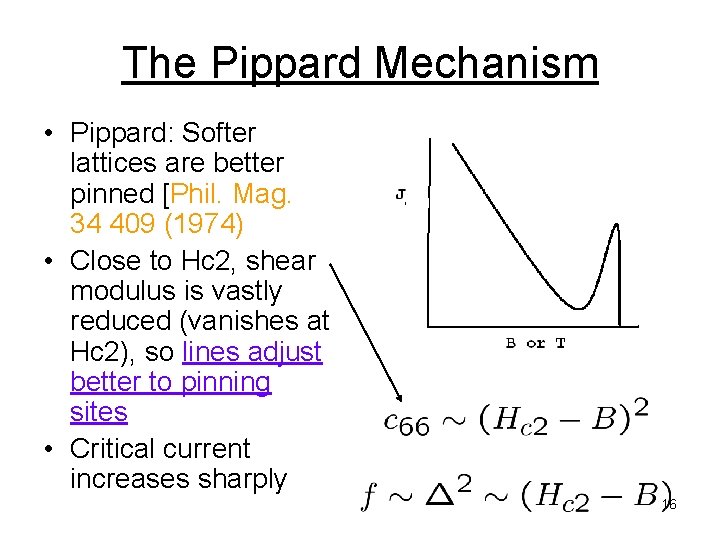
The Pippard Mechanism • Pippard: Softer lattices are better pinned [Phil. Mag. 34 409 (1974) • Close to Hc 2, shear modulus is vastly reduced (vanishes at Hc 2), so lines adjust better to pinning sites • Critical current increases sharply 16

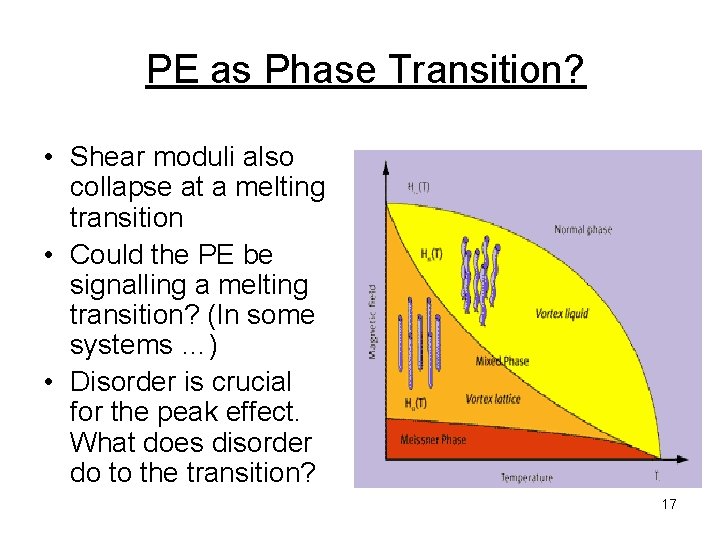
PE as Phase Transition? • Shear moduli also collapse at a melting transition • Could the PE be signalling a melting transition? (In some systems …) • Disorder is crucial for the peak effect. What does disorder do to the transition? 17

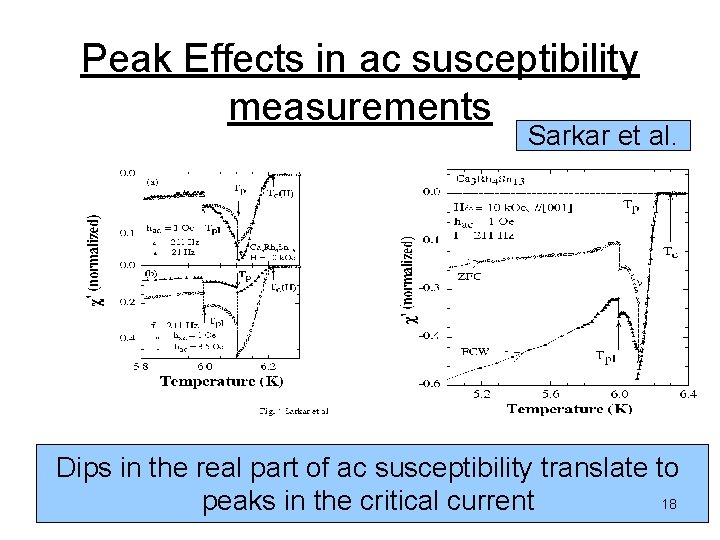
Peak Effects in ac susceptibility measurements Sarkar et al. Dips in the real part of ac susceptibility translate to 18 peaks in the critical current

Will concentrate principally on transport measurements G. Ravikumar’s lecture: Magnetization, susceptibility 19

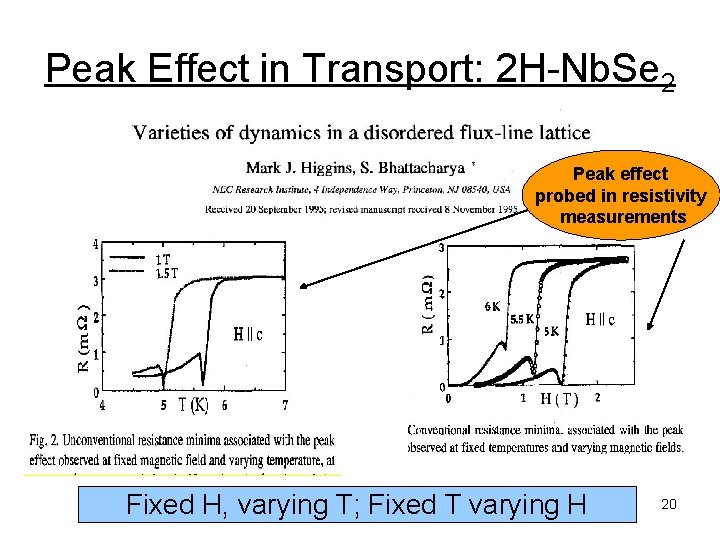
Peak Effect in Transport: 2 H-Nb. Se 2 Peak effect probed in resistivity measurements Fixed H, varying T; Fixed T varying H 20

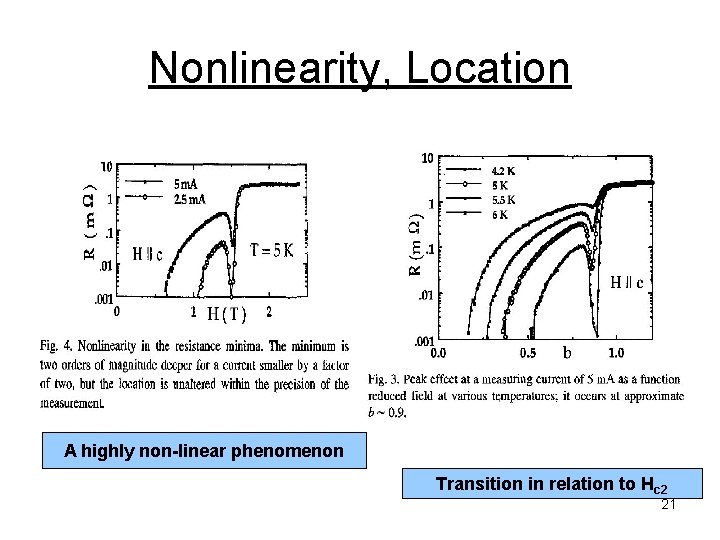
Nonlinearity, Location A highly non-linear phenomenon Transition in relation to Hc 2 21

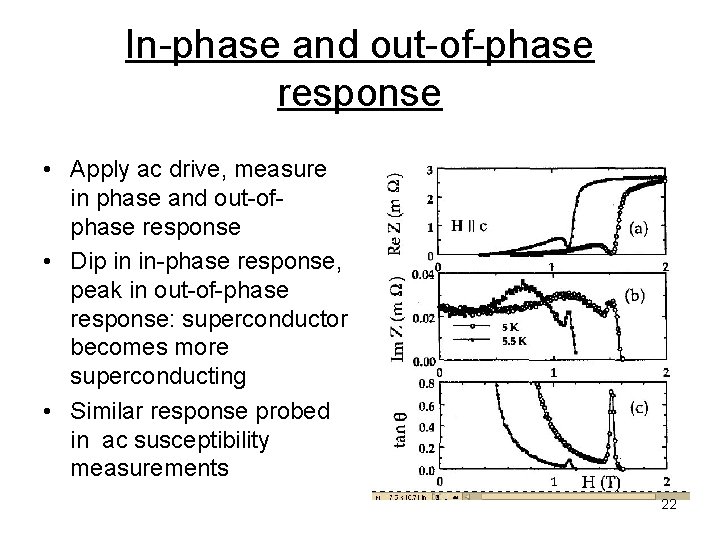
In-phase and out-of-phase response • Apply ac drive, measure in phase and out-ofphase response • Dip in in-phase response, peak in out-of-phase response: superconductor becomes more superconducting • Similar response probed in ac susceptibility measurements 22

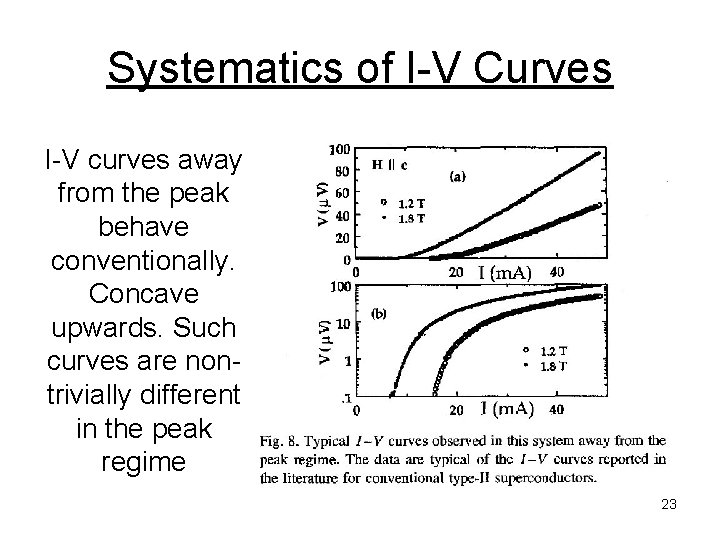
Systematics of I-V Curves I-V curves away from the peak behave conventionally. Concave upwards. Such curves are nontrivially different in the peak regime 23

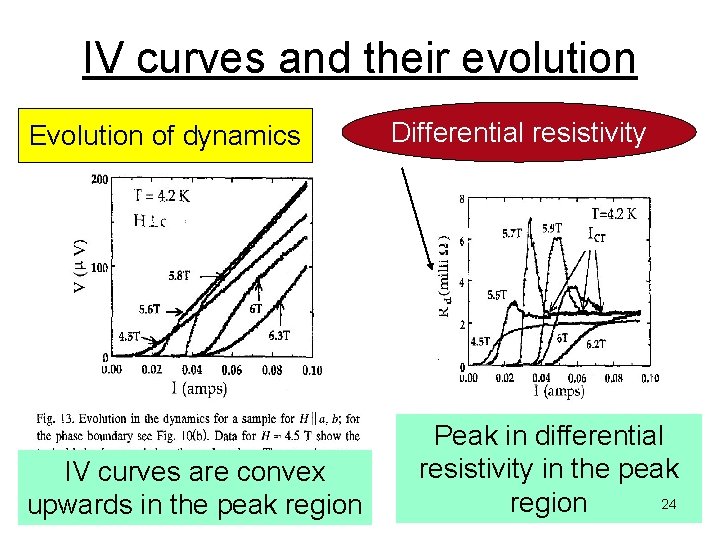
IV curves and their evolution Evolution of dynamics IV curves are convex upwards in the peak region Differential resistivity Peak in differential resistivity in the peak 24 region

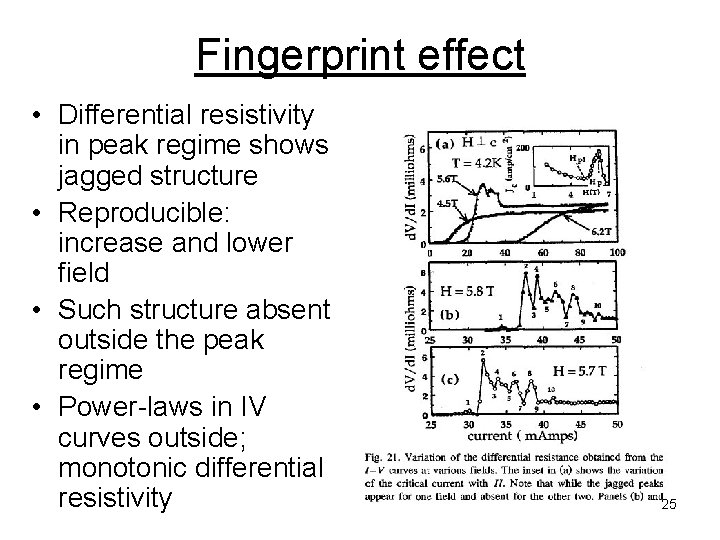
Fingerprint effect • Differential resistivity in peak regime shows jagged structure • Reproducible: increase and lower field • Such structure absent outside the peak regime • Power-laws in IV curves outside; monotonic differential resistivity 25

Interpretation of Fingerprints? • A “Fingerprint” of the structure of disorder? • Depinning of the flux-line lattice proceeds via a series of specific and reproducible near-jumps in I-V curves • This type of finger print is the generic outcome of the breaking up of the fluxline lattice due to plastic flow in a regime intermediate between elastic and fluid flow (Higgins and Bhattacharya) 26

Noise • If plastic flow is key, flow should be noisy • Measure frequency dependence of differential resistivity in the peak region • Yes: Anomalously slow dynamics is associated with plastic flow. Occurs at small velocities and heals at large velocities where the lattice becomes more correlated. • A velocity correlation length Lv 27

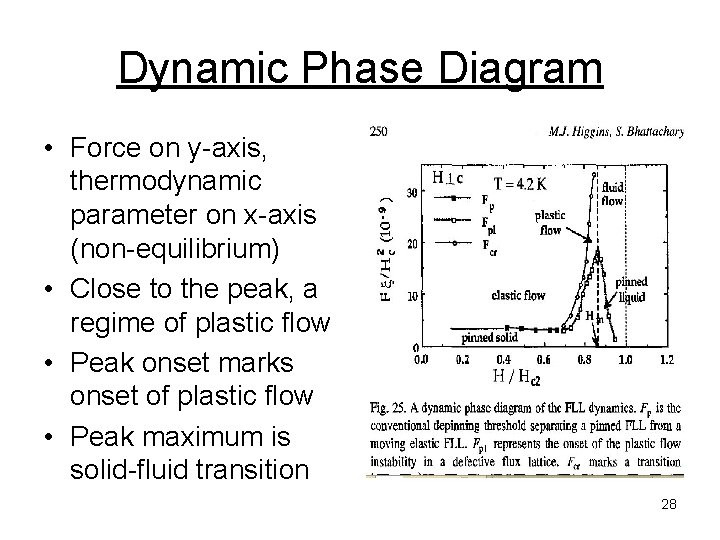
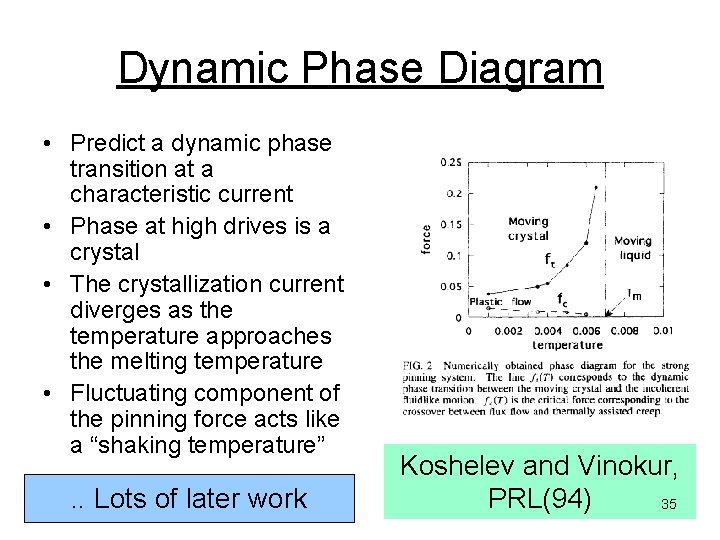
Dynamic Phase Diagram • Force on y-axis, thermodynamic parameter on x-axis (non-equilibrium) • Close to the peak, a regime of plastic flow • Peak onset marks onset of plastic flow • Peak maximum is solid-fluid transition 28

Numerical Simulations • Brandt, Jensen, Berlinsky, Shi, Brass. . • Koshelev, Vinokur • Faleski, Marchetti, Middleton • Nori, Reichhardt, Olson • Scalettar, Zimanyi, Chandran. . And a whole lot more … 29

Simulations: The General Idea • • • Interaction – soft (numerically easy) or realistic Disorder, typically large number of weak pinning sites, but also correlated disorder Apply forces, overdamped eqn of motion, measure response Depinning thresholds, top defects, diff resistivity, healing defects through motion, Equilibrium aspects: the phase diagram 30

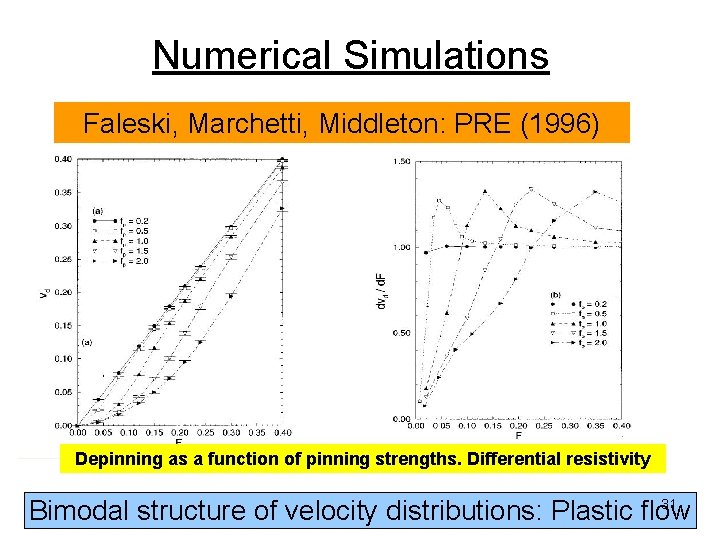
Numerical Simulations Faleski, Marchetti, Middleton: PRE (1996) Depinning as a function of pinning strengths. Differential resistivity 31 Bimodal structure of velocity distributions: Plastic flow

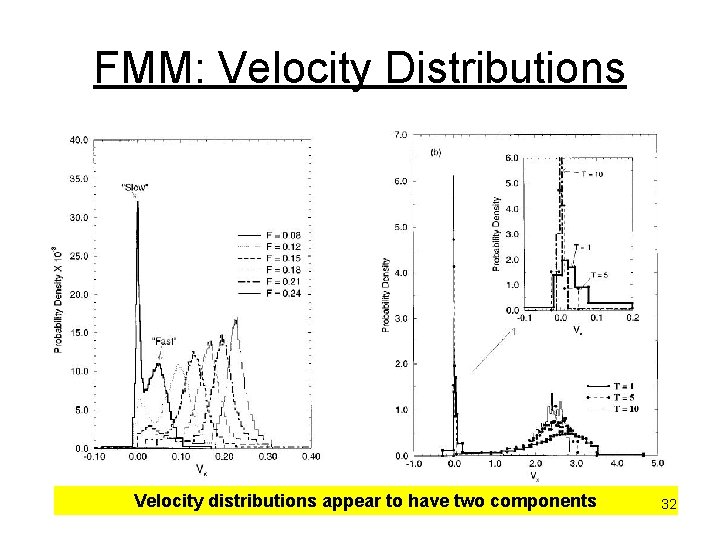
FMM: Velocity Distributions Velocity distributions appear to have two components 32

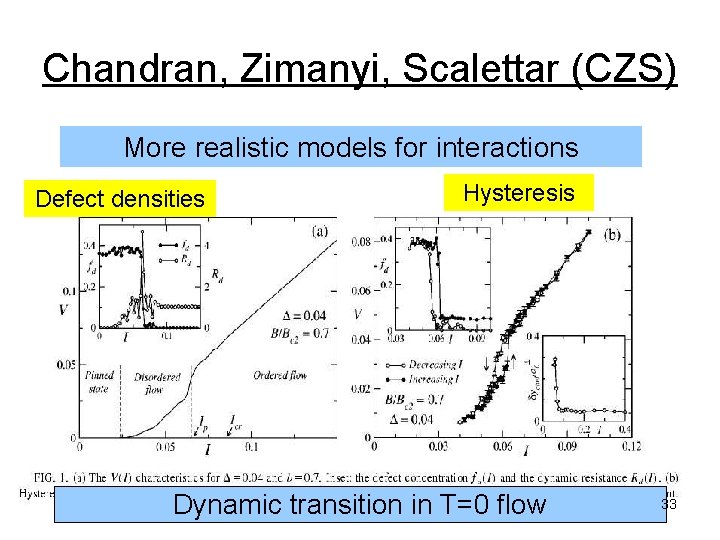
Chandran, Zimanyi, Scalettar (CZS) More realistic models for interactions Defect densities Hysteresis Dynamic transition in T=0 flow 33

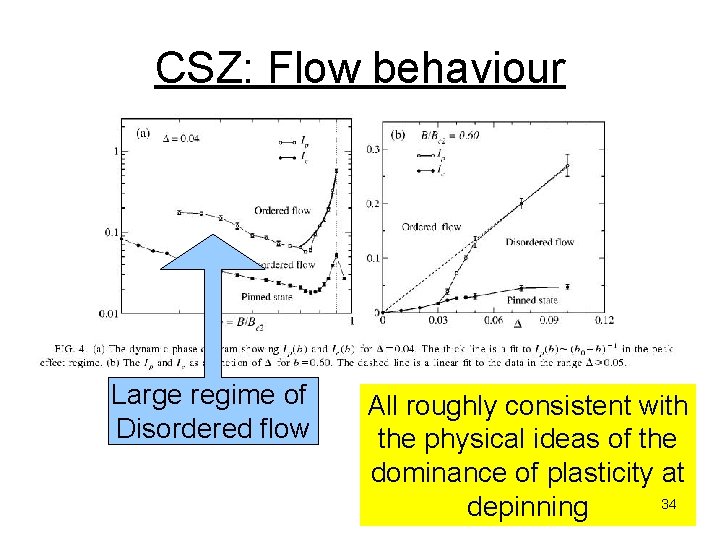
CSZ: Flow behaviour Large regime of Disordered flow All roughly consistent with the physical ideas of the dominance of plasticity at 34 depinning

Dynamic Phase Diagram • Predict a dynamic phase transition at a characteristic current • Phase at high drives is a crystal • The crystallization current diverges as the temperature approaches the melting temperature • Fluctuating component of the pinning force acts like a “shaking temperature” . . Lots of later work Koshelev and Vinokur, PRL(94) 35

Simulations: Summary • We now know a lot more about the depinning behaviour of two-dimensional solids in a quenched disorder background. • Variety of new characterizations from the simulations of plastic flow phenomena • Dynamic phase transitions in disordered systems • Yet. . May not have told us much about the peak effect phenomenon itself 36

Return to the experiments 37

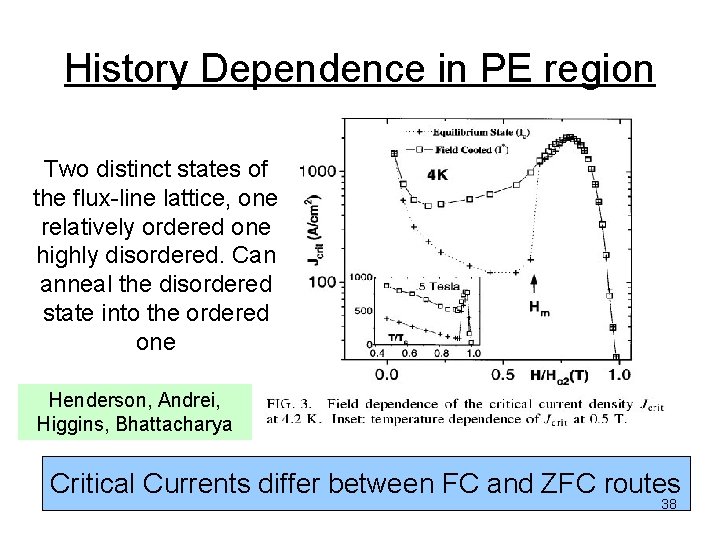
History Dependence in PE region Two distinct states of the flux-line lattice, one relatively ordered one highly disordered. Can anneal the disordered state into the ordered one Henderson, Andrei, Higgins, Bhattacharya Critical Currents differ between FC and ZFC routes 38

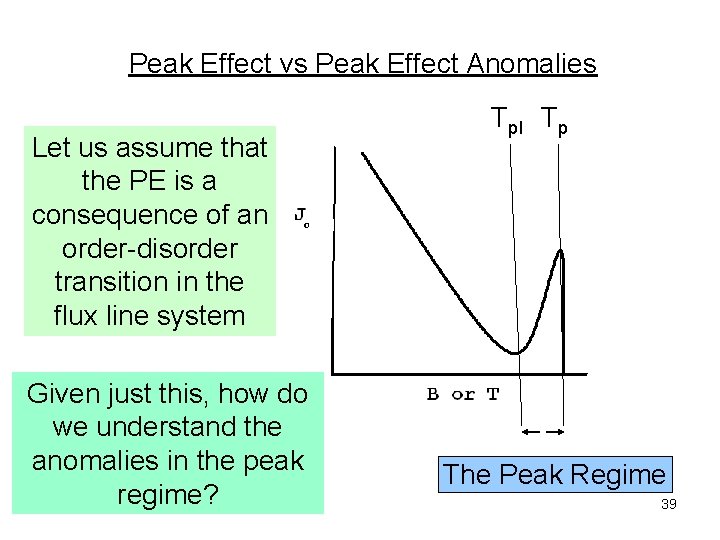
Peak Effect vs Peak Effect Anomalies Let us assume that the PE is a consequence of an order-disorder transition in the flux line system Given just this, how do we understand the anomalies in the peak regime? Tpl Tp The Peak Regime 39

Zeldov and collaborators: Peak Effect anomalies as a consequence of the injection of a meta-stable phase at the sample boundaries and annealing within the bulk Boundaries may play a significant role in PE physics 40

The Effects of Sample Edges • Role of barriers to flux entry and departure at sample surfaces • Bean-Livingston barrier • Currents flow near surface to ensure entry and departure of lines • Significant dissipation from surfaces 41

Corbino geometry: Zeldov and collaborators Surface effects can be eliminated by working in a Corbino geometry. Peak effect sharpens, associated with Hp 42

Relevance of Edges • Both dc and ac drives • Hall probe measurements • Measure critical currents for both ac and dc through lock-in techniques • Intermediate regime of coexistence from edge contamination 43

Direct access to currents • Map current flow using Maxwells equations and measured magnetic induction using the Hall probe method • Most of the current flows at the edges, little at the bulk • Dissipation mostly edge driven? 44

Andrei and collaborators • Start with ZFC state, ramp current up and then down • Different critical current. . • “Jumpy” behavior on first ramp • Lower threshold on subsequent ramps 46

Plastic motion/Alternating Currents • Steady state response to bi-directional pulses vs unidirectional pulses • Motion if bi-directional current even if amplitude is below the dc critical current • No response to unidirectional pulses Henderson, Andrei, Higgins 47

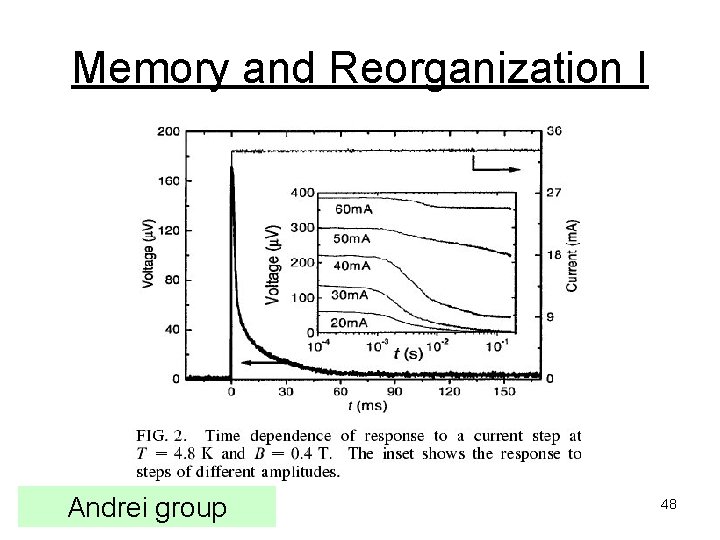
Memory and Reorganization I Andrei group 48

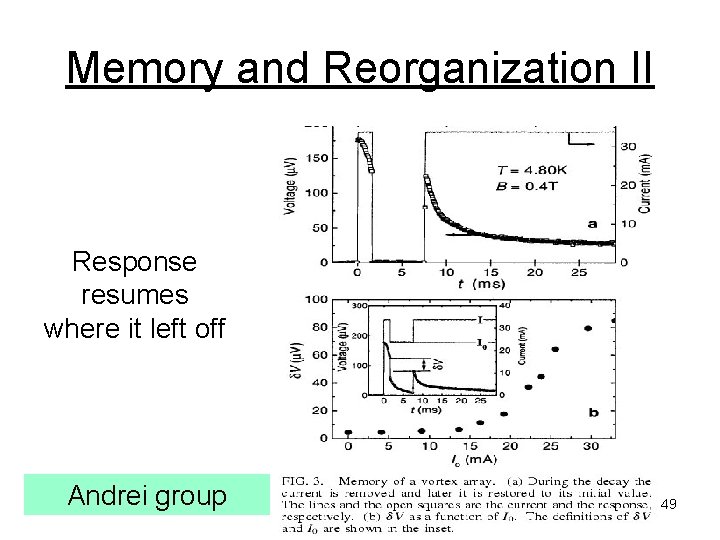
Memory and Reorganization II Response resumes where it left off Andrei group 49

Generalized Dynamic Phase Diagram More complex intermediate “Phases” in a disordered system under flow 50

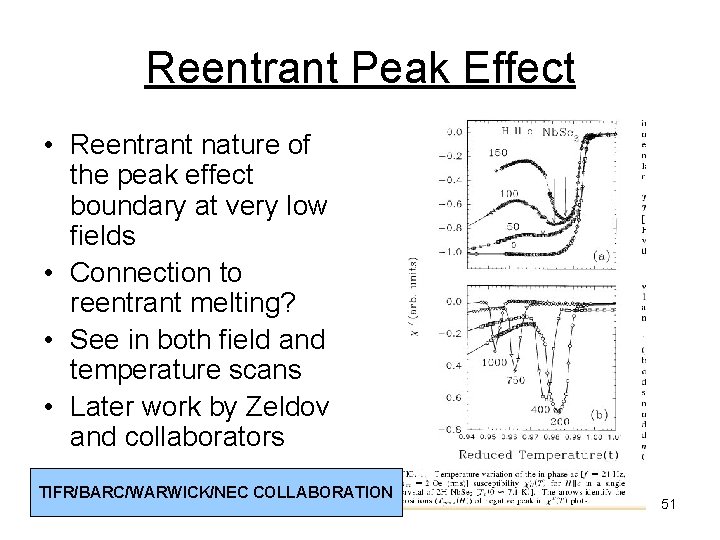
Reentrant Peak Effect • Reentrant nature of the peak effect boundary at very low fields • Connection to reentrant melting? • See in both field and temperature scans • Later work by Zeldov and collaborators TIFR/BARC/WARWICK/NEC COLLABORATION 51

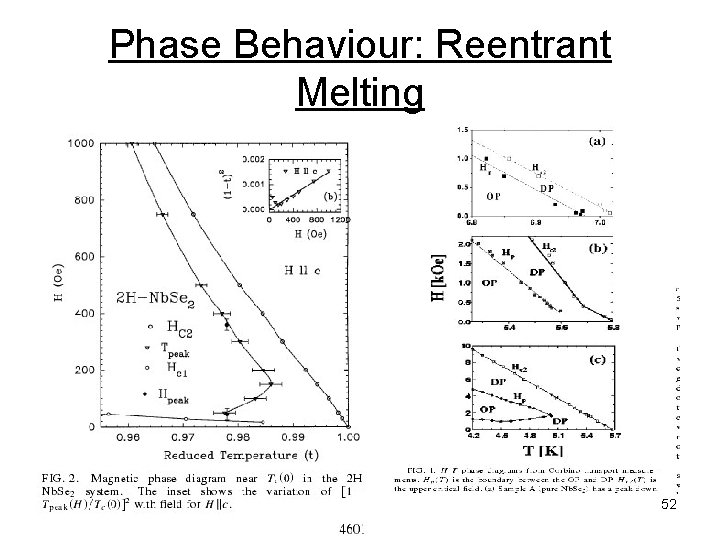
Phase Behaviour: Reentrant Melting 52

The phase diagram angle and a personal angle …. 54

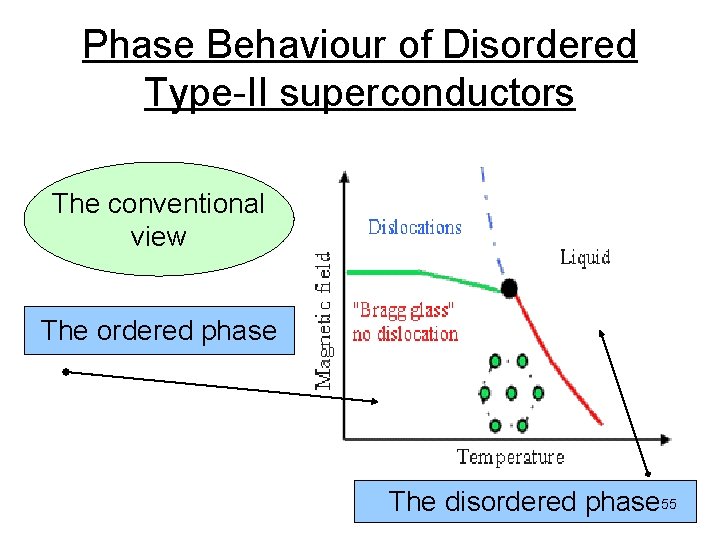
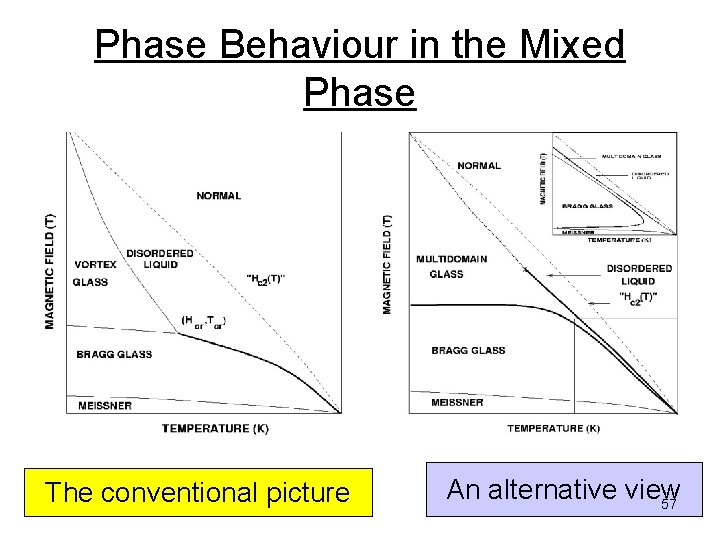
Phase Behaviour of Disordered Type-II superconductors The conventional view The ordered phase The disordered phase 55

Phase Behaviour in the Mixed Phase The conventional picture An alternative view 57

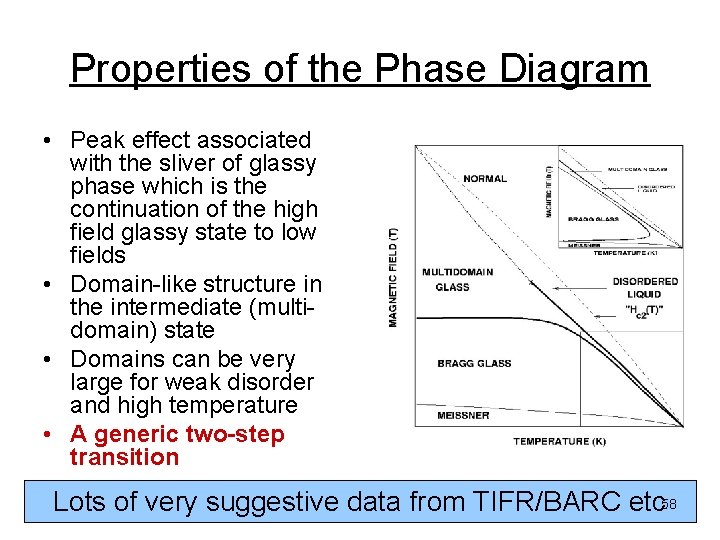
Properties of the Phase Diagram • Peak effect associated with the sliver of glassy phase which is the continuation of the high field glassy state to low fields • Domain-like structure in the intermediate (multidomain) state • Domains can be very large for weak disorder and high temperature • A generic two-step transition Lots of very suggestive data from TIFR/BARC etc 58

The Last Word. . • Alternative approaches: Critical currents may be dominated by surface pinning, effects of surface treatment (Simon/Mathieu). PE seems to survive, though • How to compute the transport properties of the multi-domain glass? • If the Zeldov et al. disordered phase injection at surfaces scenario is correct, what about the simulations? • More theory which is experiment directed • Other peak effects without transitions? 59