The Ferromagnetic Quantum Phase Transition in Metals Dietrich

The Ferromagnetic Quantum Phase Transition in Metals Dietrich Belitz, University of Oregon Ted Kirkpatrick, University of Maryland Acknowledgments: Kwan-yuet Ho Maria -Teresa Mercaldo Rajesh Narayanan Jörg Rollbühler Ronojoy Saha Yan Sang Sharon Sessions Sumanta Tewari Achim Rosch John Toner Thomas Vojta Manuel Brando Malte Grosche Gil Lonzarich Christian Pfleiderer Greg Stewart

Outline Lecture 1: 1. Motivation: Why Quantum Ferromagnets are Interesting 2. Classical Phase Transitions a. Ferromagnets b. Liquid-gas transition c. Superconductors, and liquid crystals Lecture 2: 1. Quantum FM Transitions: General Concepts 2. The Quantum FM Transition, Part I: History 3. The Quantum FM Transition, Part II: General Guidelines Lecture 3: 4. The Fermi Liquid as an Ordered Phase 4 – theory a. A useful example: Classical �� b. Goldstone modes in a Fermi liquid 1. The Quantum FM Transition, Part III a. Generalized Landau theory b. Order-parameter fluctuations c. Effects of quenched disorder

Lecture 4: 8. Exponents and Exponent Relations at Quantum Critical Points 9. “How Close is Close to the Critical Point? ”, or How Hard is it to Measure Quantum Critical Exponents? 10. Phase Separation Away from the Coexistence Curve

Lecture 1 Chennai Lectures 2016

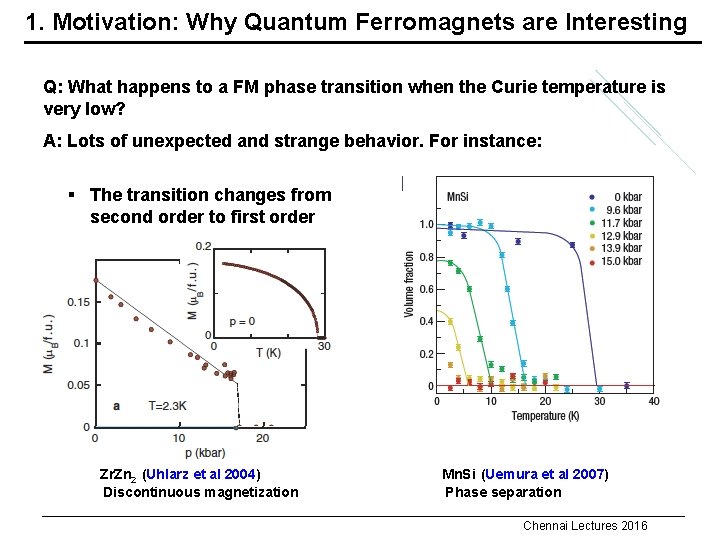
1. Motivation: Why Quantum Ferromagnets are Interesting Q: What happens to a FM phase transition when the Curie temperature is very low? A: Lots of unexpected and strange behavior. For instance: § The transition changes from second order to first order Zr. Zn 2 (Uhlarz et al 2004) Discontinuous magnetization Mn. Si (Uemura et al 2007) Phase separation Chennai Lectures 2016

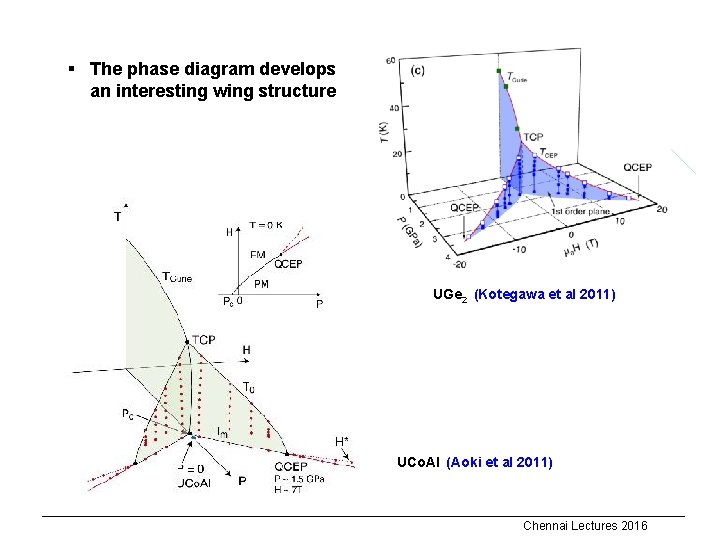
§ The phase diagram develops an interesting wing structure UGe 2 (Kotegawa et al 2011) UCo. Al (Aoki et al 2011) Chennai Lectures 2016

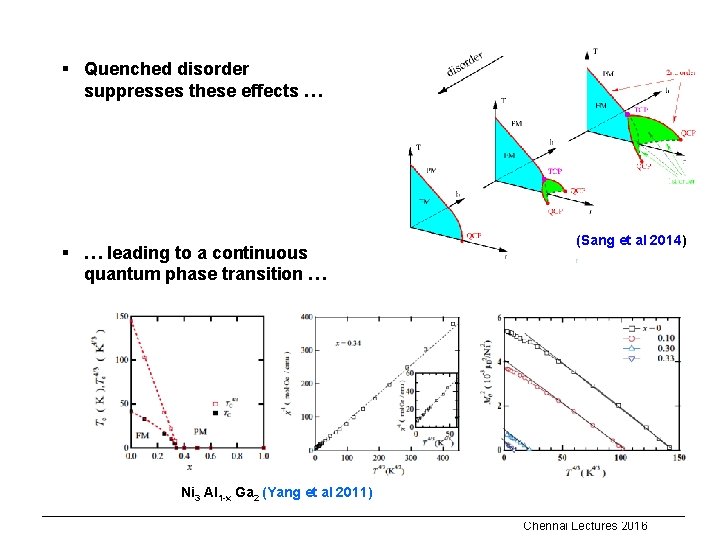
§ Quenched disorder suppresses these effects … § … leading to a continuous quantum phase transition … (Sang et al 2014) Ni 3 Al 1 -x Ga 2 (Yang et al 2011) Chennai Lectures 2016

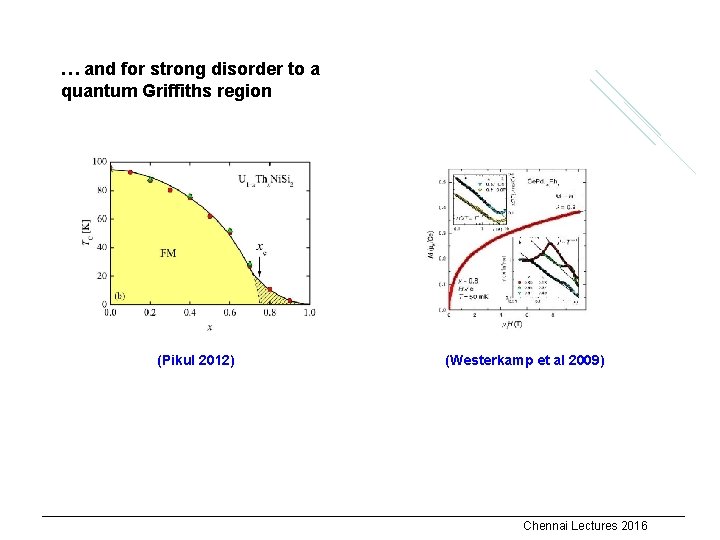
… and for strong disorder to a quantum Griffiths region (Pikul 2012) (Westerkamp et al 2009) Chennai Lectures 2016

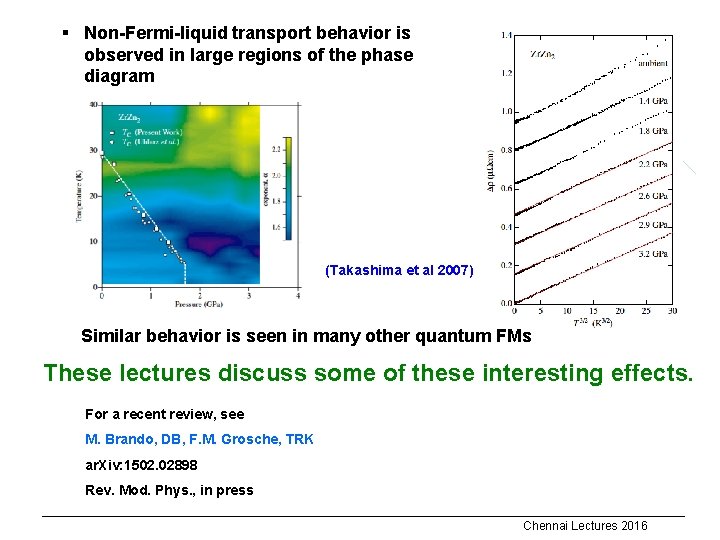
§ Non-Fermi-liquid transport behavior is observed in large regions of the phase diagram (Takashima et al 2007) Similar behavior is seen in many other quantum FMs These lectures discuss some of these interesting effects. For a recent review, see M. Brando, DB, F. M. Grosche, TRK ar. Xiv: 1502. 02898 Rev. Mod. Phys. , in press Chennai Lectures 2016

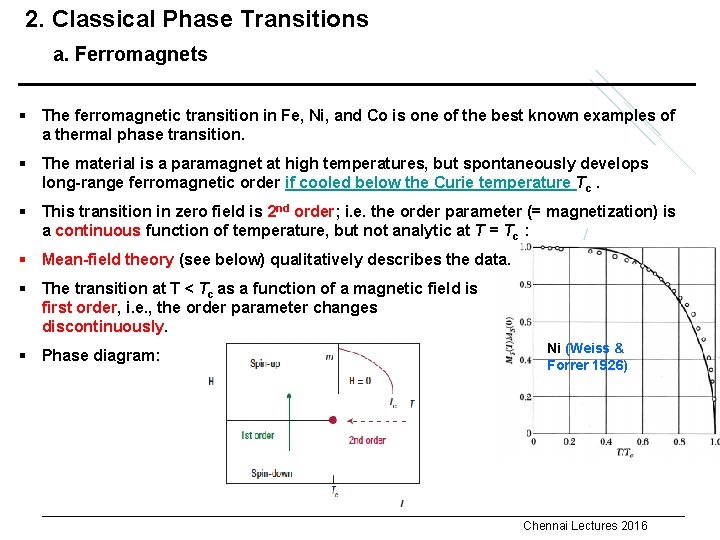
2. Classical Phase Transitions a. Ferromagnets § The ferromagnetic transition in Fe, Ni, and Co is one of the best known examples of a thermal phase transition. § The material is a paramagnet at high temperatures, but spontaneously develops long-range ferromagnetic order if cooled below the Curie temperature Tc. § This transition in zero field is 2 nd order; i. e. the order parameter (= magnetization) is a continuous function of temperature, but not analytic at T = Tc : § Mean-field theory (see below) qualitatively describes the data. § The transition at T < Tc as a function of a magnetic field is first order, i. e. , the order parameter changes discontinuously. § Phase diagram: Ni (Weiss & Forrer 1926) Chennai Lectures 2016

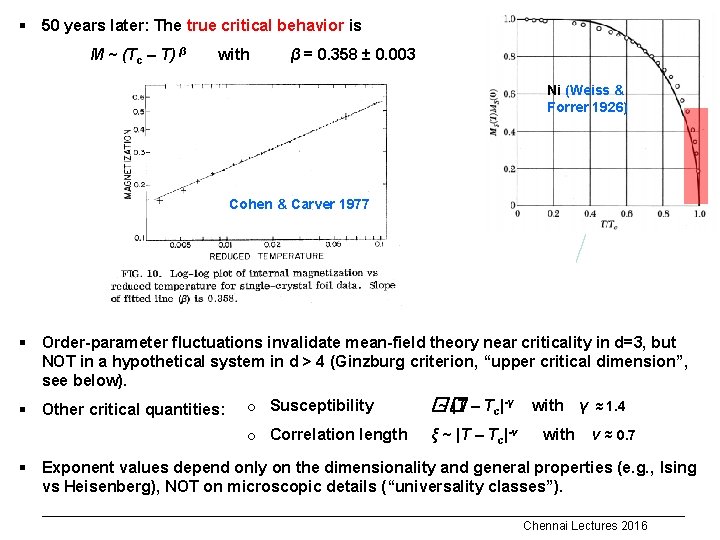
§ 50 years later: The true critical behavior is M ~ (Tc – T) β with β = 0. 358 ± 0. 003 Ni (Weiss & Forrer 1926) Cohen & Carver 1977 § Order-parameter fluctuations invalidate mean-field theory near criticality in d=3, but NOT in a hypothetical system in d > 4 (Ginzburg criterion, “upper critical dimension”, see below). �� ~ |T – Tc|-γ with γ ≈ 1. 4 § Other critical quantities: o Susceptibility o Correlation length ξ ~ |T – Tc|-ν with ν ≈ 0. 7 § Exponent values depend only on the dimensionality and general properties (e. g. , Ising vs Heisenberg), NOT on microscopic details (“universality classes”). Chennai Lectures 2016

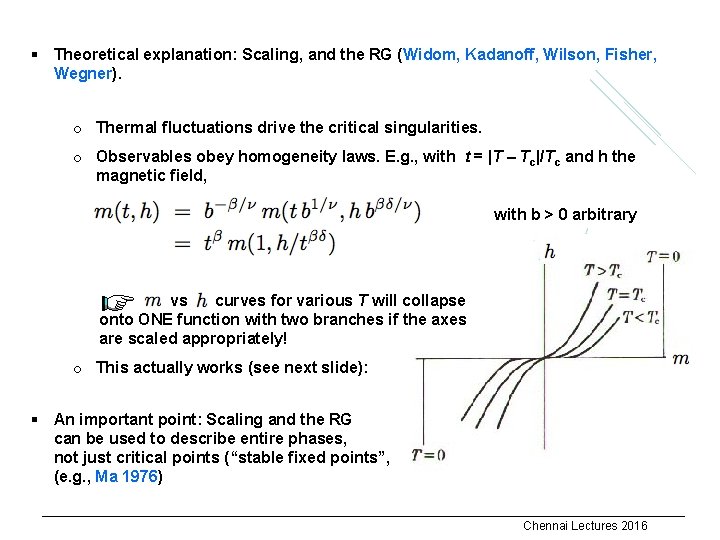
§ Theoretical explanation: Scaling, and the RG (Widom, Kadanoff, Wilson, Fisher, Wegner). o Thermal fluctuations drive the critical singularities. o Observables obey homogeneity laws. E. g. , with t = |T – Tc|/Tc and h the magnetic field, x x with b > 0 arbitrary vs curves for various T will collapse onto ONE function with two branches if the axes are scaled appropriately! o This actually works (see next slide): § An important point: Scaling and the RG can be used to describe entire phases, not just critical points (“stable fixed points”, (e. g. , Ma 1976) Chennai Lectures 2016

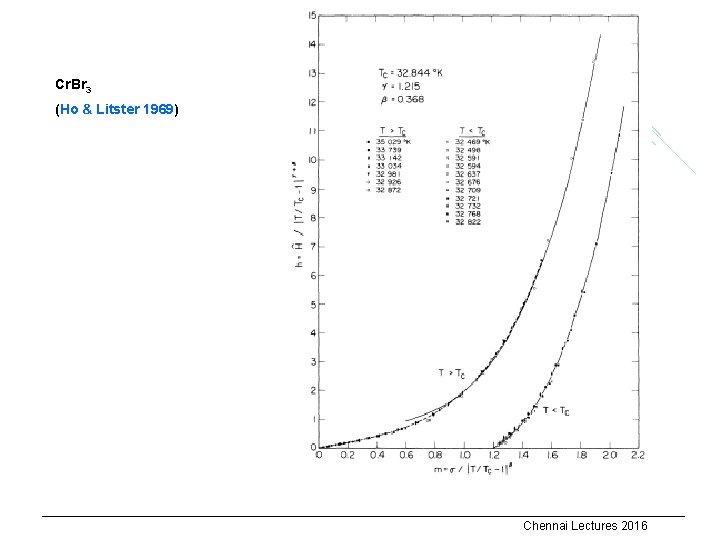
Cr. Br 3 (Ho & Litster 1969) Chennai Lectures 2016

§ “Action” (= Hamiltonian/T), partition function, free energy density for a classical FM: § Mean-field approximation, , Landau free energy 2 nd order transition with mean-field exponents Chennai Lectures 2016

Focus on the susceptibility: § Homogeneous susceptibility: § Generalization to k > 0: x x x § (Ornstein-Zernicke) correlation length diverging length scale, LR correlations § Example of a “soft” or “massless” mode or excitation (here: a critical soft mode) § A time scale also diverges: (“critical slowing down”) § z is called “dynamical critical exponent” § Fluctuations 2 nd order transition with exponents in the appropriate universality class (Ising, XY, or Heisenberg) § Fluctuations are important only below an upper critical dimension (d < 4 in this case); Ginzburg criterion Chennai Lectures 2016

Lecture 2 Chennai Lectures 2016

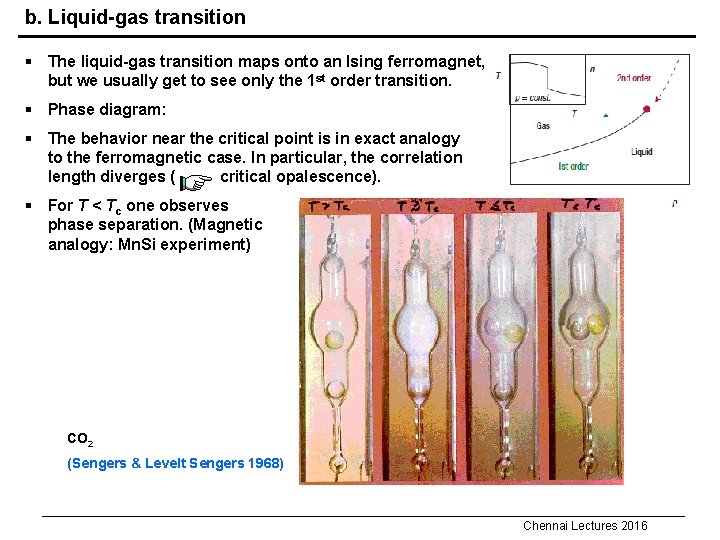
b. Liquid-gas transition § The liquid-gas transition maps onto an Ising ferromagnet, but we usually get to see only the 1 st order transition. § Phase diagram: § The behavior near the critical point is in exact analogy to the ferromagnetic case. In particular, the correlation length diverges ( critical opalescence). § For T < Tc one observes phase separation. (Magnetic analogy: Mn. Si experiment) CO 2 (Sengers & Levelt Sengers 1968) Chennai Lectures 2016

c. Superconductors (and liquid crystals) § Now consider a superconductor with order parameter x x § But, : same as XY ferromagnet couples to the E&M vector potential (photons): § A comes with a gradient A-correlation function diverges as § Photons by themselves are soft (“generic” soft mode), but a nonzero mass! : gives them a § “Integrate out” the photons: x x with an “effective” action x Chennai Lectures 2016

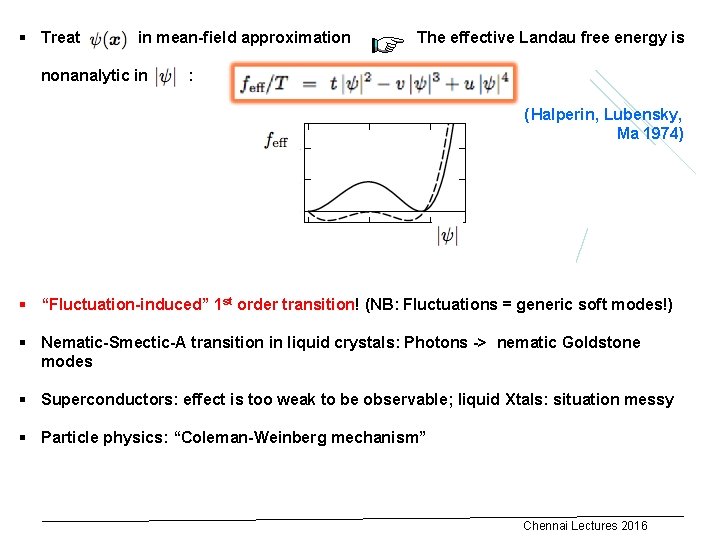
§ Treat in mean-field approximation nonanalytic in The effective Landau free energy is : x x (Halperin, Lubensky, Ma 1974) § “Fluctuation-induced” 1 st order transition! (NB: Fluctuations = generic soft modes!) § Nematic-Smectic-A transition in liquid crystals: Photons -> nematic Goldstone modes § Superconductors: effect is too weak to be observable; liquid Xtals: situation messy § Particle physics: “Coleman-Weinberg mechanism” Chennai Lectures 2016

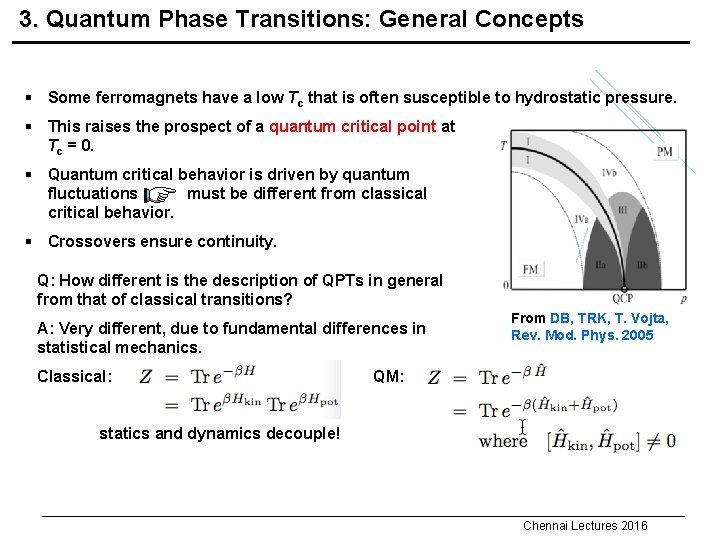
3. Quantum Phase Transitions: General Concepts § Some ferromagnets have a low Tc that is often susceptible to hydrostatic pressure. § This raises the prospect of a quantum critical point at Tc = 0. § Quantum critical behavior is driven by quantum fluctuations must be different from classical critical behavior. § Crossovers ensure continuity. Q: How different is the description of QPTs in general from that of classical transitions? From DB, TRK, T. Vojta, Rev. Mod. Phys. 2005 A: Very different, due to fundamental differences in statistical mechanics. Classical: x x x statics and dynamics decouple! QM: x x Chennai Lectures 2016

§ Solution: Trotter formula (Trotter 1959) § Coherent-state formalism (Casher, Lurie, Revzen 1969) § Divide the interval into infinitesimal slices, and integrate § End result: § is referred to as “imaginary time” (Wick rotation ) § Analytic continuation yields real-time (or frequency) dynamics Statics and dynamics do indeed couple § If , then a quantum system in d spatial dimensions resembles a classical system in d + z dimensions! In general, (Hertz 1976) § Upper critical dimension of classical system implies upper critical dimension of quantum system § Mean-field theory more robust in quantum case! Chennai Lectures 2016

4. The Quantum FM Transition in Metals, Part I: History § Stoner (1937): Mean-field theory for both classical and quantum case Susceptibility: RPA (“spin screening”) with and non-magnetic electrons the relevant interaction constant Transition at (non-thermal control parameter) § Moriya et al (early 1970 s): Self-consistent one-loop theory (aka self-consistent spin fluctuation theory) § Hertz (1976): Developed RG framework for QPTs in general, used metallic FMs as a prime example. § Millis (1993): Used Hertz’s RG framework to determine temperature scaling. Plausibility arguments for Hertz’s action (with a lot of hindsight): • Landau free energy (again): • t is the inverse physical (dressed) susceptibility 1/ x Chennai Lectures 2016

• RPA again: • Generalize everything to nonzero wavevectors and frequencies (Fourier trafo of ) x holds for noninteracting electrons x (Lindhard fct) AND for interacting ones action • § describes the dynamics of clean electrons (“Landau damping”) • Represents coupling of conduction electrons dynamics to the magnetization • At • for classical magnets implies • for quantum magnets Conclusion (as of 1976): Mean-field theory yields exact critical behavior for all d > 1 ( QPTs not very interesting as far as critical behavior goes) Chennai Lectures 2016

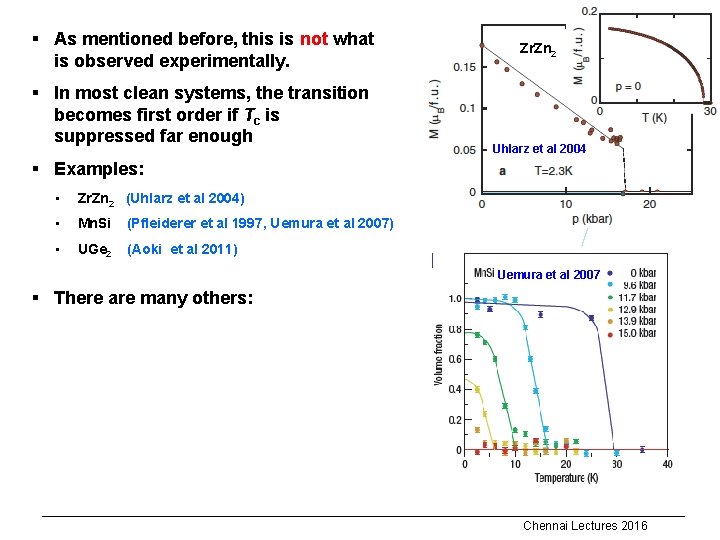
§ As mentioned before, this is not what is observed experimentally. § In most clean systems, the transition becomes first order if Tc is suppressed far enough Zr. Zn 2 Uhlarz et al 2004 § Examples: • Zr. Zn 2 (Uhlarz et al 2004) • Mn. Si (Pfleiderer et al 1997, Uemura et al 2007) • UGe 2 (Aoki et al 2011) Uemura et al 2007 § There are many others: Chennai Lectures 2016

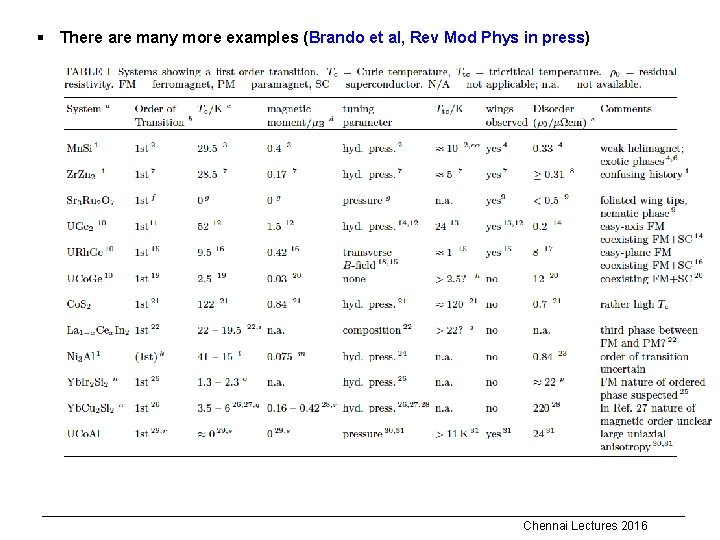
§ There are many more examples (Brando et al, Rev Mod Phys in press) Chennai Lectures 2016

5. The Quantum FM Transition, Part II: General Guidelines Observations: • A tricritical point separates the 2 nd order transitions from the 1 st order ones. • In a magnetic field, tricritical wings appear: • A quantum critical point is eventually realized, but only at a nonzero magnetic field! • This behavior is seen in systems that are very different with respect to electronic structure, type of magnet (Ising, XY, Heisenberg), etc. a The explanation must be universal, i. e. , lie in stat. mech. , not in solid-state effects. x Look for an explanation that involves low-lying excitations (aka soft modes) • These materials are all metals (Kotegawa et al 2011) Conduction electrons likely important Study Fermi liquids first. Q: Don’t we know everything about Fermi liquids, and wasn’t that built into Hertz’s x action? A: NO! Chennai Lectures 2016

Spoiler: The answer in a nutshell: A novel type of fluctuation-induced 1 st x order transition • The leading wavenumber dependence of the inverse susceptibility that enters the action is x for 1 < d < 3 and x for d = 3 • This is a consequence of soft modes in a Fermi liquid, see below • Scaling suggests h ~ k, so this nonanalyticity is also present for function of h. • The magnetization is seen by the conduction electrons as an effective field. In a generalized Landau theory, • • This leads to a generalized Landau free energy x x x which leads to a 1 st-order transition. at k = 0 as a translates into with (DB, TRK, T. Vojta 1999) Conclusion: In clean metals, generic soft modes couple to the ferromagnetic order parameter and make the quantum FM transition generically 1 st order. Chennai Lectures 2016

Lecture 3 Chennai Lectures 2016

6. The Fermi Liquid as an Ordered Phase a. A useful example: Classical ϕ 4 – theory (again) § O(3) ϕ 4 – theory in d spatial dimensions with a field in 1 -direction: § Saddle-point solution for the ordered phase: with x § Fluctuations: Chennai Lectures 2016

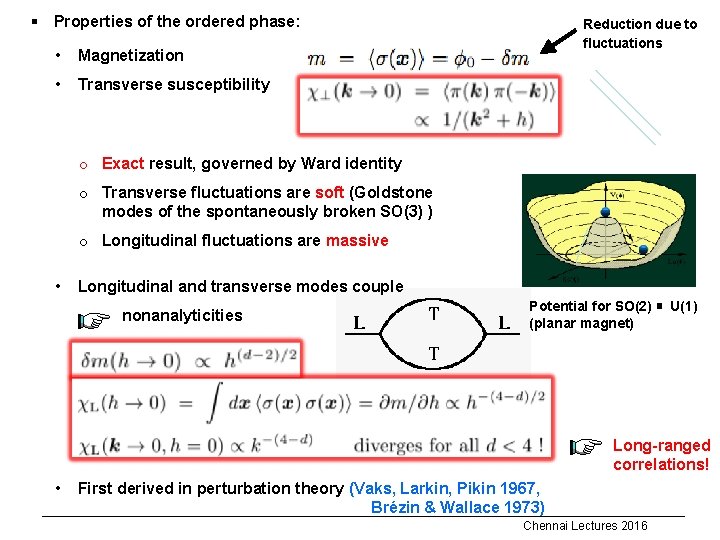
§ Properties of the ordered phase: • Magnetization • Transverse susceptibility Reduction due to fluctuations o Exact result, governed by Ward identity o Transverse fluctuations are soft (Goldstone modes of the spontaneously broken SO(3) ) o Longitudinal fluctuations are massive • Longitudinal and transverse modes couple x nonanalyticities Potential for SO(2) ≅ U(1) (planar magnet) Long-ranged correlations! • First derived in perturbation theory (Vaks, Larkin, Pikin 1967, x Brézin & Wallace 1973) Chennai Lectures 2016

§ Derivation via RG methods: § Expand in powers of fluctuations and gradients, assign scale dimensions, and look for a stable fixed point. The above behavior is exact for all d > 2 and can be described by a § Fixed-point action dimensionless x plus least irrelevant operators, e. g. § This suffices for deriving all scaling behaviors, e. g. § Nonanalyticities are leading corrections to scaling at the stable fixed point § d = 2 is lower critical dimension (Mermin-Wagner ✔ ) Chennai Lectures 2016

§ Note: Similar arguments can be used to exactly characterize nonanalyticities in various other systems, both classical and quantum. For instance, • The shear viscosity in classical fluids has a nonanalytic frequency dependence since it couples to the diffusive transverse-velocity fluctuations. • This is an example of classical long-time tails, i. e. , non-exponential decay of correlation functions. • The conductivity at T = 0 in a disordered metal is a nonanalytic function of the frequency • This is an example of what are called weak-localization and Altshuler-Aronov effects in disordered metals. We will now apply analogous arguments to a clean Fermi liquid. Chennai Lectures 2016

b. Goldstone modes in a Fermi liquid (i) The stable Fermi-liquid fixed point § A long story (Wegner 1970 s, TRK & DB 1997, 2012) made very short: § In a Fermi system at T = 0, there are two-particle excitations that are § The Fermi liquid is an ordered phase characterized by • the soft modes (analogous to π ) that o are controlled by a Ward identity o are Goldstone modes of a spontaneously broken symmetry o have a linear dispersion relation o acquire a mass at T > 0 and h > 0 • These soft modes are the clean analogs of what are called “(spin)-diffusons” in disordered systems, where they lead to weak-localization and Altshuler-Aronov effects. (They are NOT density fluctuations. ) Chennai Lectures 2016

• an order parameter given by the DOS at the Fermi surface (more precisely: By the spectrum of the Green’s function): • an order-parameter susceptibility (analogous to • a stable RG fixed point with fixed-point action ) all other terms are RG irrelevant! x a • Scale dimensions • Least irrelevant operators with scale dimension § This allows for the derivation of homogeneity laws that yield the exact leading nonanalyticities in a Fermi liquid! Chennai Lectures 2016

(ii) Universal properties of the Fermi liquid § DOS: Jiang et al 2006 • analogous to • agrees with perturbative results (Khveshchenko & Reizer 1998) § Spin susceptibility: § first derived in perturbation theory (DB, TRK, T Vojta 1997; Betouras et al 2005) § NB the sign of the effect! § Soft modes long-ranged correlations nonanalytic behavior Chennai Lectures 2016

7. The Quantum Ferromagnetic Transition, Part III a. Generalized Landau theory § Ordinary Landau theory: with t = 1/ the inverse susceptibility § Now recall the argument given earlier: • • acts as an effective field in a metal, the FL Goldstone modes couple to via a Zeeman term via the nonanalytic h – dependence of ! x § The FL Goldstone modes lead to a generalized Landau theory: The quantum ferromagnetic transition in clean metals in zero field is generically 1 st order ! Chennai Lectures 2016

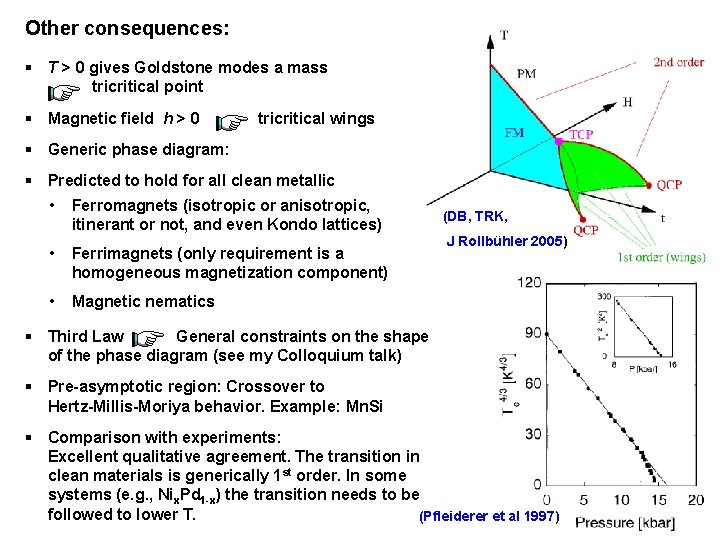
Other consequences: § T > 0 gives Goldstone modes a mass x tricritical point § Magnetic field h > 0 tricritical wings § Generic phase diagram: § Predicted to hold for all clean metallic • Ferromagnets (isotropic or anisotropic, itinerant or not, and even Kondo lattices) • Ferrimagnets (only requirement is a homogeneous magnetization component) • Magnetic nematics (DB, TRK, J Rollbühler 2005) § Third Law General constraints on the shape of the phase diagram (see my Colloquium talk) § Pre-asymptotic region: Crossover to Hertz-Millis-Moriya behavior. Example: Mn. Si § Comparison with experiments: Excellent qualitative agreement. The transition in clean materials is generically 1 st order. In some systems (e. g. , Nix. Pd 1 -x) the transition needs to be followed to lower T. (Pfleiderer et al 1997) Chennai Lectures 2016

b. Order-parameter fluctuations § Technical derivation: Coupled field theory for fermions and OP fluctuations. • Treat conduction electrons in a tree approximation • 1 -loop order • Higher order: Only prefactors change Hertz’s action nonanalyticities appear Q: How good or bad is the mean-field approximation? A: Nobody really knows, but: • OP fluctuations are above their upper critical dimension • In liquid crystals, they are below the upper critical dimension • This makes it plausible that the 1 st order transition in quantum ferromagnets is much more robust than in liquid crystals. Other suggestions for avoiding a quantum critical point : • Textured phases (spiral, etc), with the length scale set by the maximum in (Chubukov et al, Green et al) Chennai Lectures 2016

c. Effects of quenched disorder Quenched disorder changes things drastically: § The generic soft modes are now diffusive § The susceptibility now is x x (Altshuler et al early 1980 s) x and by the same arguments as before we have, in d = 3, NB the sign! (TRK & DB 1996) § This predicts a 2 nd order transition with non-mean-field exponents. § For instance, , and , consistent with many observed phase diagrams (see below for other interpretations) § Order-parameter fluctuations lead to log-normal modifications of the power laws (DB et al 2001) § Increasing the disorder from the clean limit decreases the tricritical temperature continuously (Pikul et al 2012) Chennai Lectures 2016

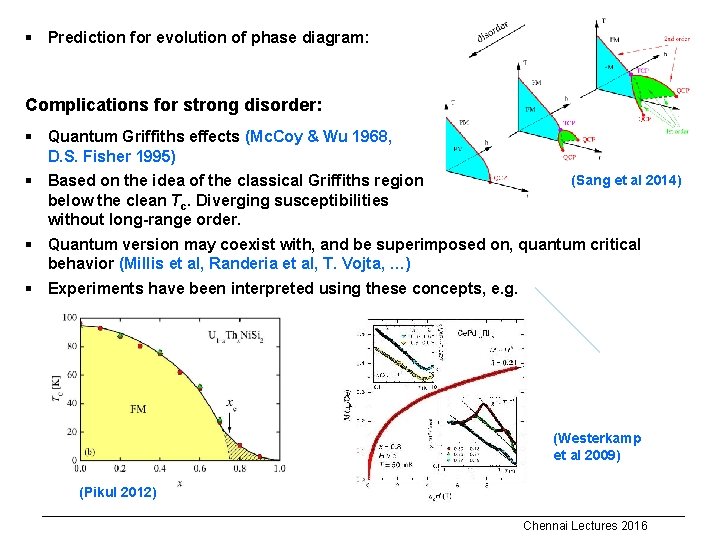
§ Prediction for evolution of phase diagram: Complications for strong disorder: § Quantum Griffiths effects (Mc. Coy & Wu 1968, D. S. Fisher 1995) § Based on the idea of the classical Griffiths region below the clean Tc. Diverging susceptibilities without long-range order. (Sang et al 2014) § Quantum version may coexist with, and be superimposed on, quantum critical behavior (Millis et al, Randeria et al, T. Vojta, …) § Experiments have been interpreted using these concepts, e. g. (Westerkamp et al 2009) (Pikul 2012) Chennai Lectures 2016

Lecture 4 Chennai Lectures 2016

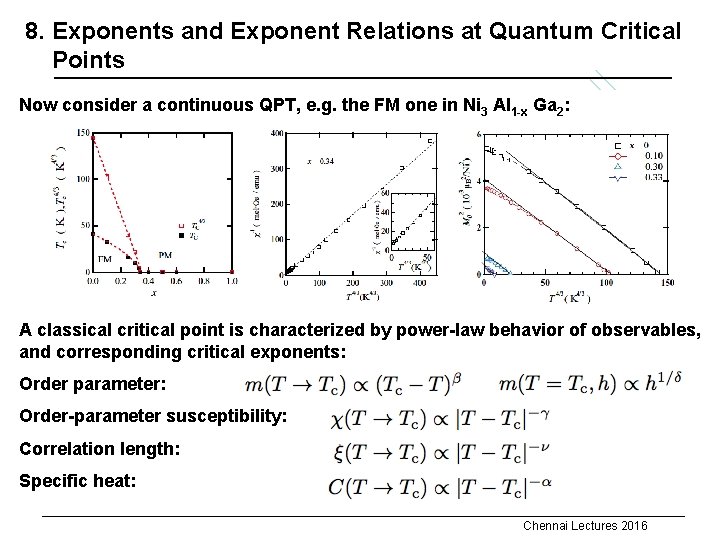
8. Exponents and Exponent Relations at Quantum Critical x Points Now consider a continuous QPT, e. g. the FM one in Ni 3 Al 1 -x Ga 2: A classical critical point is characterized by power-law behavior of observables, and corresponding critical exponents: Order parameter: Order-parameter susceptibility: Correlation length: Specific heat: Chennai Lectures 2016

A quantum critical point we can approach at T = 0 by varying the non-thermal control parameter t, or at t = 0 by letting T -> 0. We need more critical exponents! Order parameter: Order-parameter susceptibility: Correlation length: The specific heat vanishes at T = 0 => Consider the Specific-heat coefficient: Chennai Lectures 2016

The T- exponents will in general be different from the t- exponents! What is the relation? Various points towards an answer: § In quantum statistical mechanics, inverse temperature is related to (imaginary) time. => T- scaling is governed by a dynamical exponent z that describes how the relaxation time diverges as a function of the relaxation length: § Power laws result from generalized homogeneity laws for observables with b an arbitrary length rescaling factor and x (and r = t, sorry!). : a scaling function Put b = r-ν => At r = 0 we have with § Conclusion: If describes the static scaling behavior, then describes the temperature scaling behavior § Caveat: This is true only under special circumstances. More generally, the Tscaling of may be described by A z, rather than by THE z, due to multiple time scales and/or dangerous irrelevant variables. Chennai Lectures 2016

That’s a lot of exponents. How many are independent? First consider a classical transition. Look at the homogeneity law for the order parameter: => ✓ ✓ Now, the susceptibility is a thermodynamic derivative of : This yields => => “Widom’s equality” Similar arguments lead to, e. g. , “Essam-Fisher equality” “Fisher equality” Chennai Lectures 2016

Some exponent relations depend explicitly on the dimensionality, e. g. “hyperscaling” They are not valid if the dimensionality is larger than the “upper critical dimension”. For many classical transitions, that’s d = 4. Classically, only two exponents are independent. These exponent relations all depend on various forms of scaling being valid. While that’s usually the case at critical points, there is no guarantee. Weaker statements that depend only on thermodynamic stability take the form of rigorous inequalities. For instance, “Rushbrooke inequality” In disordered systems, a rigorous lower bound on the correlation length exponent is known: Chayes, Spencer, Fisher (1986) (See also the “Harris criterion”). Chennai Lectures 2016

At quantum critical points, some of the classical relations still hold, e. g. , Widom Fisher Analogous relations hold for the T- exponents: Others change. For instance, a generalization of Essam-Fisher becomes where and are the dynamical exponents that govern the T – dependence of the order parameter and the specific heat, respectively. These two are in general NOT the same! The rigorous Rushbrooke inequality holds for the T – exponents: but gets modified for the t – exponents: Chennai Lectures 2016

Hyperscaling relations, e. g. , again hold only below some upper critical dimensionality, which tends to be lower for quantum phase transitions than for classical ones. Overall, at a quantum critical point there at least two independent static critical exponents, plus the dynamical ones. Depending on what form of scaling holds (which depends on the critical point and the dimensionality) there may be as many as five independent static exponents. For details, see Chennai Lectures 2016

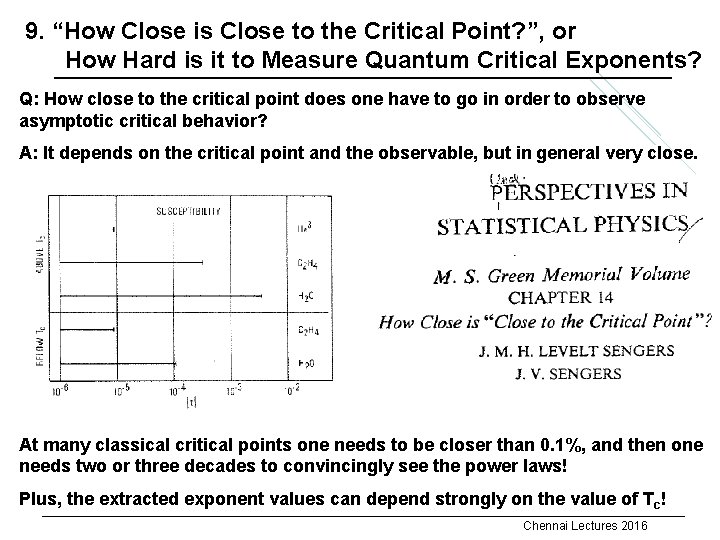
9. “How Close is Close to the Critical Point? ”, or x How Hard is it to Measure Quantum Critical Exponents? Q: How close to the critical point does one have to go in order to observe asymptotic critical behavior? A: It depends on the critical point and the observable, but in general very close. At many classical critical points one needs to be closer than 0. 1%, and then one needs two or three decades to convincingly see the power laws! Plus, the extracted exponent values can depend strongly on the value of T c! Chennai Lectures 2016

Farther away from criticality one often observes effective power laws with exponents that are controlled by unstable RG fixed points. There is no reason to believe that requirements at quantum critical points are less stringent. Various issues: § Many quantum critical points are controlled by chemical composition. This is hard to control, and the critical concentration is typically not known very precisely. § Additional physics can mask quantum criticality, e. g. , quantum Griffiths effects in many disordered quantum ferromagnets. Chennai Lectures 2016

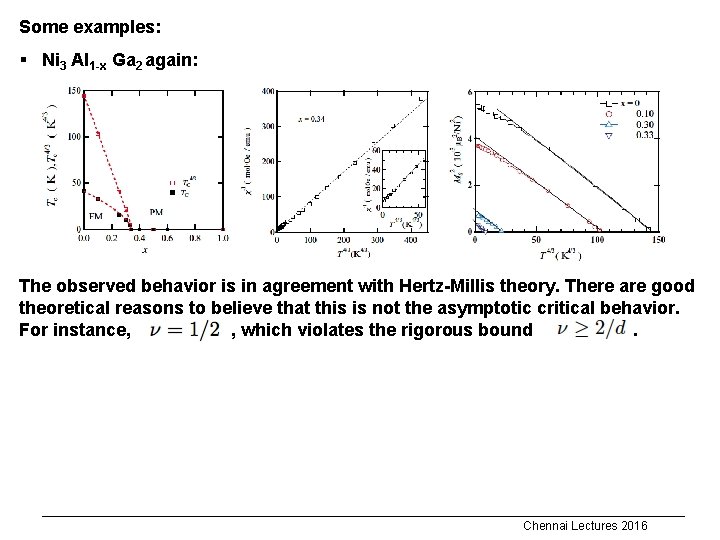
Some examples: § Ni 3 Al 1 -x Ga 2 again: The observed behavior is in agreement with Hertz-Millis theory. There are good theoretical reasons to believe that this is not the asymptotic critical behavior. For instance, , which violates the rigorous bound. Chennai Lectures 2016

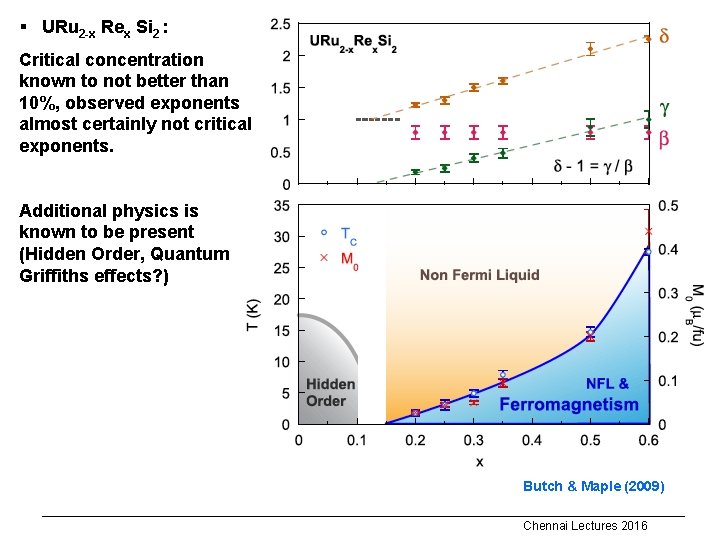
§ URu 2 -x Rex Si 2 : Critical concentration known to not better than 10%, observed exponents almost certainly not critical exponents. Additional physics is known to be present (Hidden Order, Quantum Griffiths effects? ) Butch & Maple (2009) Chennai Lectures 2016

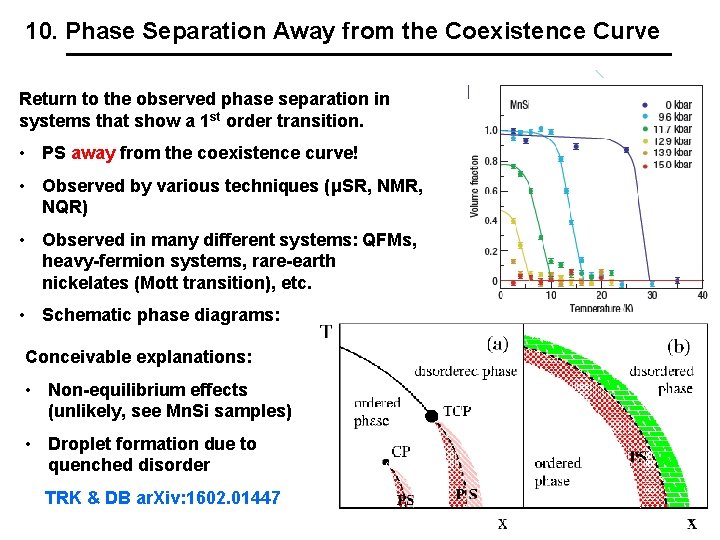
10. Phase Separation Away from the Coexistence Curve Return to the observed phase separation in systems that show a 1 st order transition. • PS away from the coexistence curve! • Observed by various techniques (μSR, NMR, NQR) • Observed in many different systems: QFMs, heavy-fermion systems, rare-earth nickelates (Mott transition), etc. • Schematic phase diagrams: Conceivable explanations: • Non-equilibrium effects (unlikely, see Mn. Si samples) • Droplet formation due to quenched disorder TRK & DB ar. Xiv: 1602. 01447 Chennai Lectures 2016

Summary § The quantum ferromagnetic transition in clean metals is generically 1 st order. § This can be understood as a fluctuation-induced 1 st order transition due to the coupling of the magnetization to generic soft modes in metals (clean versions of diffusons). § The Fermi liquid can be understood as an ordered phase with a broken symmetry, with the generic soft modes as Goldstone modes. § At nonzero temperature there is a tricritical point, and tricritical wings. § Good agreement between theory and experiments. § Quenched disorder changes a crucial sign, leading to a 2 nd order transition. Strong disorder leads to additional complications. § Additional critical exponents are needed for QCPs. § True critical behavior is hard to observe. In classical systems it took decades to obtain reliable exponents. For QCPs, experiments are probably still far from the necessary level of precision. § Phase separation away from a coexistence curve requires an explanation. Suggestion: Droplet formation due to quenched disorder. Chennai Lectures 2016

Recommended Reading Quantum Ferromagnets: • M. Brando et al, ar. Xiv: 1502. 02898, Rev. Mod. Phys. , in press Generic Scale Invariance: • DB, TRK, Thomas Vojta, Rev. Mod. Phys. 77, 579 (2005) Quantum Phase Transitions: • J. Hertz, Phys. Rev. B 14, 1165 (1976) • S. Sachdev, Quantum Phase Transitions (Cambridge Univ. Press 1999) Scaling, and Renormalization Group: • H. E. Stanley, Introduction to Phase Transitions and Critical Phenomena (Oxford Univ. Press 1971) • S. -K. Ma, Modern Theory of Critical Phenomena (Perseus 1976) • M. E. Fisher, in Advanced Course on Critical Phenomena, F. W. Hahne (ed. ) (Springer 1983) • J. Cardy, Scaling and Renormalization in Statistical Physics (Cambridge Univ. Press 1996) Chennai Lectures 2016