Teorija igara Uvod U svakodnevnom ivotu podjednako poslovnom

Teorija igara

Uvod U svakodnevnom životu, podjednako poslovnom i privatnom, okolina u kojoj djelujemo promjenjiva je i dinamična i u njoj susrećemo pojedince ili (interesne) grupe čije su aktivnosti i djelovanja u odlučivanju relevantna, a ponekad i presudna za naše odluke.

Uvod u teoriju igara o Malo je vjerojatno da postoji netko nikada nije ušao u sportsku kladionicu da odigra „keca“ ili „dvojku“ ili igrao igre na sreću gdje „svaka dobiva“. o “siguran par, dobitak garantiran“ – što se ustvari krije iza tih parova, tombole, lutrije i kladionice? o Krije se nešto je puno širi pojam od kladionice ili pobjede i poraza. o Krije se znanost koja je utkana u sve sfere života. Krije se, običnim ljudima nepoznata, teorija igara.

Uvod u teoriju igara o Teorija igara sadrži strategiju kao najsavršeniji pojam u igri. o Što je to strategija koju primjenjuju igrači u igri? Tko su igrači? Što je igra? o Igra je lijepa stvar, lijepo je biti igrač. Sjajno je biti strateg. Ali samo kad se radi o zabavi. o Teorija igara je svuda oko nas. U svim područjima života služimo se različitim strategijama u interakciji s drugim ljudima, a teorija igara pomaže nam u analizama strateških problema u različitim okruženjima kao što su, primjerice, obiteljske svađe, međususjedski odnosi ili sporovi…

- Razvoj teorije igara o Matematička disciplina koja se razvila sredinom 20. st. o Davno prije formiranja teorije igara njezina ideja utjecala je na razne vojskovođe i njihove ratne strategije. o Formalni začeci teorije igara pripisuju se Jamesu Waldegraveu, izumitelju kartaške igre Le Her koji je prvi puta predložio formu minmax – rješenja mješovite strategije igre za dvije osobe.

o Doprinos teoriji igara dali su matematičar John von Neumann i ekonomist Oskar Morgenstern kroz knjigu “Teorija igara i ekonomsko ponašanje” (Theory of Games and Economic Behavior) o Prvi put se eksplicitno povezuje teorija igara s ekonomijom

o 1950. godine prvi put predstavljena igra poznata pod nazivom zatvorenikova dilema (Prisioner's Dillema) o 1974. objavljena knjiga „Values of Non – Atomic Games“ koja se bavi vrijednostima u velikim igrama u kojima su pojedinačno svi igrači beznačajni

o Doprinos teoriji igara dao je i John Nash u svom radu: Non-cooperative games, Annals of Mathematics o O Johnu Nashu je i snimljen biografski film: Genijalni um

Teorija igara Analizira donošenje odluka u konfliktnim situacijama pri čemu svaki od sudionika u igri nastoji promovirati vlastiti interes, poštujući pravila igre i koristeći različite strategije kako bi sebi osigurao povoljan ishod igre. o Cilj odrediti ponašanje sudionika koje je za njih najpovoljnije – optimalna strategija o Zadatak pronalaženje rješenja u situacijama konkurencije u kojima se djelomično ili potpuno sukobljavaju interesi najmanje dva protivnika

- Teorija igara bavi se proučavanjem: o o Grupa Interakcija Strategija Razum Primjer 1: Zajednička izrada seminarskog rada iz kolegija Menadžersko odlučivanje - U terminologiji teorije igara sljedeće situacije nisu igre: o o Jednostrana odluka Preveliki utjecaj

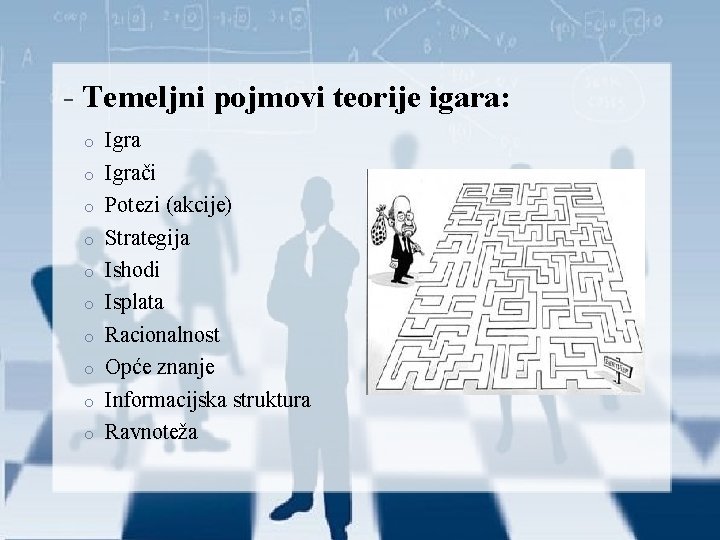
- Temeljni pojmovi teorije igara: o o o o o Igrači Potezi (akcije) Strategija Ishodi Isplata Racionalnost Opće znanje Informacijska struktura Ravnoteža

o Igra – sukob interesa između pojedinaca odnosno igrača. o Opis strateških interakcija te uključuje ograničenja za akcije i interese igrača. o Skup pravila i dogovora po kojima se igrači ravnaju o Grupa – u svakoj igri postoji nekoliko donositelja odluke koje se nazivaju igrači (najmanje dva) o Strategija – izbori igrača koje oni imaju na raspolaganju u igri. Postoje dvije osnovne vrste, a to su čista i mješovita. o Razum – svaki igrač bira za sebe najbolju moguću akciju o Konačno stanje / rezultat – svaka pojedina realizacija igre

- Pitanja koja igrači imaju dok igraju igru su: o Koje će poteze protivnički igrači odigrati? o Kako će koji protivnik igrati? o Koje će biti posljedice tog poteza te kako će one utjecati na cijelu grupu?

Teorija igara u širem smislu Igre vještine Igre na sreću Strateške igre (Teorija igara u užem smislu) Izvor: Kopal, R. , Korkut, D. : Teorija igara, Comminus i Visoka poslovna škola Libertas, Zagreb, 2011.

Igre vještine o o igrač ima potpunu kontrolu nad ishodima o rješavanje križaljke, o polaganje ispita, o utrka na 100 metara i sl. Međutim, ove igre ne bi trebale biti klasificirane kao igre jer im nedostaje osnovni sastojak svih igara, a to je međuovisnost.

Igre na sreću o Igre protiv prirode s jednim igračem o Igrač nema potpunu kontrolu nad ishodima o Njihove strateške odluke ne vode nužno unaprijed određenim ishodima o Ishodi u ovim igrama ovise dijelom o igračevu izboru, a dijelom o sreći, slučaju, „sudbini“

Igre na sreću Razlikuju se: o igre s rizikom i o igre s nesigurnošću.

Igre s rizikom Igrač može dodijeliti vjerojatnost svakom potezu prirode Zna vjerojatnost mogućeg uspjeha svake od svojih strategija Mogu se, na primjer, riješiti na temelju koncepta očekivane vrijednosti.

Igre s nesigurnošću o Također, jedan igrač igra protiv prirode o Potezima prirode igrač ne može dodijeliti vjerojatnosti o Nesigurnost znači da nisu poznati ishodi ni vjerojatnosti pojedinih ishoda o U takvim se okolnostima za rješavanje ovih igara predlažu tri principa : o o o maxmax, maxmin i minmax.

Strateške igre o Igre s dva ili više igrača o Svaki ima djelomičnu kontrolu nad ishodima o Isključujući pri tome prirodu o Ogleda se u postojanju značajnih interakcija među igračima.

Teorija igara u užem smislu Bavi se situacijama koje imaju sljedeća svojstva: o postoje minimalno dva igrača, o igra počinje tako da jedan ili više igrača izaberu između određenih alternativa, o nakon što je izbor pridružen prvom potezu, rezultat je određena situacija koja određuje tko vrši sljedeći izbor i koje su mu alternative „otvorene“, o pravila igre određuju način ponašanja igrača, o svaki potez u igri završava situacijom koja određuje isplatu svakog igrača.

Segmenti teorije igara Tri su osnovna segmenta raščlambe strateških igara: 1. Strateško okruženje : – Tko su igrači? (donositelji odluka) – Koje su raspoložive strategije? (moguće ili izvedive akcije) – Koje su isplate? (ishodi ili ciljevi) Igrači mogu biti pojedinci, skupine, organizacije ili u nekim slučajevima sama priroda. Strateško okruženje odnosi se na interakcije među igračima Različiti igrači razmišljaju na sličan način o istim stvarima i u isto vrijeme Igrači osmišljavaju strategije koje vode različitim ishodima s različitim pripadajućim isplatama. o o

Segmenti teorije igara 2. Pravila igre : – – Koji je vremenski okvir za donošenje odluka? Kakva je priroda sukoba? Kakva je priroda interakcije? Koje su dostupne informacije? o Pravila igre sadrže informacije o identitetu igrača, njihovu znanju o igri, mogućim potezima ili akcijama i njihovim isplatama. o Pravila igre detaljno opisuju način na koji ponašanje jednog igrača utječe na isplate drugoga, ona predstavljaju opće znanje.

Segmenti teorije igara 3. Pretpostavke: – – Racionalnost Opće znanje o Racionalnost podrazumijeva da je svaki igrač motiviran maksimalizacijom vlastitih isplata o Igrač je racionalan ako ima ispravno definirane ciljeve iz skupa mogućih ishoda i u postizanju tih ciljeva primjenjuje najbolju moguću strategiju o Pravila igre detaljno opisuju način na koji ponašanje jednog igrača utječe na isplate drugoga, ona predstavljaju opće znanje.

Igre sa sumom nula o Imamo samo 2 igrača o Jednopotezna igra o Dobitak prvog igrača jednak je gubitku drugog igrača, i obrnuto → zbroj isplata je uvijek 0 o Igrači imaju konačan broj strategija (mogućnosti) za ponašanje u sukobu o “par – nepar’’ o Pretpostavka je da se igra ponavlja

Igre sa sumom nula o Imamo samo 2 igrača o Jednopotezna igra o Dobitak prvog igrača jednak je gubitku drugog igrača, i obrnuto → zbroj isplata je uvijek 0 o Igrači imaju konačan broj strategija (mogućnosti) za ponašanje u sukobu o “par – nepar’’ o Pretpostavka je da se igra ponavlja

Igra “pismo – glava” Sudionici: igrač X i igrač Y Jednopotezna igra (svaki igrač može povući samo jedan potez) Mogućnosti: okrenuti novčanicu na stranu “glave” – strategija I ili “pisma” – strategija II Ukoliko su oba igrača okrenuli “glavu” ili “pismo” pobjedinik je igrač X, a ukoliko je jedan igrač izabrao “glavu” a drugi “pismo” pobjednik je igrač Y

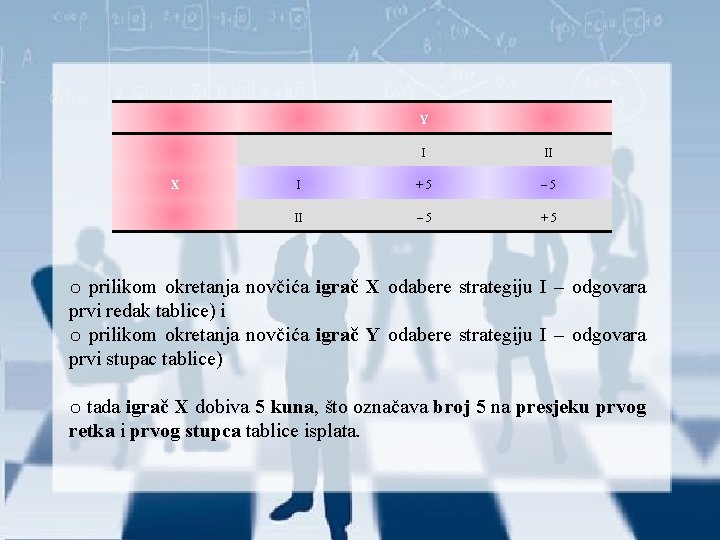
Y X I II I + 5 – 5 II – 5 + 5 o prilikom okretanja novčića igrač X odabere strategiju I – odgovara prvi redak tablice) i o prilikom okretanja novčića igrač Y odabere strategiju I – odgovara prvi stupac tablice) o tada igrač X dobiva 5 kuna, što označava broj 5 na presjeku prvog retka i prvog stupca tablice isplata.

Y X I II I + 5 – 5 II – 5 + 5 o prilikom okretanja novčića igrač X odabere strategiju I – odgovara prvi redak tablice) i o prilikom okretanja novčića igrač Y odabere strategiju II – odgovara drugi stupac tablice) o tada igrač X gubi 5 kuna, a igrač Y dobiva 5 kuna što označava broj – 5 na presjeku prvog retka i drugog stupca tablice isplata. o U oba slučaja dobitak jednoga igrača jednak je gubitku drugoga igrača, pa je zbroj dobitaka oba igrača jednak nuli.

Igra “par – nepar”

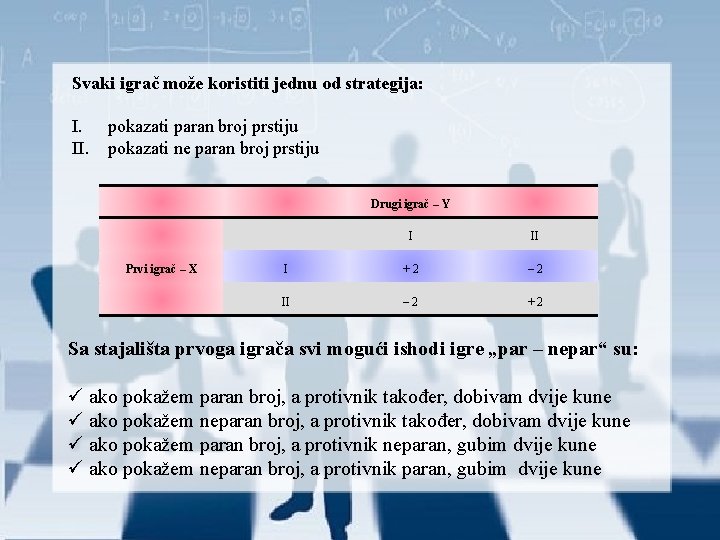
Svaki igrač može koristiti jednu od strategija: I. pokazati paran broj prstiju II. pokazati ne paran broj prstiju Drugi igrač – Y Prvi igrač – X I II I + 2 – 2 II – 2 + 2 Sa stajališta prvoga igrača svi mogući ishodi igre „par – nepar“ su: ü ako pokažem paran broj, a protivnik također, dobivam dvije kune ü ako pokažem neparan broj, a protivnik također, dobivam dvije kune ü ako pokažem paran broj, a protivnik neparan, gubim dvije kune ü ako pokažem neparan broj, a protivnik paran, gubim dvije kune

- Igra sa sedlom o Igrači izabiru različite strategije, te nastoje izabrati najbolje strategije kako bi maksimizirali svoj minimalni dobitak odnosno minimizirali svoj maksimalni gubitak. o Striktno determinirane igre koje primjenjuju čistu strategiju. o Koriste dva kriterija, a to su von Neumann-ov kriterij (minimax) i dominacija.

o o o U igri sudjeluju 2 igrača Igrači su suparnici Pretpostavka je da su oba inteligentna Igrač poštuje strategiju od protivnika Igra se putem matrice plaćanja Cilj je pronaći sedlastu točku

- Pravila igre sa sedlom o zapisivanje u obliku tablice ili u obliku matrice o redovi predstavljaju strategije igrača A, a stupci su strategije igrača B o rezultat igre je srednji rezultat kojeg čine elementi matrice igrača A pri odgovarajućem paru strategija

o Matrica igre = matrica cijene = platežna matrica o RJEŠENJE IGRE ≠ VRIJEDNOST IGRE o Rješenje igre: potez prvog i potez drugog igrača o Vrijednost igre: dobitak prvog igrača i gubitak drugog igrača • Pozitivan predznak – dobitak prvog igrača, a gubitak drugog igrača • Negativan predznak – prvi igrač je ostvario gubitak, a drugi dobitak

- Svrha igre o da igrač A izabere strategiju koja će maksimizirati njegov minimalni dobitak (maxmin), a da igrač B bira onu strategiju koja predstavlja minimum njegovog maksimalnog gubitka (minmax)

o maxmin ≤ minmax • maxmin = donja vrijednost igre • minmax = gornja vrijednost igre o maxmin = minmax = vrijednost igre sedlastu točku igra ima o igra može imati i više sedlastih točaka o sedlasta točka ne mora biti optimalna strategija.

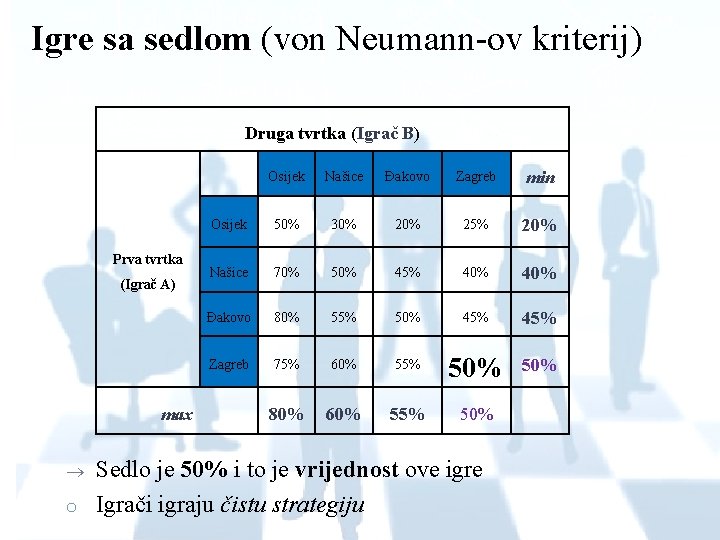
Igre sa sedlom (von Neumann-ov kriterij) Druga tvrtka (Igrač B) Prva tvrtka (Igrač A) max o Osijek Našice Đakovo Zagreb min Osijek 50% 30% 25% 20% Našice 70% 50% 45% 40% Đakovo 80% 55% 50% 45% Zagreb 75% 60% 55% 50% 80% 60% 55% 50% Sedlo je 50% i to je vrijednost ove igre Igrači igraju čistu strategiju

o Rješenje: o Pronalaženje minimalnog elementa svakog reda koji su u ovom slučaju bili 20%, 45%, 50%, te utvrđivanje maksimalnog elementa svakog stupca, koji su u ovom primjeru iznosili 80%, 60%, 55%, 50% o Pronalaženje najvećeg minimalnog elementa koji je u navedenom primjeru 50% , te najmanjeg maksimalnog elementa, koji iznosi također 50%. o Zaključak: maksimum minimuma redova 50% je identičan minimumu maksimuma stupaca koji također iznosi 50% Vrijednost igre je 50%

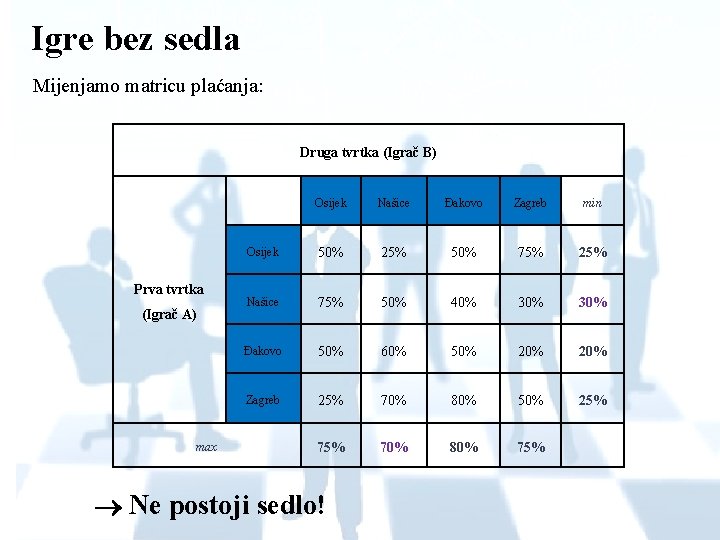
Igre bez sedla Mijenjamo matricu plaćanja: Druga tvrtka (Igrač B) Prva tvrtka (Igrač A) max Osijek Našice Đakovo Zagreb min Osijek 50% 25% 50% 75% 25% Našice 75% 50% 40% 30% Đakovo 50% 60% 50% 20% Zagreb 25% 70% 80% 50% 25% 70% 80% 75% Ne postoji sedlo!

o Igrači igraju mješovitu strategiju koristimo Müller-Merbach-ovu metodu 1. Postavljamo funkciju cilja i restrikcije – primjer za igrača A Simpleks metoda on želi maksimizirati svoj minimalni dobitak – V S varijablama x 1, x 2, x 3 i x 4 označavamo relativnu učestalost izbora Osijeka, Našica, Đakova ili Zagreba kao potencijalne podružnice međunarodne tvrtke 2.

Igrač A Druga tvrtka (Igrač B) Prva tvrtka (Igrač A) max Osijek Našice Đakovo Zagreb min Osijek 50% 25% 50% 75% 25% Našice 75% 50% 40% 30% Đakovo 50% 60% 50% 20% Zagreb 25% 70% 80% 50% 25% 70% 80% 75% D = V max – funkcija cilja (V je dobitak jednog, tj. gubitak drugog igrača, u ovom slučaju je V minimalni dobitak koji se želi maksimizirati) ax 1 + cx 2 V (u slučaju da igrač B odabere 1 strategiju dobitak igrača A treba biti veći od V) bx 1 + dx 2 V x 1 + x 2 = 1 (suma učestalosti svih varijabli odlučivanja je jednaka 1) x 1, x 2 0 V – slobodna varijabla D = V max! 50 x 1 + 75 x 2 + 50 x 3 + 25 x 4 ≥ V 25 x 1 + 50 x 2 + 60 x 3 + 70 x 4 ≥ V 50 x 1 + 40 x 2 + 50 x 3 + 80 x 4 ≥ V 75 x 1 + 30 x 2 + 20 x 3 + 50 x 4 ≥ V x 1 + x 2 + x 3 + x 4 = 1 x 1, 2, 3, 4 ≥ 0, V – slobodna varijabla Simplex metoda

Igrač B Druga tvrtka (Igrač B) Prva tvrtka (Igrač A) max Osijek Našice Đakovo Zagreb min Osijek 50% 25% 50% 75% 25% Našice 75% 50% 40% 30% Đakovo 50% 60% 50% 20% Zagreb 25% 70% 80% 50% 25% 70% 80% 75% D = V min – funkcija cilja (V je dobitak jednog, tj. gubitak drugog igrača, u ovom slučaju je V maksimalni gubitak koji se želi minimizirati) D = V min 50 y 1 + 25 y 2 + 50 y 3 + 75 y 4 ≤ V ay 1 + by 2 V (u slučaju da igrač A odabere 1 strategiju , gubitak igrača B ne smije biti veći od V) 75 y 1 + 50 y 2 + 40 y 3 + 30 y 4 ≤ V cy 1 + dy 2 V 25 y 1 + 70 y 2 + 80 y 3 + 50 y 4 ≤ V y 1 + y 2 = 1 (suma učestalosti svih varijabli odlučivanja je jednaka 1) y 1 + y 2 + y 3+ y 4 = 1 y 1, y 2 0 V – slobodna varijabla 50 y 1 + 60 y 2 + 50 y 3 + 20 y 4 ≤ V y 1, 2, 3, 4 ≥ 0, V – slobodna varijabla Simplex metoda

Rješenja: Zaključak: x 1 = 2/7 y 1 = 0 x 2 = 5/14 y 2 = 0 o igrač A (prva tvrtka) u 2/7 ( 28%) slučajeva bira strategiju x 1, tj. želi x 3 = 0 y 3 = 50/7 otvoriti predstavništvo u gradu x 4 = 5/14 y 4 = 0 Osijeku, v = 50 t 5 = 0 o u 5/14 ( 36%) slučajeva želi predstavništvo smjestiti u Našicama, D = 50 max! a tako i u Zagrebu D = V = 50 o za strategiju x 3 neće se odlučiti te neće predstavništvo smjestiti u grad Iščitavamo rješenja za igrača B problem Đakovo duala y 1 = 2/7 x 1 = 0 y 2 = 5/14 x 2 = 0 y 3 = 0 x 3 = 50/7 y 4 = 5/14 x 4 = 0 D = 50 min! v = 0 D = V = 50 o Primjenjujući ove strategije ostvarit će maksimalni dobitak od 50% osvojenog tržišta

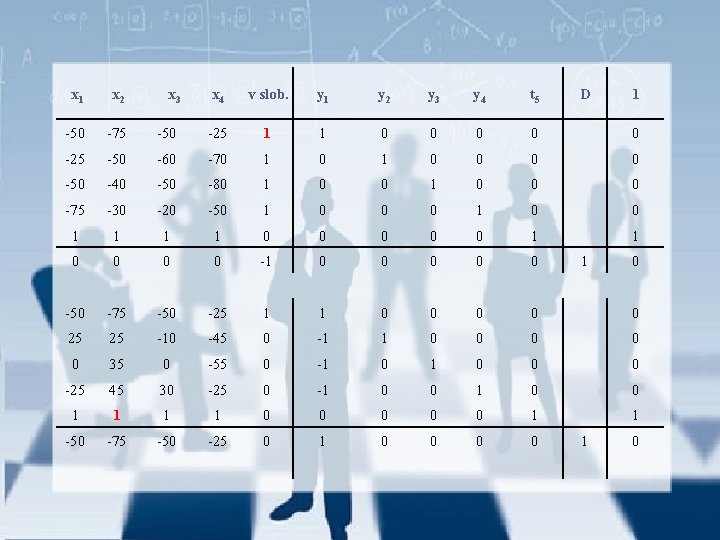
x 1 x 2 x 3 x 4 v slob. y 1 y 2 y 3 y 4 t 5 D 1 -50 -75 -50 -25 1 1 0 0 0 -25 -50 -60 -70 1 0 0 -50 -40 -50 -80 1 0 0 0 -75 -30 -20 -50 1 0 0 1 1 0 0 -1 0 0 0 1 0 -50 -75 -50 -25 1 1 0 0 0 25 25 -10 -45 0 -1 1 0 0 0 35 0 -55 0 -1 0 0 0 -25 45 30 -25 0 -1 0 0 1 1 0 0 0 1 1 -50 -75 -50 -25 0 1 0

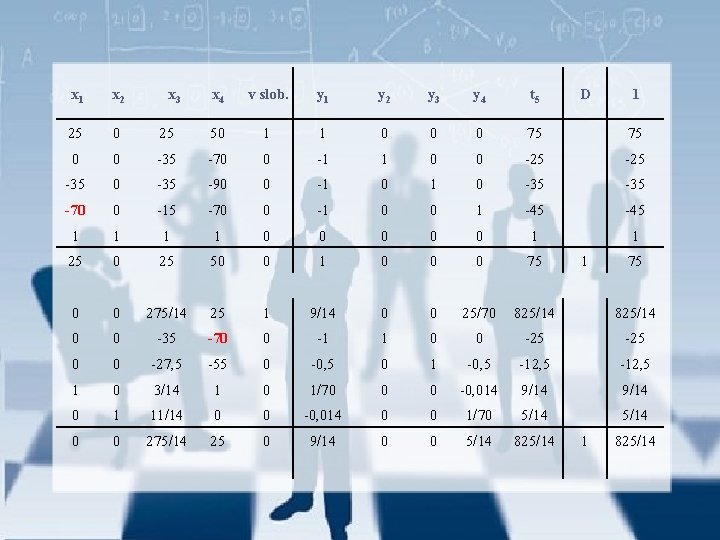
x 1 x 2 25 0 0 x 3 x 4 v slob. y 1 y 2 y 3 y 4 t 5 D 1 25 50 1 1 0 0 0 75 75 0 -35 -70 0 -1 1 0 0 -25 -35 0 -35 -90 0 -1 0 -35 -70 0 -15 -70 0 -1 0 0 1 -45 1 1 0 0 0 1 1 25 0 25 50 0 1 0 0 0 75 1 75 0 0 275/14 25 1 9/14 0 0 25/70 825/14 0 0 -35 -70 0 -1 1 0 0 -25 0 0 -27, 5 -55 0 -0, 5 0 1 -0, 5 -12, 5 1 0 3/14 1 0 1/70 0 0 -0, 014 9/14 0 1 11/14 0 0 -0, 014 0 0 1/70 5/14 0 0 275/14 25 0 9/14 0 0 5/14 825/14 1 825/14

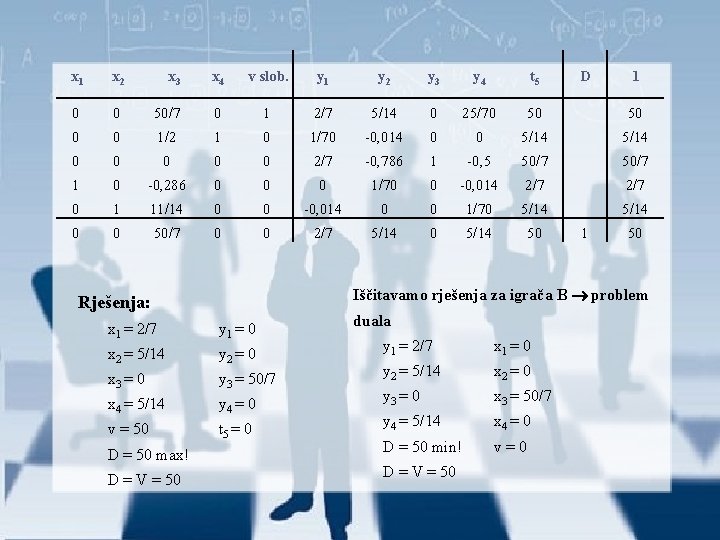
x 1 x 2 x 3 x 4 v slob. y 1 y 2 y 3 y 4 t 5 0 0 50/7 0 1 2/7 5/14 0 25/70 50 50 0 0 1/2 1 0 1/70 -0, 014 0 0 5/14 0 0 0 2/7 -0, 786 1 -0, 5 50/7 1 0 -0, 286 0 0 0 1/70 0 -0, 014 2/7 0 1 11/14 0 0 -0, 014 0 0 1/70 5/14 0 0 50/7 0 0 2/7 5/14 0 5/14 50 Rješenja: 1 1 50 Iščitavamo rješenja za igrača B problem duala y 1 = 0 y 1 = 2/7 x 1 = 0 x 2 = 5/14 y 2 = 0 y 2 = 5/14 x 2 = 0 x 3 = 0 y 3 = 50/7 y 3 = 0 x 3 = 50/7 x 4 = 5/14 y 4 = 0 y 4 = 5/14 x 4 = 0 v = 50 t 5 = 0 D = 50 min! v = 0 D = 50 max! D = V = 50 x 1 = 2/7 D

Rješenja: Zaključak: x 1 = 2/7 y 1 = 0 x 2 = 5/14 y 2 = 0 o igrač A (prva tvrtka) u 2/7 ( 28%) slučajeva bira strategiju x 1, tj. želi x 3 = 0 y 3 = 50/7 otvoriti predstavništvo u gradu x 4 = 5/14 y 4 = 0 Osijeku, v = 50 t 5 = 0 o u 5/14 ( 36%) slučajeva želi predstavništvo smjestiti u Našicama, D = 50 max! a tako i u Zagrebu D = V = 50 o za strategiju x 3 neće se odlučiti te neće predstavništvo smjestiti u grad Iščitavamo rješenja za igrača B problem Đakovo duala y 1 = 2/7 x 1 = 0 y 2 = 5/14 x 2 = 0 y 3 = 0 x 3 = 50/7 y 4 = 5/14 x 4 = 0 D = 50 min! v = 0 D = V = 50 o Primjenjujući ove strategije ostvarit će maksimalni dobitak od 50% osvojenog tržišta

IGRE PROTIV PRIRODE Priroda neracionalna pojava, koja ne vodi računa i nema interes za ishode igre o Čovjek (Igrač) inteligentan o Igra između prirode i čovjeka igrač igra svoju najbolju strategiju i pri tome je posve indiferentan prema prirodi o Različiti pristupi rješavanja (kriteriji): a) Laplace b) Hurwicz c) Savage o

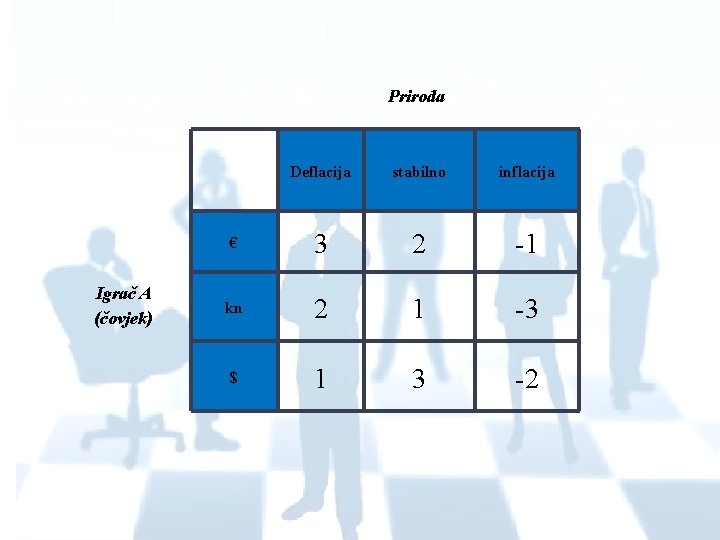
ZADATAK… 1. Međunarodna tvrtka, iz našeg prošlog primjera, odlučila je otvoriti predstavništvo svoje tvrtke u Hrvatskoj, u gradu Zagrebu. Za otvaranje predstavništva, treba joj dodatnih financijskih sredstava, te se ona odlučila na podizanje kredita. Ona ima mogućnost podići kredit u eurima, američkim dolarima i kunama. Prilikom podizanja kredita zanima ju koja joj je mogućnost, odnosno strategija najbolja u optimalnom smislu, u slučajevima inflacije, deflacije i stabilnog stanja koji se mogu pojaviti u Hrvatskoj kao posljedica njenog i svjetskog gospodarstva i bankarstva te funkcioniranja tržišta uopće.

Priroda Igrač A (čovjek) Deflacija stabilno inflacija € 3 2 -1 kn 2 1 -3 $ 1 3 -2

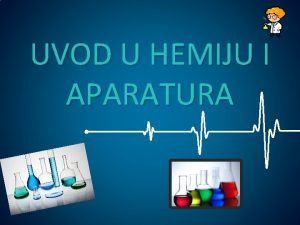
LAPLACEOV KRITERIJ o Pretpostavka: sve su vjerojatnosti jednake (nema ih četiri, nego samo jedna) pa nema razloga za preferenciju bilo koje opcije prirode nakon izračunavanja izabire se red s najvećom vrijednosti pa je ta strategija optimalna strategija za igrača

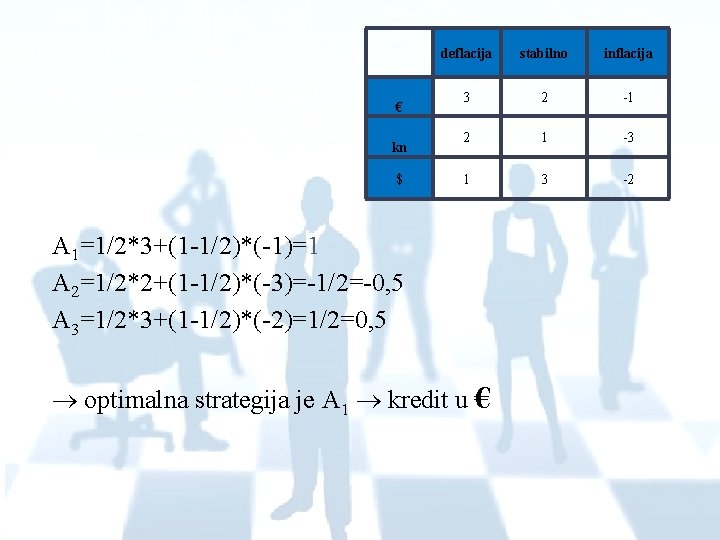
maxi [ 1/n*ai 1 + 1/n*ai 2+…+ 1/n*ain ] A 1=1/3*3+1/3*2+1/3*(-1)=4/3=1, 33 A 2=1/3*2+1/3*1+1/3*(-3)=0 A 3=1/3*1+1/3*3+1/3*(-2)=2/3=0, 67 optimalna strategija je A 1 kredit u € Deflacija stabilno inflacija € 3 2 -1 kn 2 1 -3 $ 1 3 -2

HURWICZOV KRITERIJ � Optimizam igrača se izražava brojem α tako da je 0 ≤ ≤ 1 ako je dobiveni rezultat u nekoj od strategija bliže jedinici- više nam je stalo do prirode, a ako je bliže nuli – manje nam je stalo do reakcije prirode Hurwiczov kriterij uključuje maksimum u obliku specijalnog slučaja: - potrebno je odabrati koeficijent optimizma – označen kao α pa se izračuna po formuli: � α *(max. reda) + (1 - α)* (min. reda) te odabrati red koji daje maksimalni iznos

€ kn $ deflacija stabilno inflacija 3 2 -1 2 1 -3 1 3 -2 A 1=1/2*3+(1 -1/2)*(-1)=1 A 2=1/2*2+(1 -1/2)*(-3)=-1/2=-0, 5 A 3=1/2*3+(1 -1/2)*(-2)=1/2=0, 5 optimalna strategija je A 1 kredit u €

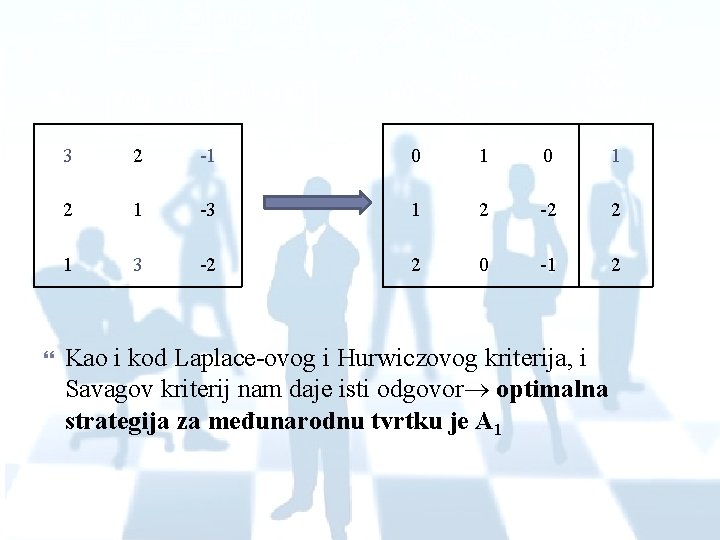
SAVAGEOV KRITERIJ matrica žaljenja 1. Izračunamo matricu za svaku opciju i odabiremo onu kod koje će maksimalno žaljenje za opcijom biti najmanje 2. Radimo redukciju matrice po stupcu tako da pronađemo najveći element svakog stupca i od njega oduzmemo sve ostale elemente stupca i njega samog od sebe 3. Pronalazimo najveći element svakog reda i minimalni od tih maksimalnih elemenata odabiremo kao optimalnu strategiju za igrača

3 2 -1 0 1 2 1 -3 1 2 -2 2 1 3 -2 2 0 -1 2 Kao i kod Laplace-ovog i Hurwiczovog kriterija, i Savagov kriterij nam daje isti odgovor optimalna strategija za međunarodnu tvrtku je A 1

- Primjena teorije igara o o o o u ekonomiji, političkim znanostima, operacijskim istraživanjima, računarstvu, sportu, vojnoj strategiji, te bilo kojem sustavu sa određenim pravilima.

- Praktična primjena u poslovanju o Cjenovna konkurencija određivanja cijena - o Neprijateljsko preuzimanje poduzeća vs. prijateljsko spajanje Sprječavanje ulaska na tržište – npr. prijetnja sindikata štrajkom o komplicirane sheme

- Primjena u društvenim znanostima Pravo o o radno zakonska regulativa vezana uz zaštitu okoliša pregovaranje i parničenje ugovorno Političke znanosti o o primjer terorizma pravedna podjela, politička ekonomija, teorija javnog izbora, pozitivna politička teorija, teorija društvenog izbora, sukobi i ratno pregovaranje i međunarodni odnosi

- Teorija igara u međunarodnoj ekonomiji o o strateška međuovisnost stvaranje carinskih unija, pregovori o smanjenu carina, korištenje resursa međunarodne zajedničke imovine, kartelski sporazumi i dr.

- Marketing – odlučivanje temeljeno na teoriji igre o o Reklamiranje proizvoda – npr. konkurentska “borba” kroz reklamnu kampanju Pogrešna odluka značajni gubici