Shortest Paths and Minimum Spanning Trees David Kauchak

Shortest Paths and Minimum Spanning Trees David Kauchak cs 302 Spring 2013

Admin Can resubmit homeworks 12 -15 for up to half credit back l Due by the end of the week Read book

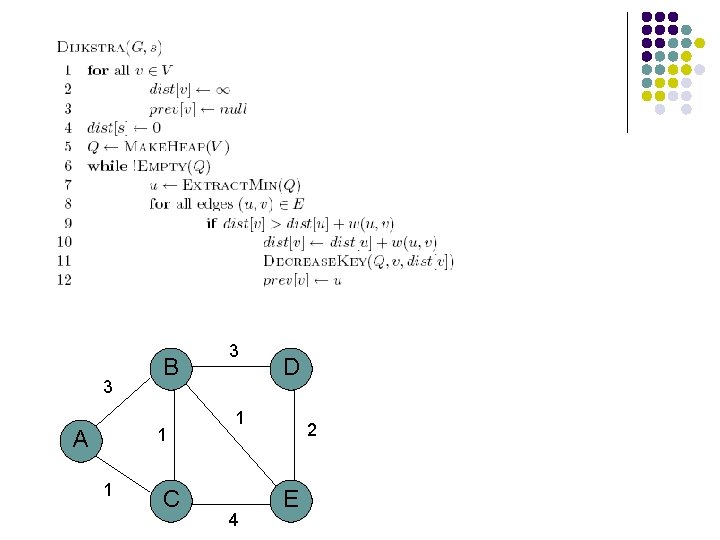
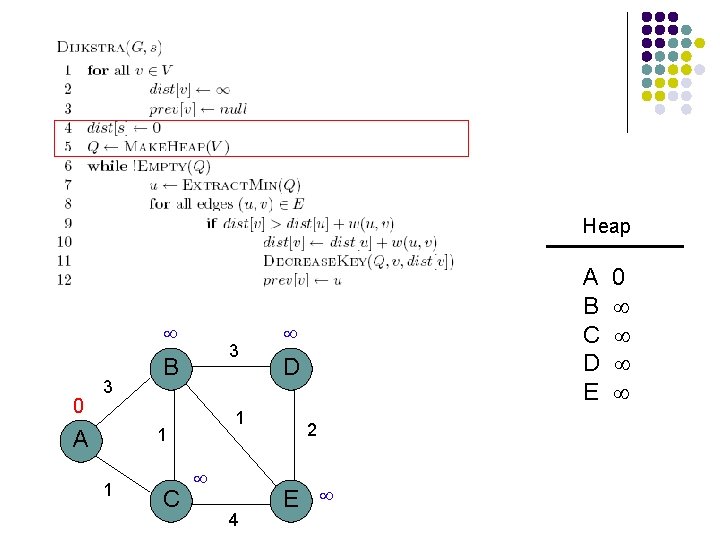
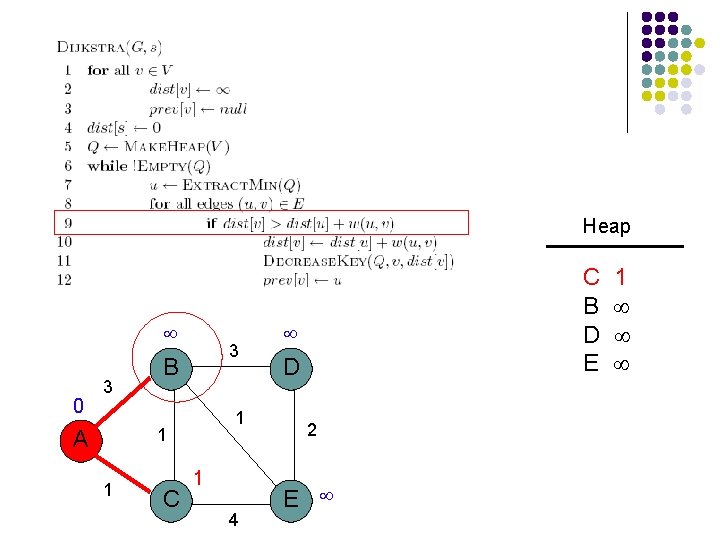
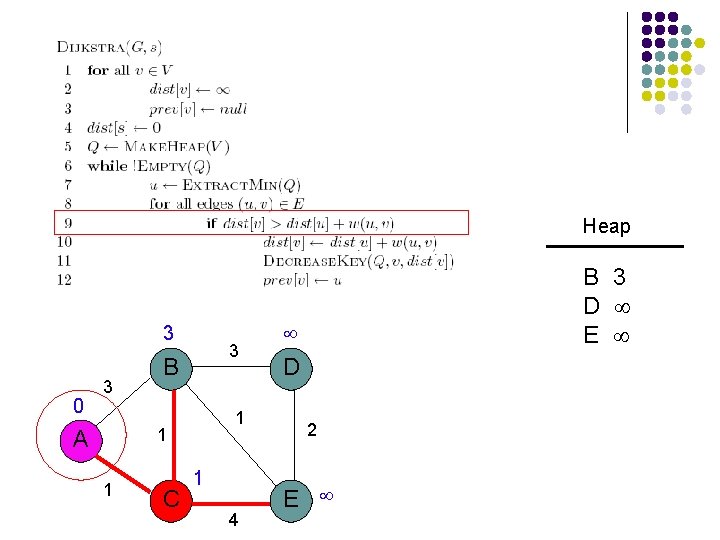
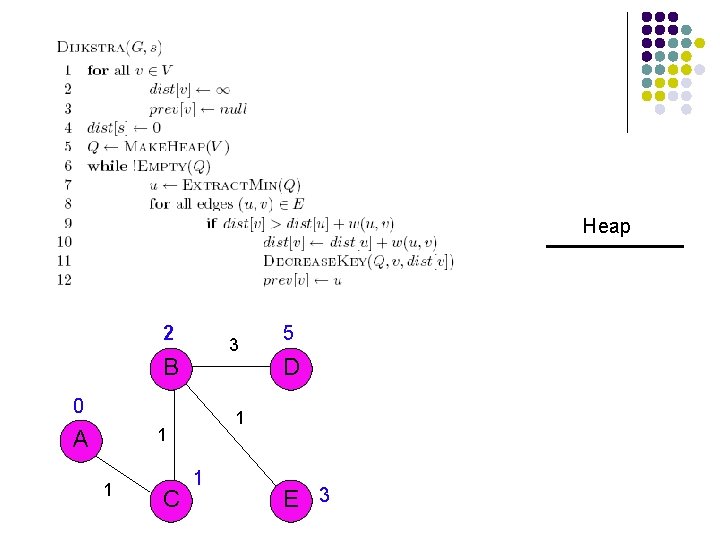
3 B 1 A 1 C 3 D 1 4 2 E

3 3 B 1 1 A 1 C 4 D 2 E

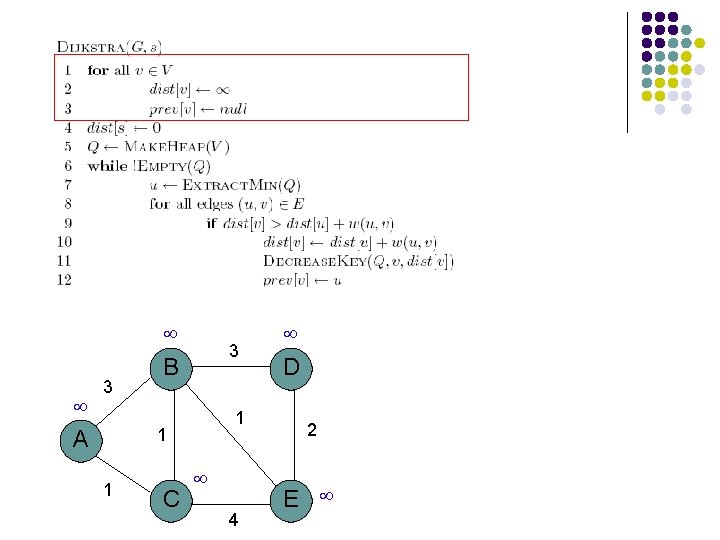
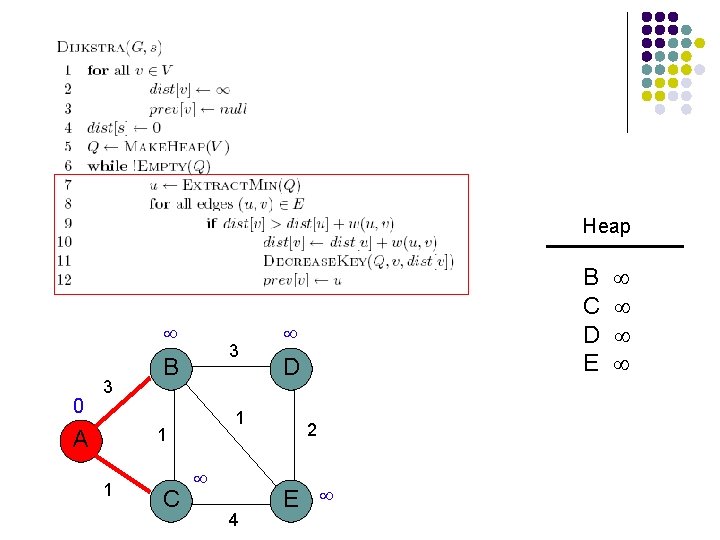
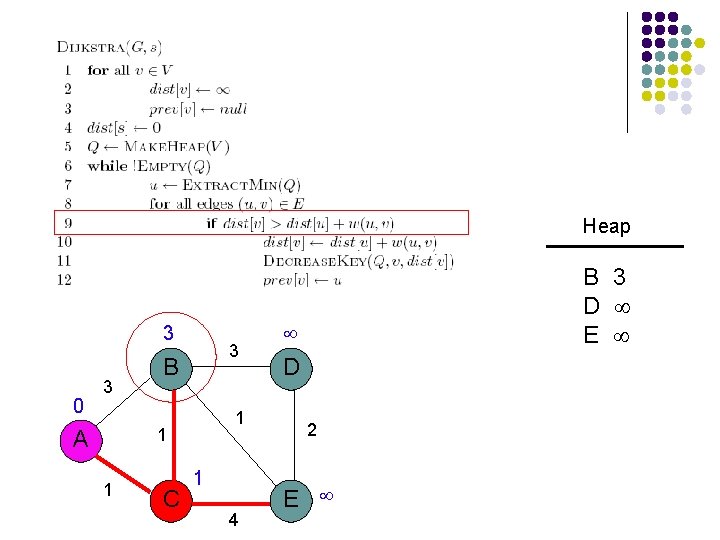
Heap 0 3 3 B 1 1 A 1 C 4 A B C D E D 2 E 0

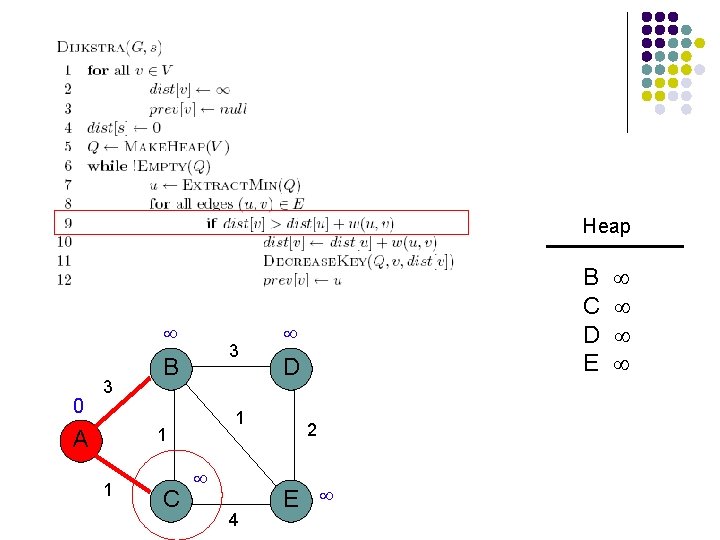
Heap 0 3 3 B 1 1 A 1 C 4 B C D E D 2 E

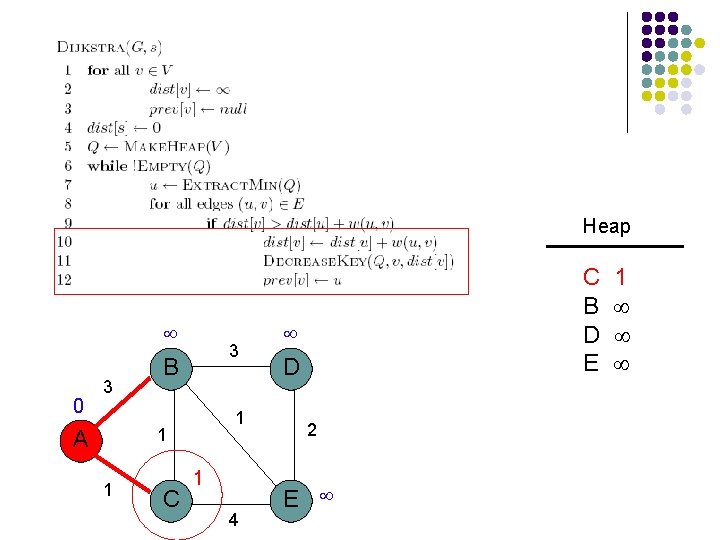
Heap 0 3 3 B 1 1 A 1 C 4 B C D E D 2 E

Heap 0 3 3 B 1 1 A 1 C 1 4 C B D E D 2 E 1

Heap 0 3 3 B 1 1 A 1 C 1 4 C B D E D 2 E 1

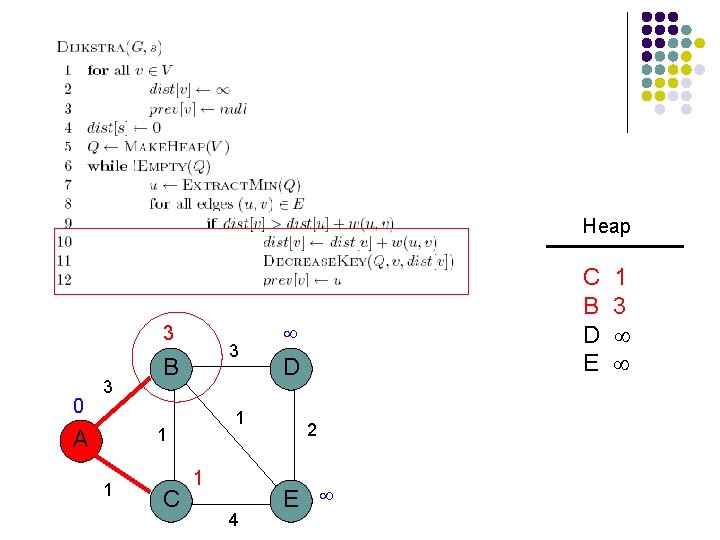
Heap 3 0 3 3 B 1 1 A 1 C 1 4 C B D E D 2 E 1 3

Heap 3 0 3 3 B 1 1 A 1 C 1 4 C B D E D 2 E 1 3

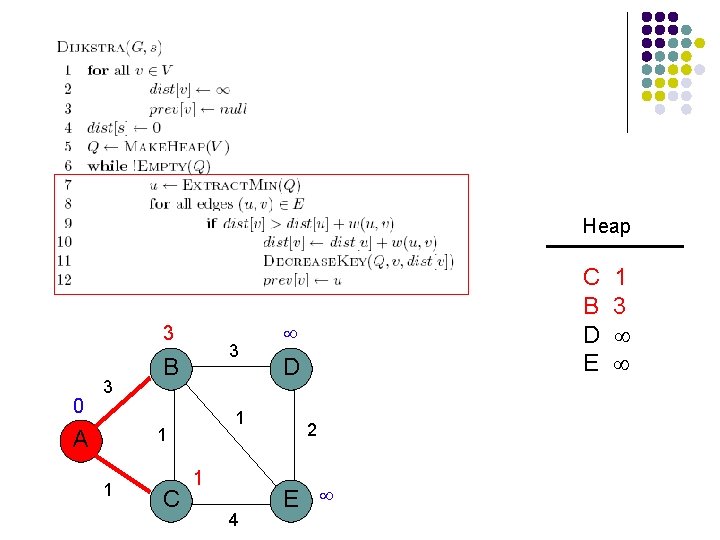
Heap 3 0 3 3 B 1 1 A 1 C 1 4 B 3 D E D 2 E

Heap 3 0 3 3 B 1 1 A 1 C 1 4 B 3 D E D 2 E

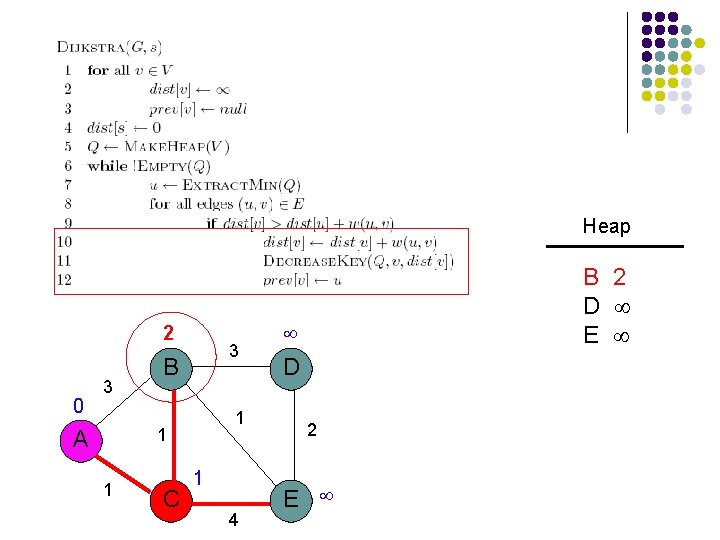
Heap 3 0 3 3 B 1 1 A 1 C 1 4 B 3 D E D 2 E

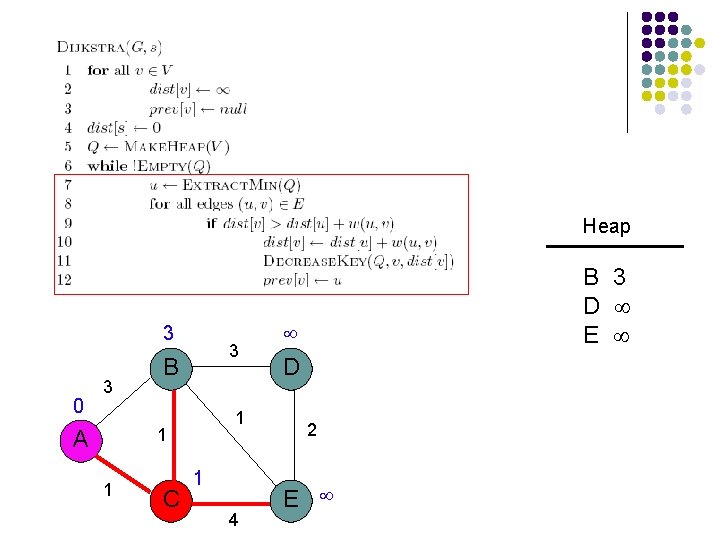
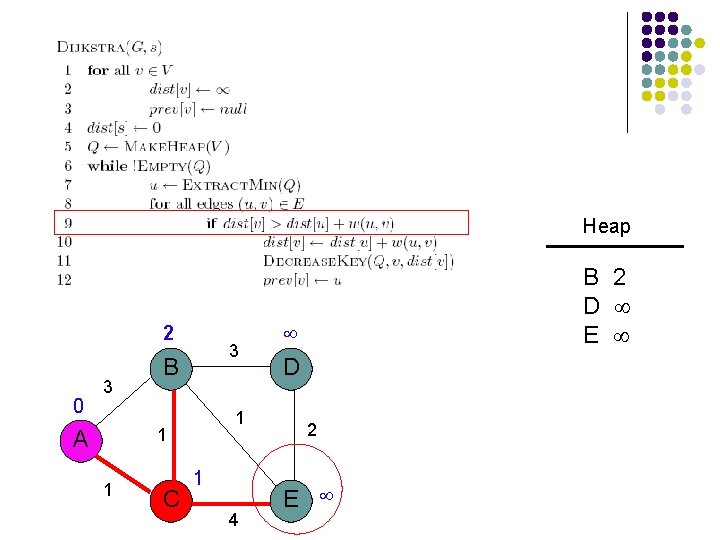
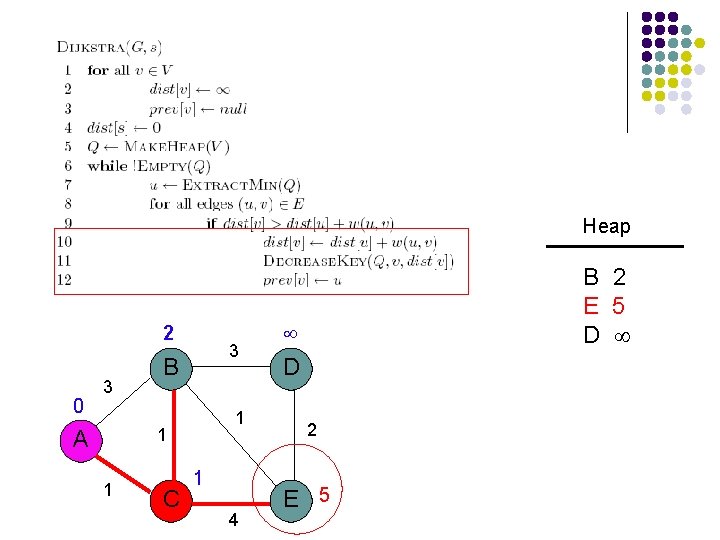
Heap 2 0 3 3 B 1 1 A 1 C 1 4 B 2 D E D 2 E

Heap 2 0 3 3 B 1 1 A 1 C 1 4 B 2 D E D 2 E

Heap 2 0 3 3 B 1 1 A 1 C 1 4 B 2 E 5 D D 2 E 5

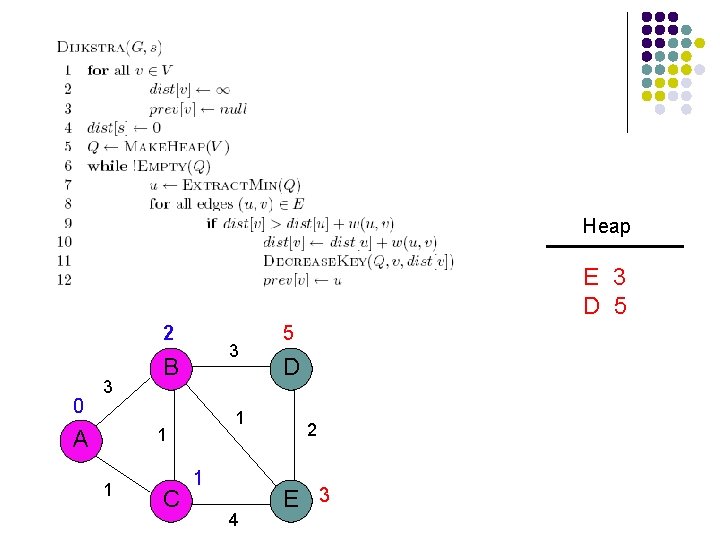
Heap E 3 D 5 2 0 3 3 B 1 1 A 1 C 1 4 5 D 2 E 3

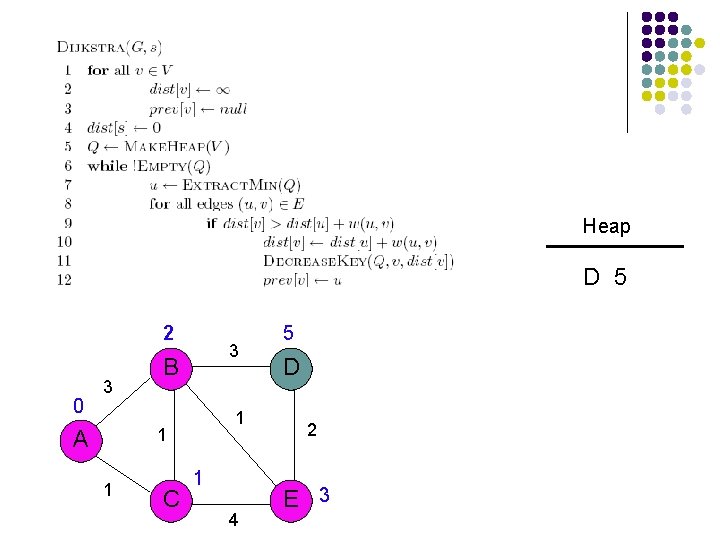
Heap D 5 2 0 3 3 B 1 1 A 1 C 1 4 5 D 2 E 3

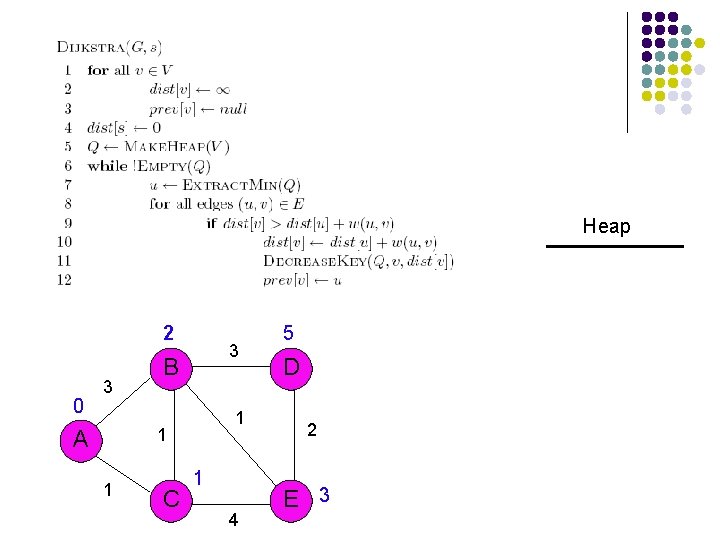
Heap 2 0 3 3 B 1 1 A 1 C 1 4 5 D 2 E 3

Heap 2 3 B 0 1 C D 1 1 A 5 1 E 3

Is Dijkstra’s algorithm correct? Invariant:

Is Dijkstra’s algorithm correct? Invariant: For every vertex removed from the heap, dist[v] is the actual shortest distance from s to v proof?

Is Dijkstra’s algorithm correct? Invariant: For every vertex removed from the heap, dist[v] is the actual shortest distance from s to v l The only time a vertex gets visited is when the distance from s to that vertex is smaller than the distance to any remaining vertex l Therefore, there cannot be any other path that hasn’t been visited already that would result in a shorter path

Running time?

Running time? 1 call to Make. Heap

Running time? |V| iterations

Running time? |V| calls

Running time? O(|E|) calls

Running time? Depends on the heap implementation 1 Make. Heap |V| Extract. Min |E| Decrease. Key Array O(|V|) O(|V|2) O(|E|) Bin heap O(|V|) O(|V| log |V|) O(|E| log |V|) Total O(|V|2) O((|V|+|E|) log |V|) O(|E| log |V|)

Running time? Depends on the heap implementation 1 Make. Heap |V| Extract. Min |E| Decrease. Key Array O(|V|) O(|V|2) O(|E|) Bin heap O(|V|) O(|V| log |V|) O(|E| log |V|) Total O(|V|2) O((|V|+|E|) log |V|) O(|E| log |V|) Is this an improvement? If |E| < |V|2 / log |V|

Running time? Depends on the heap implementation 1 Make. Heap |V| Extract. Min |E| Decrease. Key Array O(|V|) O(|V|2) O(|E|) Bin heap O(|V|) O(|V| log |V|) O(|E| log |V|) Total O(|V|2) O((|V|+|E|) log |V|) O(|E| log |V|) Fib heap O(|V|) O(|V| log |V|) O(|E|) O(|V| log |V| + |E|)

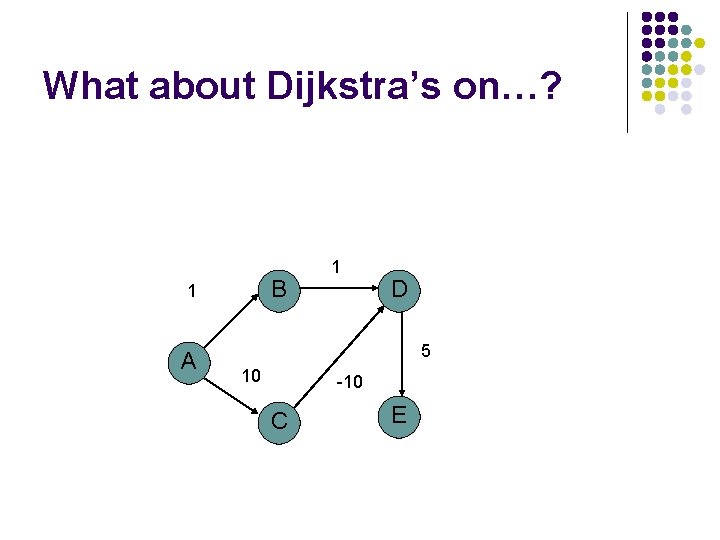
What about Dijkstra’s on…? B 1 A 1 D 5 10 -10 C E

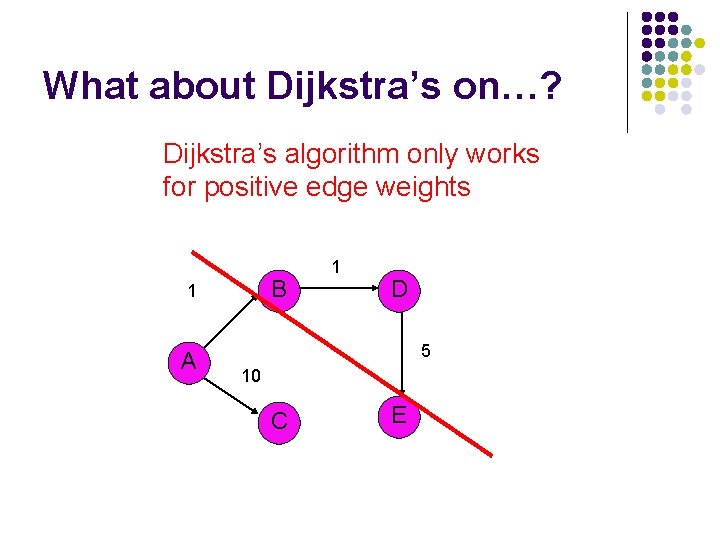
What about Dijkstra’s on…? Dijkstra’s algorithm only works for positive edge weights B 1 A 1 D 5 10 C E

Bounding the distance Another invariant: For each vertex v, dist[v] is an upper bound on the actual shortest distance Is this a valid invariant?

Bounding the distance Another invariant: For each vertex v, dist[v] is an upper bound on the actual shortest distance l l start off at only update the value if we find a shorter distance An update procedure

Can we ever go wrong applying this update rule? l We can apply this rule as many times as we want and will never underestimate dist[v] When will dist[v] be right? l If u is along the shortest path to v and dist[u] is correct

dist[v] will be right if u is along the shortest path to v and dist[u] is correct Consider the shortest path from s to v s p 1 p 2 p 3 pk v

dist[v] will be right if u is along the shortest path to v and dist[u] is correct What happens if we update all of the vertices with the above update? s p 1 p 2 p 3 pk v

dist[v] will be right if u is along the shortest path to v and dist[u] is correct What happens if we update all of the vertices with the above update? s correct p 1 p 2 p 3 pk v

dist[v] will be right if u is along the shortest path to v and dist[u] is correct What happens if we update all of the vertices with the above update? s p 1 correct p 2 p 3 pk v

dist[v] will be right if u is along the shortest path to v and dist[u] is correct Does the order that we update the vertices matter? s p 1 correct p 2 p 3 pk v

dist[v] will be right if u is along the shortest path to v and dist[u] is correct How many times do we have to do this for vertex pi to have the correct shortest path from s? l s i times p 1 p 2 p 3 pk v

dist[v] will be right if u is along the shortest path to v and dist[u] is correct How many times do we have to do this for vertex pi to have the correct shortest path from s? l i times s p 1 correct p 2 p 3 pk v

dist[v] will be right if u is along the shortest path to v and dist[u] is correct How many times do we have to do this for vertex pi to have the correct shortest path from s? l i times s p 1 p 2 correct p 3 pk v

dist[v] will be right if u is along the shortest path to v and dist[u] is correct How many times do we have to do this for vertex pi to have the correct shortest path from s? l i times s p 1 correct p 2 p 3 correct pk v

dist[v] will be right if u is along the shortest path to v and dist[u] is correct How many times do we have to do this for vertex pi to have the correct shortest path from s? l i times s p 1 correct p 2 p 3 correct pk … v

dist[v] will be right if u is along the shortest path to v and dist[u] is correct What is the longest (vertex-wise) the path from s to any node v can be? l |V| - 1 edges/vertices s p 1 correct p 2 p 3 correct pk … v

Bellman-Ford algorithm

Bellman-Ford algorithm Initialize all the distances do it |V| -1 times iterate over all edges/vertices and apply update rule

Bellman-Ford algorithm check for negative cycles

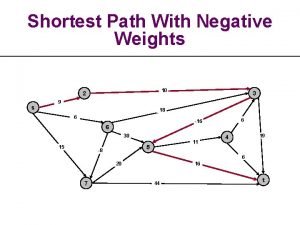
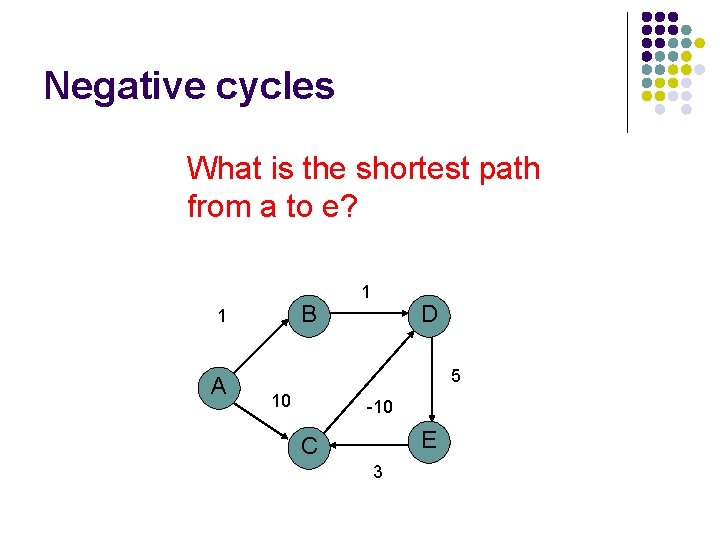
Negative cycles What is the shortest path from a to e? B 1 A 1 D 5 10 -10 E C 3

Bellman-Ford algorithm

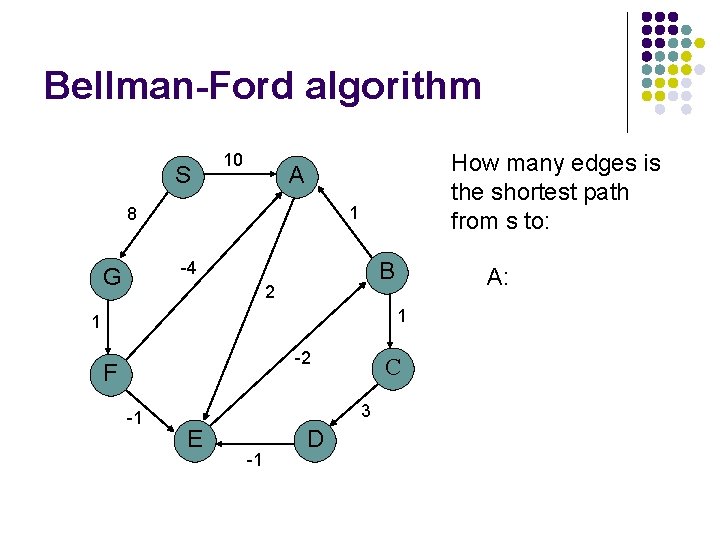
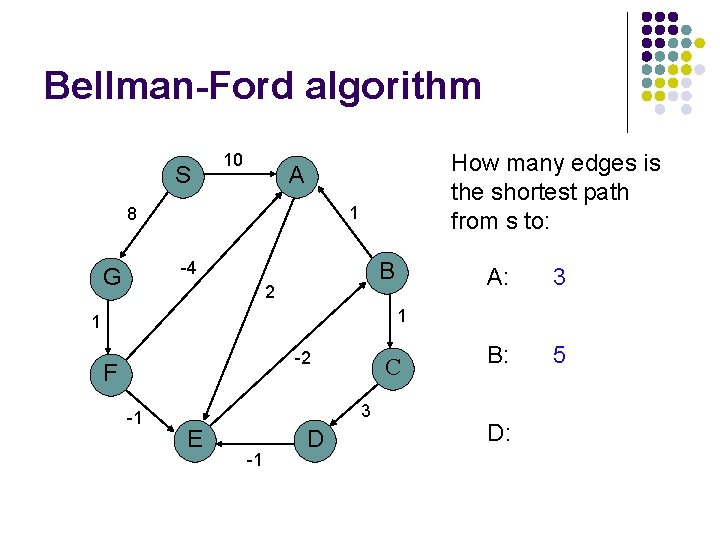
Bellman-Ford algorithm S 10 How many edges is the shortest path from s to: A 1 8 B -4 G 2 A: 1 1 -2 F -1 C 3 E -1 D

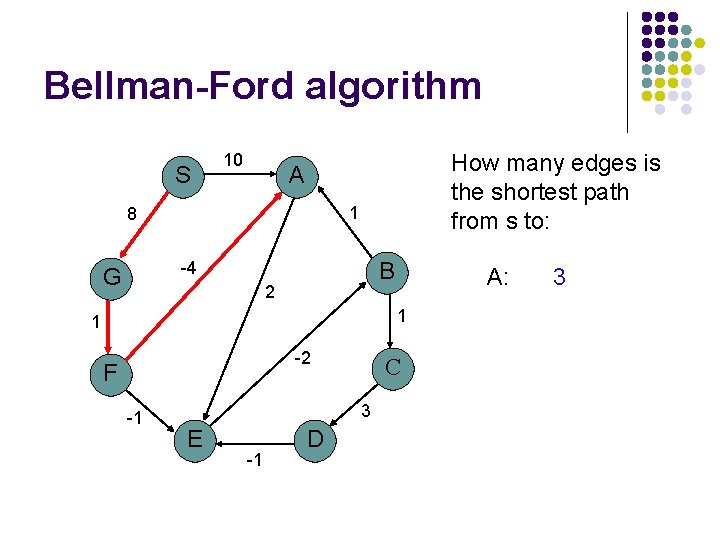
Bellman-Ford algorithm S 10 How many edges is the shortest path from s to: A 1 8 B -4 G 2 A: 1 1 -2 F -1 C 3 E -1 D 3

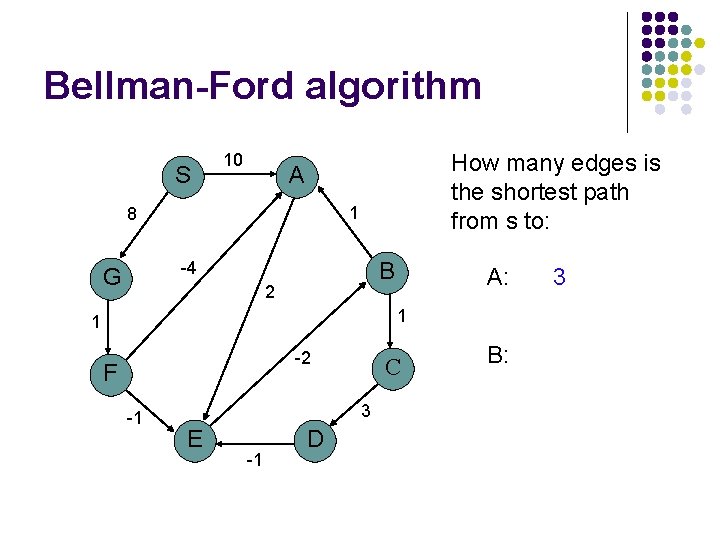
Bellman-Ford algorithm S 10 How many edges is the shortest path from s to: A 1 8 B -4 G 2 A: 1 1 -2 F -1 C 3 E -1 D B: 3

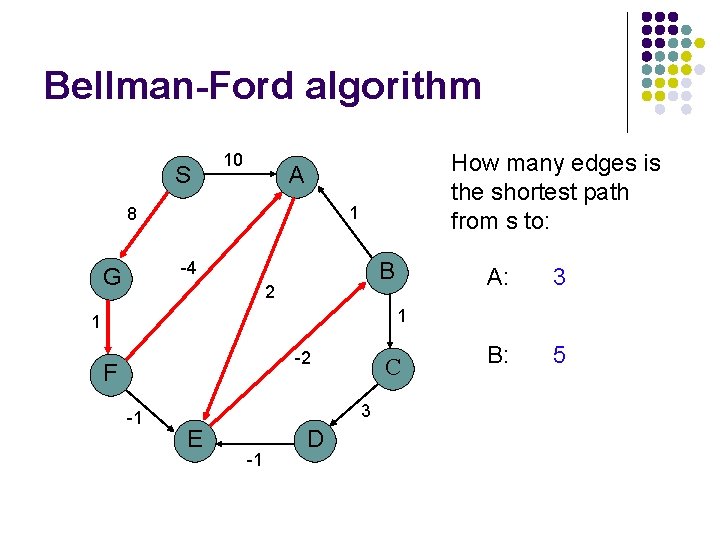
Bellman-Ford algorithm S 10 How many edges is the shortest path from s to: A 1 8 B -4 G 2 A: 3 B: 5 1 1 -2 F -1 C 3 E -1 D

Bellman-Ford algorithm S 10 How many edges is the shortest path from s to: A 1 8 B -4 G 2 A: 3 B: 5 1 1 -2 F -1 C 3 E -1 D D:

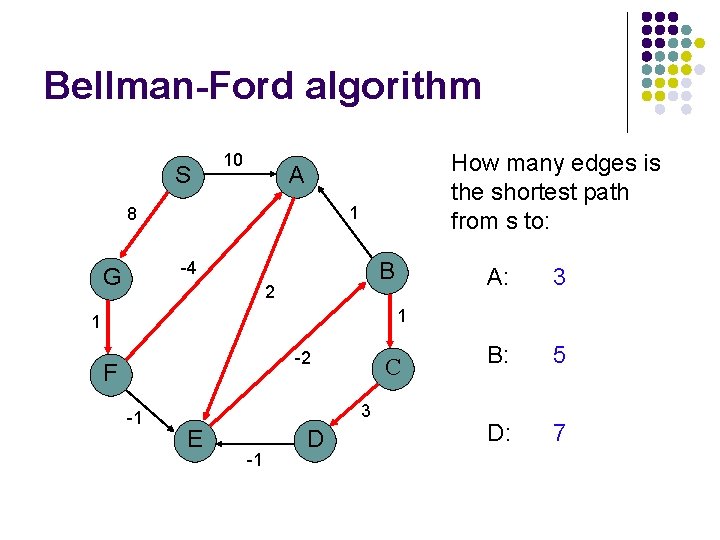
Bellman-Ford algorithm S 10 How many edges is the shortest path from s to: A 1 8 B -4 G 2 A: 3 B: 5 D: 7 1 1 -2 F -1 C 3 E -1 D

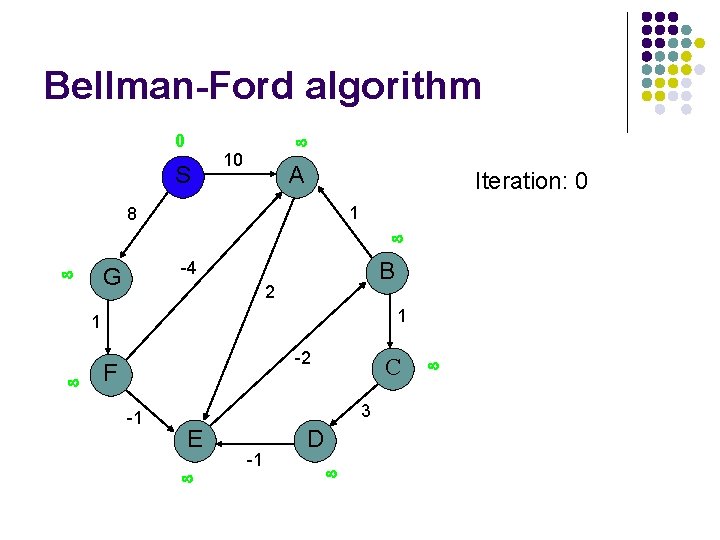
Bellman-Ford algorithm 0 S 10 A Iteration: 0 1 8 B -4 G 2 1 1 -2 F -1 C 3 E -1 D

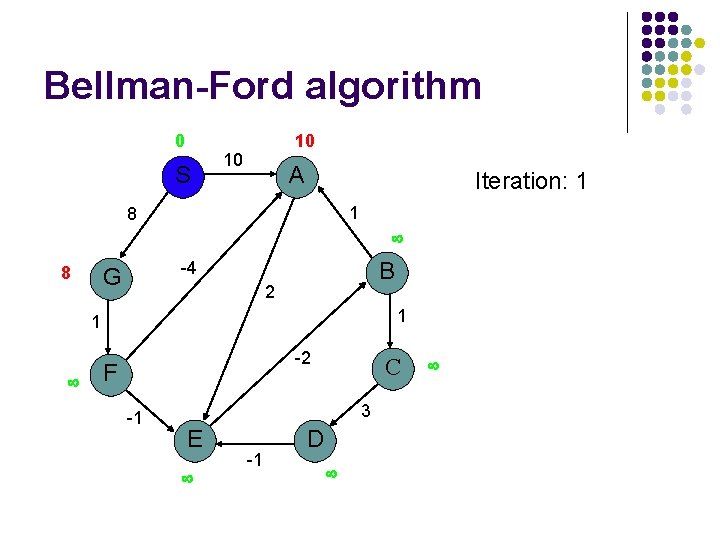
Bellman-Ford algorithm 0 S 10 10 A Iteration: 1 1 8 8 B -4 G 2 1 1 -2 F -1 C 3 E -1 D

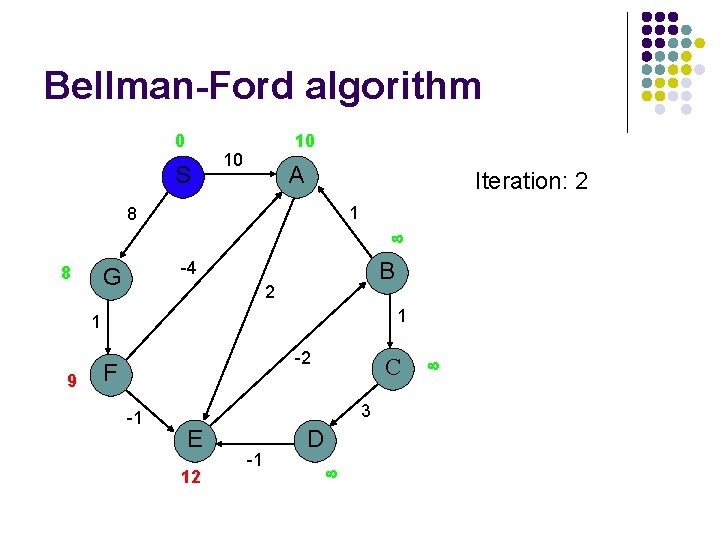
Bellman-Ford algorithm 0 S 10 10 A Iteration: 2 1 8 8 B -4 G 2 1 1 9 -2 F -1 C 3 E 12 -1 D

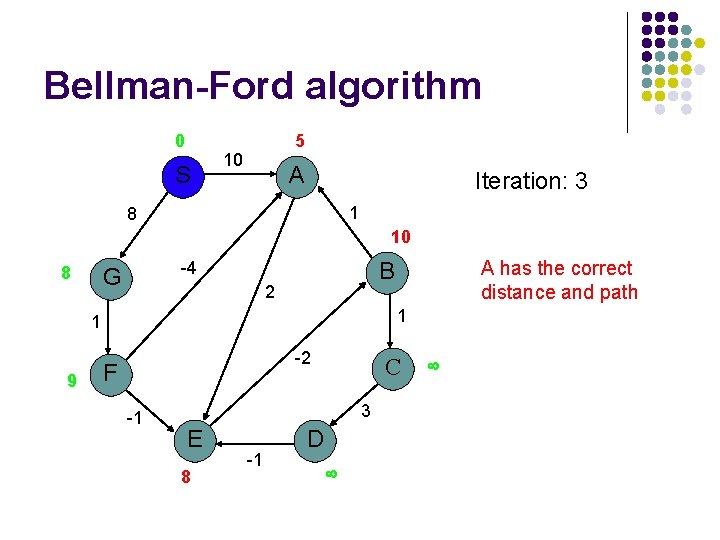
Bellman-Ford algorithm 0 S 5 10 A Iteration: 3 1 8 10 8 2 1 1 9 A has the correct distance and path B -4 G -2 F -1 C 3 E 8 -1 D

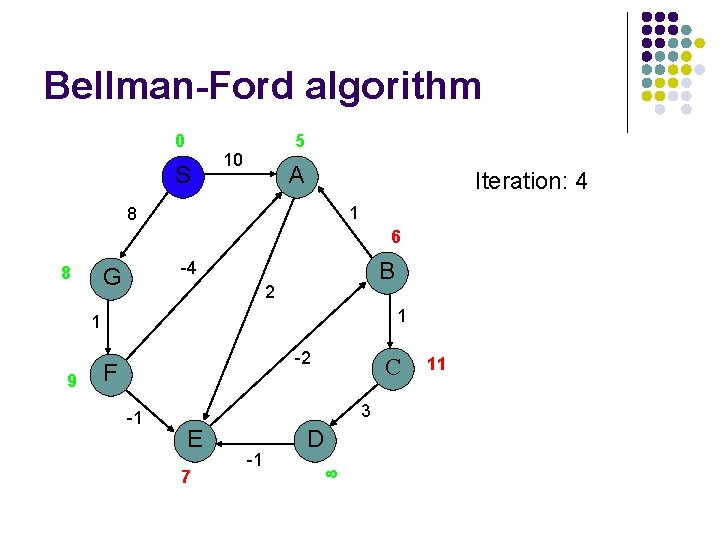
Bellman-Ford algorithm 0 S 5 10 A Iteration: 4 1 8 6 8 B -4 G 2 1 1 9 -2 F -1 C 3 E 7 -1 D 11

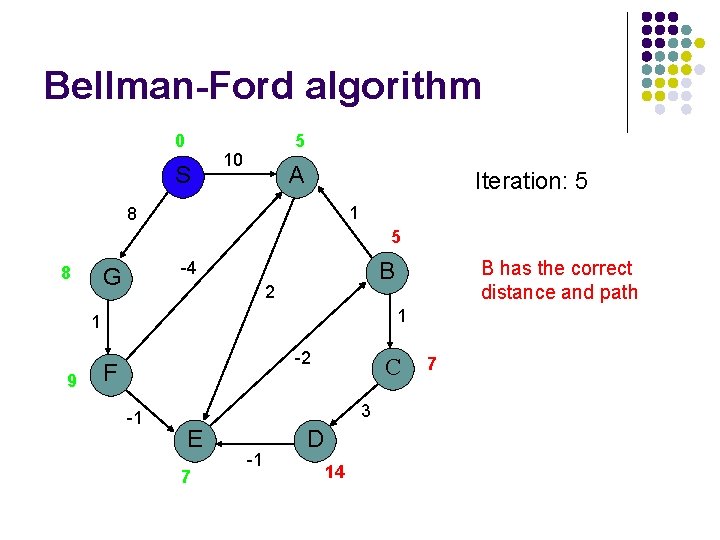
Bellman-Ford algorithm 0 S 5 10 A Iteration: 5 1 8 5 8 2 1 1 9 B has the correct distance and path B -4 G -2 F -1 C 3 E 7 -1 D 14 7

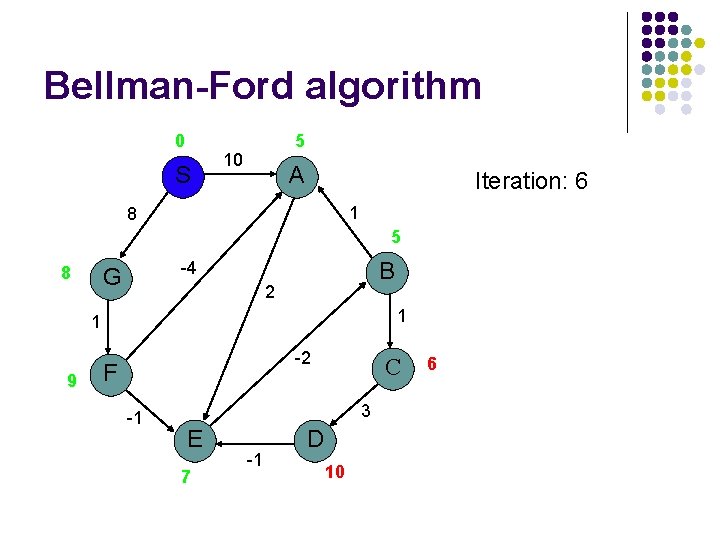
Bellman-Ford algorithm 0 S 5 10 A Iteration: 6 1 8 5 8 B -4 G 2 1 1 9 -2 F -1 C 3 E 7 -1 D 10 6

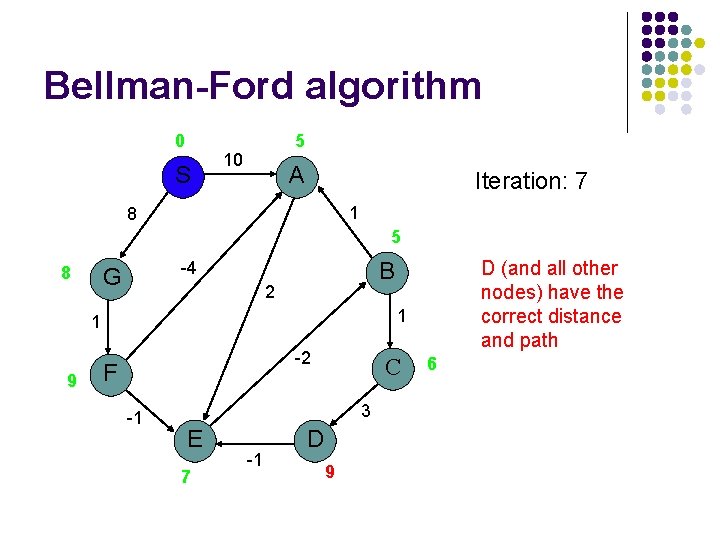
Bellman-Ford algorithm 0 S 5 10 A Iteration: 7 1 8 5 8 2 1 1 9 D (and all other nodes) have the correct distance and path B -4 G -2 F -1 C 3 E 7 -1 D 9 6

Correctness of Bellman-Ford Loop invariant:

Correctness of Bellman-Ford Loop invariant: After iteration i, all vertices with shortest paths from s of length i edges or less have correct distances

Runtime of Bellman-Ford O(|V| |E|)

Runtime of Bellman-Ford Can you modify the algorithm to run faster (in some circumstances)?

Single source shortest paths All of the shortest path algorithms we’ve looked at today are call “single source shortest paths” algorithms Why?

All pairs shortest paths Simple approach l l Call Bellman-Ford |V| times O(|V|2 |E|) Floyd-Warshall – Θ(|V|3) Johnson’s algorithm – O(|V|2 log |V| + |V| |E|)

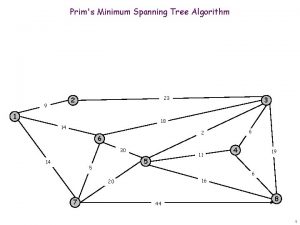
Minimum spanning trees What is the lowest weight set of edges that connects all vertices of an undirected graph with positive weights Input: An undirected, positive weight graph, G=(V, E) Output: A tree T=(V, E’) where E’ E that minimizes

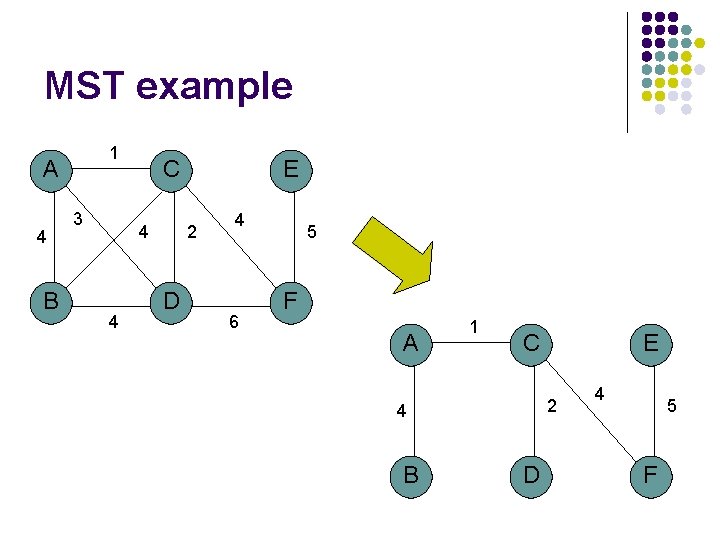
MST example 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F A 1 C 2 4 B E D 4 5 F

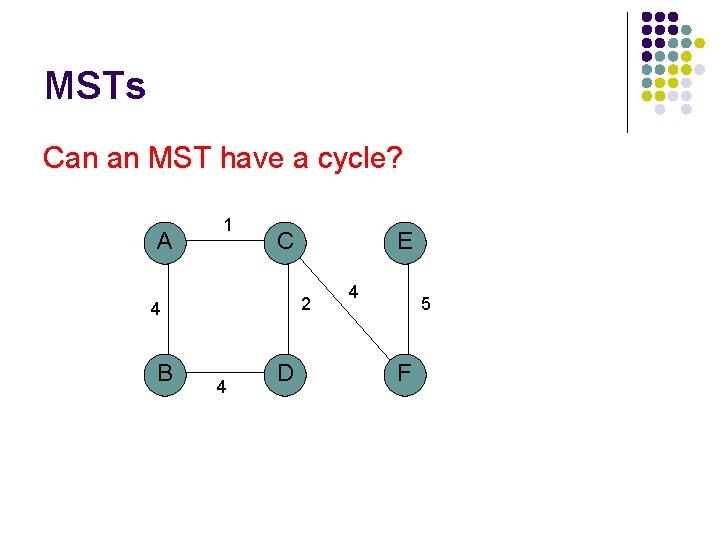
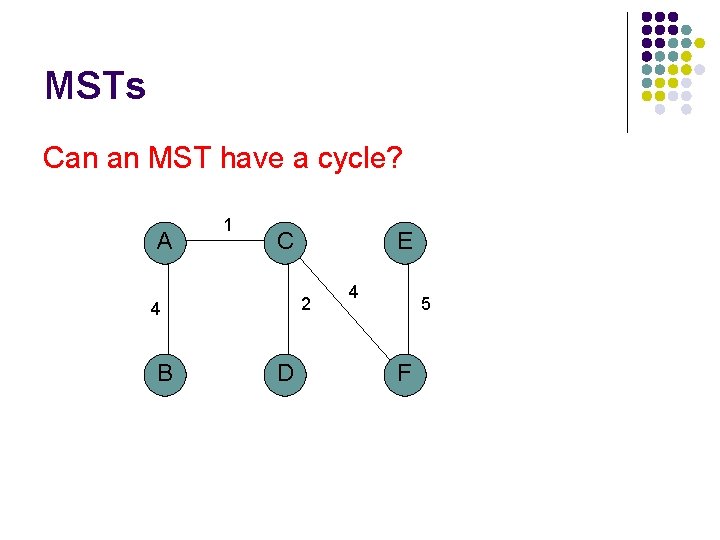
MSTs Can an MST have a cycle? A 1 C 2 4 B E 4 D 4 5 F

MSTs Can an MST have a cycle? A 1 C 2 4 B E D 4 5 F

Applications? Connectivity l l Networks (e. g. communications) Circuit design/wiring hub/spoke models (e. g. flights, transportation) Traveling salesman problem?

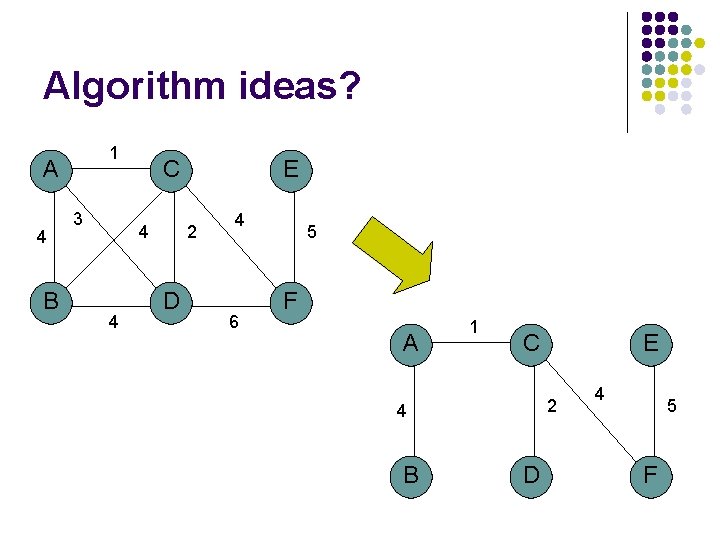
Algorithm ideas? 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F A 1 C 2 4 B E D 4 5 F

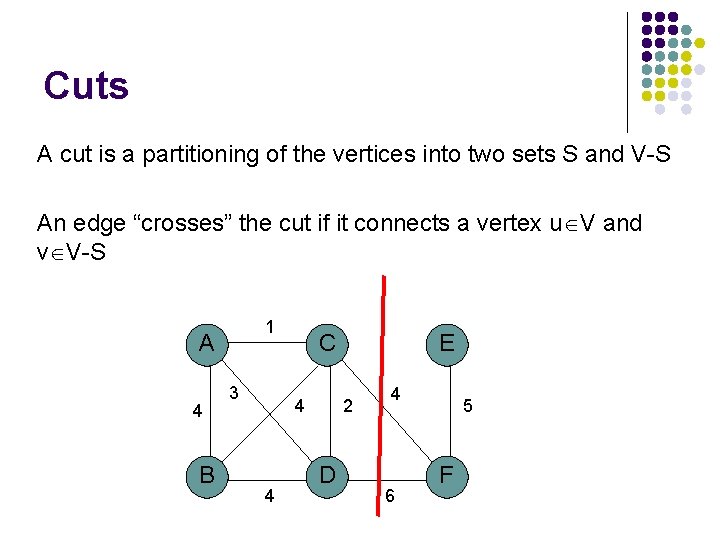
Cuts A cut is a partitioning of the vertices into two sets S and V-S An edge “crosses” the cut if it connects a vertex u V and v V-S 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F

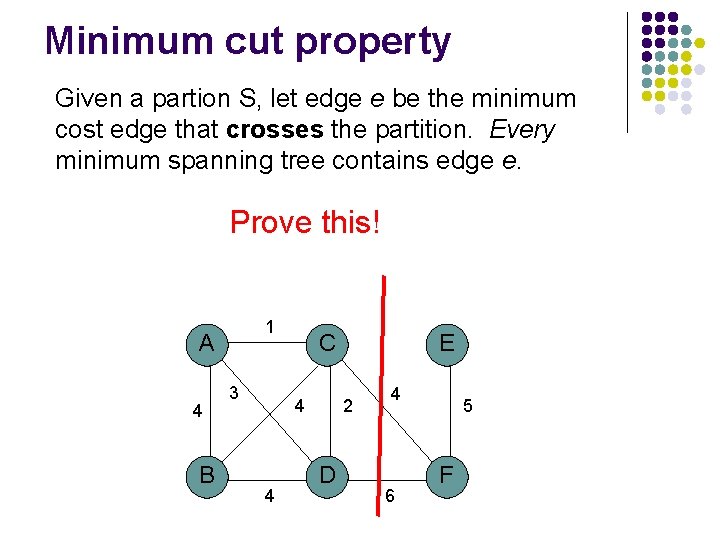
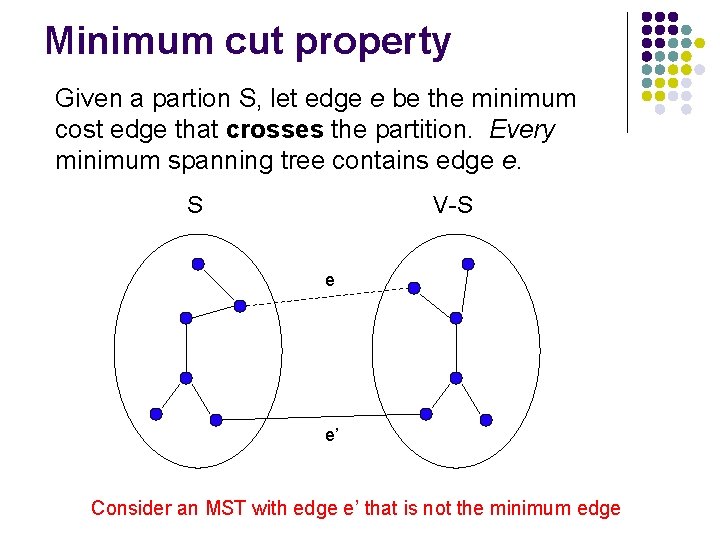
Minimum cut property Given a partion S, let edge e be the minimum cost edge that crosses the partition. Every minimum spanning tree contains edge e. Prove this! 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F

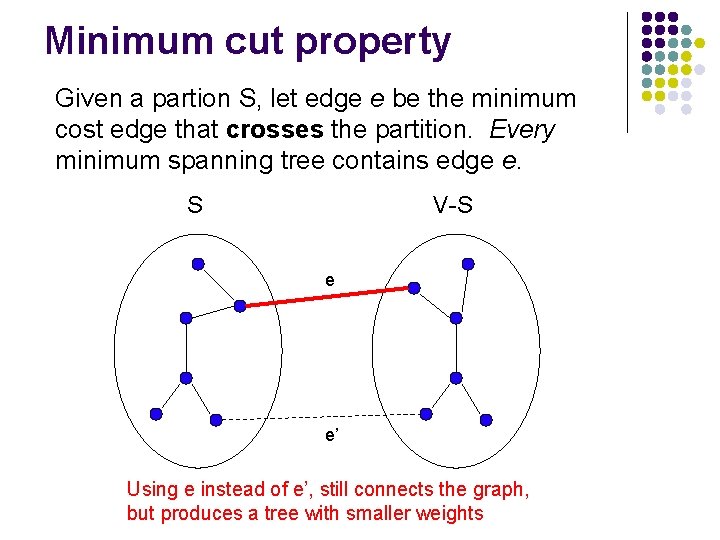
Minimum cut property Given a partion S, let edge e be the minimum cost edge that crosses the partition. Every minimum spanning tree contains edge e. S V-S e e’ Consider an MST with edge e’ that is not the minimum edge

Minimum cut property Given a partion S, let edge e be the minimum cost edge that crosses the partition. Every minimum spanning tree contains edge e. S V-S e e’ Using e instead of e’, still connects the graph, but produces a tree with smaller weights

Kruskal’s algorithm Given a partition S, let edge e be the minimum cost edge that crosses the partition. Every minimum spanning tree contains edge e.

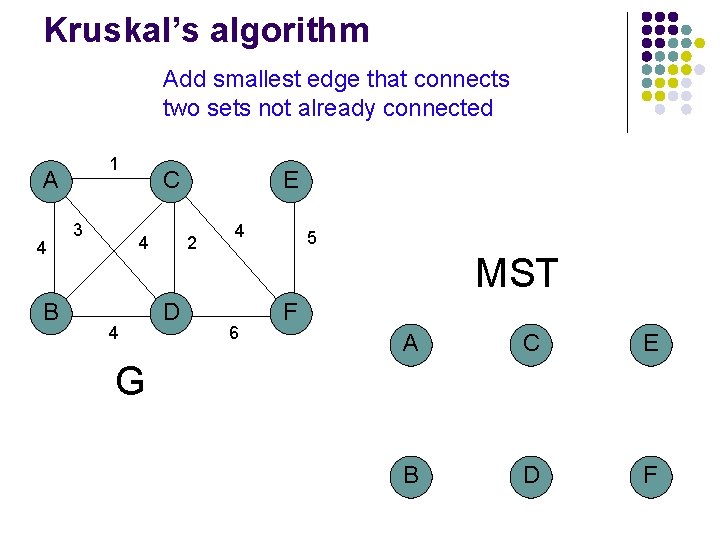
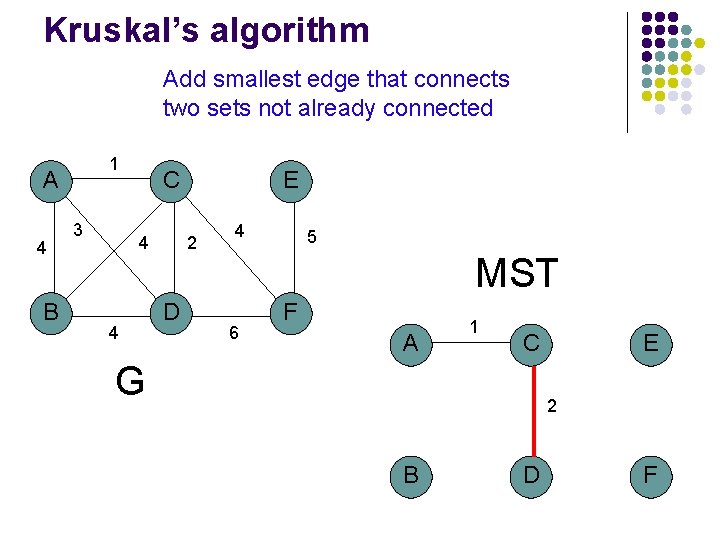
Kruskal’s algorithm Add smallest edge that connects two sets not already connected 1 A 4 B 3 C 4 4 E 2 D 4 5 MST 6 F A C E B D F G

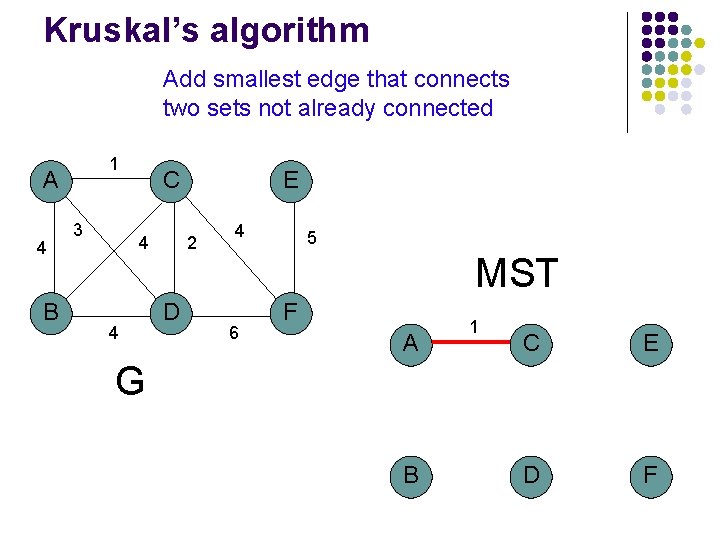
Kruskal’s algorithm Add smallest edge that connects two sets not already connected 1 A 4 B 3 C 4 4 E 2 D 4 5 MST 6 F A 1 C E D F G B

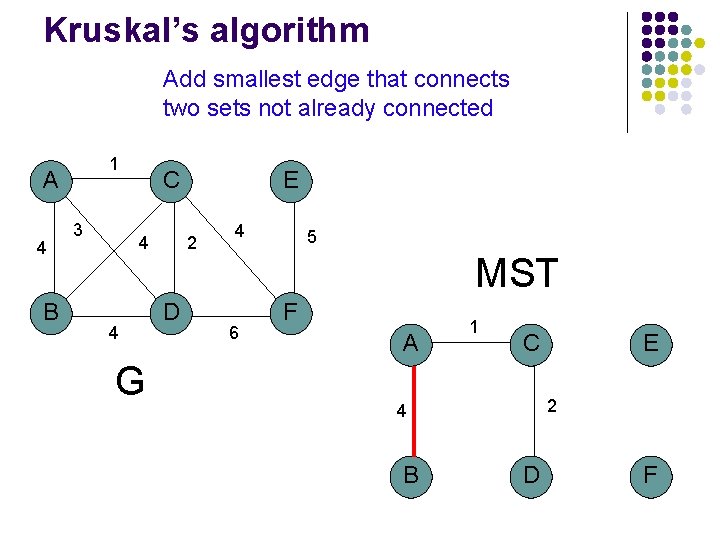
Kruskal’s algorithm Add smallest edge that connects two sets not already connected 1 A 4 B 3 C 4 4 E 2 D 4 5 MST 6 F A 1 C G E 2 B D F

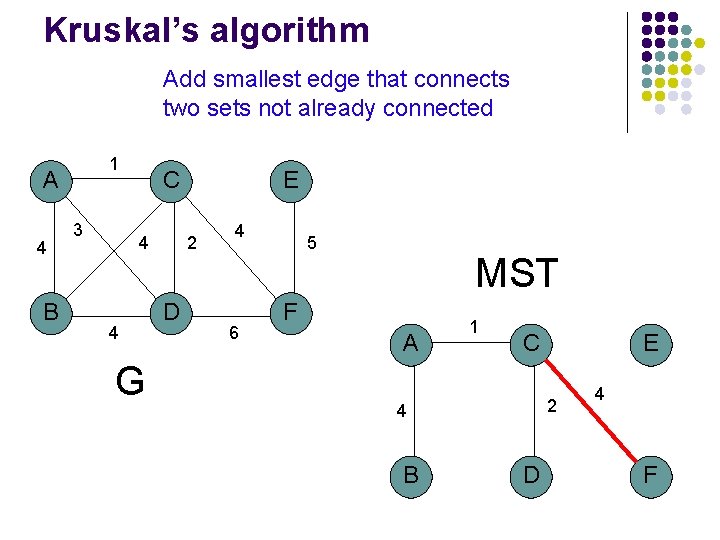
Kruskal’s algorithm Add smallest edge that connects two sets not already connected 1 A 4 B 3 C 4 4 G E 2 D 4 5 MST 6 F A 1 C 2 4 B E D F

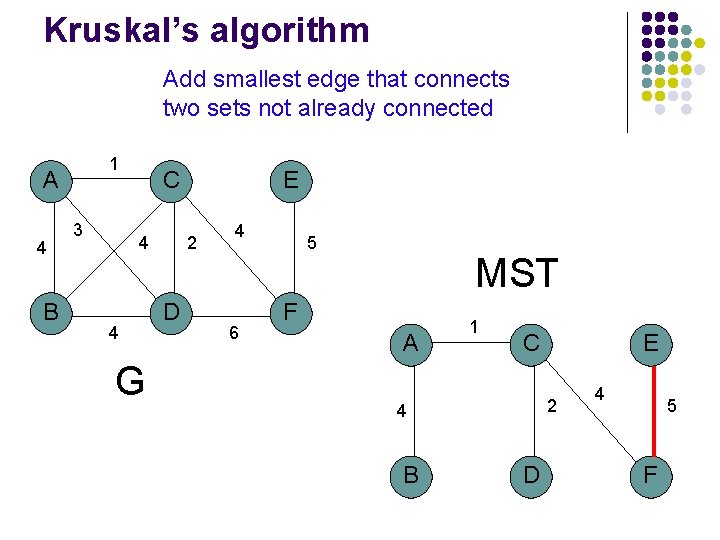
Kruskal’s algorithm Add smallest edge that connects two sets not already connected 1 A 4 B 3 C 4 4 G E 2 D 4 6 5 MST F A 1 C 2 4 B E D 4 F

Kruskal’s algorithm Add smallest edge that connects two sets not already connected 1 A 4 B 3 C 4 4 G E 2 D 4 6 5 MST F A 1 C 2 4 B E D 4 5 F

Correctness of Kruskal’s Never adds an edge that connects already connected vertices Always adds lowest cost edge to connect two sets. By min cut property, that edge must be part of the MST

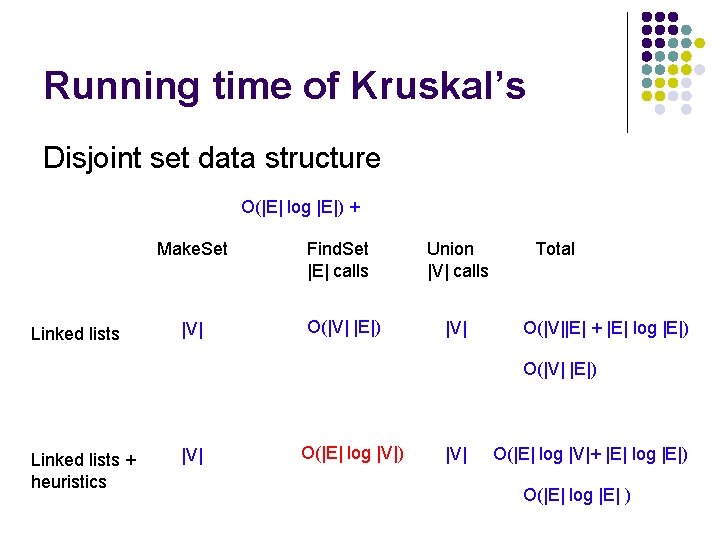
Running time of Kruskal’s

Running time of Kruskal’s |V| calls to Make. Set O(|E| log |E|) 2 |E| calls to Find. Set |V| calls to Union

Running time of Kruskal’s Disjoint set data structure O(|E| log |E|) + Make. Set Linked lists |V| Find. Set |E| calls O(|V| |E|) Union |V| calls |V| Total O(|V||E| + |E| log |E|) O(|V| |E|) Linked lists + heuristics |V| O(|E| log |V|) |V| O(|E| log |V|+ |E| log |E|) O(|E| log |E| )

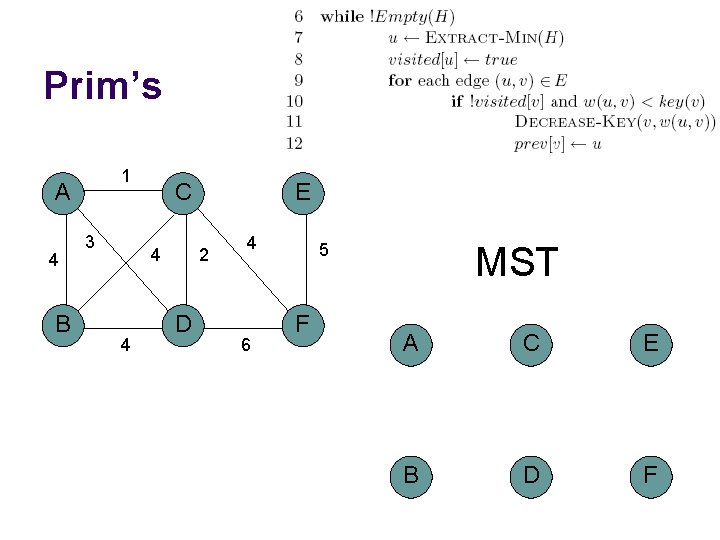
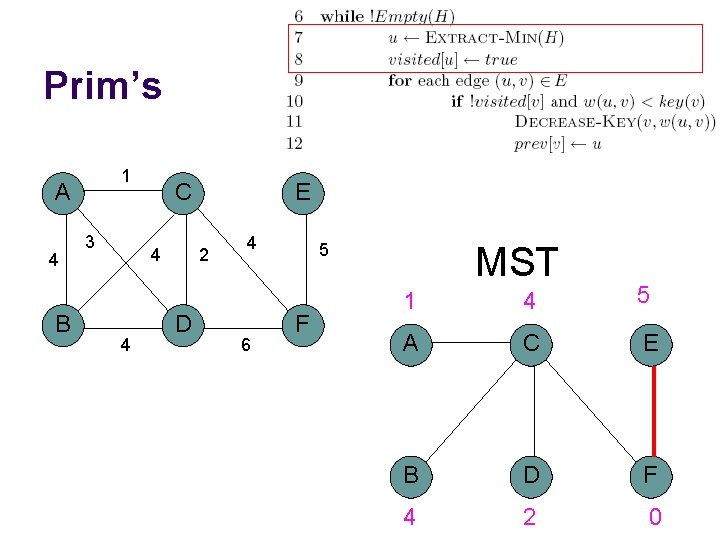
Prim’s algorithm

Prim’s algorithm

Prim’s algorithm

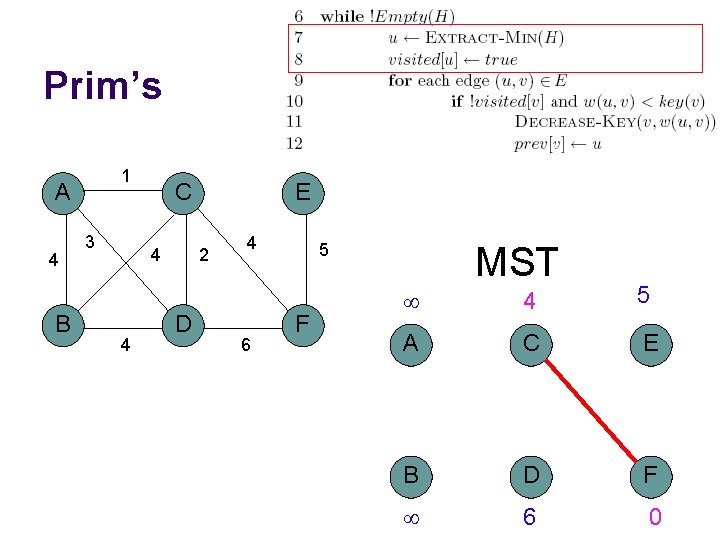
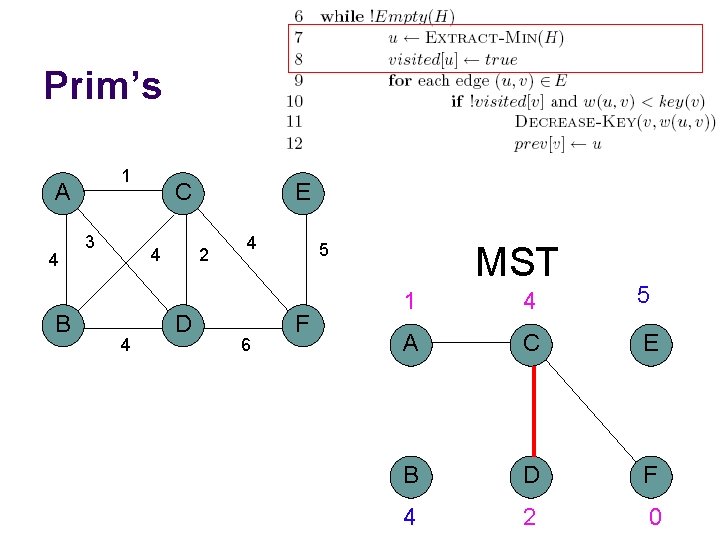
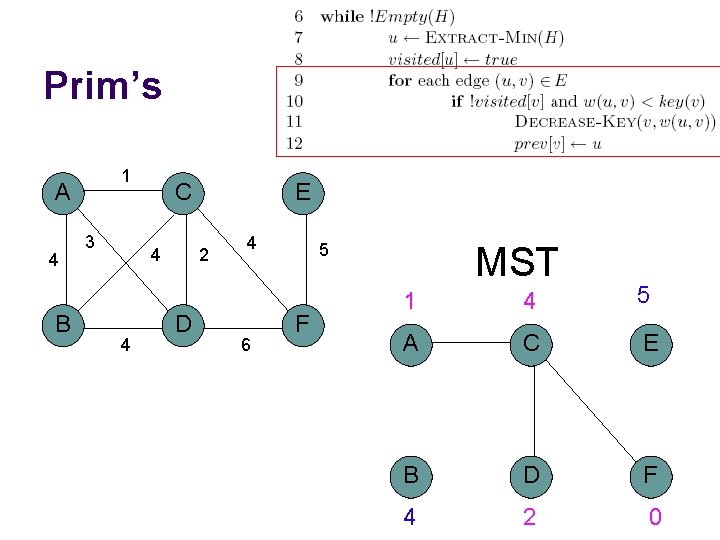
Prim’s algorithm Start at some root node and build out the MST by adding the lowest weighted edge at the frontier

Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST A C E B D F

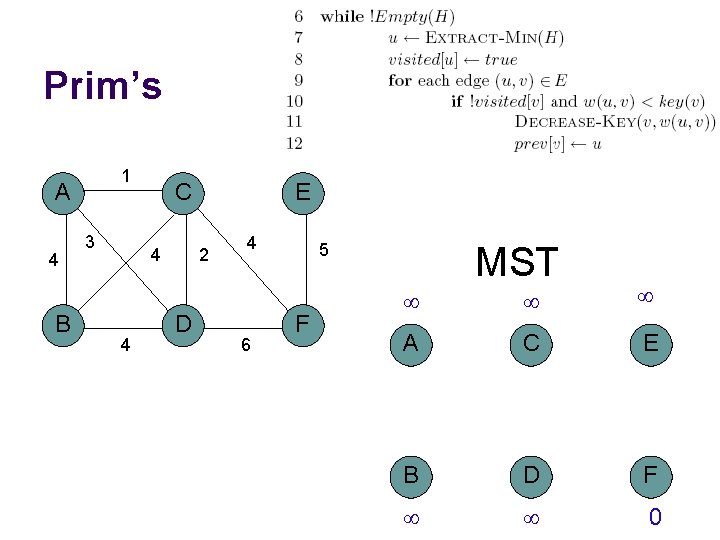
Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST A C E B D F 0

Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST 4 5 A C E B D F 6 0

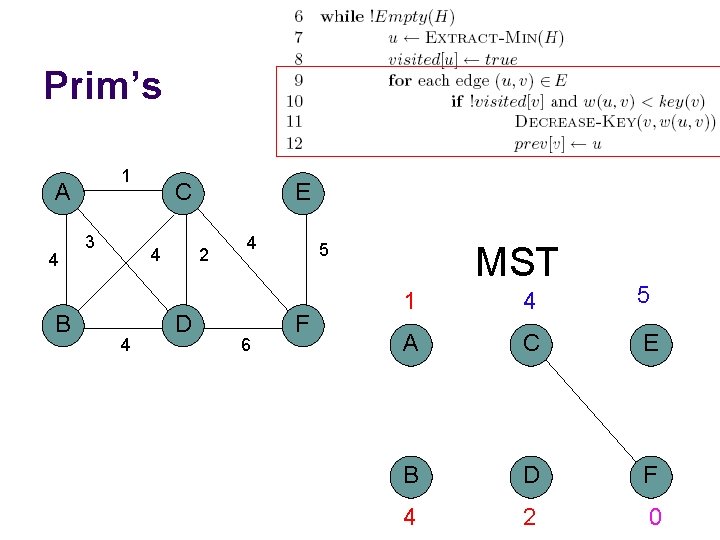
Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST 4 5 A C E B D F 6 0

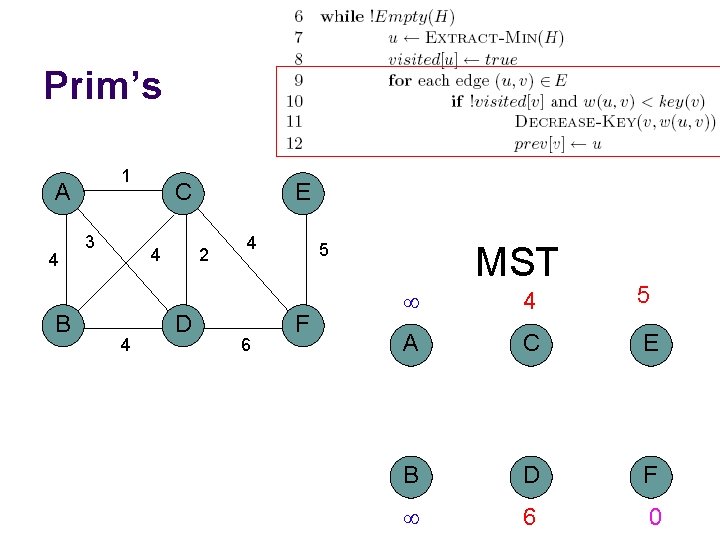
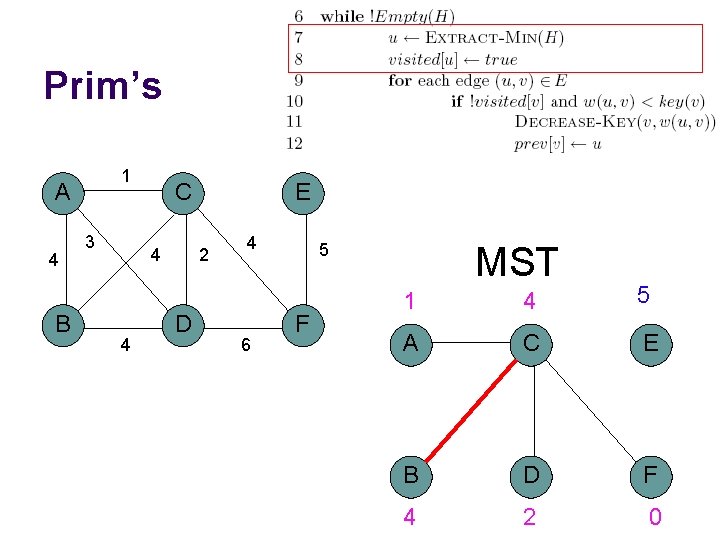
Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST 1 4 5 A C E B D F 4 2 0

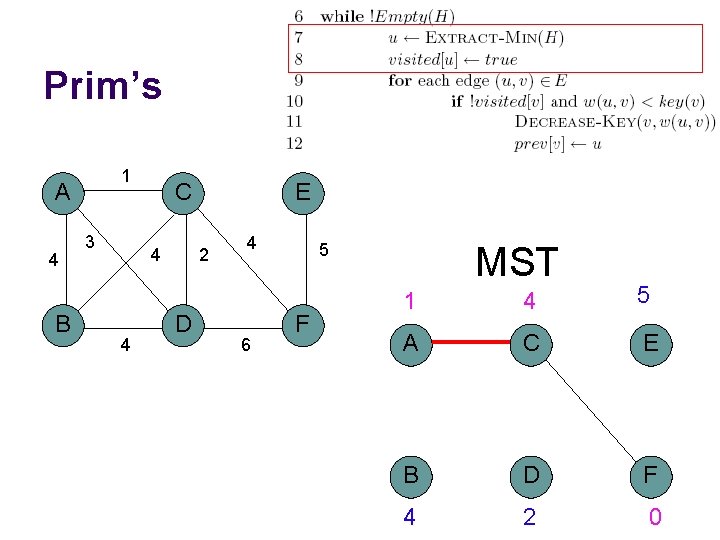
Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST 1 4 5 A C E B D F 4 2 0

Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST 1 4 5 A C E B D F 4 2 0

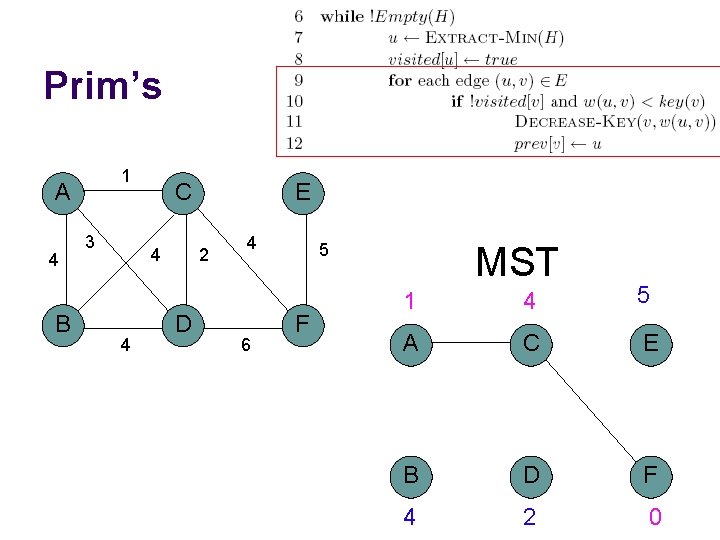
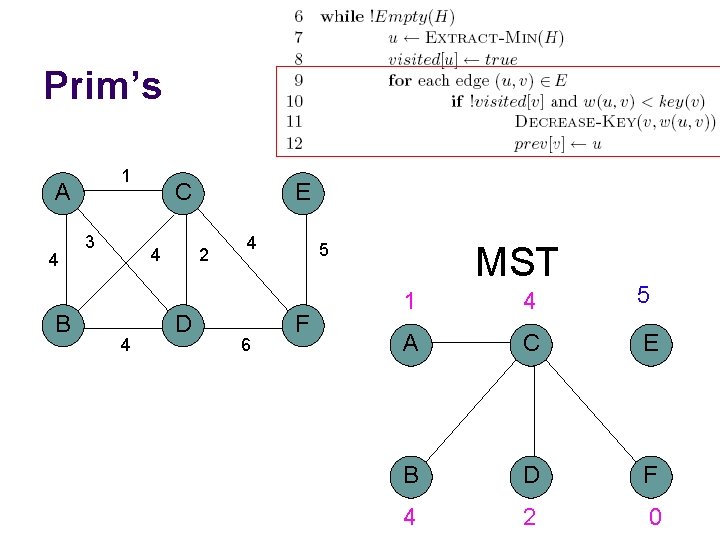
Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST 1 4 5 A C E B D F 4 2 0

Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST 1 4 5 A C E B D F 4 2 0

Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST 1 4 5 A C E B D F 4 2 0

Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST 1 4 5 A C E B D F 4 2 0

Prim’s 1 A 4 B 3 C 4 4 E 2 D 4 6 5 F MST 1 4 5 A C E B D F 4 2 0

Correctness of Prim’s? Can we use the min-cut property? l Given a partion S, let edge e be the minimum cost edge that crosses the partition. Every minimum spanning tree contains edge e. Let S be the set of vertices visited so far The only time we add a new edge is if it’s the lowest weight edge from S to V-S

Running time of Prim’s

Running time of Prim’s Θ(|V|) |V| calls to Extract-Min |E| calls to Decrease-Key

Running time of Prim’s Same as Dijksta’s algorithm 1 Make. Heap |V| Extract. Min |E| Decrease. Key Array O(|V|) O(|V|2) O(|E|) Bin heap O(|V|) O(|V| log |V|) O(|E| log |V|) Total O(|V|2) O((|V|+|E|) log |V|) O(|E| log |V|) Fib heap O(|V|) O(|V| log |V|) O(|E|) O(|V| log |V| + |E|) Kruskal’s: O(|E| log |E| )