Graphs shortest paths Minimum Spanning TreeMST 15 211

Graphs: shortest paths & Minimum Spanning Tree(MST) 15 -211 Fundamental Data Structures and Algorithms Ananda Guna April 8, 2003 1

Announcements § Homework #5 is due Tuesday April 15 th. § Quiz #3 feedback is enabled. § Final Exam is Tuesday May 8 th at 8 AM 2

Recap 3

Dijkstra’s algorithm § S = {1} § for i = 2 to n do D[i] = C[1, i] if there is an edge from 1 to i, infinity otherwise § for i = 1 to n-1 { choose a vertex w in V-S such that D[w] is min add w to S (where S is the set of visited nodes) for each vertex v in V-S do D[v] = min(D[v], D[w]+c[w, v]) } Where |V| = n 4

Features of Dijkstra’s Algorithm • A greedy algorithm • “Visits” every vertex only once, when it becomes the vertex with minimal distance amongst those still in the priority queue • Distances may be revised multiple times: current values represent ‘best guess’ based on our observations so far • Once a vertex is visited we are guaranteed to have found the shortest path to that vertex…. why? 5

Correctness (via contradiction) • Prove D(u) represent the shortest path to u (visited node) • Assume u is the first vertex visited such that D(u) is not a shortest path (thus the true shortest path to u must pass through some unvisited vertex) • Let x represent the first unvisited vertex on the true unvisited shortest path to u visited x s u • D(x) must represent a shortest path to x, and D(x) Dshortest(u). • However, Dijkstra’s always visits the vertex with the smallest distance next, so we can’t possibly visit u before we visit x 6

Quiz break § Would it be better to use an adjacency list or an adjacency matrix for Dijkstra’s algorithm? § What is the running time of Dijkstra’s algorithm, in terms of |V| and |E| in each case? 7

Complexity of Dijkstra § Adjacency matrix version Dijkstra finds shortest path from one vertex to all others in O(|V|2) time § If |E| is small compared to |V|2, use a priority queue to organize the vertices in V -S, where V is the set of all vertices and S is the set that has already been explored Ø So total of |E| updates each at a cost of O(log |V|) Ø So total time is O(|E| log|V|) 8

Negative Weighted Single-Source Shortest Path Algorithm (Bellman-Ford Algorithm) 9

The Bellman-Ford algorithm (see Weiss, Section 14. 4) Returns a boolean: • TRUE if and only if there is no negative-weight cycle reachable from the source: a simple cycle <v 0, v 1, …, vk>, where v 0=vk and • FALSE otherwise If it returns TRUE, it also produces the shortest paths 10

Example § For each edge (u, v), let's denote its length by C(u, v)) § Let d[i][v] = distance from start to v using the shortest path out of all those that use i or fewer edges, or infinity if you can't get there with <= i edges. 11

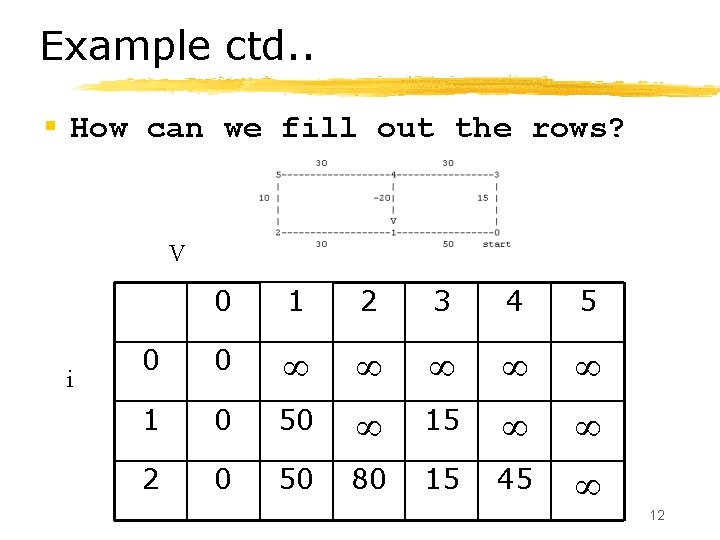
Example ctd. . § How can we fill out the rows? V i 0 1 2 3 4 5 0 0 1 0 50 15 2 0 50 80 15 45 12

Example ctd. . § Can we get ith row from i-1 th row? § for v != start, d[v][i] = MIN d[x][i-1] + len(x, v) x->v § We know minimum path to come to x using < i nodes. So for all x that can reach v, find the minimum such sum (in blue) among all x § Assume d[start][i] = 0 for all i 13

Completing the table d[v][i] = MIN d[x][i-1] + len(x, v) x->v 1 2 3 4 5 0 0 0 1 0 50 15 2 0 50 80 15 45 3 4 5 0 0 0 25 25 25 80 55 55 15 15 15 45 45 45 75 75 65 14

Key features • If the graph contains no negative-weight cycles reachable from the source vertex, after |V| - 1 iterations all distance estimates represent shortest paths…why? 15

Correctness Case 1: Graph G=(V, E) doesn’t contain any negativeweight cycles reachable from the source vertex s Consider a shortest path p = < v 0, v 1, . . . , vk>, which must have k |V| - 1 edges By induction: • D(s) = 0 after initialization • Assume D(vi-1) is a shortest path after iteration (i-1) • Since edge (vi-1, vi) is updated on the ith pass, D(vi) must then reflect the shortest path to vi. • Since we perform |V| - 1 iterations, D(vi) for all reachable vertices vi must now represent shortest paths The algorithm will return true because on the |V|th iteration, no distances will change 16

Correctness Case 2: Graph G=(V, E) contains a negative-weight cycle < v 0, v 1, . . . , vk> reachable from the source vertex s Proof by contradiction: Assume the algorithm returns TRUE Thus, D(vi-1) + weight(vi-1, vi) D(vi) for i = 1, …, k Summing the inequalities for the cycle: leads to a contradiction since the first sums on each side are equal (each vertex appears exactly once) and the sum of weights must be less than 0. 17

Performance Initialization: O(|V|) Path update and cycle check: |V| calls checking |E| edges, O(|VE|) Overall cost: O(|VE|) 18

The All Pairs Shortest Path Algorithm (Floyd’s Algorithm) 19

Finding all pairs shortest paths § Assume G=(V, E) is a graph such that c[v, w] 0, where C is the matrix of edge costs. § Find for each pair (v, w), the shortest path from v to w. That is, find the matrix of shortest paths § Certainly this is a generalization of Dijkstra’s. § Note: For later discussions assume |V| = n and |E| = m 20

Floyd’s Algorithm § A[i][j] = C(i, j) if there is an edge (i, j) § A[i][j] = infinity(inf) if there is no edge (i, j) Graph “adjacency” matrix A is the shortest path matrix that uses 1 or fewer edges 21

Floyd ctd. . § To find shortest paths that uses 2 or fewer edges find A 2, where multiplication defined as min of sums instead sum of products § That is (A 2)ij = min{ Aik + Akj | k =1. . n} § This operation is O(n 3) § Using A 2 you can find A 4 and then A 8 and so on § Therefore to find An we need log n operations § Therefore this algorithm is O(log n* n 3) § We will consider another algorithm next 22

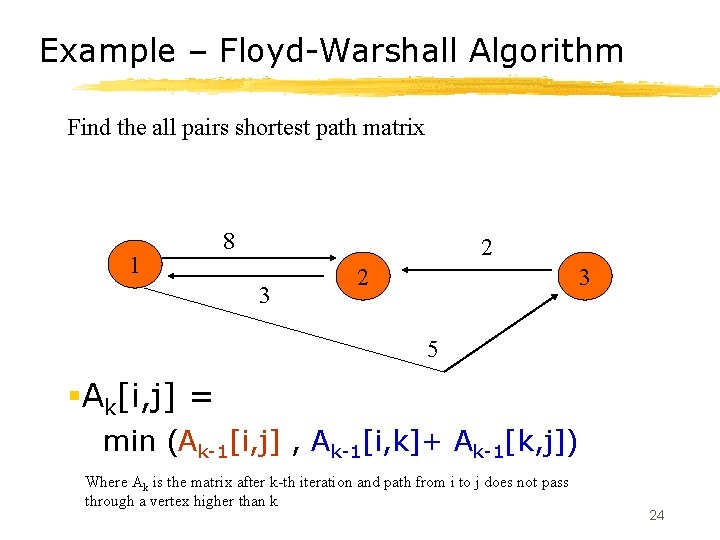
Floyd-Warshall Algorithm § This algorithm uses nxn matrix A to compute the lengths of the shortest paths using a dynamic programming technique. § Let A[i, j] = c[i, j] for all i, j & i j § If (i, j) is not an edge, set A[i, j]=infinity and A[i, i]=0 § Ak[i, j] = min (Ak-1[i, j] , Ak-1[i, k]+ Ak-1[k, j]) Where Ak is the matrix after k-th iteration and path from i to j does not pass through a vertex higher than k 23

Example – Floyd-Warshall Algorithm Find the all pairs shortest path matrix 1 8 2 3 5 §Ak[i, j] = min (Ak-1[i, j] , Ak-1[i, k]+ Ak-1[k, j]) Where Ak is the matrix after k-th iteration and path from i to j does not pass through a vertex higher than k 24

Floyd-Warshall Implementation § initialize A[i, j] = C[i, j] § initialize all A[i, i] = 0 § for k from 1 to n for i from 1 to n for j from 1 to n if (A[i, j] > A[i, k]+A[k, j]) A[i, j] = A[i, k]+A[k, j]; § The complexity of this algorithm is O(n 3) 25

Questions § Question: What is the asymptotic run time of Dijkstra (adjacency matrix version)? ØO(n 2) § Question: What is the asymptotic running time of Floyd-Warshall? 26

Minimum Spanning Trees (some material adapted from slides by Peter Lee) 27

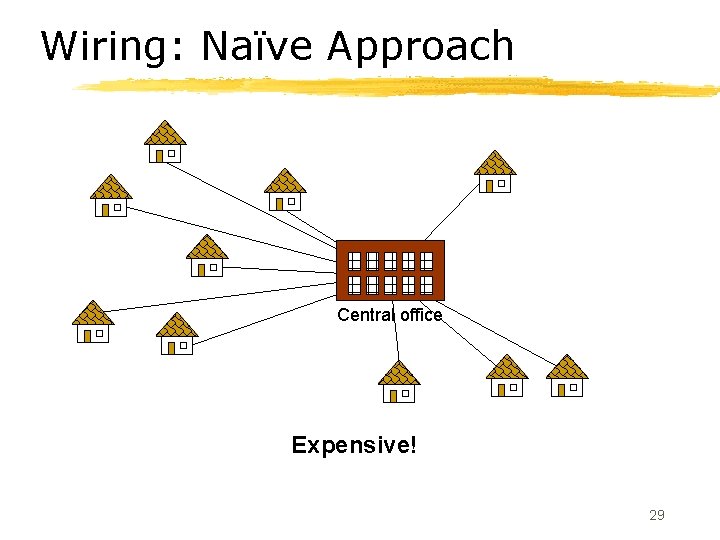
Problem: Laying Telephone Wire Central office 28

Wiring: Naïve Approach Central office Expensive! 29

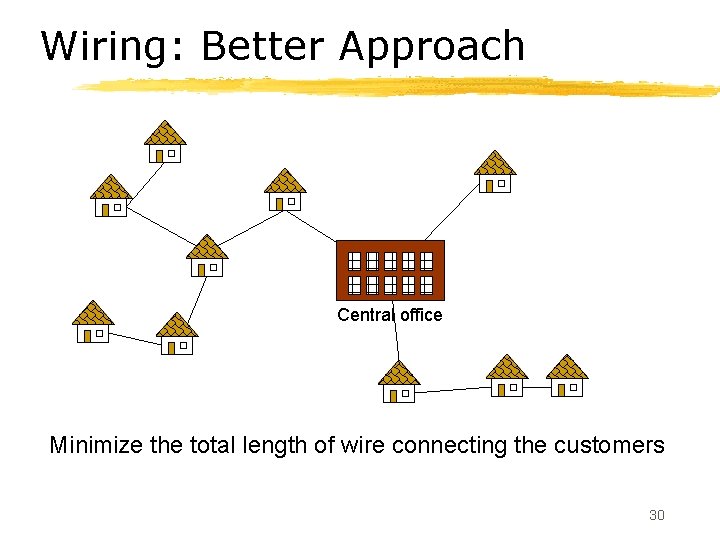
Wiring: Better Approach Central office Minimize the total length of wire connecting the customers 30

Minimum Spanning Tree (MST) (see Weiss, Section 24. 2. 2) A minimum spanning tree is a subgraph of an undirected weighted graph G, such that § it is a tree (i. e. , it is acyclic) § it covers all the vertices V Ø contains |V| - 1 edges § the total cost associated with tree edges is the minimum among all possible spanning trees § not necessarily unique 31

Applications of MST § Any time you want to visit all vertices in a graph at minimum cost (e. g. , wire routing on printed circuit boards, sewer pipe layout, road planning…) § Internet content distribution Ø $$$, also a hot research topic Ø Idea: publisher produces web pages, content distribution network replicates web pages to many locations so consumers can access at higher speed Ø MST may not be good enough! § content distribution on minimum cost tree may take a long time! 32

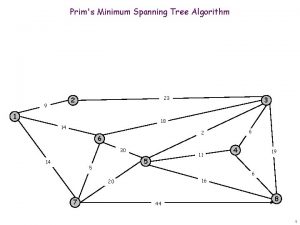
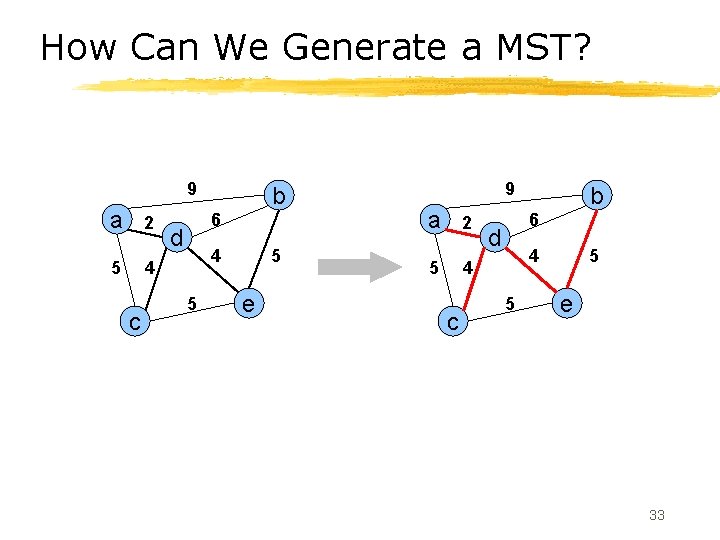
How Can We Generate a MST? 9 a 2 5 4 c b 6 d 4 5 5 e 33

Prim’s Algorithm § Let V ={1, 2, . . , n} and U be the set of vertices that makes the MST and T be the MST § Initially : U = {1} and T = § while (U V) let (u, v) be the lowest cost edge such that u U and v V-U T = T {(u, v)} U = U {v} 34

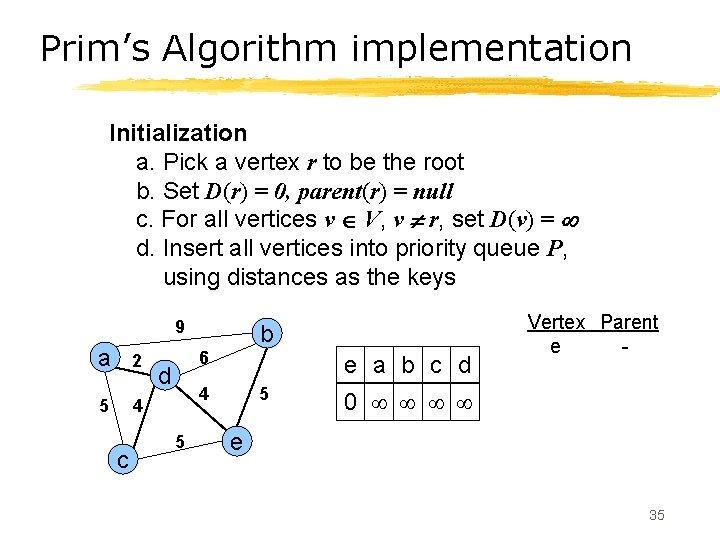
Prim’s Algorithm implementation Initialization a. Pick a vertex r to be the root b. Set D(r) = 0, parent(r) = null c. For all vertices v V, v r, set D(v) = d. Insert all vertices into priority queue P, using distances as the keys 9 a 2 5 4 c b 6 d e a b c d 4 5 5 Vertex Parent e - 0 e 35

Prim’s Algorithm While P is not empty: 1. Select the next vertex u to add to the tree u = P. delete. Min() 2. Update the weight of each vertex w adjacent to u which is not in the tree (i. e. , w P) If weight(u, w) < D(w), a. parent(w) = u b. D(w) = weight(u, w) c. Update the priority queue to reflect new distance for w 36

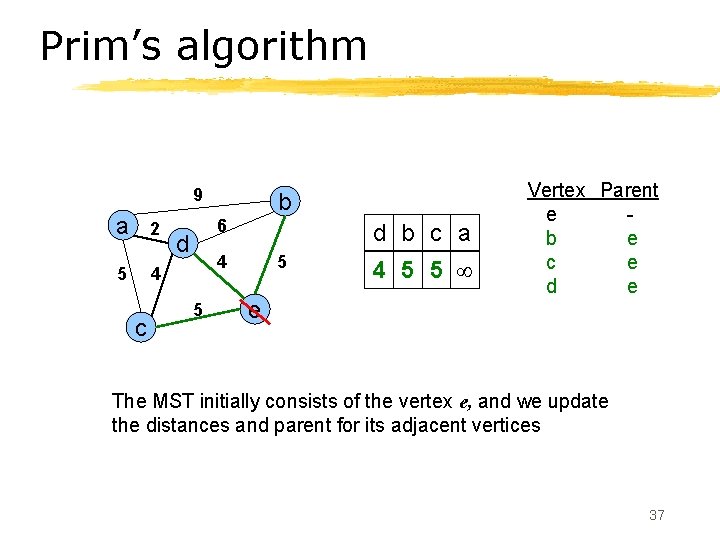
Prim’s algorithm 9 a 2 5 4 c b 6 d d b c a 4 5 5 e 4 5 5 Vertex Parent e b e c e d e The MST initially consists of the vertex e, and we update the distances and parent for its adjacent vertices 37

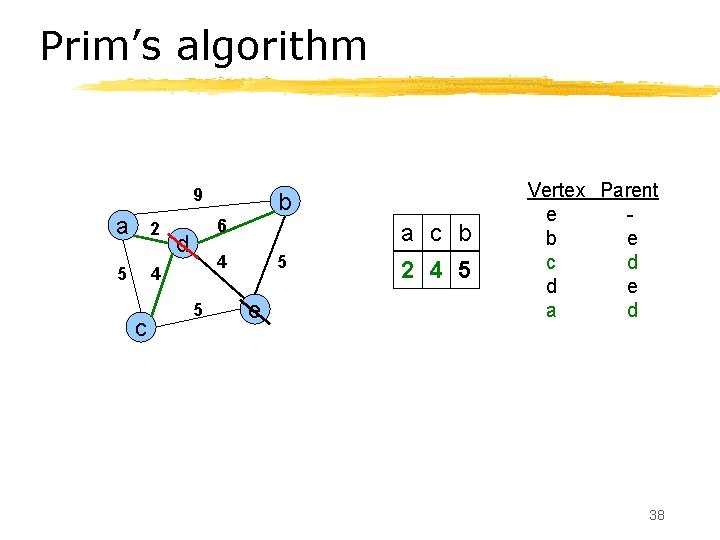
Prim’s algorithm 9 a 2 5 4 c b 6 d a c b 4 5 5 e 2 4 5 Vertex Parent e b e c d d e a d 38

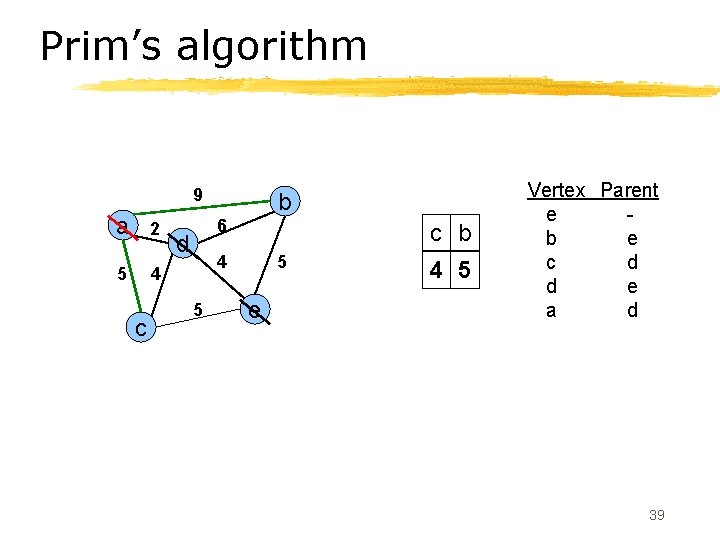
Prim’s algorithm 9 a 2 5 4 c b 6 d c b 4 5 5 e 4 5 Vertex Parent e b e c d d e a d 39

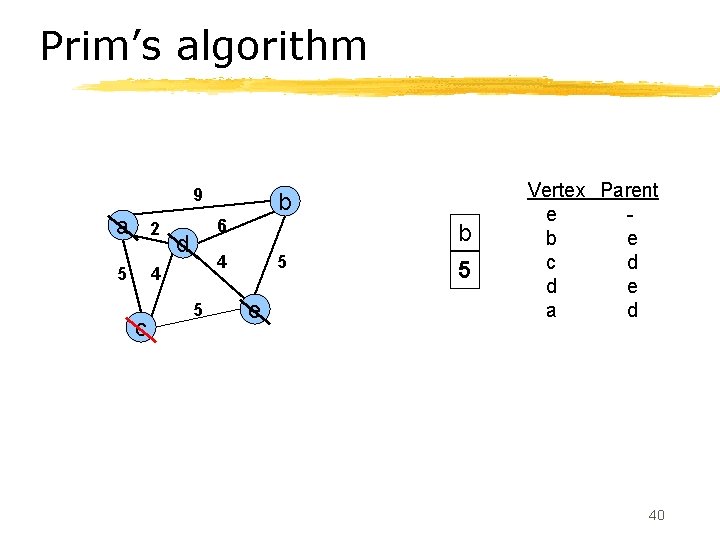
Prim’s algorithm 9 a 2 5 4 c b 6 d b 4 5 5 e 5 Vertex Parent e b e c d d e a d 40

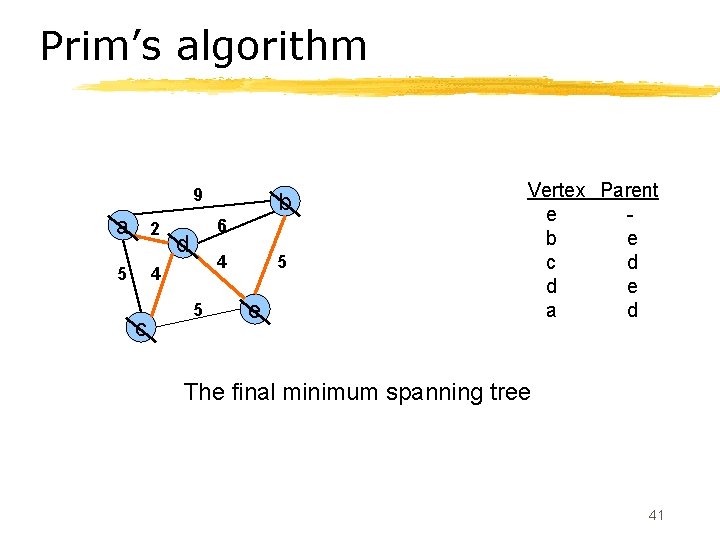
Prim’s algorithm 9 a 2 5 4 c b 6 d 4 5 5 e Vertex Parent e b e c d d e a d The final minimum spanning tree 41

Prim’s Algorithm Invariant § At each step, we add the edge (u, v) s. t. the weight of (u, v) is minimum among all edges where u is in the tree and v is not in the tree § Each step maintains a minimum spanning tree of the vertices that have been included thus far § When all vertices have been included, we have a MST for the graph! 42

Running time of Prim’s algorithm Initialization of priority queue (array): O(|V|) Update loop: |V| calls • Choosing vertex with minimum cost edge: O(|V|) • Updating distance values of unconnected vertices: each edge is considered only once during entire execution, for a total of O(|E|) updates O(|E| + |V| 2) Overall cost: 43

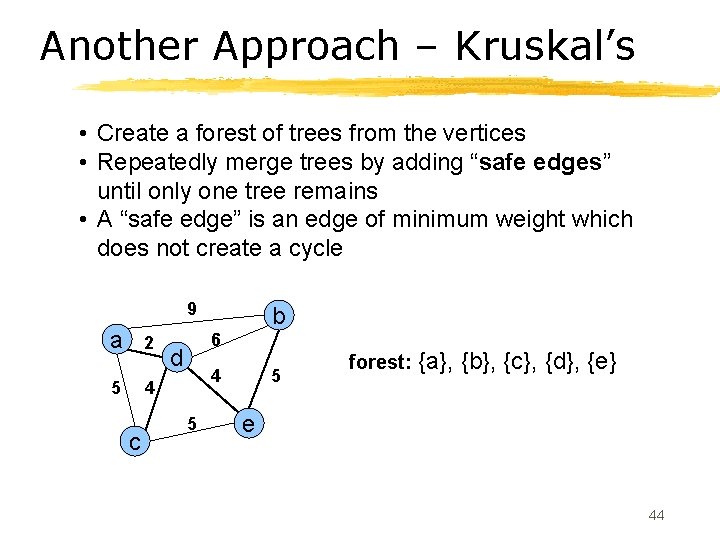
Another Approach – Kruskal’s • Create a forest of trees from the vertices • Repeatedly merge trees by adding “safe edges” until only one tree remains • A “safe edge” is an edge of minimum weight which does not create a cycle 9 a 2 5 6 d 4 4 c b 5 5 forest: {a}, {b}, {c}, {d}, {e} e 44

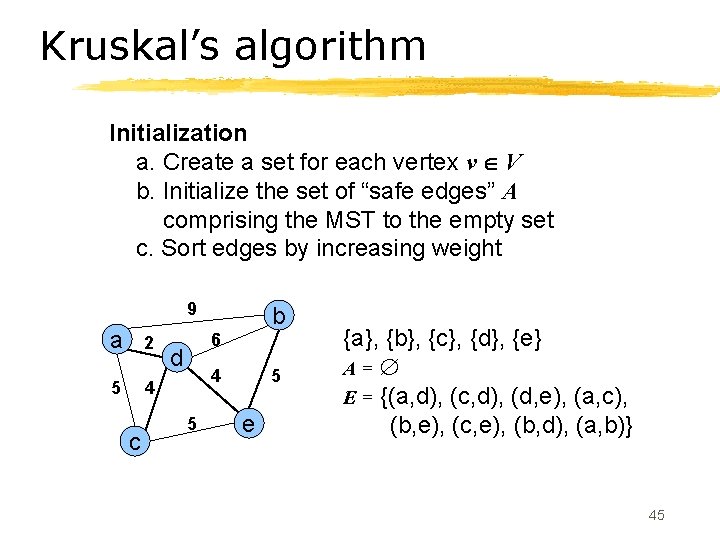
Kruskal’s algorithm Initialization a. Create a set for each vertex v V b. Initialize the set of “safe edges” A comprising the MST to the empty set c. Sort edges by increasing weight 9 a 2 5 4 c b 6 d 4 5 5 e {a}, {b}, {c}, {d}, {e} A= E = {(a, d), (c, d), (d, e), (a, c), (b, e), (c, e), (b, d), (a, b)} 45

Kruskal’s algorithm For each edge (u, v) E in increasing order while more than one set remains: If u and v, belong to different sets a. A = A {(u, v)} b. merge the sets containing u and v Return A § Use Union-Find algorithm to efficiently determine if u and v belong to different sets 46

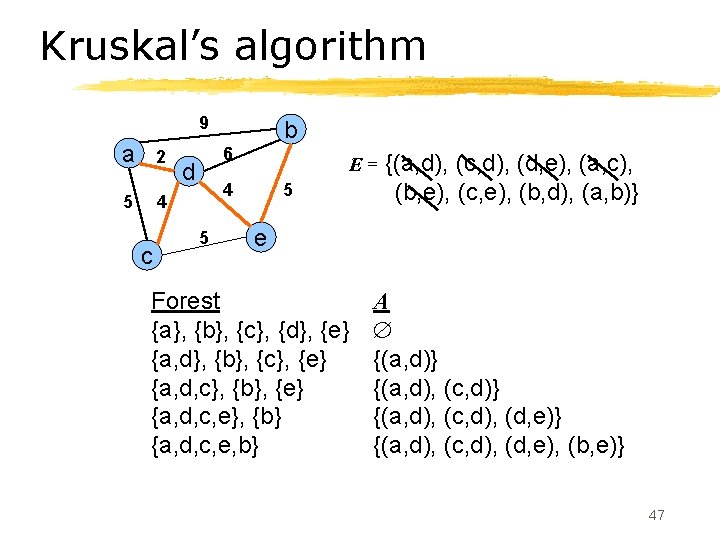
Kruskal’s algorithm 9 a 2 5 4 c b 6 d E= 4 5 5 {(a, d), (c, d), (d, e), (a, c), (b, e), (c, e), (b, d), (a, b)} e Forest {a}, {b}, {c}, {d}, {e} {a, d}, {b}, {c}, {e} {a, d, c}, {b}, {e} {a, d, c, e}, {b} {a, d, c, e, b} A {(a, d)} {(a, d), (c, d), (d, e)} {(a, d), (c, d), (d, e), (b, e)} 47

Kruskal’s Algorithm Invariant § After each iteration, every tree in the forest is a MST of the vertices it connects § Algorithm terminates when all vertices are connected into one tree 48

Greedy Approach § Like Dijkstra’s algorithm, both Prim’s and Kruskal’s algorithms are greedy algorithms § The greedy approach works for the MST problem; however, it does not work for many other problems! 49

Thursday § P vs NP § Models of Hard Problems § Work on Homework 5 50