CS 2133 Algorithms Minimum Spanning Tree Shortest Paths

CS 2133: Algorithms Minimum Spanning Tree Shortest Paths

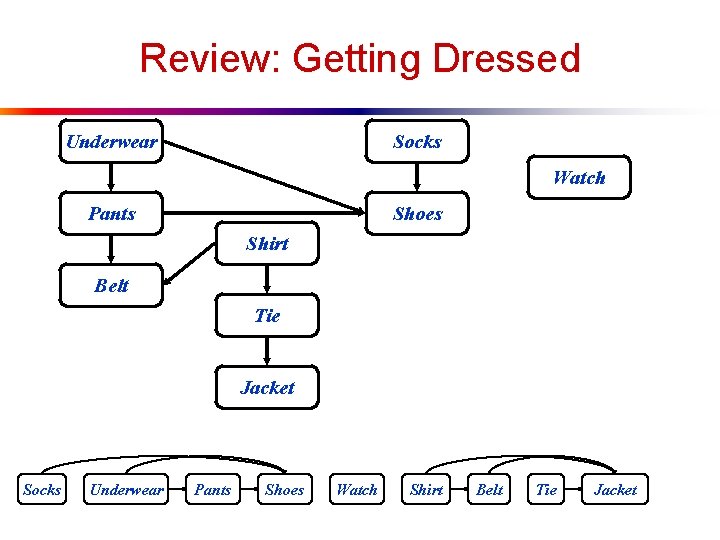
Review: Getting Dressed Underwear Socks Watch Pants Shoes Shirt Belt Tie Jacket Socks Underwear Pants Shoes Watch Shirt Belt Tie Jacket

Review: Topological Sort Algorithm Topological-Sort() { Run DFS When a vertex is finished, output it Vertices are output in reverse topological order } l Time: O(V+E)

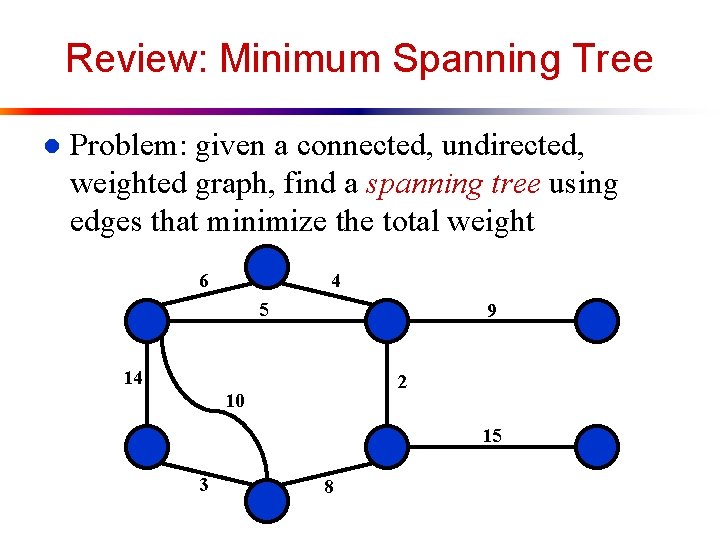
Review: Minimum Spanning Tree l Problem: given a connected, undirected, weighted graph, find a spanning tree using edges that minimize the total weight 6 4 5 9 14 2 10 15 3 8

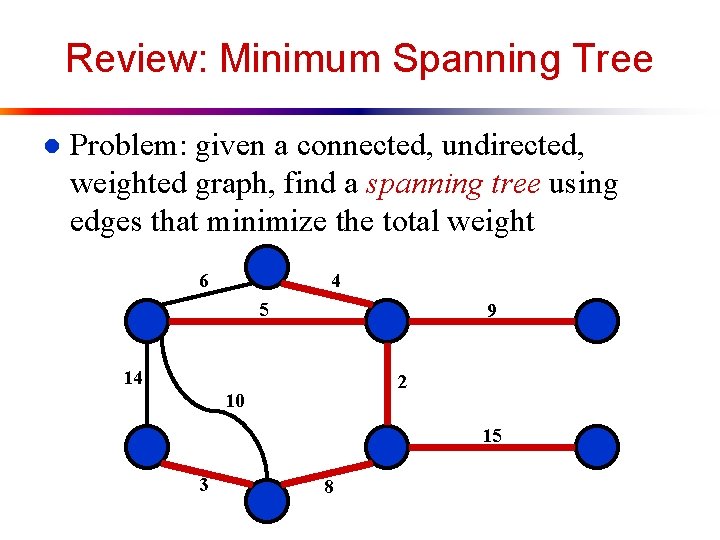
Review: Minimum Spanning Tree l Problem: given a connected, undirected, weighted graph, find a spanning tree using edges that minimize the total weight 6 4 5 9 14 2 10 15 3 8

Review: Minimum Spanning Tree l l MSTs satisfy the optimal substructure property: an optimal tree is composed of optimal subtrees If T is MST of G, and A T is a subtree of T, and (u, v) is the min-weight edge connecting A to V-A, then (u, v) T

Prim’s Algorithm MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; p[r] = NULL; 3 8 while (Q not empty) Run on example graph u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; p[r] = NULL; 3 8 while (Q not empty) Run on example graph u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 r p[r] = NULL; 3 8 while (Q not empty) Pick a start vertex r u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 u p[r] = NULL; 3 8 while (Q not empty) u = Extract. Min(Q); Red vertices have been removed from Q for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 u p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); Red arrows indicate parent pointers for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 14 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 u p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 14 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 14 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15 15

Prim’s Algorithm u MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 10 2 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 15

Prim’s Algorithm u MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 10 2 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm u 4 MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 10 2 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm u 4 MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 5 2 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm u 4 MST-Prim(G, w, r) 6 4 Q = V[G]; 5 5 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm u 4 MST-Prim(G, w, r) 6 4 Q = V[G]; 5 5 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm 4 MST-Prim(G, w, r) 6 4 Q = V[G]; 5 5 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); u 9 15

Prim’s Algorithm 4 MST-Prim(G, w, r) 6 4 Q = V[G]; 5 5 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 9 u 15 15

Review: Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; for each u Q key[u] = ; key[r] = 0; What is the hidden cost p[r] = NULL; while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); in this code?

Review: Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; for each u Q key[u] = ; key[r] = 0; p[r] = NULL; while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; Decrease. Key(v, w(u, v));

Review: Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; for each u Q key[u] = ; How often is Extract. Min() called? key[r] = 0; How often is Decrease. Key() called? p[r] = NULL; while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; Decrease. Key(v, w(u, v));

Review: Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; What will be the running for each u Q A: Depends on queue key[u] = ; binary heap: O(E lg V) key[r] = 0; p[r] = NULL; while (Q not empty) u = Extract. Min(Q); // log V for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); // decrease // key=O(log V) time?

Single-Source Shortest Path l Problem: given a weighted directed graph G, find the minimum-weight path from a given source vertex s to another vertex v n n n “Shortest-path” = minimum weight Weight of path is sum of edges E. g. , a road map: what is the shortest path from Chapel Hill to Charlottesville?

Shortest Path Properties l Again, we have optimal substructure: the shortest path consists of shortest subpaths: n Proof: suppose some subpath is not a shortest path u There must then exist a shorter subpath u Could substitute the shorter subpath for a shorter path u But then overall path is not shortest path. Contradiction

Shortest Path Properties Define (u, v) to be the weight of the shortest path from u to v l Shortest paths satisfy the triangle inequality: (u, v) (u, x) + (x, v) l “Proof”: x l u v This path is no longer than any other path

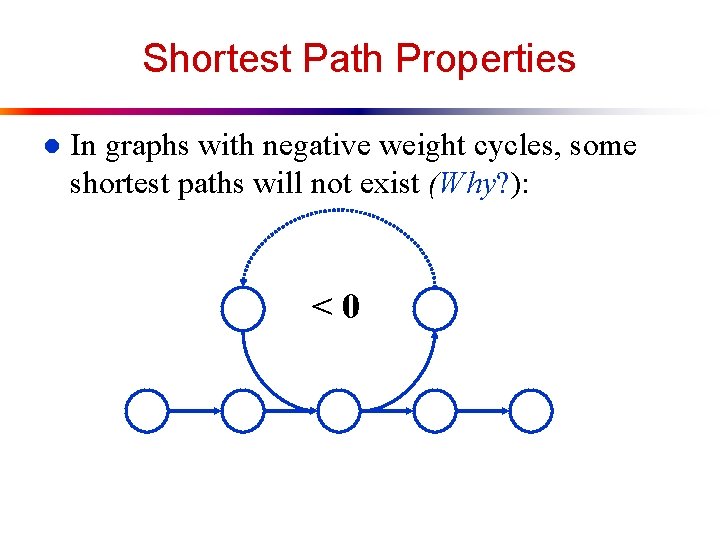
Shortest Path Properties l In graphs with negative weight cycles, some shortest paths will not exist (Why? ): <0

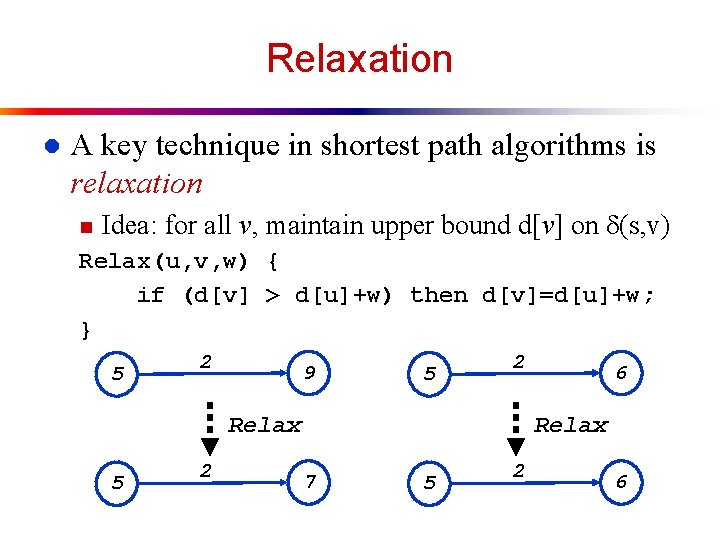
Relaxation l A key technique in shortest path algorithms is relaxation n Idea: for all v, maintain upper bound d[v] on (s, v) Relax(u, v, w) { if (d[v] > d[u]+w) then d[v]=d[u]+w; } 5 2 9 5 2 Relax 5 2 6 Relax 7 5 2 6

Dijkstra’s Algorithm Here we assume no negative edge weights l Similar to breadth-first search l n l Grow a tree gradually, advancing from vertices taken from a queue Also similar to Prim’s algorithm for MST n Use a priority queue keyed on d[v]

Dijkstra’s Algorithm Dijkstra(G) B 2 10 for each v V 4 3 d[v] = ; A D d[s] = 0; S = ; Q = V; 5 1 C while (Q ) u = Extract. Min(Q); Ex: run the algorithm S = S {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) d[v] = d[u]+w(u, v); Relaxation Note: this Step is really a call to Q->Decrease. Key()

Dijkstra’s Algorithm Dijkstra(G) How many times is for each v V Extract. Min() called? d[v] = ; d[s] = 0; S = ; Q = V; while (Q ) How many times is u = Extract. Min(Q); Decrease. Key() called? S = S {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) d[v] = d[u]+w(u, v); What will be the total running time?

Dijkstra’s Algorithm Dijkstra(G) How many times is for each v V Extract. Min() called? d[v] = ; d[s] = 0; S = ; Q = V; while (Q ) How many times is u = Extract. Min(Q); Decrase. Key() called? S = S {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) d[v] = d[u]+w(u, v); A: O(E lg V) using binary heap for Q Can acheive O(V lg V + E) with Fibonacci heaps

Dijkstra’s Algorithm Dijkstra(G) for each v V d[v] = ; d[s] = 0; S = ; Q = V; while (Q ) u = Extract. Min(Q); S = S {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) d[v] = d[u]+w(u, v); Correctness: we must show that when u is removed from Q, it has already converged

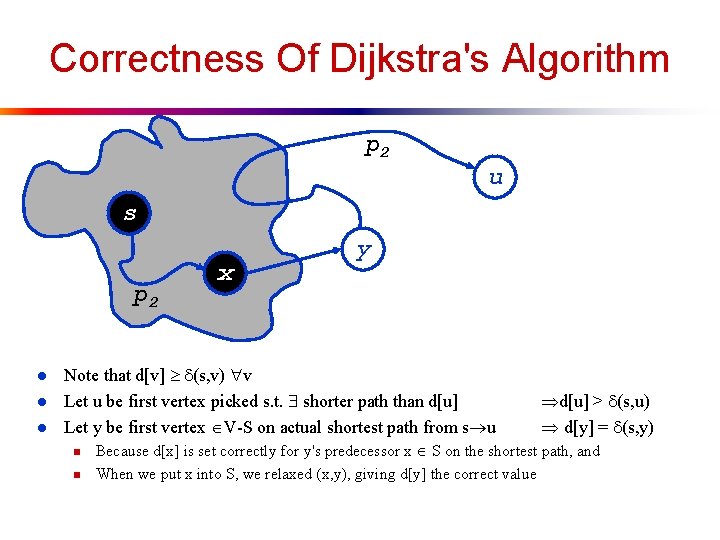
Correctness Of Dijkstra's Algorithm p 2 u s p 2 l l l x y Note that d[v] (s, v) v Let u be first vertex picked s. t. shorter path than d[u] Let y be first vertex V-S on actual shortest path from s u n n d[u] > (s, u) d[y] = (s, y) Because d[x] is set correctly for y's predecessor x S on the shortest path, and When we put x into S, we relaxed (x, y), giving d[y] the correct value

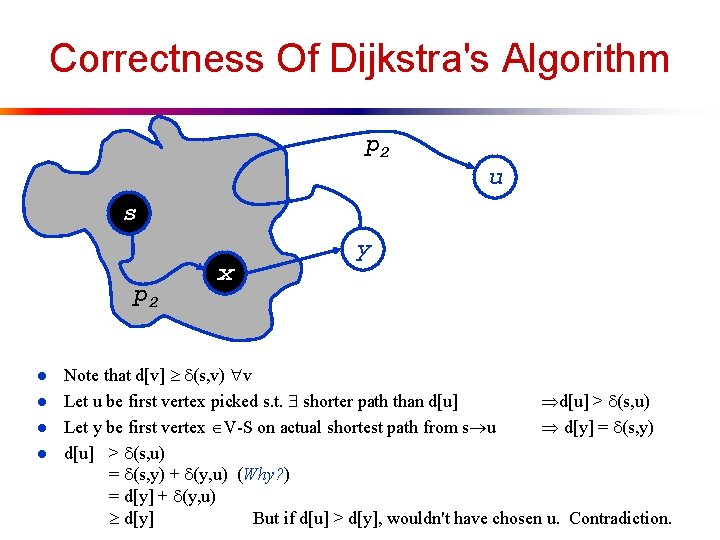
Correctness Of Dijkstra's Algorithm p 2 u s p 2 l l x y Note that d[v] (s, v) v Let u be first vertex picked s. t. shorter path than d[u] > (s, u) Let y be first vertex V-S on actual shortest path from s u d[y] = (s, y) d[u] > (s, u) = (s, y) + (y, u) (Why? ) = d[y] + (y, u) d[y] But if d[u] > d[y], wouldn't have chosen u. Contradiction.

The End