Shortest paths Algorithms and Networks Shortest paths Contents

Shortest paths Algorithms and Networks: Shortest paths

Contents • The shortest path problem: – Statement – Versions • Applications • Algorithms (for single source sp problem) – Reminders: relaxation, Dijkstra, Variants of Dijkstra, Bellman-Ford, Johnson … – Scaling technique (Gabow’s algorithm) • Variant algorithms: A*, bidirectional search • Bottleneck shortest paths 2 Algorithms and Networks: Shortest paths

Notation • In the entire course: – n = |V|, the number of vertices – m = |E| or m = |A|, the number of edges or the number of arcs 3 Algorithms and Networks: Shortest paths

1 Definition and Applications 4 Algorithms and Networks: Shortest paths

Shortest path problem • (Directed) graph G=(V, E), length for each edge e in E, w(e) • Distance from u to v: length of shortest path from u to v • Shortest path problem: find distances, find shortest paths … 5 • Versions: – – – All pairs Single pair Single source Single destination Lengths can be • All equal (unit lengths) (BFS) • Non-negative • Negative but no negative cycles • Negative cycles possible Algorithms and Networks: Shortest paths

Notations • dw(s, t): distance of s to t: length of shortest path from s to t when using edge length function w • d(s, t): the same, but w is clear from context • d(s, s) = 0: we always assume there is a path with 0 edges from a vertex to itself: s 6 Algorithms and Networks: Shortest paths

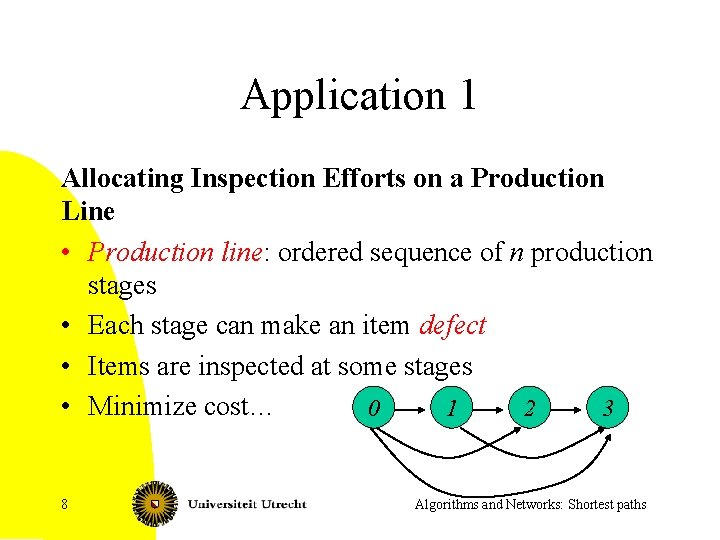
Applications • • 7 Subroutine in other graph algorithms Route planning Difference constraints Allocating Inspection Effort on a Production Line Algorithms and Networks: Shortest paths

Application 1 Allocating Inspection Efforts on a Production Line • Production line: ordered sequence of n production stages • Each stage can make an item defect • Items are inspected at some stages • Minimize cost… 0 1 2 3 8 Algorithms and Networks: Shortest paths

Allocating Inspection Efforts on a Production Line • Production line: ordered sequence of n production stages. • Items are produced in batches of B > 0 items. • Probability that stage i produces a defect item is ai. • Manufacturing cost per item at stage i: pi. • Cost of inspecting at stage j, when last inspection has been done at stage i: – fij per batch, plus – gij per item in the batch • When should we inspect to minimize total costs? 9 Algorithms and Networks: Shortest paths

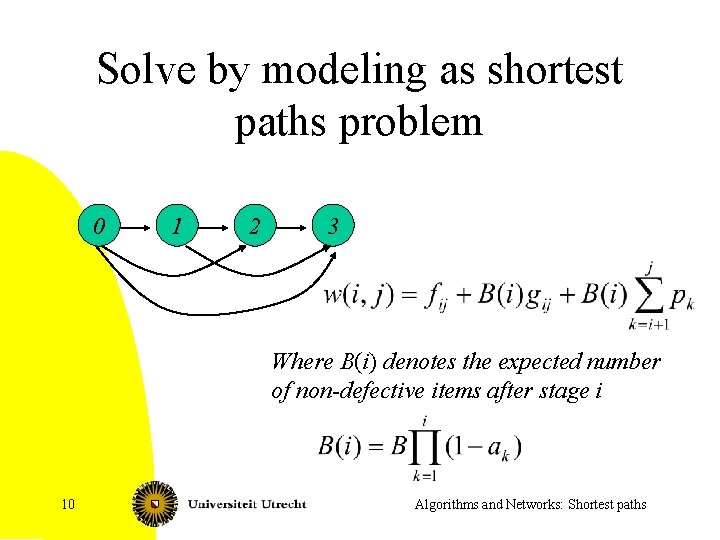
Solve by modeling as shortest paths problem 0 1 2 3 Where B(i) denotes the expected number of non-defective items after stage i 10 Algorithms and Networks: Shortest paths

Idea behind model • w(i, j) is the cost of production and inspection from stage i to stage j, assuming we inspect at stage i, and then again at stage j • Find the shortest path from 0 to n 11 Algorithms and Networks: Shortest paths

Application 2: Difference constraints • Tasks with precedence constraints and running length • Each task i has – Time to complete bi > 0 • Some tasks can be started after other tasks have been completed: – Constraint: sj + bj £ si • First task can start at time 0. When can we finish last task? • Shortest paths problem on directed acyclic graphs (see next dias)! 12 Algorithms and Networks: Shortest paths

Model • • Take vertex for each task Take special vertex v 0 Vertex v 0 models time 0 Arc (v 0, i) for each task vertex i, with length 0 • For each precedence constraint sj + bj £ si an arc (j, i) with length bj 13 Algorithms and Networks: Shortest paths

Long paths give time lower bounds • If there is a path from v 0 to vertex i with length x, then task i cannot start before time x • Proof with induction. . . • Optimal: start each task i at time equal to length of longest path from v 0 to i. – This gives a valid scheme, and it is optimal by the solution 14 Algorithms and Networks: Shortest paths

Difference constraints as shortest paths • The longest path problem can be solved in O(n+m) time, as we have a directed acyclic graph. • Transforming to shortest paths problem: multiply all lengths and times by – 1. 15 Algorithms and Networks: Shortest paths

2 Algorithms for shortest path problems (reminders) 16 Algorithms and Networks: Shortest paths

Basis of single source algorithms • Source s. • Each vertex v has variable D[v] – Invariant: d(s, v) £ D[v] for all v – Initially: D[s]=0; v¹ s: D[v] = ¥ • Relaxation step over edge (u, v): – D[v] = min { D[v], D[u]+ w(u, v) } 17 Algorithms and Networks: Shortest paths

Maintaining shortest paths • Each vertex maintains a pointer to the `previous vertex on the current shortest path’ (sometimes NIL): p(v) p-values build • Initially: p(v) = NIL for each v paths of length D(v) Shortest paths tree • Relaxation step becomes: Relax (u, v, w) If D[v] > D[u]+ w(u, v) then D[v] = D[u] + w(u, v); p(v) = u 18 Algorithms and Networks: Shortest paths

Dijkstra • Initialize • Take priority queue Q, initially containing all vertices • While Q is not empty, – Select vertex v from Q of minimum value D[v] – Relax across all outgoing edges from v • Note: each relaxation cause a change of a Dvalue and thus a change in the priority queue • This happens at most |E| times 19 Algorithms and Networks: Shortest paths

On Dijkstra • Assumes all lengths are non-negative • Correctness proof (done in `Algoritmiek’) • Running time: – Depends on implementation of priority queue • • 20 O(n 2): standard queue O(m + n log n): Fibonacci heaps O((m + n) log n): red-black trees, heaps … Algorithms and Networks: Shortest paths

Negative lengths • What if w(u, v) < 0? • Negative cycles, reachable from s … • Bellman-Ford algorithm: – For instances without negative cycles: • In O(nm) time: SSSP problem when no negative cycles reachable from s • Also: detects negative cycle 21 Algorithms and Networks: Shortest paths

Bellman-Ford • Initialize • Repeat |V|-1 times: Clearly: O(nm) time – For every edge (u, v) in E do: Relax(u, v, w) • For every edge (u, v) in E do If D[v] > D[u] + w(u, v) then There exists a negative circuit! Stop • There is no negative circuit, and for all vertices v: D[v] = d(s, v). 22 Algorithms and Networks: Shortest paths

Correctness of Bellman-Ford • Invariant: If no negative cycle is reachable from s, then after i runs of main loop, we have: – If there is a shortest path from s to u with at most i edges, then D[u]=d[s, u], for all u. • If no negative cycle reachable from s, then every vertex has a shortest path with at most n – 1 edges. • If a negative cycle reachable from s, then there will always be an edge with a relaxation possible. 23 Algorithms and Networks: Shortest paths

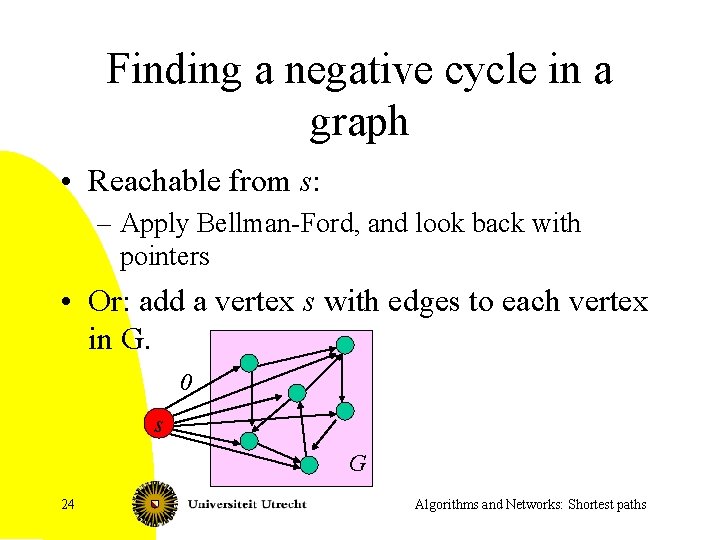
Finding a negative cycle in a graph • Reachable from s: – Apply Bellman-Ford, and look back with pointers • Or: add a vertex s with edges to each vertex in G. 0 s G 24 Algorithms and Networks: Shortest paths

All pairs • Dynamic programming: O(n 3) (Floyd, 1962) • Johnson: improvement for sparse graphs with reweighting technique: – O(n 2 log n + nm) time. – Works if no negative cycles – Observation: if all weights are non-negative we can run Dijkstra with each vertex as starting vertex: that gives O(n 2 log n + nm) time. – What if we have negative lengths: reweighting… 25 Algorithms and Networks: Shortest paths

Reweighting • Let h: V ® R be any function to the reals. • Write wh(u, v) = w(u, v) + h(u) – h(v). • Lemmas: – Let P be a path from x to y. Then: wh(P) = w(P) + h(x) – h(y). – dh(x, y) = d(x, y) + h(x) – h(y). – P is a shortest path from x to y with lengths w, if and only if it is so with lengths wh. – G has a negative-length circuit with lengths w, if and only if it has a negative-length circuit with lengths wh. 26 Algorithms and Networks: Shortest paths

What height function h is good? • Look for height function h with – wh(u, v) ³ 0, for all edges (u, v). • If so, we can: – Compute wh(u, v) for all edges. – Run Dijkstra but now with wh(u, v). • Special method to make h with a SSSP problem, and Bellman-Ford. 27 Algorithms and Networks: Shortest paths

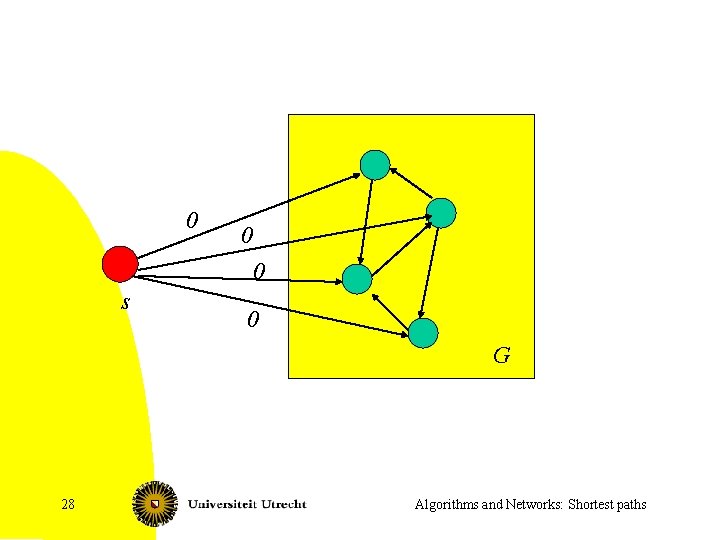
0 0 0 s 0 G 28 Algorithms and Networks: Shortest paths

Choosing h • Set h(v) = d(s, v) (in new graph) • Solving SSSP problem with negative edge lengths; use Bellman-Ford. • If negative cycle detected: stop. • Note: for all edges (u, v): wh(u, v) = w(u, v) + h(u) – h(v) = w(u, v) + d(s, u) – d(s, v) ³ 0 29 Algorithms and Networks: Shortest paths

Johnson’s algorithm • Build graph G’ (as shown) • Compute with Bellman-Ford d(s, v) for all v • Set wh(u, v) = w(u, v) + d. G’(s, u) – d. G’ (s, v) for all edges (u, v). O(n 2 log n + nm) time • For all u do: – Use Dijkstra’s algorithm to compute dh(u, v) for all v. – Set d(u, v) = dh(u, v) + d. G’(s, v) – d. G’(s, u). 30 Algorithms and Networks: Shortest paths

3 Shortest path algorithms “using the numbers” and scaling 31 Algorithms and Networks: Shortest paths

Using the numbers • Back to the single source shortest paths problem with non-negative distances – Suppose D is an upper bound on the maximum distance from s to a vertex v. – Let L be the largest length of an edge. – Single source shortest path problem is solvable in O(m + D) time. 32 Algorithms and Networks: Shortest paths

In O(m+D) time • Keep array of doubly linked lists: L[0], …, L[D], • Maintain that for v with D[v] £ D, – v in L[D[v]]. • Keep a current minimum m. – Invariant: all L[k] with k < m are empty • Changing D[v] from x to y: take v from L[x] (with pointer), and add it to L[y]: O(1) time each. • Extract min: while L[m] empty, m++; then take the first element from list L[m]. • Total time: O(m+D) 33 Algorithms and Networks: Shortest paths

Corollary and extension • SSSP: in O(m+n. L) time. (Take D=n. L). • Gabow (1985): SSSP problem can be solved in O(m log. R L) time, where – R = max{2, m/n} – L : maximum length of edge • Gabow’s algorithm uses scaling technique! 34 Algorithms and Networks: Shortest paths

Gabow’s algorithm Main idea • First, build a scaled instance: – For each edge e set w’(e) = ë w(e) / R û. • Recursively, solve the scaled instance. • Another shortest paths instance can be used to compute the correction terms! 35 Algorithms and Networks: Shortest paths

How far are we off? • We want d(s, v) • R * dw’(s, v) is when we scale back our scaled instance: what error did we make when rounding? • Set for each edge (x, y) in E: – Z(x, y) = w(x, y) – R* dw’(s, x) + R * dw’(s, y) • Works like height function, so the same shortest paths! • Height of x is – R * dw’(s, x) 36 Algorithms and Networks: Shortest paths

A claim • For all vertices v in V: – d(s, v) = d. Z(s, v) + R * dw’(s, v) • As with height functions (telescope): – d(s, v) = d. Z(s, v) + h(s) – h(v) = d. Z(s, v) – R*dw’(s, s) + R * dw’(s, v) – And dw’(s, s) = 0 • Thus, we can compute distances for w by computing distances for Z and for w’ 37 Algorithms and Networks: Shortest paths

Gabow’s algorithm If L <= R, then • solve the problem using the O(m+n. R) algorithm (Base case) Else • For each edge e: set w’(e) = ë w(e) / R û. • Recursively, compute the distances but with the new length function w’. Set for each edge (u, v): – Z(u, v) = w(u, v) + R* dw’(s, u) – R * dw’(s, v). • Compute d. Z(s, v) for all v (how? See next!) and then use – d(s, v) = d. Z(s, v) + R * dw’(s, v) 38 Algorithms and Networks: Shortest paths

A property of Z • For each edge (u, v) Î E we have: – Z(u, v) = w(u, v) + R* dw’(s, u) – R * dw’(s, v) ³ 0, because – w(u, v) ³ R * w’(u, v) ³ R * (dw’(s, v) – dw’(s, u)). • So, a variant of Dijkstra can be used to compute distances for Z. 39 Algorithms and Networks: Shortest paths

Computing distances for Z • For each vertex v we have – d. Z(s, v) £ n. R for all v reachable from s • • Consider a shortest path P for distance function w’ from s to v For each of the less than n edges e on P, w(e) £ R + R*w’(e) So, d(s, v) £ w(P) £ n. R + R* w’(P) = n. R + R* dw’(s, v) Use that d(s, v) = d. Z(s, v) + R * dw’(s, v) • So, we can use O(m+ n. R) algorithm (Dijkstra with doubly-linked lists) to compute all values d. Z(v). 40 Algorithms and Networks: Shortest paths

Gabow’s algorithm (analysis) • Recursive step: costs O( m log. R L’) with L’= ë L/R û. • SSSP for Z costs O(m + n. R) = O(m). • Note: log. R L’ £ (log. R L) – 1. • So, Gabow’s algorithm uses O(m log. R L) time. 41 Algorithms and Networks: Shortest paths

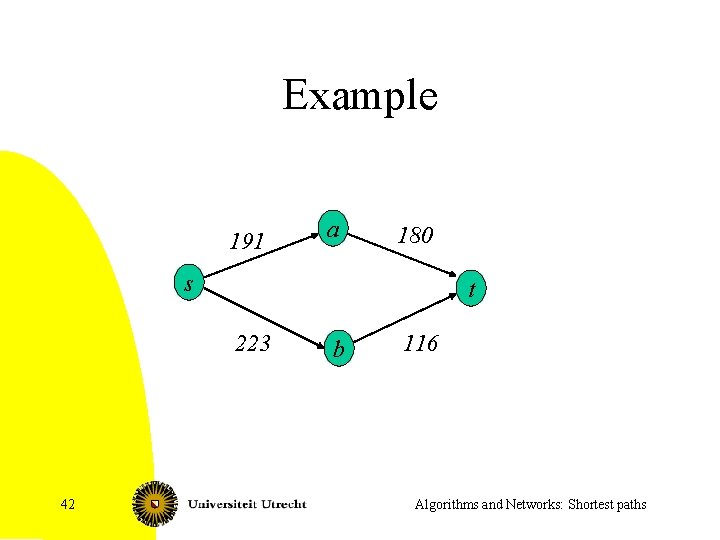
Example 191 a 180 s t 223 42 b 116 Algorithms and Networks: Shortest paths

4 Variants: A* and bidirectional search 43 Algorithms and Networks: Shortest paths

A* • Practical heuristic for shortest paths • Consider shortest paths in geometric setting (e. g. , routeplanning for cars system) • Standard Dijkstra would explore many paths that are clearly in the wrong direction – Utrecht to Groningen would look at roads near Den Bosch or even Maastricht 44 Algorithms and Networks: Shortest paths

A heuristic for the distance to the target • Suppose we have a heuristic h that approximates the distance to target t • Example: Euclidean distance on the plane of the points – Somewhat smaller than the real distance, but looks reasonable 45 Algorithms and Networks: Shortest paths

Admissible and consistent • h is admissible if for each vertex v: h(v) <= d(v, t) • h is consistent if for each edge (v, w) in E: h(v) <= h(w) + l(x, y) 46 Algorithms and Networks: Shortest paths

A* algorithm as shortest paths with height function • Use h as a height function, i. e. , set for each edge (v, w): lh(v, w) = l(v, w) – h(v)+h(w) • Telescope rule … • Consistent: all new lengths are non-negative • Admissible: no fear of stopping too early • Note: arcs in wrong direction are less frequently used • Faster algorithm; still correct 47 Algorithms and Networks: Shortest paths

Bidirectional search • For a single pair shortest path problem: • Start a Dijkstra-search from both sides simultaneously • Analysis needed for stopping criterion • Faster in practice • Combines nicely with A* s 48 t s t Algorithms and Networks: Shortest paths

5 Bottleneck shortest paths 49 Algorithms and Networks: Shortest paths

Bottleneck shortest path • Given: weighted graph G, weight w(e) for each arc, vertices s, t. • Problem: find a path from s to t such that the maximum weight of an arc on the path is as small as possible. – Or, reverse: such that the minimum weight is as large as possible: maximum capacity path 50 Algorithms and Networks: Shortest paths

Algorithms • On directed graphs: O((m+n) log m), – Or: O((m+n) log L) with L the maximum absolute value of the weights – Binary search and DFS • On undirected graphs: O(m+n) with divide and conquer strategy 51 Algorithms and Networks: Shortest paths

Bottleneck shortest paths on undirected graphs • Find the median weight of all weights of edges, say r. • Look to graph Gr formed by edges with weight at most r. • If s and t in same connected component of Gr, then the bottleneck is at most r: now remove all edges with weight more than r, and repeat (recursion). • If s and t in different connected components of Gr: the bottleneck is larger than r. Now, contract all edges with weight at most r, and recurse. • T(m) = O(m) + T(m/2) 52 Algorithms and Networks: Shortest paths

5 Conclusions 53 Algorithms and Networks: Shortest paths

Conclusions • Applications • Several algorithms for shortest paths – Variants of the problem – Detection of negative cycles – Reweighting technique – Scaling technique • A*, bidirectional • Bottleneck shortest paths 54 Algorithms and Networks: Shortest paths