Eager Prim Dijkstra Minimum spanning tree Minimum spanning

Eager Prim Dijkstra

Minimum spanning tree • Minimum spanning tree (MST) • is a spanning tree whose weight is not larger than any other spanning tree • Prim v. s. Kruskal • Prim: • At each time, add an edge connecting tree vertex and non-tree vertex • Minimum-weight crossing edge • Min. PQ, Index. Min. PQ • Kruskal • gradually add minimum-weight edge to the MST, avoid forming cycle • Union-find, Min. PQ

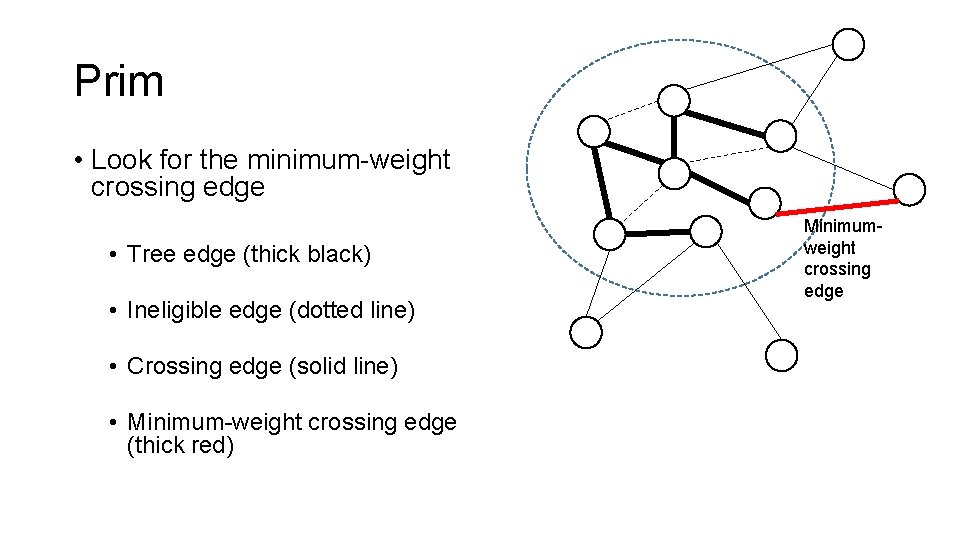
Prim • Look for the minimum-weight crossing edge • Tree edge (thick black) • Ineligible edge (dotted line) • Crossing edge (solid line) • Minimum-weight crossing edge (thick red) Minimumweight crossing edge

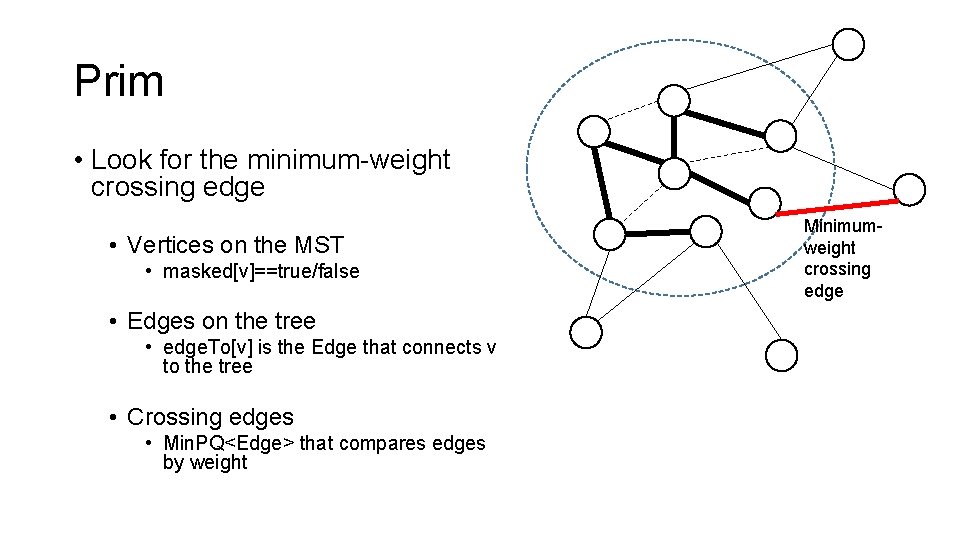
Prim • Look for the minimum-weight crossing edge • Vertices on the MST • masked[v]==true/false • Edges on the tree • edge. To[v] is the Edge that connects v to the tree • Crossing edges • Min. PQ<Edge> that compares edges by weight Minimumweight crossing edge

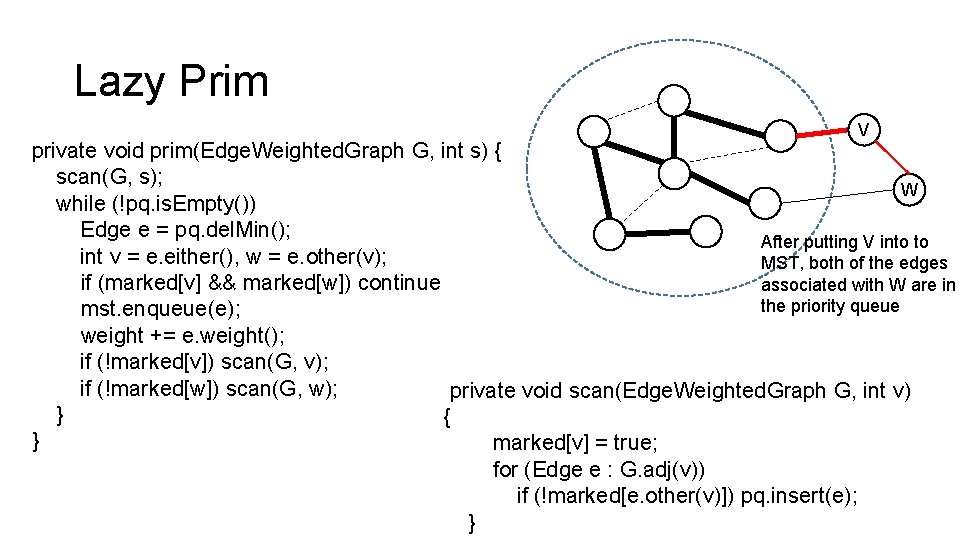
Lazy Prim V private void prim(Edge. Weighted. Graph G, int s) { scan(G, s); W while (!pq. is. Empty()) Edge e = pq. del. Min(); After putting V into to int v = e. either(), w = e. other(v); MST, both of the edges if (marked[v] && marked[w]) continue associated with W are in the priority queue mst. enqueue(e); weight += e. weight(); if (!marked[v]) scan(G, v); if (!marked[w]) scan(G, w); private void scan(Edge. Weighted. Graph G, int v) } { } marked[v] = true; for (Edge e : G. adj(v)) if (!marked[e. other(v)]) pq. insert(e); }

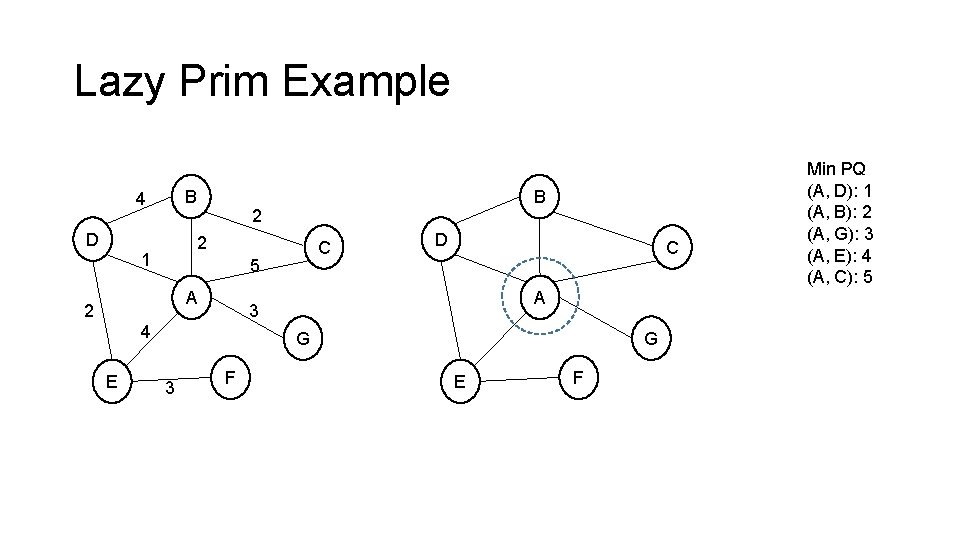
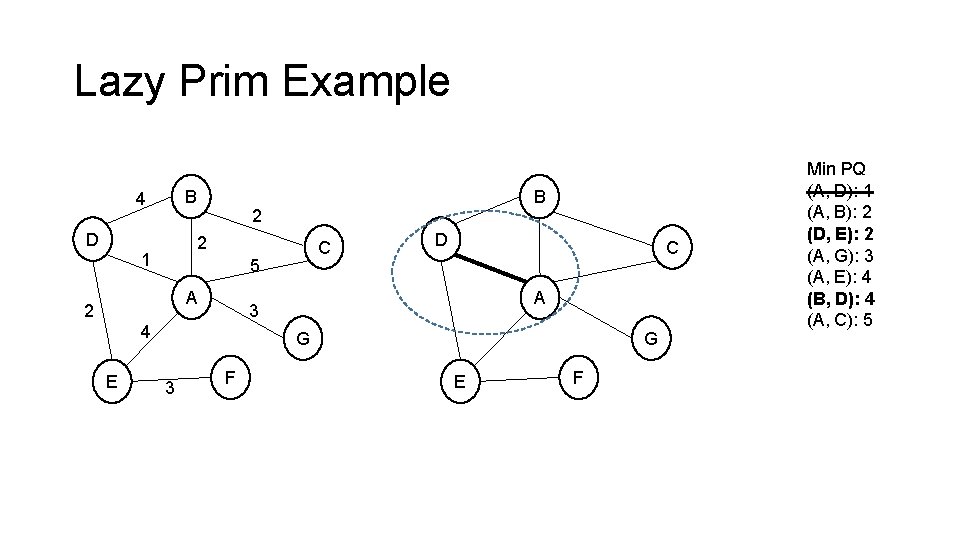
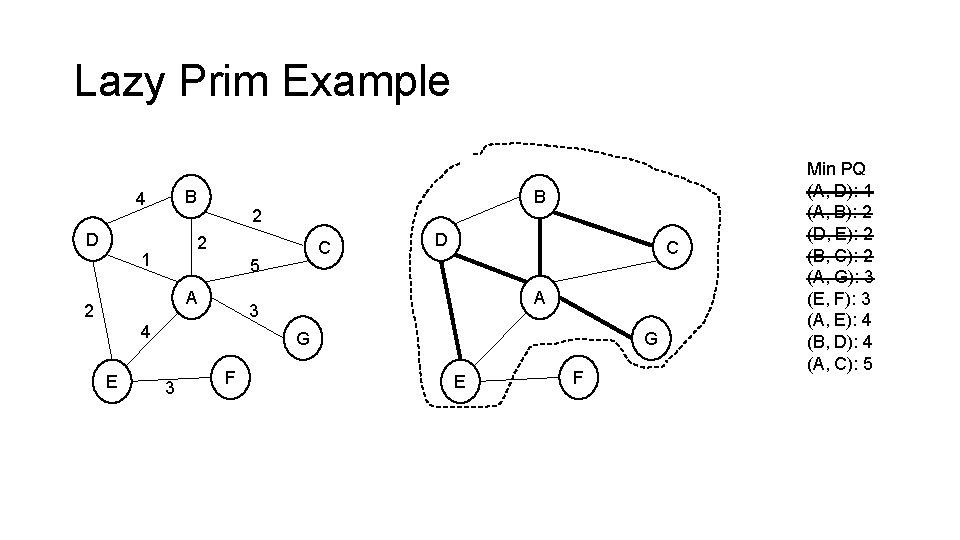
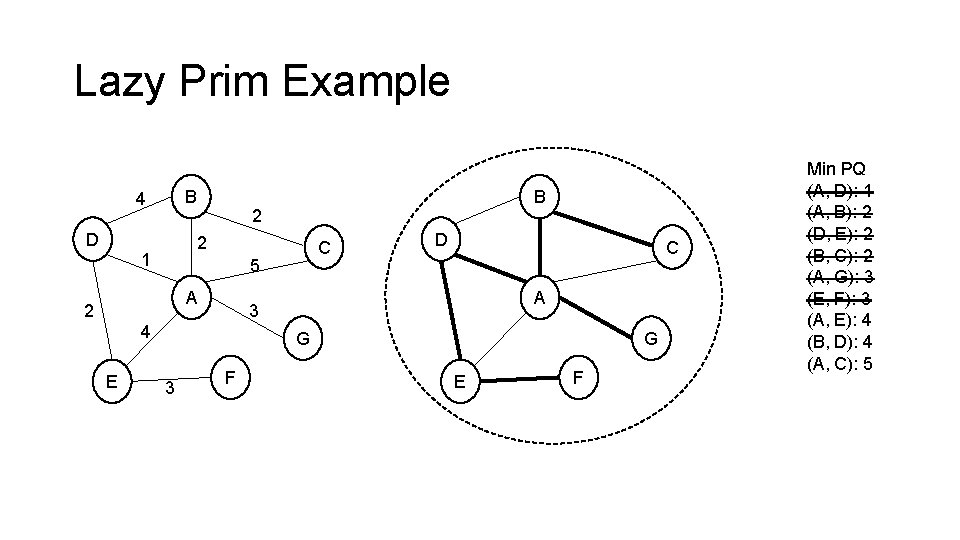
Lazy Prim Example B 4 D 2 2 1 C 5 A 2 D C A 3 4 E B G 3 F G E F Min PQ (A, D): 1 (A, B): 2 (A, G): 3 (A, E): 4 (A, C): 5

Lazy Prim Example B 4 D 2 2 1 C 5 A 2 D C A 3 4 E B G 3 F G E F Min PQ (A, D): 1 (A, B): 2 (D, E): 2 (A, G): 3 (A, E): 4 (B, D): 4 (A, C): 5

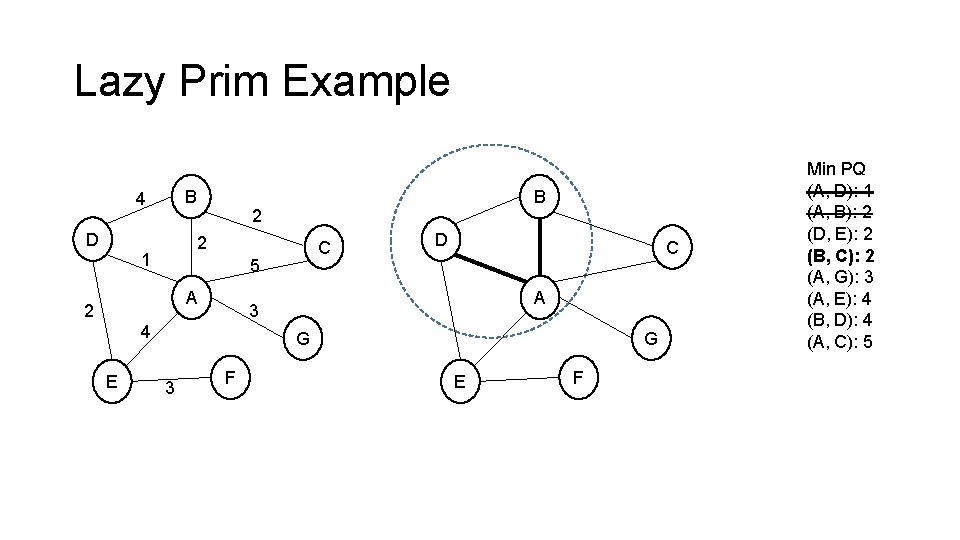
Lazy Prim Example B 4 D 2 2 1 C 5 A 2 D C A 3 4 E B G 3 F G E F Min PQ (A, D): 1 (A, B): 2 (D, E): 2 (B, C): 2 (A, G): 3 (A, E): 4 (B, D): 4 (A, C): 5

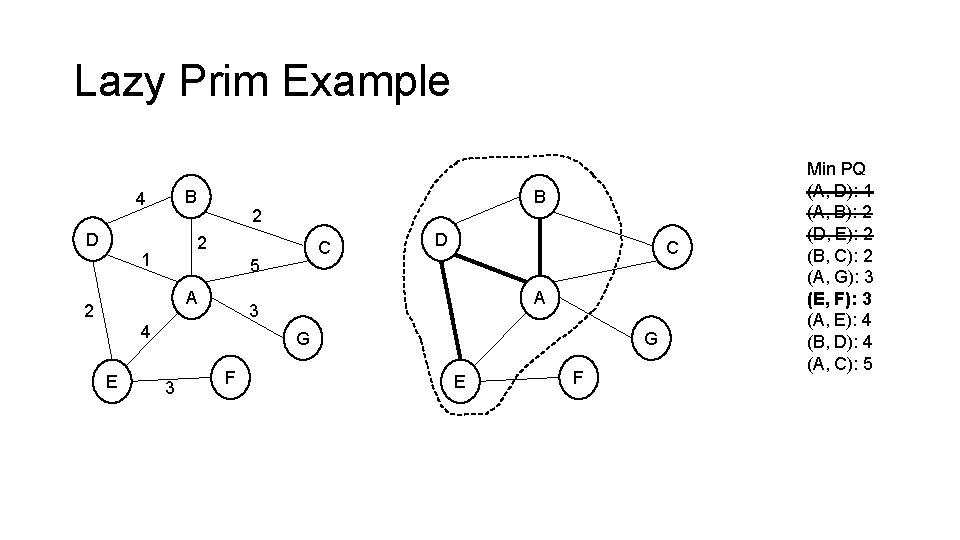
Lazy Prim Example B 4 D 2 2 1 C 5 A 2 D C A 3 4 E B G 3 F G E F Min PQ (A, D): 1 (A, B): 2 (D, E): 2 (B, C): 2 (A, G): 3 (E, F): 3 (A, E): 4 (B, D): 4 (A, C): 5

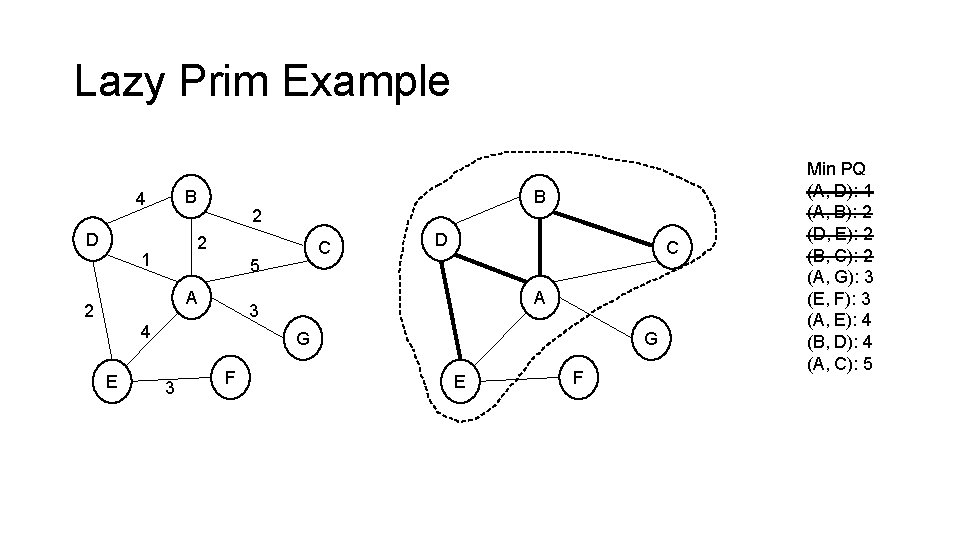
Lazy Prim Example B 4 D 2 2 1 C 5 A 2 D C A 3 4 E B G 3 F G E F Min PQ (A, D): 1 (A, B): 2 (D, E): 2 (B, C): 2 (A, G): 3 (E, F): 3 (A, E): 4 (B, D): 4 (A, C): 5

Lazy Prim Example B 4 D 2 2 1 C 5 A 2 D C A 3 4 E B G 3 F G E F Min PQ (A, D): 1 (A, B): 2 (D, E): 2 (B, C): 2 (A, G): 3 (E, F): 3 (A, E): 4 (B, D): 4 (A, C): 5

Lazy Prim Example B 4 D 2 2 1 C 5 A 2 D C A 3 4 E B G 3 F G E F Min PQ (A, D): 1 (A, B): 2 (D, E): 2 (B, C): 2 (A, G): 3 (E, F): 3 (A, E): 4 (B, D): 4 (A, C): 5

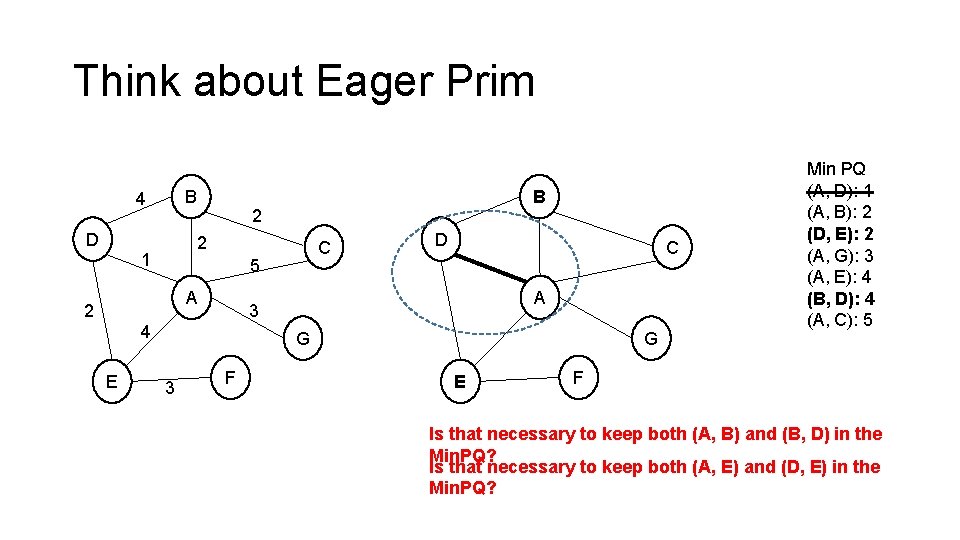
Think about Eager Prim • Lazy Prim • elge • Textbook implementation (quiz answer) • vlge (simple optimization) • For a graph which has v node, there are v-1 edges in the spanning tree • while (!pq. is. Empty()) • // break the loop if there is already v-1 edges in the MST • Eager Prim • vlgv • v edges in the Min. PQ instead of e edges • How?

Think about Eager Prim B 4 D 2 2 1 C 5 A 2 D C A 3 4 E B G 3 F G E Min PQ (A, D): 1 (A, B): 2 (D, E): 2 (A, G): 3 (A, E): 4 (B, D): 4 (A, C): 5 F Is that necessary to keep both (A, B) and (B, D) in the Min. PQ? Is that necessary to keep both (A, E) and (D, E) in the Min. PQ?

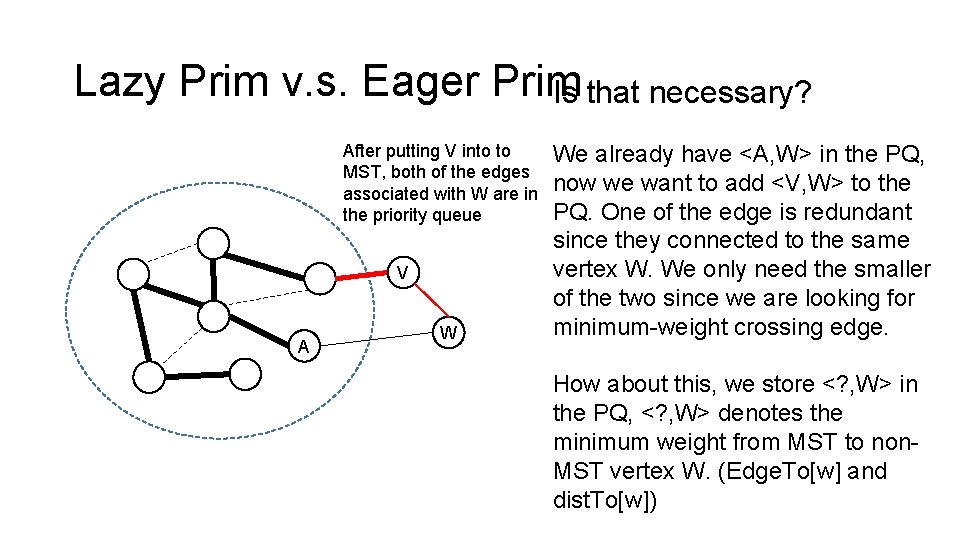
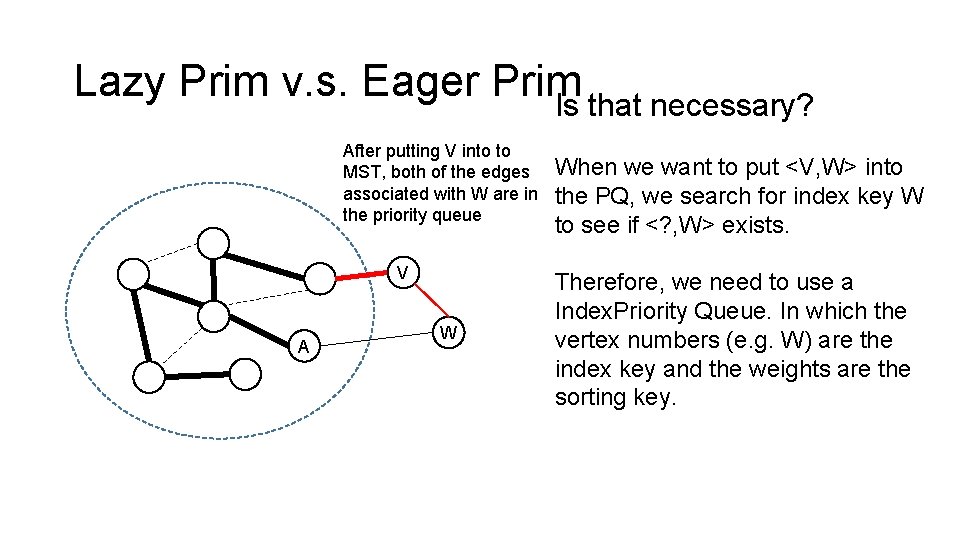
Lazy Prim v. s. Eager Prim Is that necessary? After putting V into to MST, both of the edges associated with W are in the priority queue V A W We already have <A, W> in the PQ, now we want to add <V, W> to the PQ. One of the edge is redundant since they connected to the same vertex W. We only need the smaller of the two since we are looking for minimum-weight crossing edge. How about this, we store <? , W> in the PQ, <? , W> denotes the minimum weight from MST to non. MST vertex W. (Edge. To[w] and dist. To[w])

Lazy Prim v. s. Eager Prim Is that necessary? After putting V into to MST, both of the edges associated with W are in the priority queue V A W When we want to put <V, W> into the PQ, we search for index key W to see if <? , W> exists. Therefore, we need to use a Index. Priority Queue. In which the vertex numbers (e. g. W) are the index key and the weights are the sorting key.

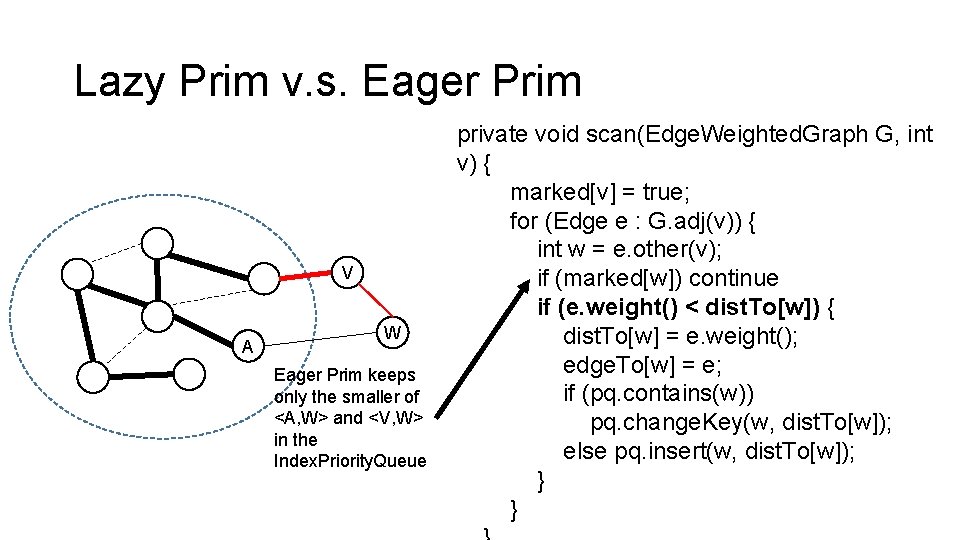
Lazy Prim v. s. Eager Prim V A W Eager Prim keeps only the smaller of <A, W> and <V, W> in the Index. Priority. Queue private void scan(Edge. Weighted. Graph G, int v) { marked[v] = true; for (Edge e : G. adj(v)) { int w = e. other(v); if (marked[w]) continue if (e. weight() < dist. To[w]) { dist. To[w] = e. weight(); edge. To[w] = e; if (pq. contains(w)) pq. change. Key(w, dist. To[w]); else pq. insert(w, dist. To[w]); } }

Eager Prim public Prim. MST(Edge. Weighted. Graph G) { edge. To = new Edge[G. V()]; dist. To = new double[G. V()]; marked = new boolean[G. V()]; pq = new Index. Min. PQ<Double>(G. V()); for (int v = 0; v < G. V(); v++) dist. To[v] = Double. POSITIVE_INFINITY; for (int v = 0; v < G. V(); v++) if (!marked[v]) prim(G, v); assert check(G); } private void prim(Edge. Weighted. Graph G, int s) { dist. To[s] = 0. 0; pq. insert(s, dist. To[s]); while (!pq. is. Empty()) { int v = pq. del. Min(); scan(G, v); } } private void scan(Edge. Weighted. Graph G, int v) { marked[v] = true; for (Edge e : G. adj(v)) { int w = e. other(v); if (marked[w]) continue if (e. weight() < dist. To[w]) { dist. To[w] = e. weight(); edge. To[w] = e; if (pq. contains(w)) pq. change. Key(w, dist. To[w]); else pq. insert(w, dist. To[w]); } } }

Dijkstra • Similar idea is used in Dijkstra algorithm • Dijkstra • Digraph • Single-source shortest paths

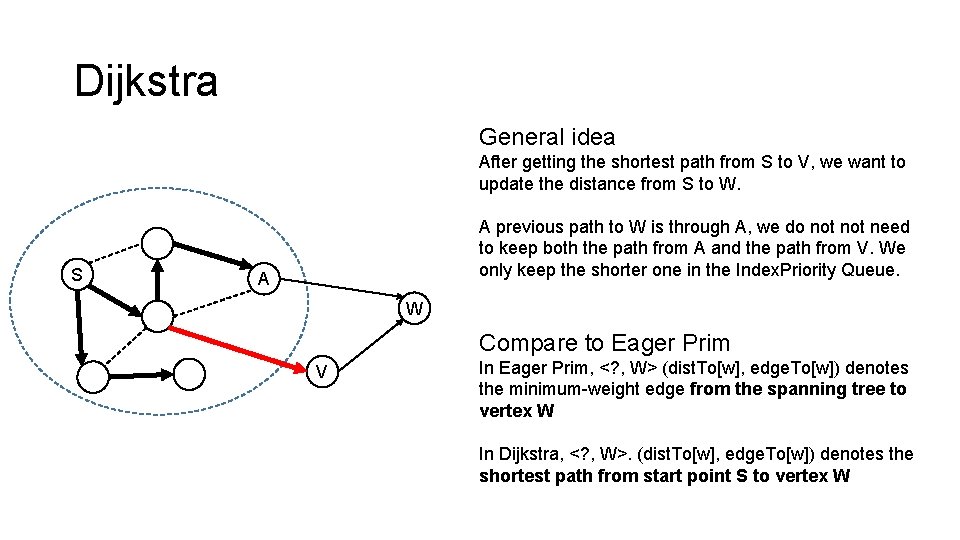
Dijkstra General idea After getting the shortest path from S to V, we want to update the distance from S to W. S A previous path to W is through A, we do not need to keep both the path from A and the path from V. We only keep the shorter one in the Index. Priority Queue. A W Compare to Eager Prim V In Eager Prim, <? , W> (dist. To[w], edge. To[w]) denotes the minimum-weight edge from the spanning tree to vertex W In Dijkstra, <? , W>. (dist. To[w], edge. To[w]) denotes the shortest path from start point S to vertex W

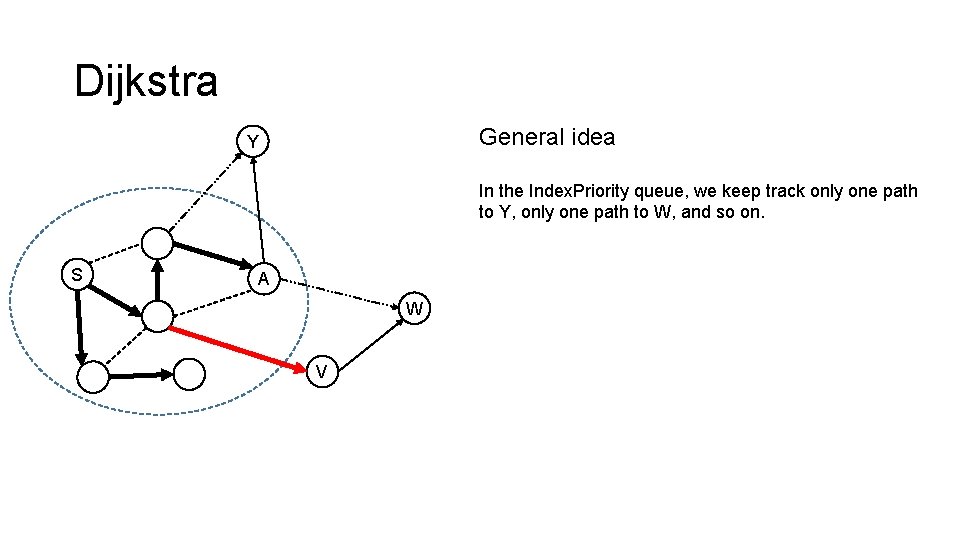
Dijkstra General idea Y In the Index. Priority queue, we keep track only one path to Y, only one path to W, and so on. S A W V

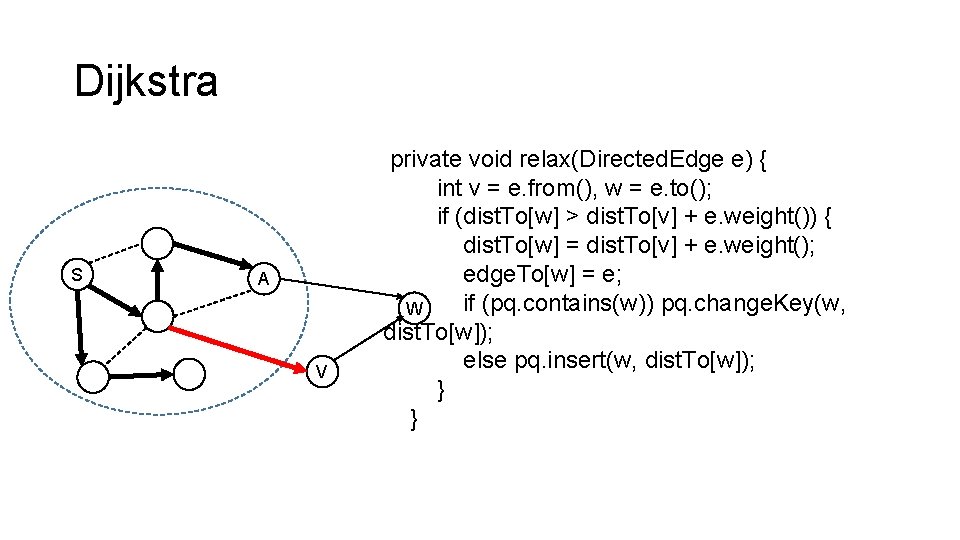
Dijkstra S A V private void relax(Directed. Edge e) { int v = e. from(), w = e. to(); if (dist. To[w] > dist. To[v] + e. weight()) { dist. To[w] = dist. To[v] + e. weight(); edge. To[w] = e; if (pq. contains(w)) pq. change. Key(w, W dist. To[w]); else pq. insert(w, dist. To[w]); } }

Prim MST v. s. Dijkstra private void scan(Edge. Weighted. Graph G, int v) { private void relax(Directed. Edge e) { marked[v] = true; int v = e. from(), w = e. to(); for (Edge e : G. adj(v)) { if (dist. To[w] > dist. To[v] + e. weight()) { int w = e. other(v); dist. To[w] = dist. To[v] + e. weight(); if (marked[w]) continue edge. To[w] = e; if (e. weight() < dist. To[w]) { if (pq. contains(w)) pq. change. Key(w, dist. To[w]) dist. To[w] = e. weight(); else pq. insert(w, dist. To[w]); edge. To[w] = e; if (pq. contains(w)) pq. change. Key(w, dist. To[w]); } } else pq. insert(w, dist. To[w]); } } } In Dijsktra, dist. To[w] stores the minimum-weight In Prim, dist. To[w] stores the minimum-weight crossing edge connecting MST vertex to non-MST from single source point S to non-explored vertex W. This is a acummulated value. vertex W