Minimum Spanning Trees Definition A Minimum Spanning Tree

Definition • A Minimum Spanning Tree (MST) is a subgraph of an undirected graph

Algorithm Characteristics • Both Prim’s and Kruskal’s Algorithms work with undirected graphs • Both

Prim’s Algorithm • Similar to Dijkstra’s Algorithm except that dv records edge weights, not

Walk-Through 2 F 10 A 3 7 4 H 18 B 9 C 3

Kruskal’s Algorithm • Work with edges, rather than nodes • Two steps: – Sort

Select first |V|– 1 edges which do not generate a cycle F 10 A

Select first |V|– 1 edges which do not generate a cycle 3 F A

Detecting Cycles • Use Disjoint Sets (Chapter 8)

Slides: 41

Download presentation

Minimum Spanning Trees

Definition • A Minimum Spanning Tree (MST) is a subgraph of an undirected graph such that the subgraph spans (includes) all nodes, is connected, is acyclic, and has minimum total edge weight

Algorithm Characteristics • Both Prim’s and Kruskal’s Algorithms work with undirected graphs • Both work with weighted and unweighted graphs but are more interesting when edges are weighted • Both are greedy algorithms that produce optimal solutions

Prim’s Algorithm • Similar to Dijkstra’s Algorithm except that dv records edge weights, not path lengths

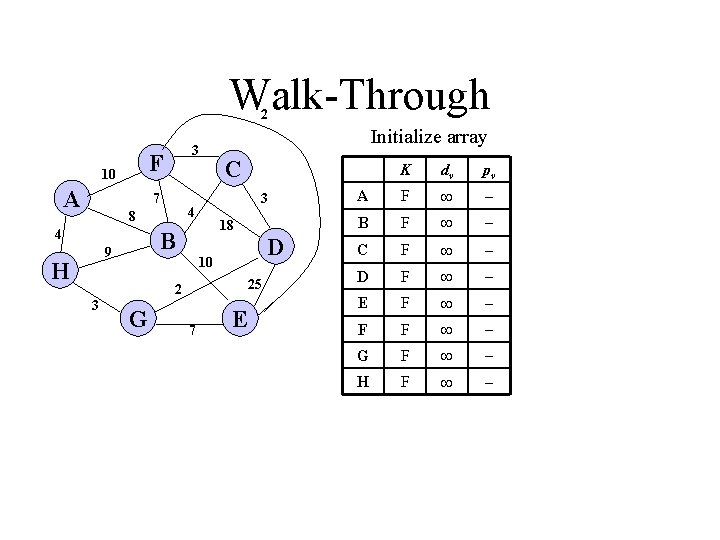
Walk-Through 2 F 10 A 3 7 4 H 18 B 9 C 3 4 8 Initialize array 25 2 3 D 10 G 7 E K dv pv A F B F C F D F E F F F G F H F

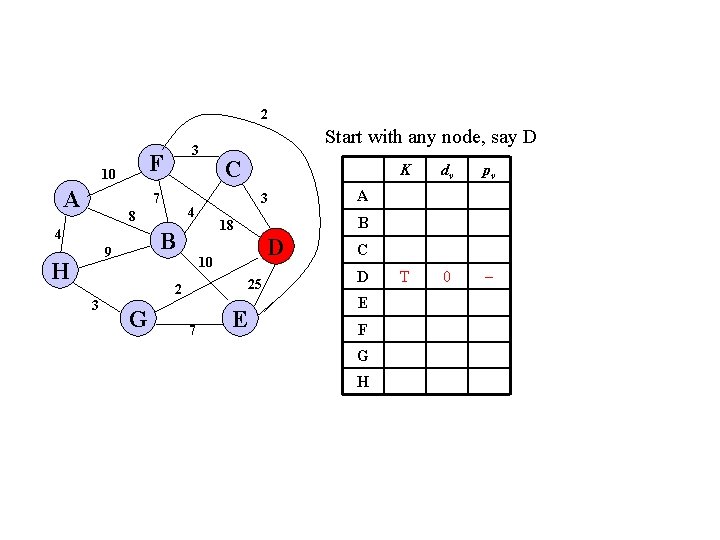
2 F 10 A 3 7 4 H 3 D 10 25 2 G 7 E K dv pv T 0 A B 18 B 9 C 3 4 8 Start with any node, say D C D E F G H

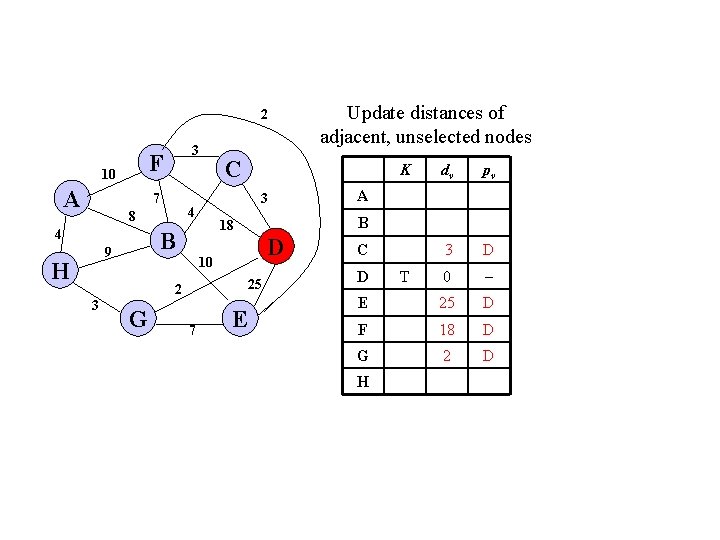
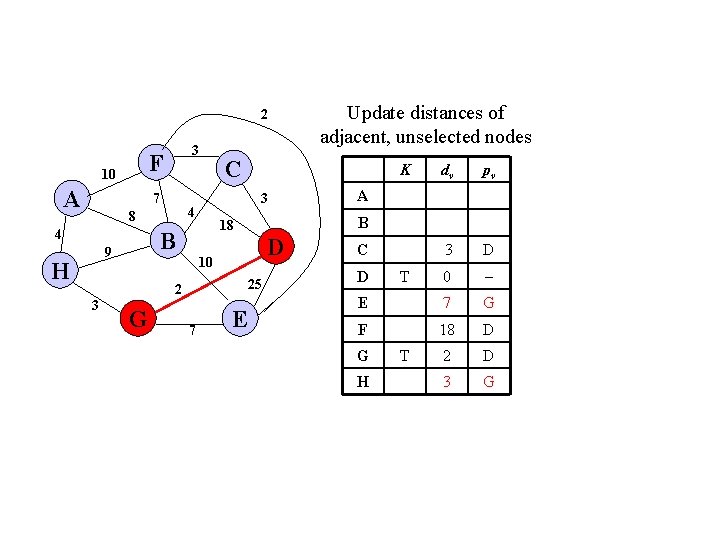
2 F 10 A 3 7 4 H G D 25 7 E dv pv 3 D 0 E 25 D F 18 D G 2 D A B 10 2 3 K 18 B 9 C 3 4 8 Update distances of adjacent, unselected nodes C D H T

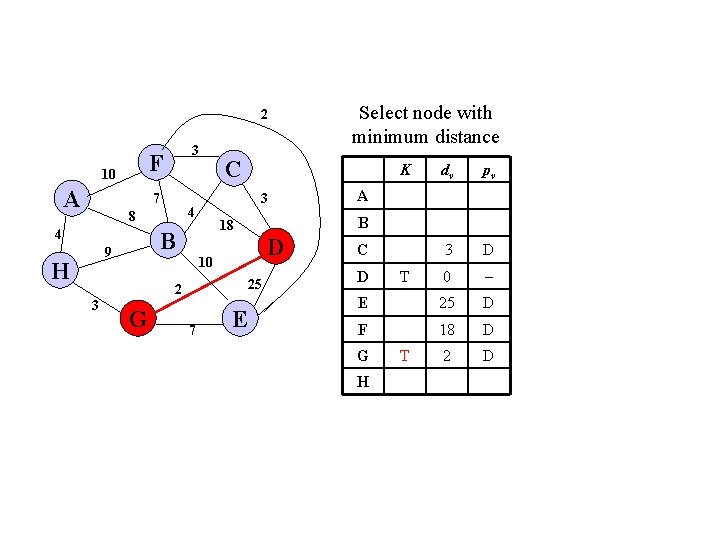
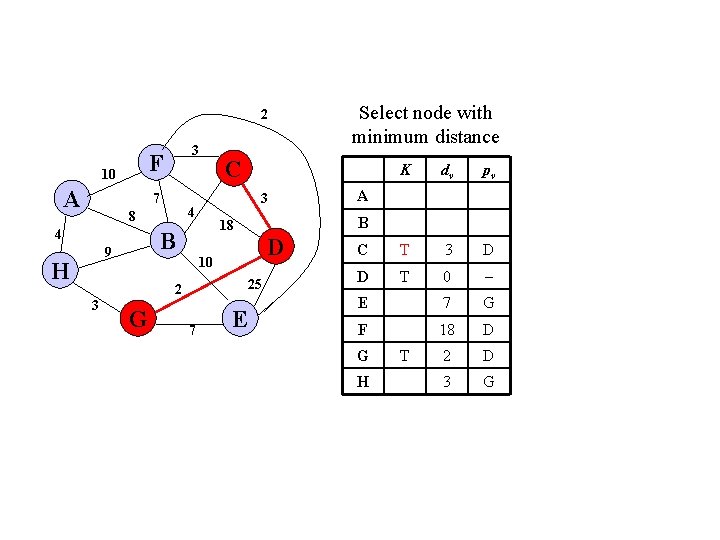
2 F 10 A 3 7 4 H G D 25 7 E dv pv 3 D 0 E 25 D F 18 D 2 D A B 10 2 3 K 18 B 9 C 3 4 8 Select node with minimum distance C D G H T T

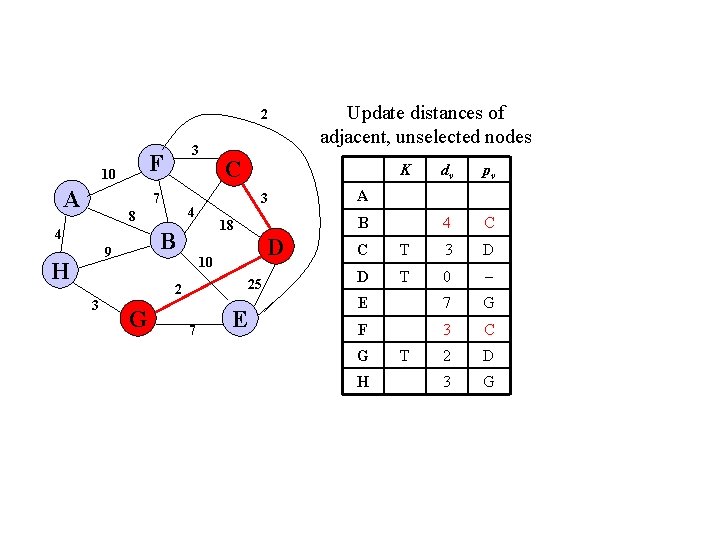
2 F 10 A 3 7 4 H G D 25 7 E dv pv 3 D 0 E 7 G F 18 D 2 D 3 G A B 10 2 3 K 18 B 9 C 3 4 8 Update distances of adjacent, unselected nodes C D G H T T

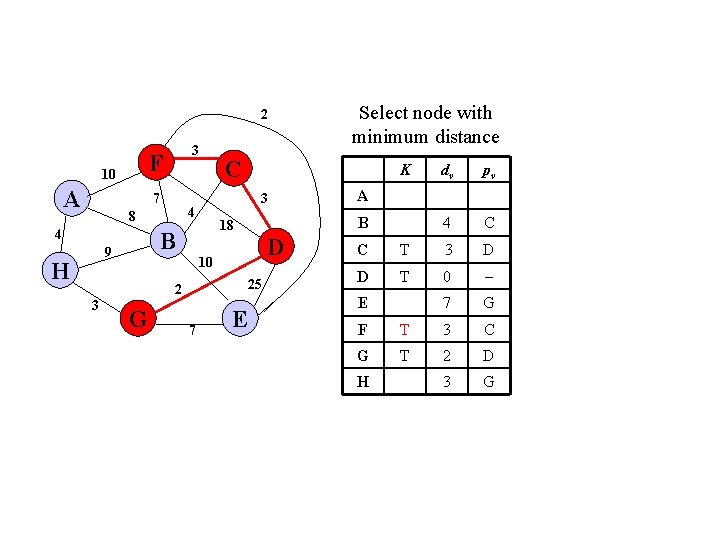
2 F 10 A 3 7 4 H 3 D 10 25 2 G 7 E K dv pv C T 3 D D T 0 E 7 G F 18 D 2 D 3 G A B 18 B 9 C 3 4 8 Select node with minimum distance G H T

2 F 10 A 3 7 4 H D 25 G 7 E dv pv 4 C A B 10 2 3 K 18 B 9 C 3 4 8 Update distances of adjacent, unselected nodes C T 3 D D T 0 E 7 G F 3 C 2 D 3 G G H T

2 F 10 A 3 7 4 H D 25 G 7 E dv pv 4 C A B 10 2 3 K 18 B 9 C 3 4 8 Select node with minimum distance C T 3 D D T 0 7 G E F T 3 C G T 2 D 3 G H

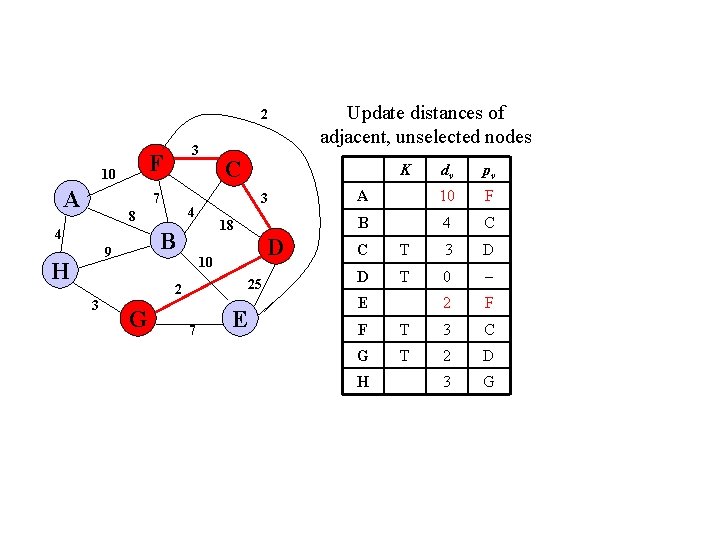
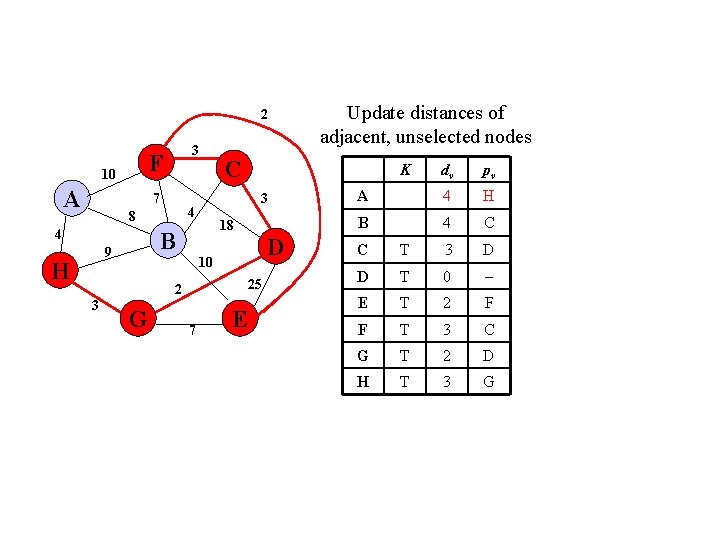
2 F 10 A 3 7 4 H D 10 25 2 3 K 18 B 9 C 3 4 8 G 7 Update distances of adjacent, unselected nodes E dv pv A 10 F B 4 C C T 3 D D T 0 2 F E F T 3 C G T 2 D 3 G H

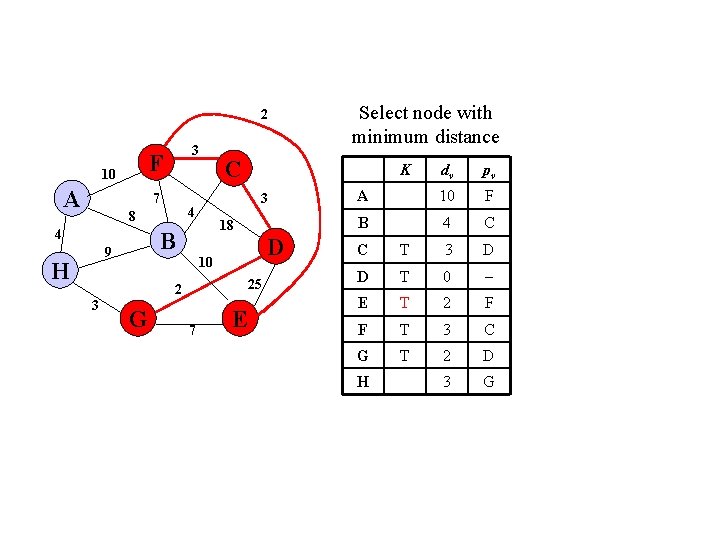
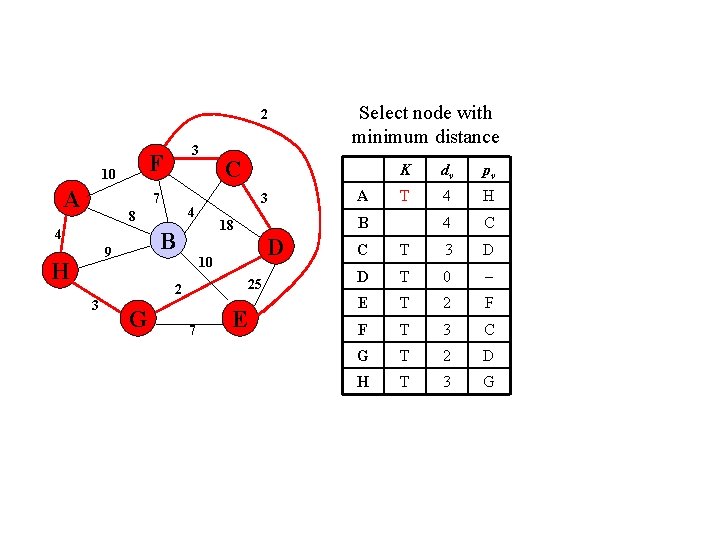
2 F 10 A 3 7 4 H D 10 25 2 3 K 18 B 9 C 3 4 8 G 7 Select node with minimum distance E dv pv A 10 F B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D 3 G H

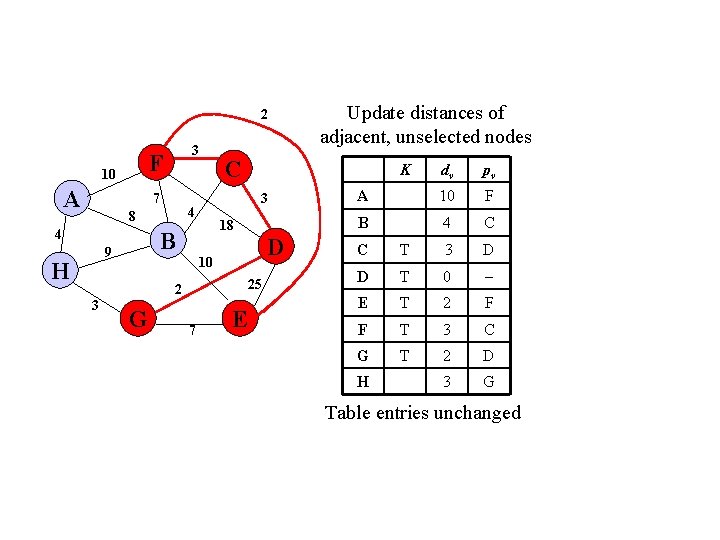
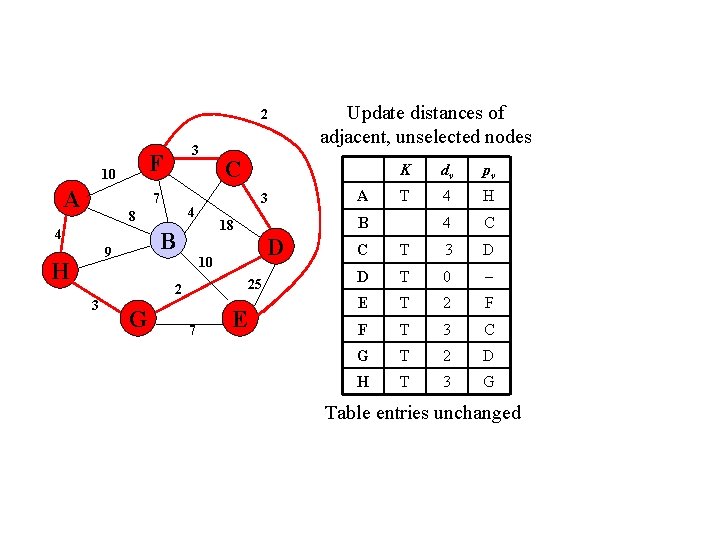
2 F 10 A 3 7 4 H D 10 25 2 3 K 18 B 9 C 3 4 8 G 7 Update distances of adjacent, unselected nodes E dv pv A 10 F B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D 3 G H Table entries unchanged

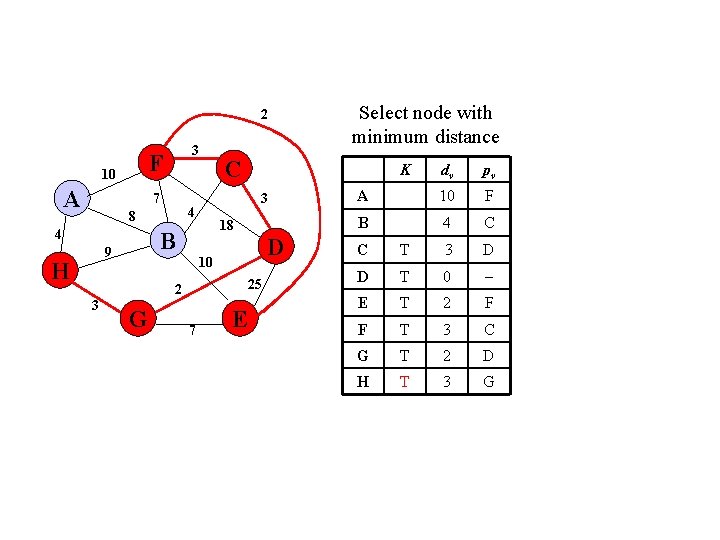
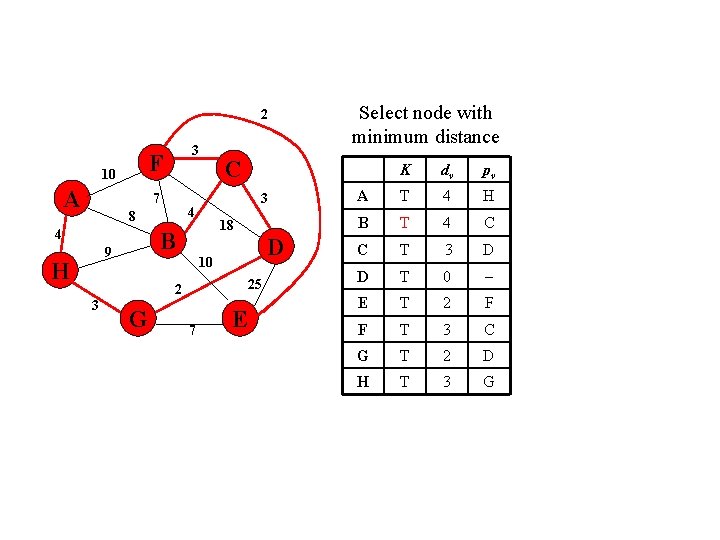
2 F 10 A 3 7 4 H D 10 25 2 3 K 18 B 9 C 3 4 8 G 7 Select node with minimum distance E dv pv A 10 F B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G

2 F 10 A 3 7 4 H D 10 25 2 3 K 18 B 9 C 3 4 8 G 7 Update distances of adjacent, unselected nodes E dv pv A 4 H B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G

2 F 10 A 3 7 4 H 3 D 10 25 2 G 7 E A K dv pv T 4 H 4 C B 18 B 9 C 3 4 8 Select node with minimum distance C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G

2 F 10 A 3 7 4 H 3 D 10 25 2 G 7 E A K dv pv T 4 H 4 C B 18 B 9 C 3 4 8 Update distances of adjacent, unselected nodes C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G Table entries unchanged

2 F 10 A 3 7 4 H 18 B 9 C 3 4 8 D 10 25 2 3 G 7 Select node with minimum distance E K dv pv A T 4 H B T 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G

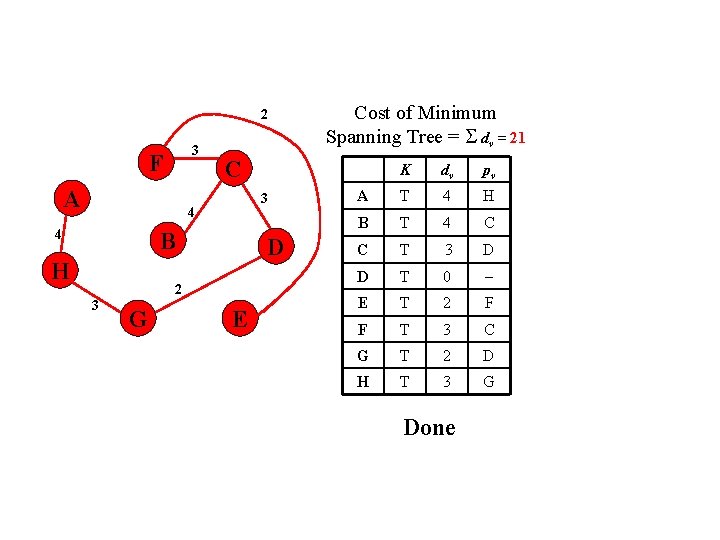
2 3 F A C 3 4 4 B H D 2 3 G Cost of Minimum Spanning Tree = dv = 21 E K dv pv A T 4 H B T 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G Done

Kruskal’s Algorithm • Work with edges, rather than nodes • Two steps: – Sort edges by increasing edge weight – Select the first |V| – 1 edges that do not generate a cycle

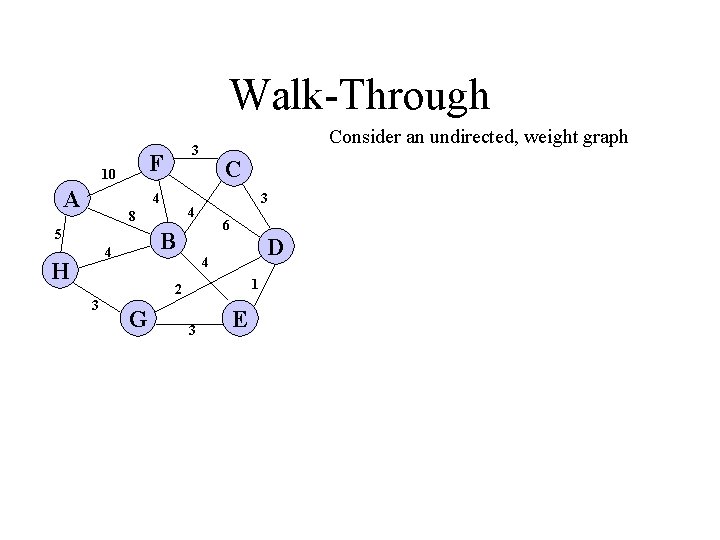
Walk-Through F 10 A 4 3 6 B 4 H C 4 8 5 Consider an undirected, weight graph 3 D 4 1 2 3 G 3 E

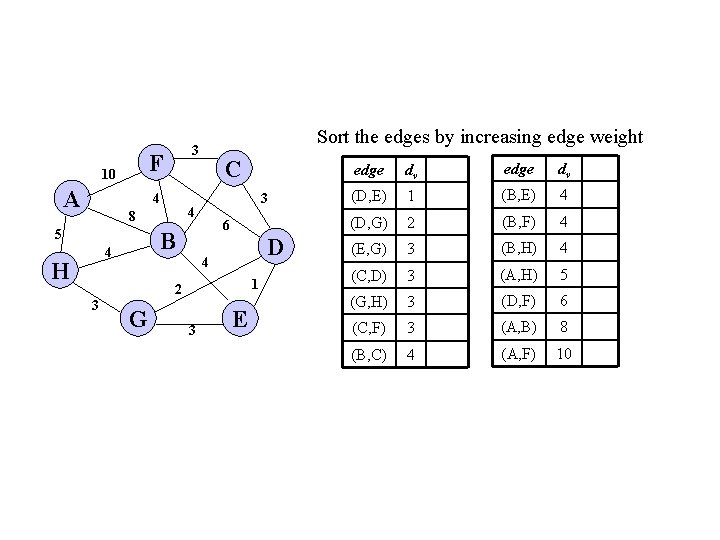
F 10 A 4 3 6 B 4 H C 4 8 5 Sort the edges by increasing edge weight 3 D 4 1 2 3 G 3 E edge dv (D, E) 1 (B, E) 4 (D, G) 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10

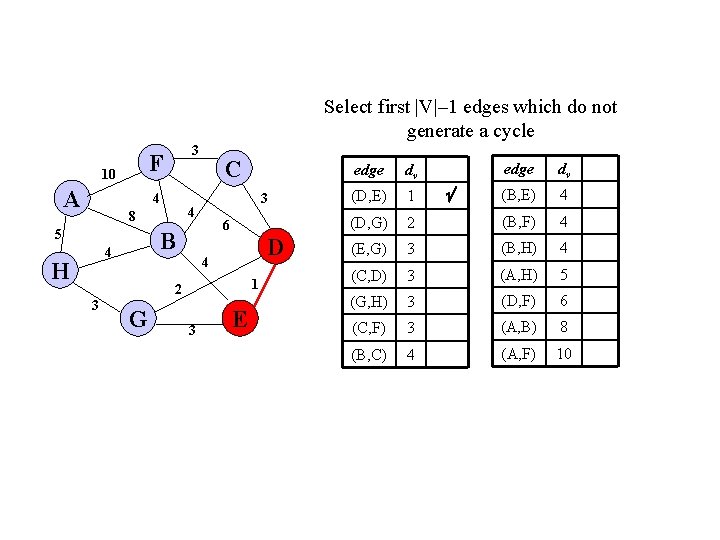
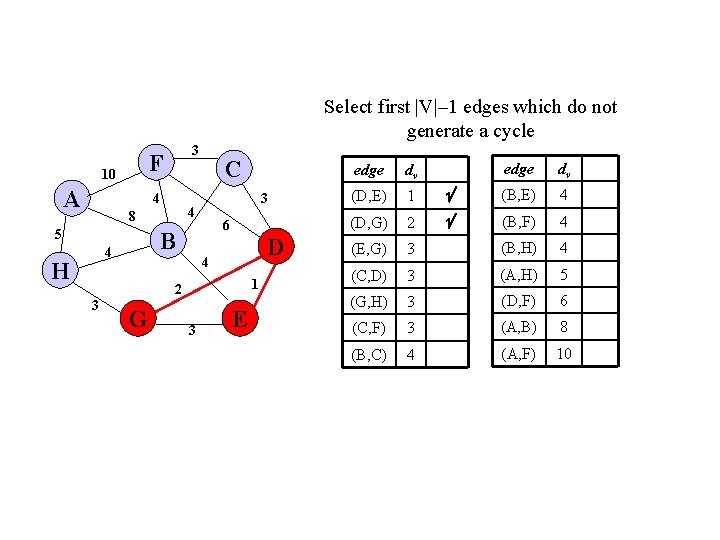
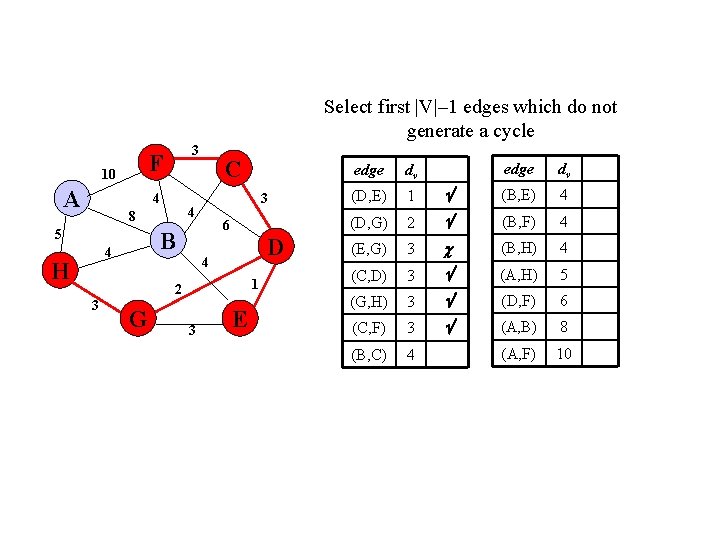
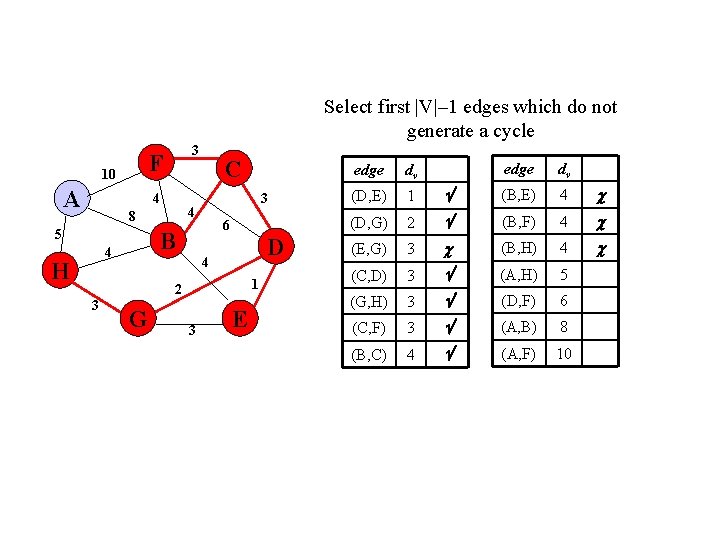
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G)

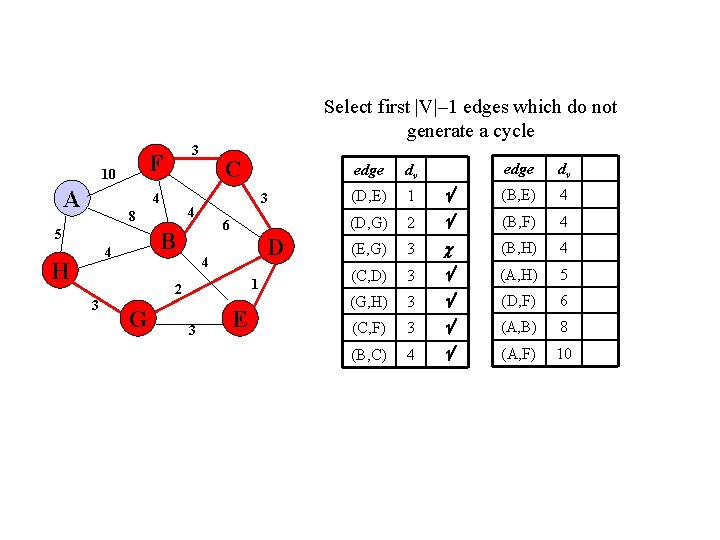
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 (B, F) 4 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G) 2 (E, G)

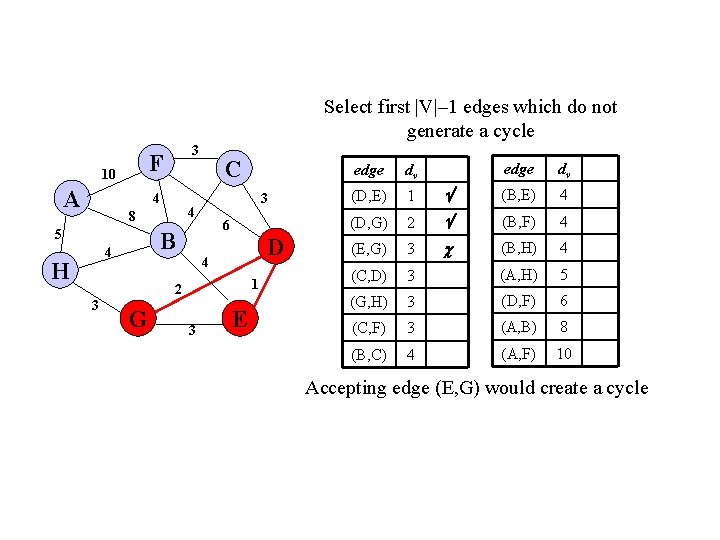
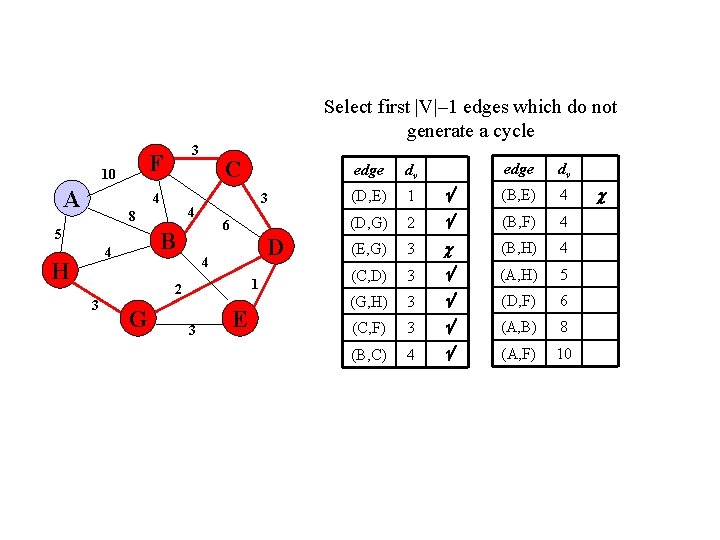
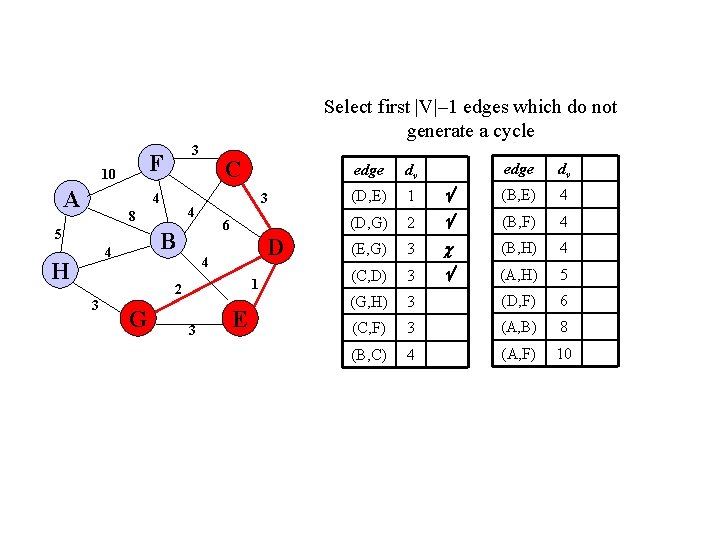
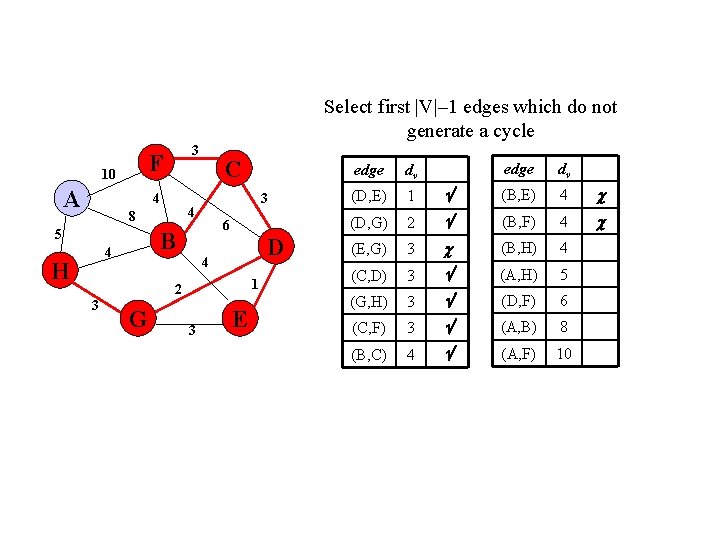
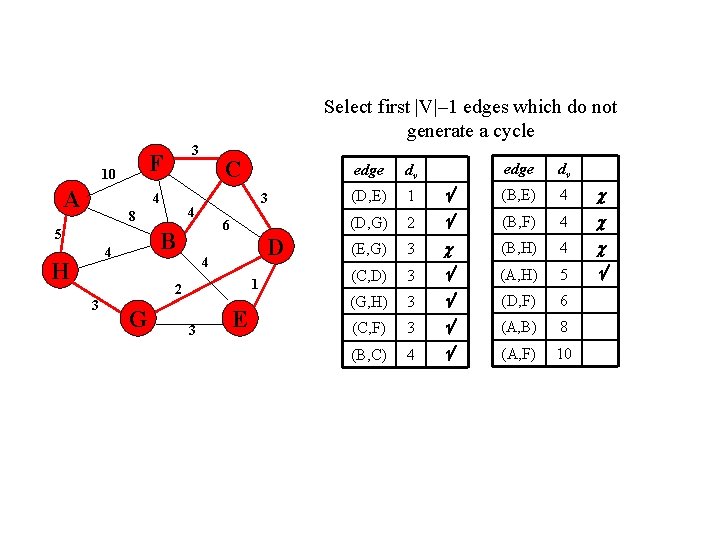
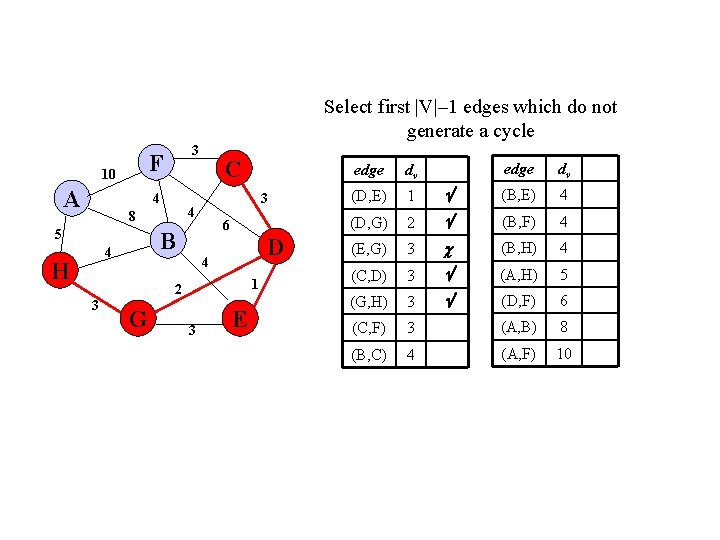
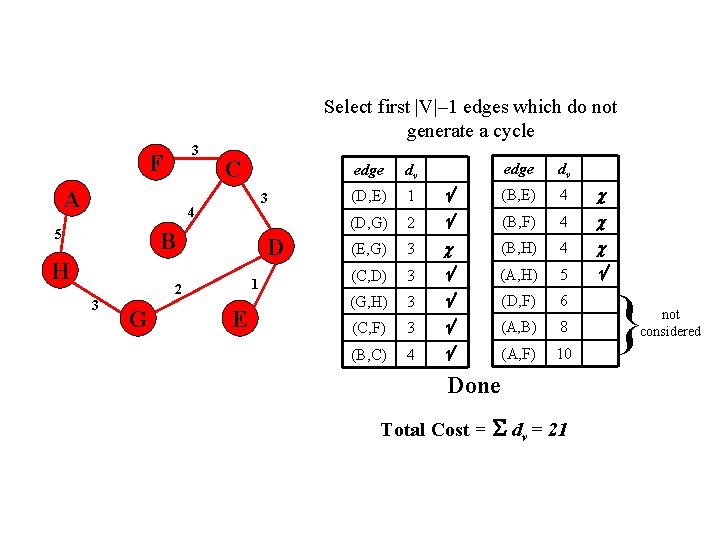
Select first |V|– 1 edges which do not generate a cycle 3 F A C 3 4 5 B H D 1 2 3 G E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G) Done Total Cost = dv = 21 } not considered

Detecting Cycles • Use Disjoint Sets (Chapter 8)