The Theory of NPCompleteness 1 Review Finding lower





















































- Slides: 60

The Theory of NP-Completeness 1

Review: Finding lower bound by problem transformation n Problem X reduces to problem Y (X Y) n n iff X can be solved by using any algorithm which solves Y. If X Y, Y is more difficult. If Y is solved, then X is solved, but not vice versa. So, Y is at least as hard as X. So, the lower bound L(X) of the problem X is also the lower bound L(Y) of the problem Y (i. e. , L(Y) L(X)). 2

The lower bound of the convex hull problem n n n By known one unknown one sorting convex hull X Y an instance of X: (x 1, x 2, …, xn) ↓transformation an instance of Y: {( x 1, x 12), ( x 2, x 22), …, ( xn, xn 2)} assume: x 1 < x 2 < …< xn 3

The lower bound of the convex hull problem n n n If the convex hull problem can be solved, we can also solve the sorting problem, but not vice versa. We have that the convex hull problem is harder than the sorting problem. The lower bound of sorting problem is (n log n), so the lower bound of the convex hull problem is also (n log n). 4

n n NP : the class of decision problem which can be solved by a non-deterministic polynomial algorithm. P: the class of problems which can be solved by a deterministic polynomial algorithm. NP-hard: the class of problems to which every NP problem reduces. (It is “at least as hard as the hardest problems in NP. ”) NP-complete: the class of problems which are NP -hard and belong to NP. 5

Nondeterministic algorithms n n A nondeterministic algorithm is an algorithm consisting of two phases: guessing (or choice) and checking. Furthermore, it is assumed that a nondeterministic algorithm always makes a correct guessing. 6

Nondeterministic algorithms n n Machines for running nondeterministic algorithms do not exist and they would never exist in reality. (They can only be made by allowing unbounded parallelism in computation. ) (Quantum computation may be an approximation. ) Nondeterministic algorithms are useful only because they will help us define a class of problems: NP problems 7

NP (Nondeterministic Polynomial) algorithm n If the checking stage of a nondeterministic algorithm is of polynomial timecomplexity, then this algorithm is called an NP (nondeterministic polynomial) algorithm. 8

NP problem (By Lee’s) n n If a decision problem can be solved by a NP algorithm, this problem is called an NP (nondeterministic polynomial) problem. NP problems : (must be decision problems) 9

Decision problems n n n The solution is simply “Yes” or “No”. Optimization problem : harder Decision problem : easier E. g. the traveling salesperson problem n n Optimization version: Find the shortest tour Decision version: Is there a tour whose total length is less than or equal to a constant C ? 10

Decision version of sorting n Given a 1, a 2, …, an and c, is there a permutation of ai s ( a 1 , a 2 , … , an ) such that∣a 2 –a 1 ∣+∣a 3 –a 2 ∣+ … +∣an – an-1 ∣< C ? 11

Decision vs Original Version n We consider decision version problem D rather than the original problem O n because we are addressing the lower bound of a problem n and D ∝ O 12

To express Nondeterministic Algorithm by three special commands Choice(S) : arbitrarily chooses one of the elements in set S at one step n Failure : an unsuccessful completion n Success : a successful completion n 13

Example: Nondeterministic searching Algorithm input: n elements and a target element x output: success if x is found among the n elements; failure, otherwise. j ← choice(1 : n) /* guess if A(j) = x then success /* check else failure n A nondeterministic algorithm terminates unsuccessfully n iff there exist no set of choices leading to a success signal. The time required for choice(1 : n) is O(1). 14

Relationship Between NP and P It is known P NP. However, it is not known whether P=NP or whether P is a proper subset of NP It is believed NP is much larger than P n n n n We cannot find a polynomial-time algorithm for many NP problems. But, no NP problem is proved to have exponential lower bound. (No NP problem has been proved to be not in P. ) So, “does P = NP? ” is still an open question! Cook tried to answer the question by proposing NPC. 15

NP-hard n A problem X is NP-hard if every NP problem (polynomially) reduces to X. 16

NP-complete (NPC) A problem X is NP-complete (NPC) if X∈NP and every NP problem (polynomially) reduces to X. n So, X NPC if X NP-hard and X NP n 17

Cook’s Theorem (1971) n n n Prof. Cook Toronto U. Receiving Turing Award (1982) Discussing difficult problems whose worst case lower bound seems to be in the order of an exponential function The problems are called NP-complete (NPC) Problems 18

Cook’s Theorem (1971) NP = P iff SAT P n That is, NP = P iff the satisfiability (SAT) problem is a P problem n SAT is NP-complete n It is the first NP-complete problem n Every NP problem reduces to SAT n 19

SAT is NP-complete n n n Every NP problem can be solved by an NP algorithm Every NP algorithm can be transformed in polynomial time to an SAT problem Such that the SAT problem is satisfiable iff the answer for the original NP problem is “yes” That is, every NP problem SAT is NP-complete 20

Proof of NP-Completeness n n n To show that X is NP-complete (I) Prove that X is an NP problem (II) Prove that Y NPC, Y X X NPC Why ? Transitive property of polynomial-time reduction 21

Karp R. Karp showed several NPC problems, such as 3 -STA, node (vertex) cover, and Hamiltonian cycle problems, etc. n Karp received Turing Award in 1985 n 22

NP-Completeness Proof: Reduction All NP problems SAT Clique Vertex Cover 3 -SAT Chromatic Number Dominating Set 23

NP-Completeness “NP-complete problems”: the hardest problems in NP Interesting property n n If any one NP-complete problem can be solved in polynomial time, then every problem in NP can also be solved in polynomial time (i. e. , P=NP) Many believe P≠NP 24

Importance of NP-Completeness n n n NP-complete problems: considered “intractable” Important for algorithm designers & engineers Suppose you have a problem to solve n n Your colleagues have spent a lot of time to solve it exactly but in vain See whether you can prove that it is NP-complete If yes, then spend your time developing an approximation (heuristic) algorithm Many natural problems can be NP-complete 25

Some concepts n n Up to now, none of the NPC problems can be solved by a deterministic polynomial time algorithm in the worst case. It does not seem to have any polynomial time algorithm to solve the NPC problems. The lower bound of any NPC problem seems to be in the order of an exponential function. The theory of NP-completeness always considers the worst case. 26

Caution ! If a problem is NP-complete, its special cases may or may not be of exponential timecomplexity. n We consider worst case lower bound in NP-complete. n 27

Even harder problems: Undecidable Problems They cannot be solved by guessing and checking. n They are even more difficult than NP problems. n E. G. : Halting problem: Given an arbitrary program with an arbitrary input data (the number of input cases is infinite), will the program terminate or not? n It is not NP n It is NP-hard (SAT Halting problem) n 28

Some known NPC problems n n n n n SAT problem 3 SAT problem 0/1 knapsack problem Traveling salesperson problem Partition problem Art gallery problem Clique problem Vertex Cover problem Dominating Set problem Chromatic Coloring problem 29

The satisfiability (SAT) problem n Def : Given a Boolean formula, determine whether this formula is satisfiable or not. n n n A literal (Boolean variable): xi or -xi A clause (disjunction of variables): ci x 1 v x 2 v -x 3 A formula : conjunctive normal form C 1& c 2 & … & c m 30

NPC Problems • • SAT: Give a Boolean expression (formula) in CNF (conjunctive normal form), determine if it is satisfiable. 3 SAT: Give a Boolean expression in CNF such that each clause has exactly 3 variables (literals), determine if it is satisfiable. 31

The satisfiability (SAT) problem n The satisfiability problem n The logical formula : x 1 v x 2 v x 3 & - x 1 & - x 2 the assignment : x 1 ← F , x 2 ← F , x 3 ← T will make the above formula true (-x 1, -x 2 , x 3) represents x 1 ← F , x 2 ← F , x 3 ← T 32

The satisfiability problem n n If there is at least one assignment which satisfies a formula, then we say that this formula is satisfiable; satisfiable otherwise, it is unsatisfiable An unsatisfiable formula : x 1 v x 2 & x 1 v -x 2 & -x 1 v -x 2 33

Resolution principle Let formula F= c 1 : -x 1 v -x 2 v x 3 c 2 : x 1 v x 4 c 3 : -x 2 v x 3 v x 4 (resolvent) x 1 cannot satisfy c 1 and c 2 at the same time, so it is deleted to deduce a resolvent of c 1 and c 2. This is called the resolution principle. 34

Satisfiable n If no new clauses can be deduced satisfiable -x 1 v -x 2 v x 3 x 1 x 2 (1) & (2) -x 2 v x 3 (4) & (3) x 3 (1) & (3) -x 1 v x 3 (1) (2) (3) (4) (5) (6) 35

Unsatisfiable If an empty clause is deduced unsatisfiable n - x 1 v -x 2 v x 3 x 1 v -x 2 - x 3 deduce (1) & (2) -x 2 v x 3 (4) & (5) -x 2 (6) & (3) □ (1) (2) (3) (4) (5) (6) (7) 36

Nondeterministic SAT n Guessing Checking for i = 1 to n do xi ← choice( true, false ) if E(x 1, x 2, … , xn) is true then success else failure 37

Proof of Cook’s Theory n n Dr. Cook Prove theory by showing that all instance of NP algorithm can reduce to SAT problem. Below, we show a simple example that the NP searching algorithm reduces to the SAT problem. 38

The NP searching algorithm reduces to the SAT problem n n n Does there exist a number in { x(1), x(2), …, x(n) }, which is equal to 7? Assume n = 2 The algorithm: 39

The NP searching algorithm reduces to SAT i=1 v i=2 & i=1 → i≠ 2 & i=2 → i≠ 1 & x(1)=7 & i=1 → SUCCESS & x(2)=7 & i=2 → SUCCESS & x(1)≠ 7 & i=1 → FAILURE & x(2)≠ 7 & i=2 → FAILURE & FAILURE → -SUCCESS & SUCCESS (Guarantees a successful termination) & x(1)=7 (Input Data) & x(2)≠ 7 40

The NP searching algorithm reduces to SAT n CNF (conjunctive normal form) : i=1 v i=2 i≠ 1 v i≠ 2 x(1)≠ 7 v i≠ 1 v SUCCESS x(2)≠ 7 v i≠ 2 v SUCCESS x(1)=7 v i≠ 1 v FAILURE x(2)=7 v i≠ 2 v FAILURE -FAILURE v -SUCCESS x(1)=7 x(2)≠ 7 (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) 41

The NP searching algorithm reduces to SAT n Satisfiable at the following assignment : i=1 i≠ 2 SUCCESS -FAILURE x(1)=7 x(2)≠ 7 satisfying satisfying (1) (2), (4) and (6) (3), (4) and (8) (7) (5) and (9) (4) and (10) 42

The NP searching algorithm reduces to SAT n Searching for 7, but x(1) 7, x(2) 7 CNF : 43

The NP searching algorithm reduces to SAT n Apply resolution principle : 44

Searching in CNF with inputs n 45

0/1 Knapsack problem Profit P 1 P 2 P 3 P 4 P 5 P 6 P 7 P 8 10 5 1 9 3 4 11 17 3 3 10 1 9 22 15 Weight 7 n Given M (weight limit) and P, is there is a solution with a profit larger than P? This is an NPC problem. 46

Traveling salesperson problem n n Given: A set of n planar points and a value L Find: Is there a closed tour which includes all points exactly once such that its total length is less than L? This is an NPC problem. 47

Partition problem n n Given: A set of positive integers S Find: Is there a partition of S 1 and S 2 such that S 1 S 2= , S 1 S 2=S, i S 1 i= i S 2 i (partition S into S 1 and S 2 such that element sum of S 1 is equal to that of S 2) e. g. S={1, 7, 10, 9, 5, 8, 3, 13} n n n S 1={1, 10, 9, 8} S 2={7, 5, 3, 13} This problem is NP-complete. 48

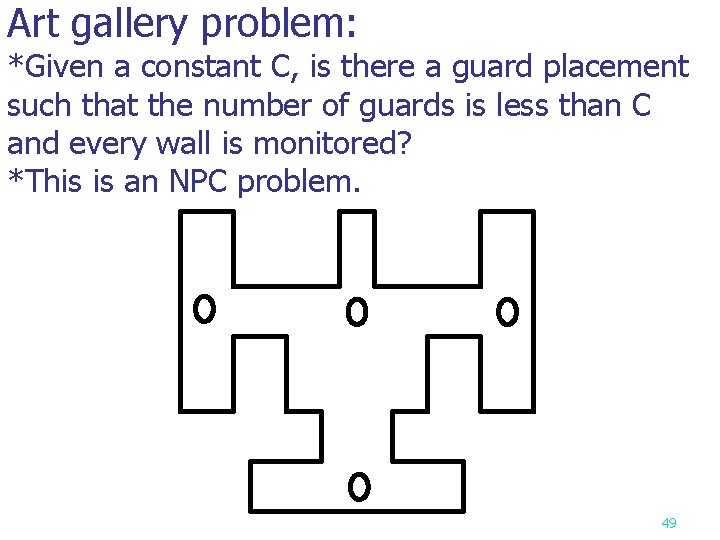
Art gallery problem: *Given a constant C, is there a guard placement such that the number of guards is less than C and every wall is monitored? *This is an NPC problem. 49

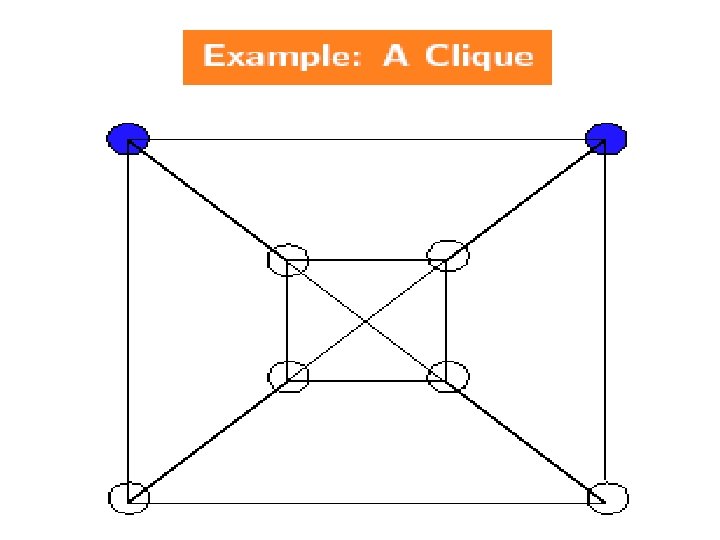
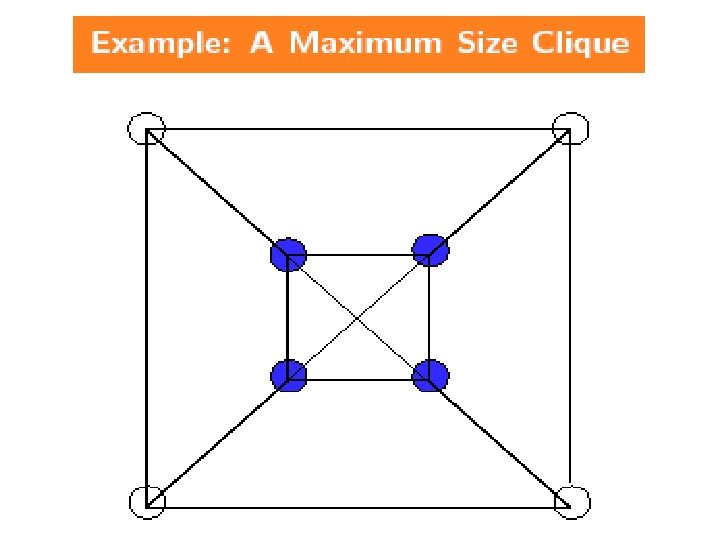
NPC Problems n CLIQUE(k): Does G=(V, E) contain a clique of size k? Definition: q A clique in a graph is a set of vertices such that any pair of vertices are joined by en edge. 50



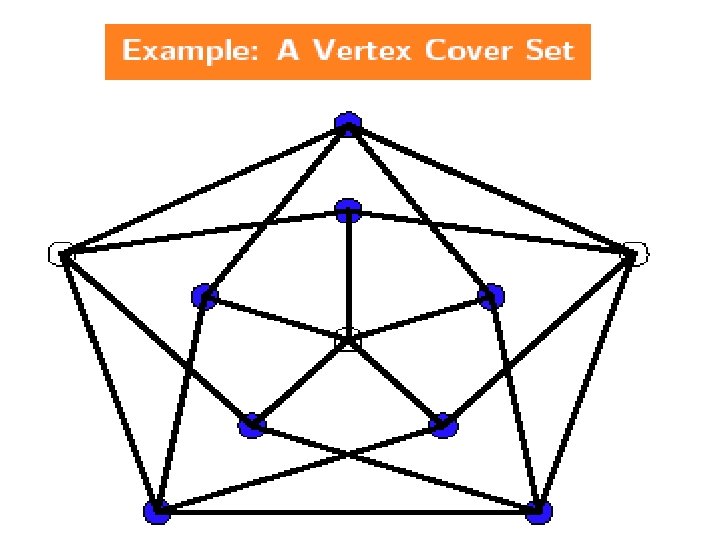
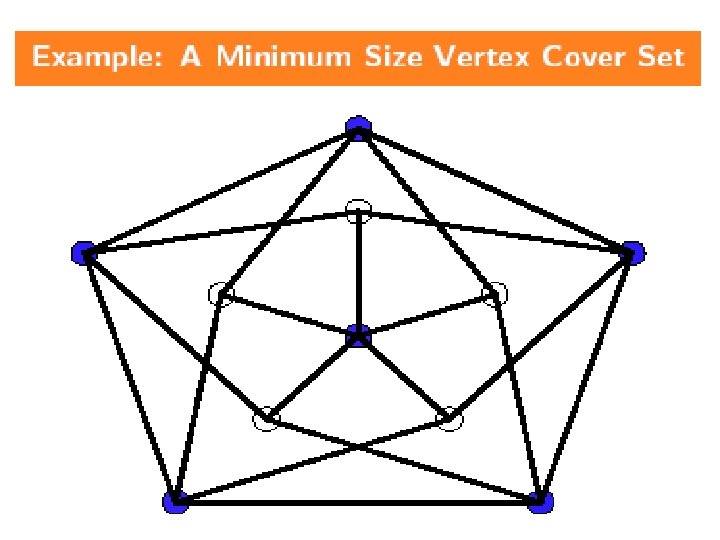
NPC Problems n Vertex Cover(k): Given a graph G=(V, E) and an integer k, does G have a vertex cover with k vertices? Definition: n A vertex cover of G=(V, E) is V’ V such that every edge in E is incident to some v V’. 53



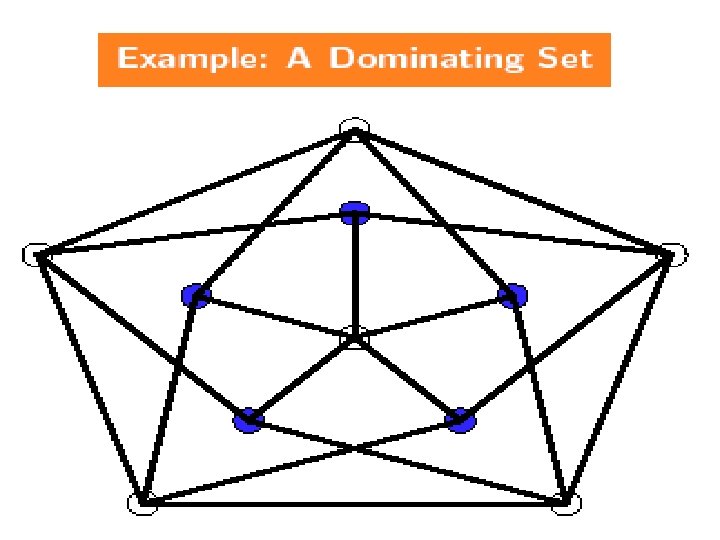
NPC Problems Dominating Set(k): Given an graph G=(V, E) and an integer k, does G have a dominating set of size k ? Definition: q A dominating set D of G=(V, E) is D V such that every v V is either in D or adjacent to at least one vertex of D. n 56



NPC Problems Chromatic Coloring(k): Given a graph G=(V, E) and an integer k, does G have a coloring for k Definition • n A coloring of a graph G=(V, E) is a function f : V { 1, 2, 3, …, k } if (u, v) E, then f(u) f(v). 59

Q&A 60