CS 2133 Algorithms Topological Sort Minimum Spanning Tree

CS 2133: Algorithms Topological Sort Minimum Spanning Tree

Review: Breadth-First Search BFS(G, s) { initialize vertices; Q = {s}; // Q is a queue (duh); initialize to s while (Q not empty) { u = Remove. Top(Q); for each v u->adj { if (v->color == WHITE) v->color = GREY; v->d = u->d + 1; v->d represents depth in tree v->p = u; v->p represents parent in tree Enqueue(Q, v); } u->color = BLACK; } }

Review: Depth-First Search l Depth-first search is another strategy for exploring a graph n n n Explore “deeper” in the graph whenever possible Edges are explored out of the most recently discovered vertex v that still has unexplored edges When all of v’s edges have been explored, backtrack to the vertex from which v was discovered

Review: DFS Code DFS(G) { for each vertex u G->V { u->color = WHITE; } time = 0; for each vertex u G->V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; }

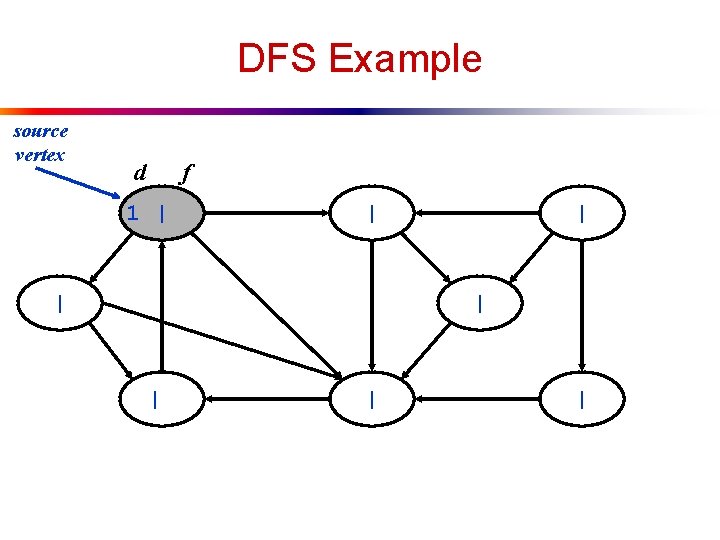
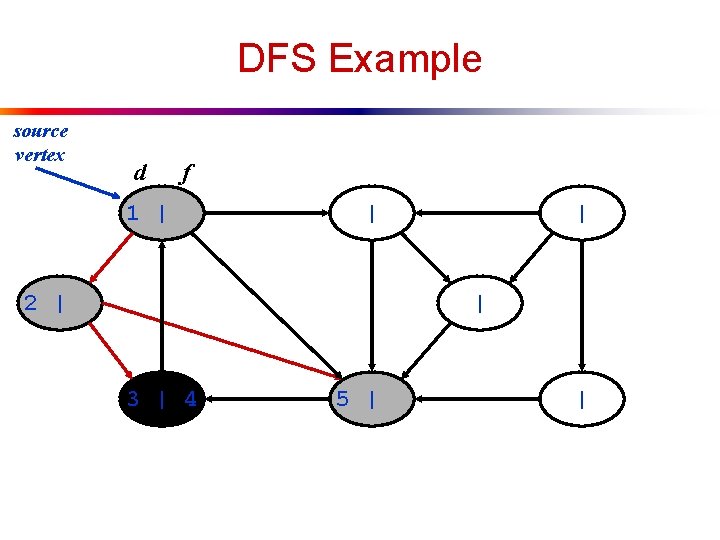
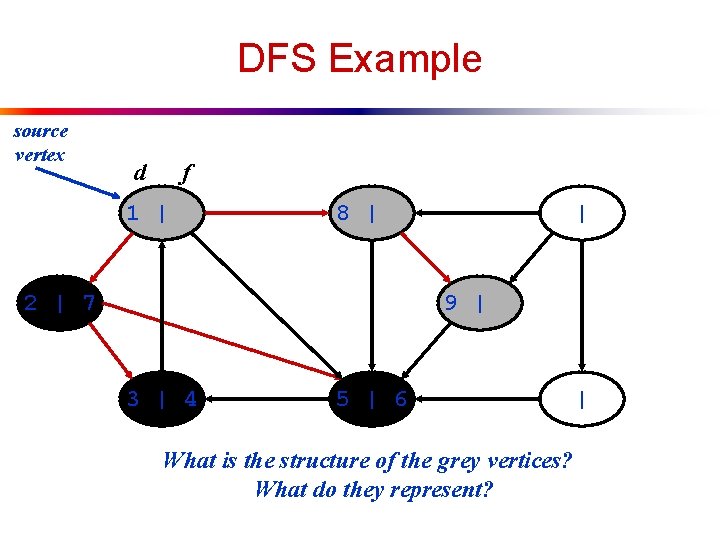
DFS Example source vertex d f 1 | | | |

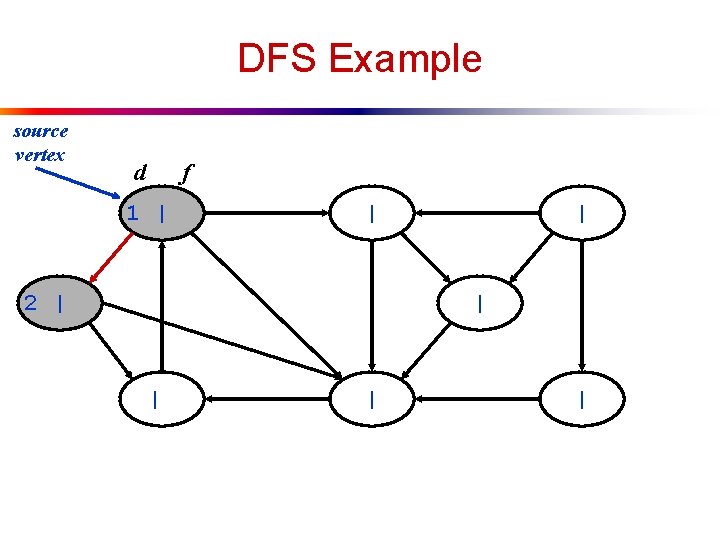
DFS Example source vertex d f 1 | | 2 | | |

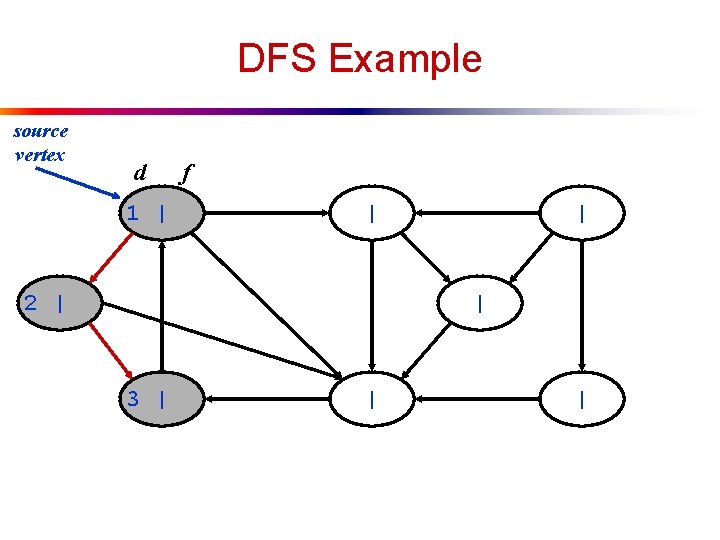
DFS Example source vertex d 1 | f | 2 | | | 3 | | |

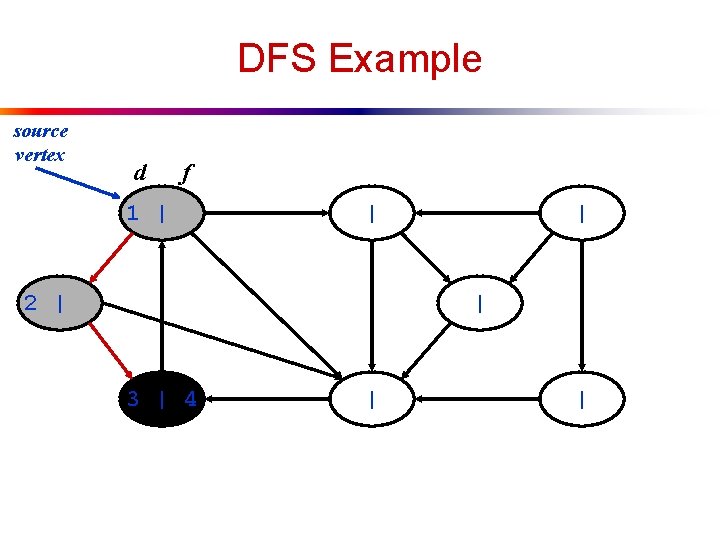
DFS Example source vertex d f 1 | | 2 | | | 3 | 4 | |

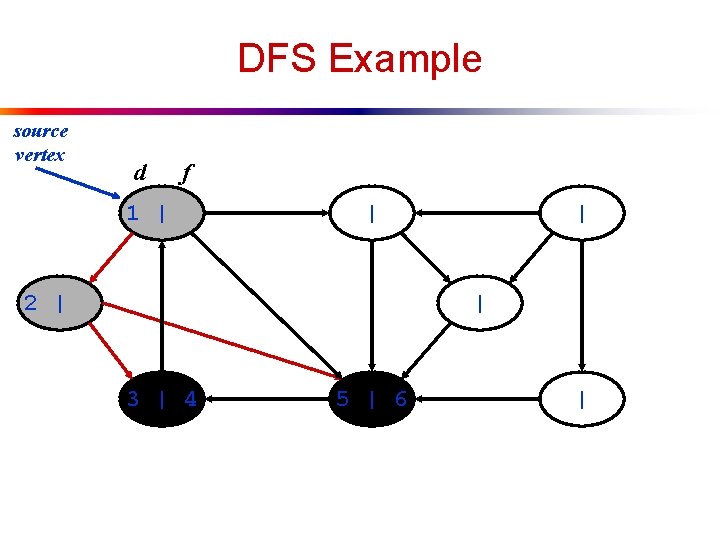
DFS Example source vertex d f 1 | | 2 | | | 3 | 4 5 | |

DFS Example source vertex d f 1 | | 2 | | | 3 | 4 5 | 6 |

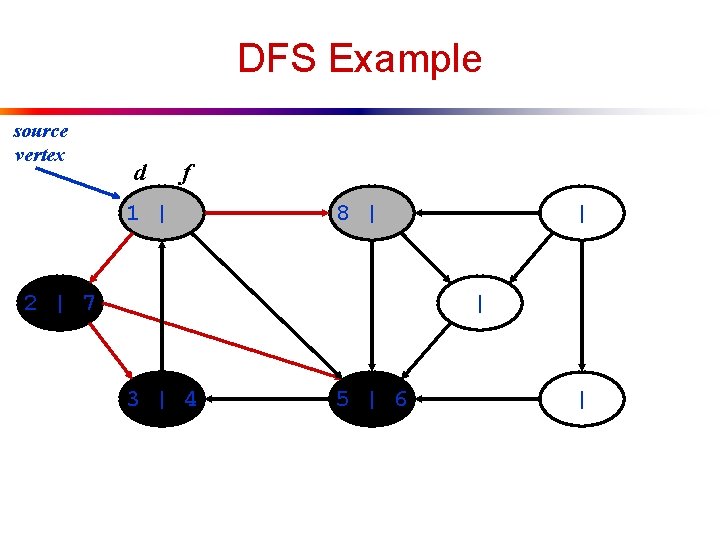
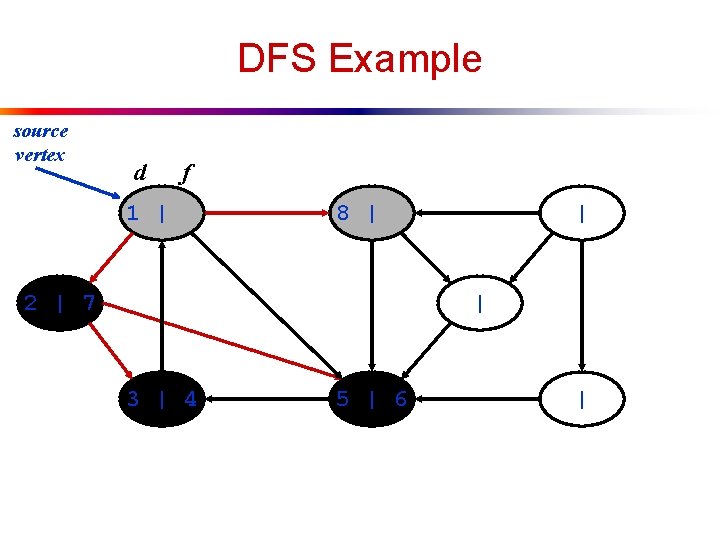
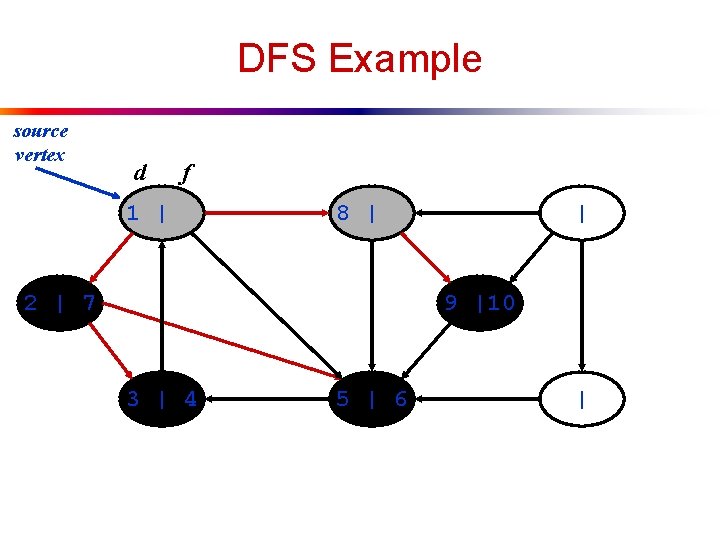
DFS Example source vertex d f 1 | 8 | 2 | 7 | | 3 | 4 5 | 6 |

DFS Example source vertex d f 1 | 8 | 2 | 7 | | 3 | 4 5 | 6 |

DFS Example source vertex d f 1 | 8 | 2 | 7 | 9 | 3 | 4 5 | 6 What is the structure of the grey vertices? What do they represent? |

DFS Example source vertex d f 1 | 8 | 2 | 7 | 9 |10 3 | 4 5 | 6 |

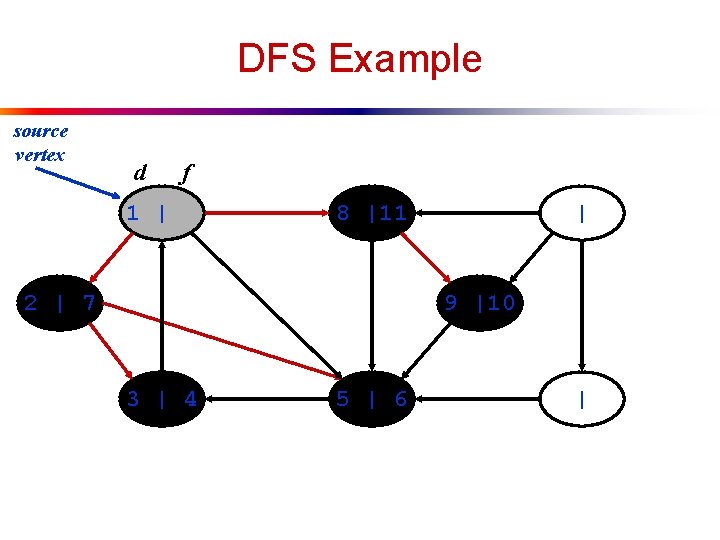
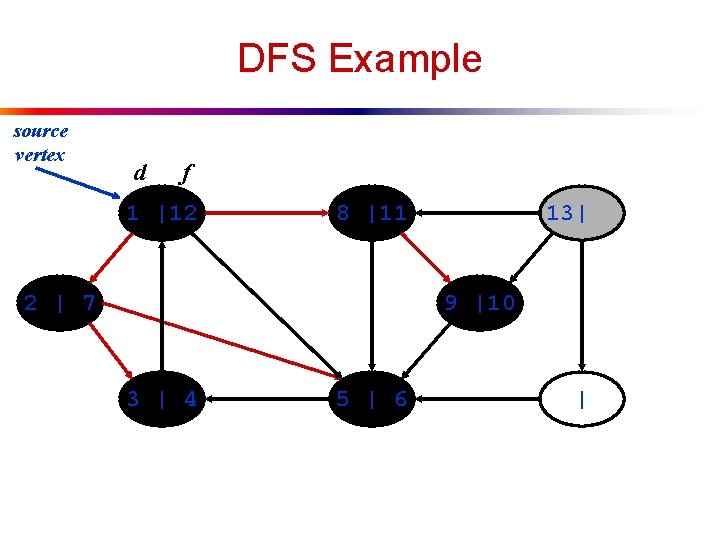
DFS Example source vertex d f 1 | 8 |11 2 | 7 | 9 |10 3 | 4 5 | 6 |

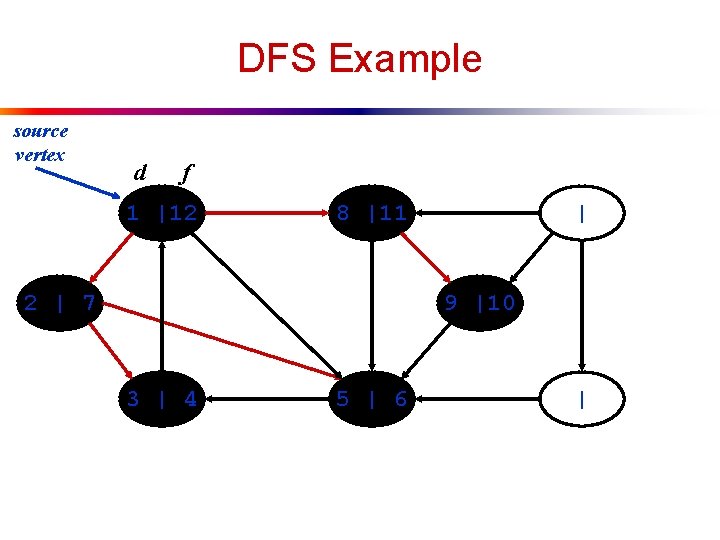
DFS Example source vertex d f 1 |12 8 |11 2 | 7 | 9 |10 3 | 4 5 | 6 |

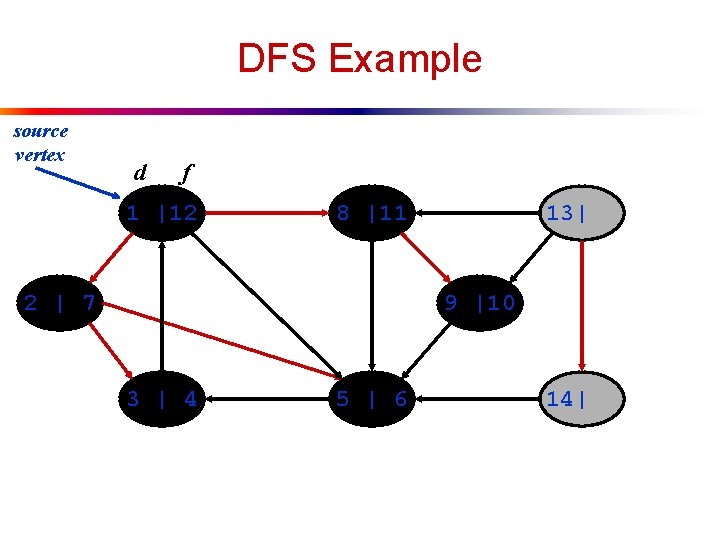
DFS Example source vertex d f 1 |12 8 |11 2 | 7 13| 9 |10 3 | 4 5 | 6 |

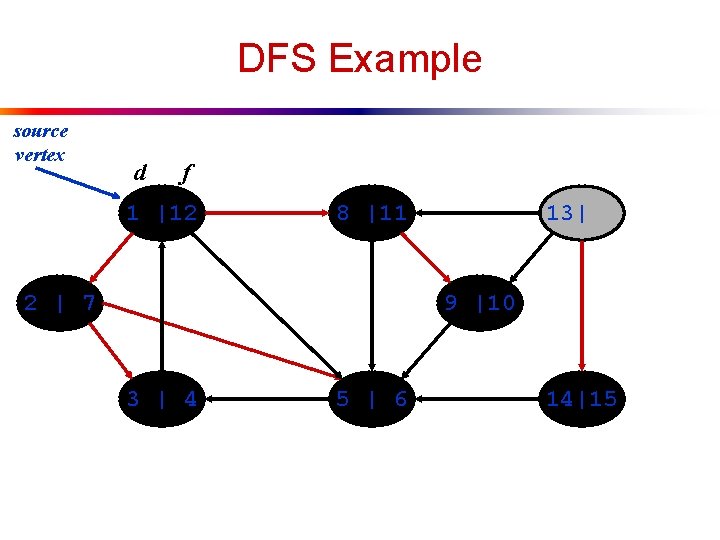
DFS Example source vertex d f 1 |12 8 |11 2 | 7 13| 9 |10 3 | 4 5 | 6 14|

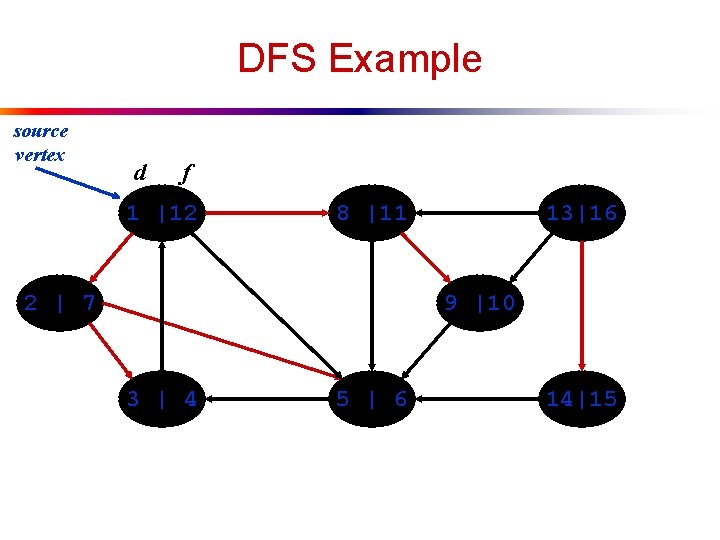
DFS Example source vertex d f 1 |12 8 |11 2 | 7 13| 9 |10 3 | 4 5 | 6 14|15

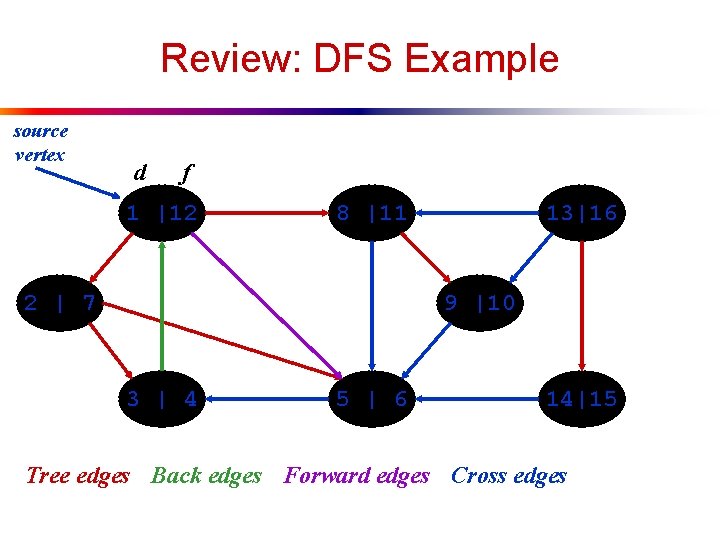
DFS Example source vertex d f 1 |12 8 |11 2 | 7 13|16 9 |10 3 | 4 5 | 6 14|15

Review: Depth-First Sort Analysis Running time: O(V+E) l Show by amortized analysis l n “Charge” the exploration of edge to the edge: u Each loop in DFS_Visit can be attributed to an edge in the graph u Runs once/edge if directed graph, twice if undirected u Thus loop will run in O(E) time, algorithm O(V+E) ] n Considered linear for graph, b/c adj list requires O(V+E) storage Important to be comfortable with this kind of reasoning and analysis

Review: Kinds of edges l DFS introduces an important distinction among edges in the original graph: n Tree edge: encounter new (white) vertex u The tree edges form a spanning forest u Can tree edges form cycles? Why or why not?

Review: Kinds of edges l DFS introduces an important distinction among edges in the original graph: n n Tree edge: encounter new (white) vertex Back edge: from descendent to ancestor u Encounter a grey vertex (grey to grey)

Review: Kinds of edges l DFS introduces an important distinction among edges in the original graph: n n n Tree edge: encounter new (white) vertex Back edge: from descendent to ancestor Forward edge: from ancestor to descendent u Not a tree edge, though u From grey node to black node

Review: Kinds of edges l DFS introduces an important distinction among edges in the original graph: n n Tree edge: encounter new (white) vertex Back edge: from descendent to ancestor Forward edge: from ancestor to descendent Cross edge: between a tree or subtrees u From a grey node to a black node

Review: DFS Example source vertex d f 1 |12 8 |11 2 | 7 13|16 9 |10 3 | 4 5 | 6 14|15 Tree edges Back edges Forward edges Cross edges

Review: Kinds Of Edges Thm: If G is undirected, a DFS produces only tree and back edges l Thm: An undirected graph is acyclic iff a DFS yields no back edges l n n If acyclic, no back edges If no back edges, acyclic u No back edges implies only tree edges (Why? ) u Only tree edges implies we have a tree or a forest u Which by definition is acyclic l Thus, can run DFS to find cycles

DFS And Cycles Running time: O(V+E) l We can actually determine if cycles exist in O(V) time: l n n n In an undirected acyclic forest, |E| |V| - 1 So count the edges: if ever see |V| distinct edges, must have seen a back edge along the way Why not just test if |E| <|V| and answer the question in constant time?

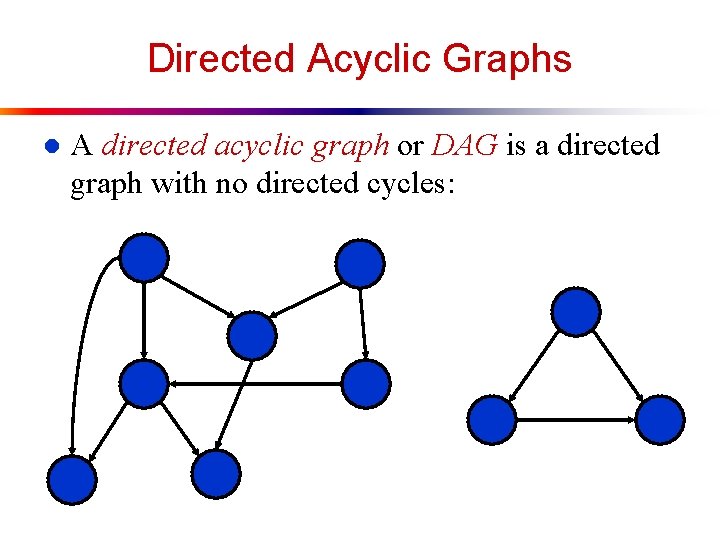
Directed Acyclic Graphs l A directed acyclic graph or DAG is a directed graph with no directed cycles:

DFS and DAGs l Argue that a directed graph G is acyclic iff a DFS of G yields no back edges: n Forward: if G is acyclic, will be no back edges u Trivial: n a back edge implies a cycle Backward: if no back edges, G is acyclic u Argue contrapositive: G has a cycle a back edge Let v be the vertex on the cycle first discovered, and u be the predecessor of v on the cycle ] When v discovered, whole cycle is white ] Must visit everything reachable from v before returning from DFS-Visit() ] So path from u v is grey, thus (u, v) is a back edge ]

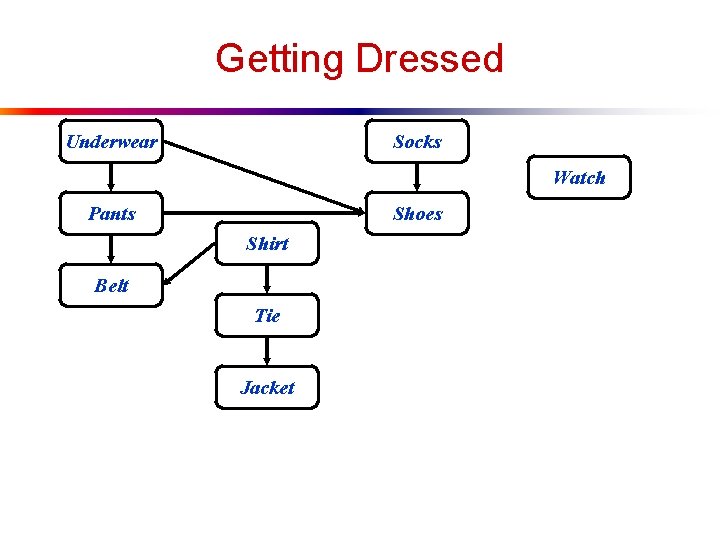
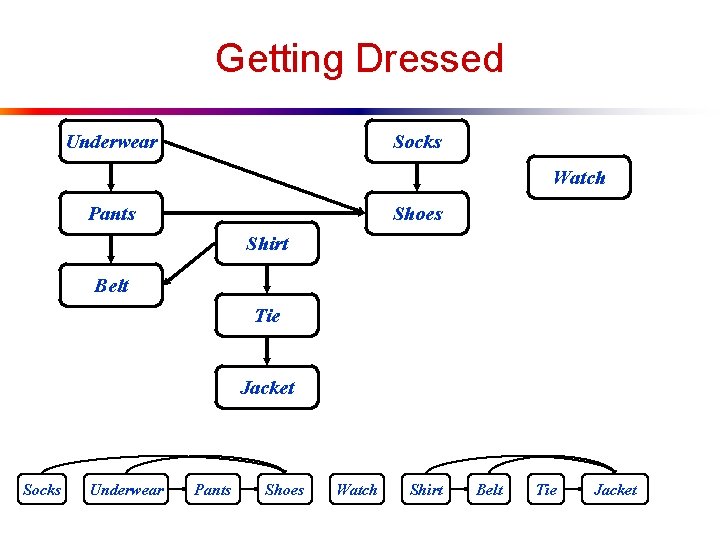
Topological Sort l Topological sort of a DAG: n l Linear ordering of all vertices in graph G such that vertex u comes before vertex v if edge (u, v) G Real-world example: getting dressed

Getting Dressed Underwear Socks Watch Pants Shoes Shirt Belt Tie Jacket

Getting Dressed Underwear Socks Watch Pants Shoes Shirt Belt Tie Jacket Socks Underwear Pants Shoes Watch Shirt Belt Tie Jacket

Topological Sort Algorithm Topological-Sort() { Run DFS When a vertex is finished, output it Vertices are output in reverse topological order } Time: O(V+E) l Correctness: Want to prove that (u, v) G u f > v f l

Correctness of Topological Sort l Claim: (u, v) G u f > v f n When (u, v) is explored, u is grey = grey (u, v) is back edge. Contradiction (Why? ) u v = white v becomes descendent of u v f < u f (since must finish v before backtracking and finishing u) u v = black v already finished v f < u f uv

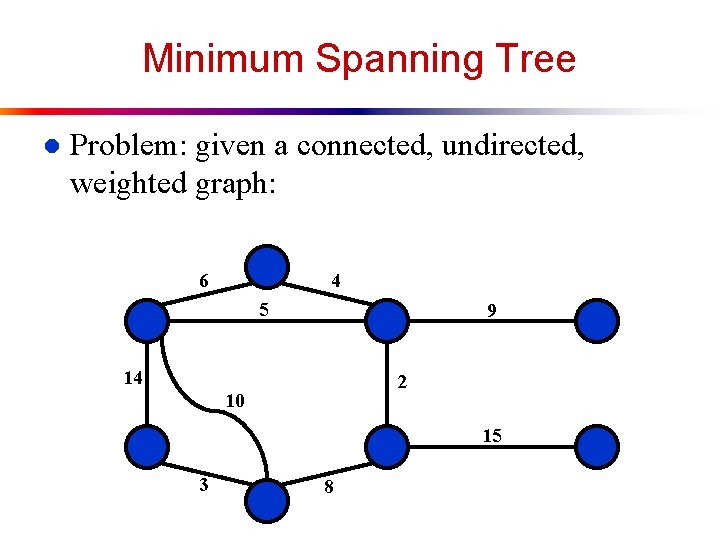
Minimum Spanning Tree l Problem: given a connected, undirected, weighted graph: 6 4 5 9 14 2 10 15 3 8

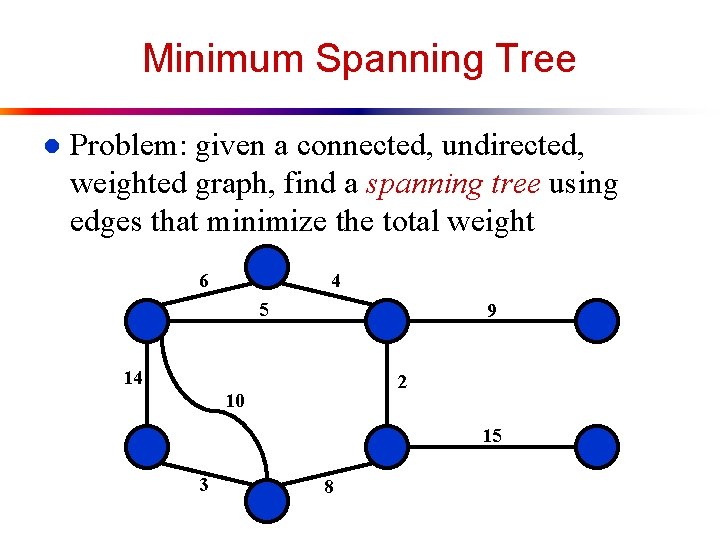
Minimum Spanning Tree l Problem: given a connected, undirected, weighted graph, find a spanning tree using edges that minimize the total weight 6 4 5 9 14 2 10 15 3 8

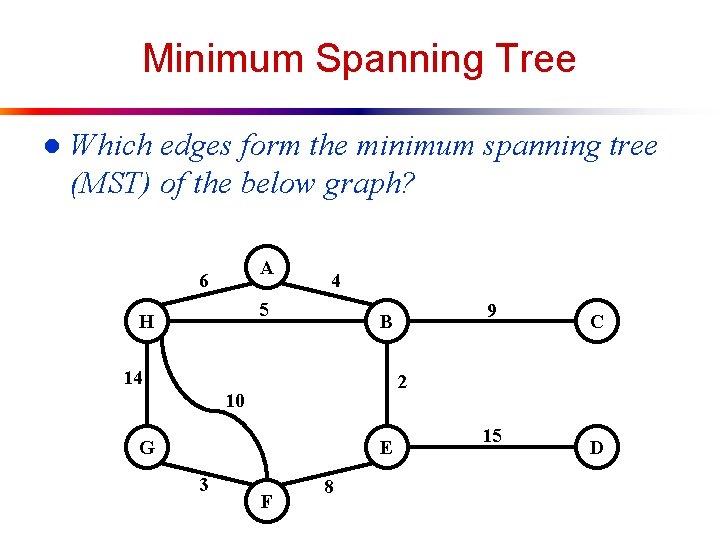
Minimum Spanning Tree l Which edges form the minimum spanning tree (MST) of the below graph? A 6 4 5 H 14 C 2 10 G E 3 9 B F 8 15 D

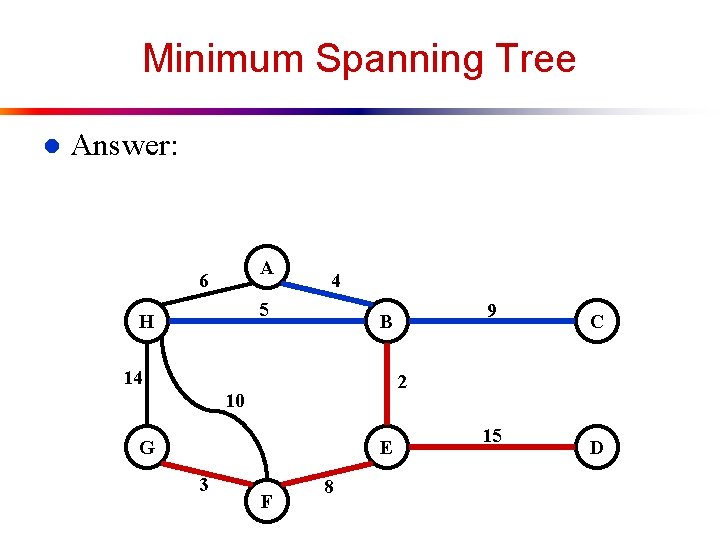
Minimum Spanning Tree l Answer: A 6 4 5 H 14 C 2 10 G E 3 9 B F 8 15 D

Minimum Spanning Tree l MSTs satisfy the optimal substructure property: an optimal tree is composed of optimal subtrees n n Let T be an MST of G with an edge (u, v) in the middle Removing (u, v) partitions T into two trees T 1 and T 2 Claim: T 1 is an MST of G 1 = (V 1, E 1), and T 2 is an MST of G 2 = (V 2, E 2) (Do V 1 and V 2 share vertices? Why? ) Proof: w(T) = w(u, v) + w(T 1) + w(T 2) (There can’t be a better tree than T 1 or T 2, or T would be suboptimal)

Minimum Spanning Tree l Thm: n n n Let T be MST of G, and let A T be subtree of T Let (u, v) be min-weight edge connecting A to V-A Then (u, v) T

Minimum Spanning Tree l Thm: n n n l Let T be MST of G, and let A T be subtree of T Let (u, v) be min-weight edge connecting A to V-A Then (u, v) T Proof: in book (see Thm 24. 1)

Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; for each u Q key[u] = ; key[r] = 0; p[r] = NULL; while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; p[r] = NULL; 3 8 while (Q not empty) Run on example graph u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; What will be the running for each u Q key[u] = ; key[r] = 0; p[r] = NULL; while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); time?

Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; What will be the running time? for each u Q key[u] = ; A: Depends on queue key[r] = 0; binary heap: O(E lg V) p[r] = NULL; Fibonacci heap: O(V lg V + E) while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

The End