Topological Sort topological order Let G V E

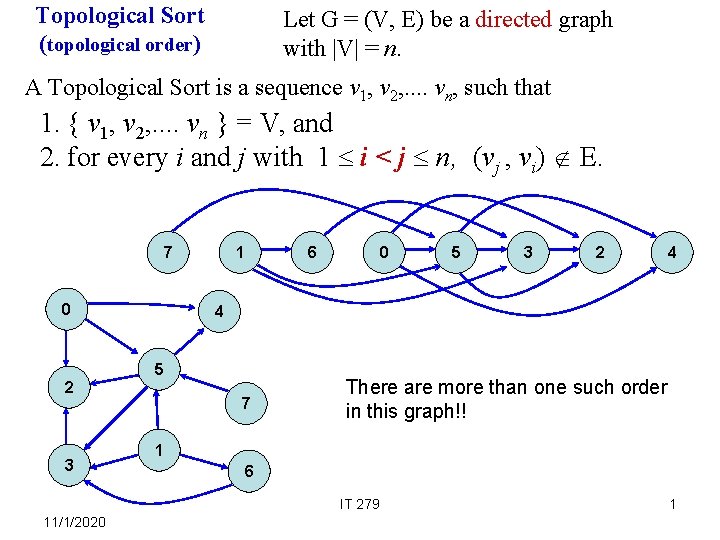
Topological Sort (topological order) Let G = (V, E) be a directed graph with |V| = n. A Topological Sort is a sequence v 1, v 2, . . vn, such that 1. { v 1, v 2, . . vn } = V, and 2. for every i and j with 1 i < j n, (vj , vi) E. 7 0 1 6 2 3 2 4 7 There are more than one such order in this graph!! 1 6 IT 279 11/1/2020 5 4 5 3 0 1

Algorithm for finding Topological Sort Principle: vertex with in-degree 0 should be listed first. 2 1 7 Algorithm: 2 7 1 Input G=(V, E) Repeat the following steps until no more vertex left: 1. Find a vertex v with in-degree 0; 2. If no such v and V is not empty, then stop the algorithm; this graph is not acyclic; 3. If such v exists, remove v from V, add v into the sequence of a topological; 4. Update E. 11/1/2020 IT 279 2

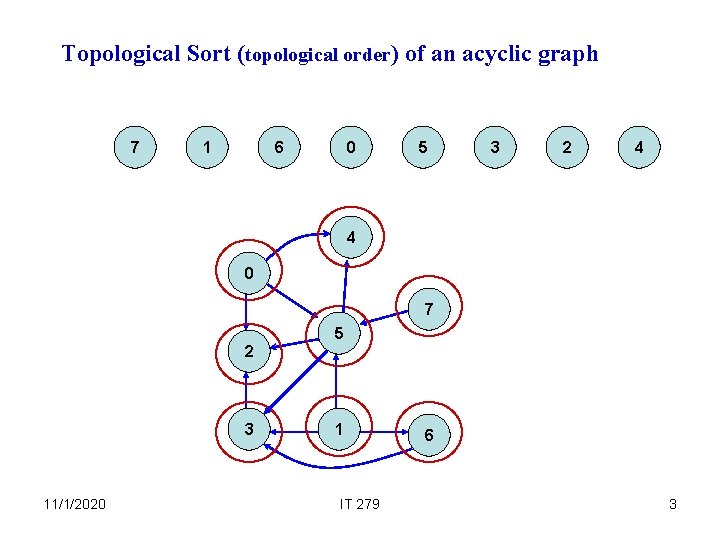
Topological Sort (topological order) of an acyclic graph 7 1 6 0 5 3 2 4 4 0 7 5 2 3 11/1/2020 1 IT 279 6 3

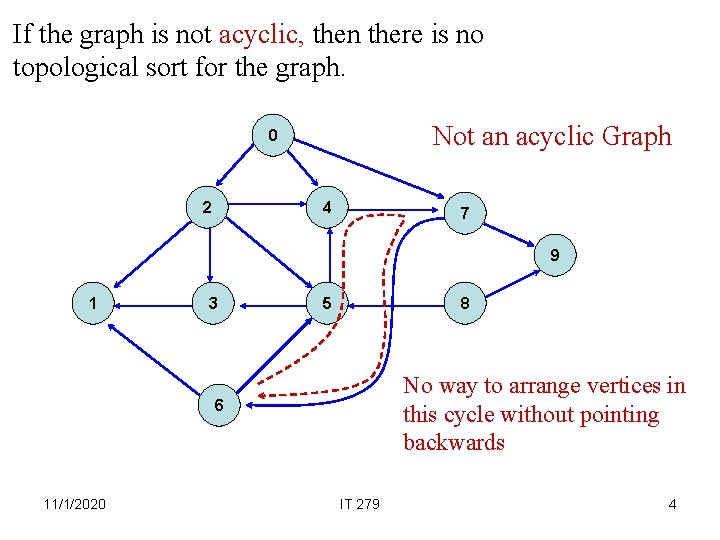
If the graph is not acyclic, then there is no topological sort for the graph. Not an acyclic Graph 0 2 4 7 9 1 3 5 8 No way to arrange vertices in this cycle without pointing backwards 6 11/1/2020 IT 279 4

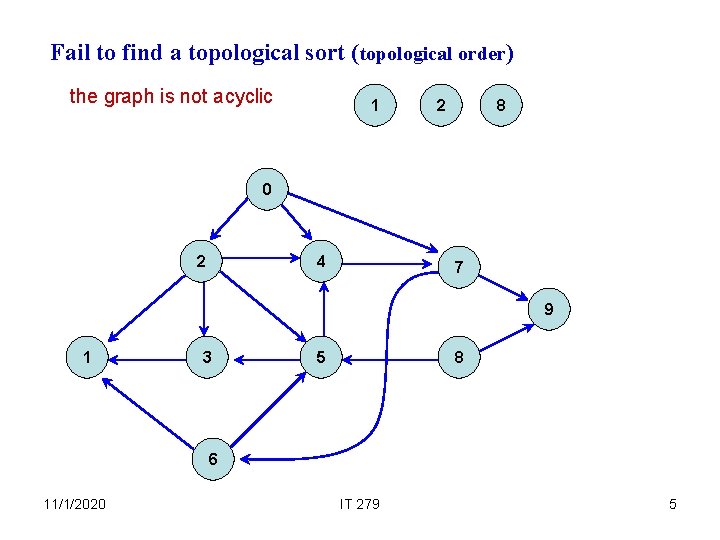
Fail to find a topological sort (topological order) the graph is not acyclic 1 2 8 0 2 4 7 9 1 3 5 8 6 11/1/2020 IT 279 5

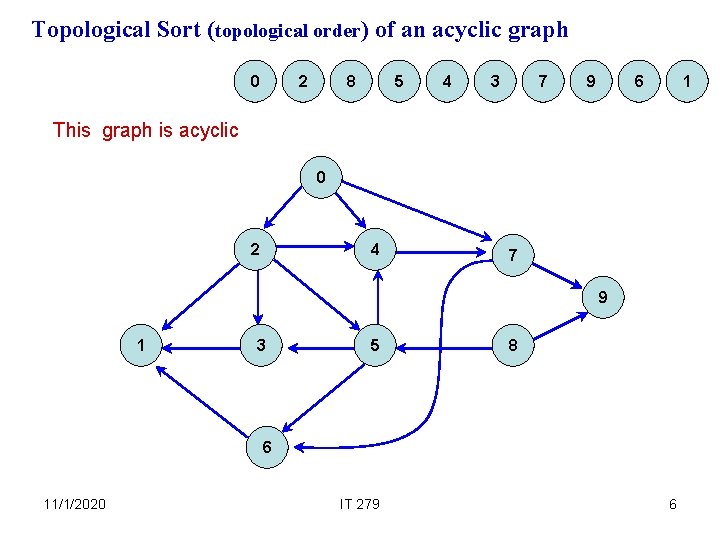
Topological Sort (topological order) of an acyclic graph 0 2 8 5 4 3 7 9 6 1 This graph is acyclic 0 2 4 7 9 1 3 5 8 6 11/1/2020 IT 279 6

Topological Sort in C++ // return an array where the first entry is the size of g // or 0 if g is not acyclic; int * graph: : topsort(const Graph & g) { int *topo; Graph temp. G = g; topo = new int[g. size()+1]; topo[0] = g. size(); for (int i=1; i<=topo[0]; i++) { int v = find. Vertexwith. Zero. In(temp. G); if (v == -1) { // g is not acyclic delete [] topo; topo = new int[1]; topo[0] = 0; return topo; } topo[i] = v; remove_v(temp. G, v); } return topo; } 11/1/2020 IT 279 7

Edsger Wybe Dijkstra 1930 -2002 • Algorithm design • Programming languages • Operating systems • Distributed processing • Formal specification and verification 1972 Turing Award “Object-oriented programming is an exceptionally bad idea which could only have originated in California. ” (Well, Sir! You can say that!) Dijkstra Algorithm: To find the shortest path between two vertices in a weighted graph. 11/1/2020 IT 279 8

Common Algorithm Techniques 1. Divide and Conquer. 2. Back Tracking. 3. Greedy Algorithms: algorithms that make decisions based on the current information; and once a decision is made, the decision will not be revised. 4. Dynamic Programming: dynamically update information and change decisions in the course of the computation. 11/1/2020 IT 279 9

Problem: Minimized the number of coins for change for 66 ¢ { 25¢, 10¢, 5¢, 1¢ } What is your strategy? 25¢ 2 50¢ 1 10¢ 5¢ 1¢ 1 1¢ 5 66¢ 16¢ We can use a greedy algorithm to obtain the minimum number of coins. 6¢ 1¢ 0¢ In general, we need dynamic programming to do the job Greedy method 11/1/2020 IT 279 10

Greedy Algorithms Dynamic Programming Problem: Minimized the number of coins for 66¢ { 25¢, 12¢, 5¢, 1¢ } 25¢ 2 50¢ 12¢ 1 12¢ 5¢ 0 0¢ 1¢ 4 4¢ 7 66¢ 16¢ 4¢ 4¢ 0¢ Greedy method 11/1/2020 25¢ 2 50¢ 12¢ 0 0¢ 5¢ 3 15¢ 1¢ 1 1¢ 6 66¢ Dynamic method IT 279 11

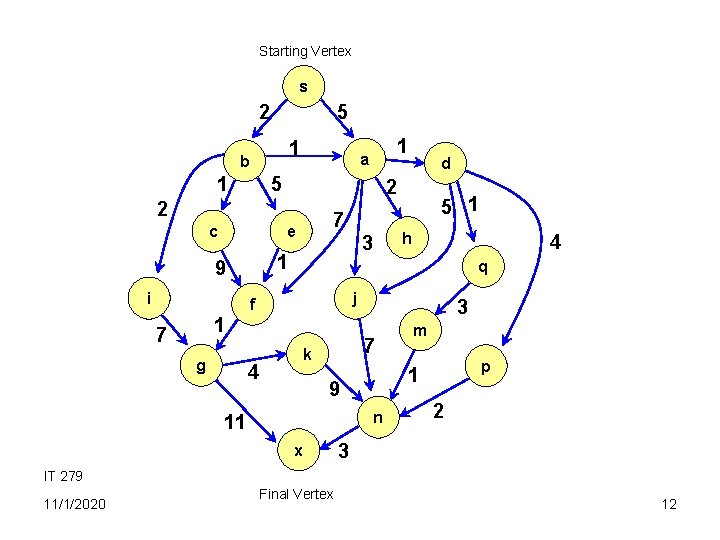
Starting Vertex s 2 5 1 b 1 5 c 7 e j 1 g 4 4 q f 7 5 1 h 3 1 9 d 2 2 i 1 a 3 7 k n x p 1 9 11 m 2 3 IT 279 11/1/2020 Final Vertex 12

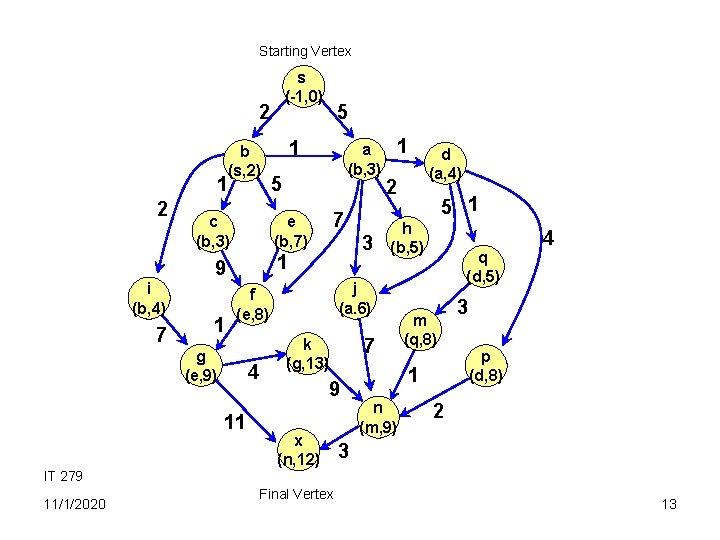
Starting Vertex s (-1, 0) 2 b (s, 2) 1 2 c (b, 3) 7 1 5 7 3 4 1 9 x (n, 12) Final Vertex 5 1 h (b, 5) 7 k (g, 13) d (a, 4) 2 j (a. 6) f (e, 8) 11 11/1/2020 a (b, 3) 1 g (e, 9) IT 279 1 e (b, 7) 9 i (b, 4) 5 q (d, 5) m (q, 8) 1 n (m, 9) 4 3 p (d, 8) 2 3 13

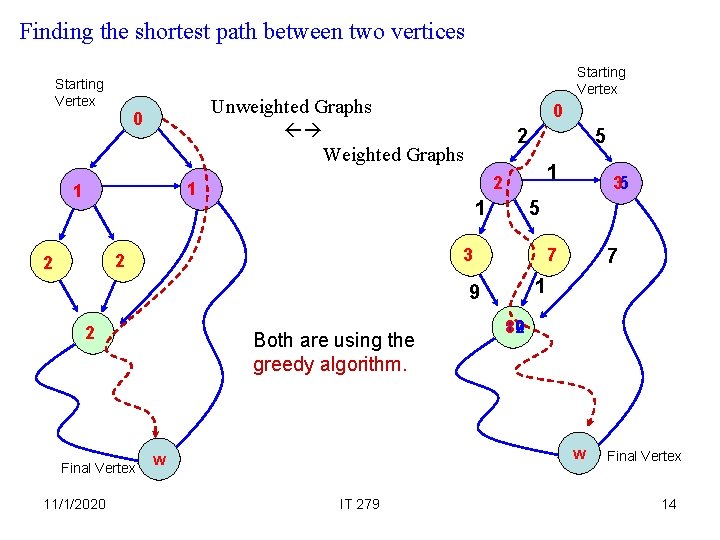
Finding the shortest path between two vertices Starting Vertex Unweighted Graphs Weighted Graphs 0 0 2 1 7 Final Vertex 11/1/2020 Both are using the greedy algorithm. 7 1 9 2 35 5 3 2 2 1 1 5 12 8 10 w w IT 279 Final Vertex 14

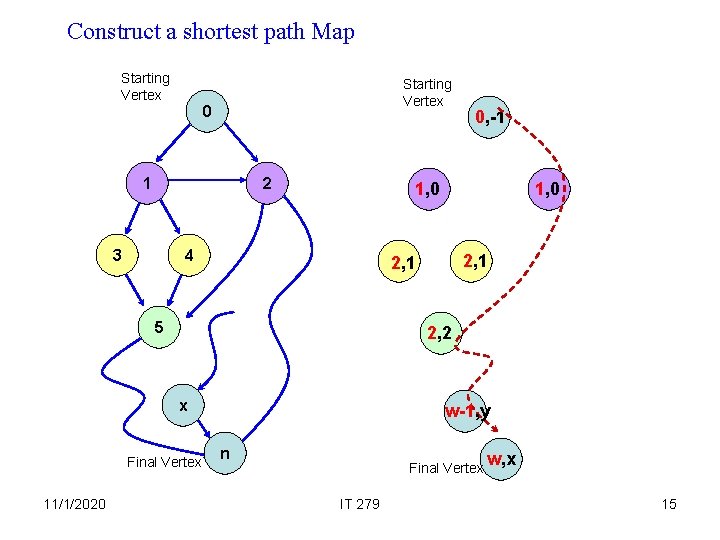
Construct a shortest path Map Starting Vertex 0 1 2 3 1, 0 4 1, 0 2, 1 5 2, 2 x Final Vertex 11/1/2020 0, -1 w-1, y n Final Vertex IT 279 w, x 15

Shortest paths of unweighted graphs // <vertex, <distance, previous vertex in the path>> typedef map<int, pair<double, int> > Path. Map; Path. Map graph: : Unweighted. Shortest. Path(Graph & g, int s) { Path. Map SPMap; // create a bookkeeper; for (Graph: : iterator itr = g. begin(); itr != g. end(); itr++) { SPMap[itr->first] = make_pair(inft, -1); // -1 mean no previous } SPMap[s] = make_pair(0, -1); // s is not done yet. deque<int> candidates; candidates. push_back(s); while (!candidates. empty()) { int v = candidates[0]; candidates. pop_front(); Adjacency. List ADJ = g[v]; for (Adjacency. List: : iterator w=ADJ. begin(); w != ADJ. end(); w++) { if (SPMap[w->first]. first == inft) { SPMap[w->first]. first = SPMap[v]. first+1; SPMap[w->first]. second=v; candidates. push_back(w->first); } // end enqueue next v } // end ADJ interation; all nextvs's next into the queue. } return SPMap; } 11/1/2020 IT 279 16

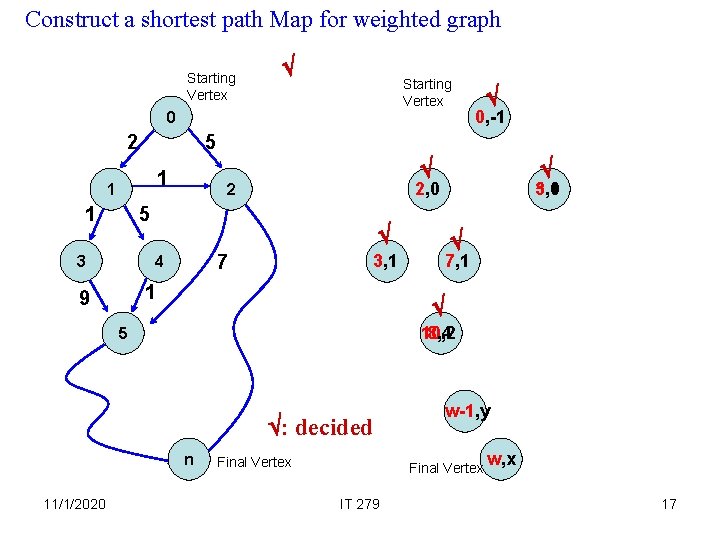
Construct a shortest path Map for weighted graph Starting Vertex 0 2 5 1 1 1 7, 1 10, 2 8, 4 5 : decided n 11/1/2020 5, 0 3, 1 7 1 9 2, 0 2 4 0, -1 5 3 Final Vertex w-1, y Final Vertex IT 279 w, x 17

Shortest paths of weighted graphs (I) // A Dijkstra's algorithm Path. Map graph: : Shortest. Path(Graph & g, int s) { Path. Map SPMap; map<int, pair<double, bool> > dist_map; // A distance map // for book keeping; for (Graph: : iterator itr = g. begin(); itr != g. end(); itr++) { dist_map[itr->first] = make_pair(inft, false); SPMap[itr->first] = make_pair(inft, -1); } dist_map[s] = make_pair(0, false); // s is not done yet. multimap<double, int> candidates ; // next possible vertices //sorted by their distance. candidates. insert(make_pair(0, s)); // start from s; . . } 11/1/2020 IT 279 18

// A Dijkstra's algorithm Path. Map graph: : Shortest. Path(Graph & g, int s) {. . . while (! candidates. empty()) { int v = candidates. begin()->second; double costs 2 v = candidates. begin()->first; candidates. erase(candidates. begin()); if (dist_map[v]. second) continue; // v is done after pair // (weight v) is inserted; dist_map[v] = make_pair(costs 2 v, true); Adjacency. List ADJ = g[v]; // all not done adjacent vertices // should be candidates for (Adjacency. List: : iterator itr=ADJ. begin(); itr != ADJ. end(); itr++) { int w = itr->first; if (dist_map[w]. second) continue; // this w is done; double cost_via_v = costs 2 v + itr->second; if (cost_via_v < dist_map[w]. first) { dist_map[w] = make_pair(cost_via_v , false); SPMap[w] = make_pair(cost_via_v, v); } candidates. insert(make_pair(cost_via_v, w)); } // end for ADJ iteration; } // end while !candidates. empty() return SPMap; } Shortest paths (II) 11/1/2020 IT 279 19