Lecture 16 DFS DAG and Strongly Connected Components

Lecture 16: DFS, DAG, and Strongly Connected Components Shang-Hua Teng

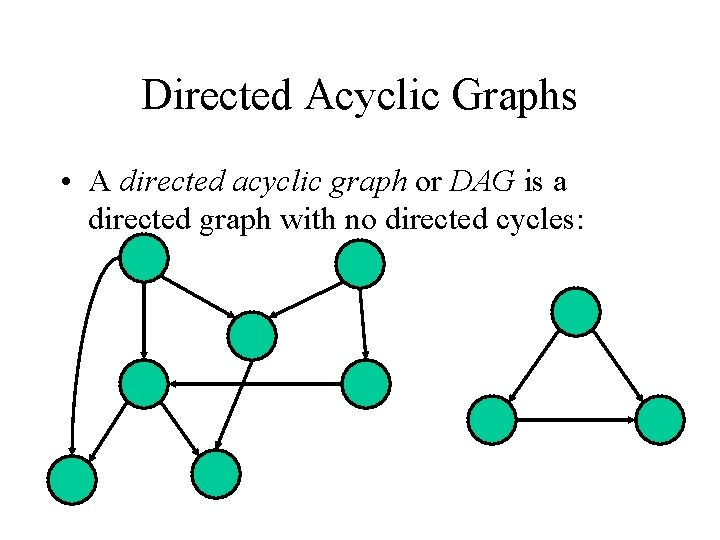
Directed Acyclic Graphs • A directed acyclic graph or DAG is a directed graph with no directed cycles:

DFS and DAGs • Theorem: a directed graph G is acyclic iff a DFS of G yields no back edges: – => if G is acyclic, will be no back edges • Trivial: a back edge implies a cycle – <= if no back edges, G is acyclic • Proof by contradiction: G has a cycle a back edge – Let v be the vertex on the cycle first discovered, and u be the predecessor of v on the cycle – When v discovered, whole cycle is white – Must visit everything reachable from v before returning from DFS-Visit() – So path from u v is gray, thus (u, v) is a back edge

Topological Sort • Topological sort of a DAG: – Linear ordering of all vertices in graph G such that vertex u comes before vertex v if edge (u, v) G • Real-world application: Scheduling a dependent graph, find a feasible course plan for university studies

A Topological Sort Algorithm Topological-Sort() { 1. Call DFS to compute finish time f[v] for each vertex 2. As each vertex is finished, insert it onto the front of a linked list 3. Return the linked list of vertices } • Time: O(V+E) • Correctness: need to prove that (u, v) G f[u]>f[v]

Correctness of Topological Sort • Lemma: (u, v) G f[u] > f[v] – When (u, v) is explored, u is gray, consider the following cases: 1. v is gray (u, v) is back edge. Can’t happen, if G is a DAG. 2. v if white v becomes descendent of u f[v] < f[u] (since must finish v before backtracking and finishing u) 3. v is black v already finished f[v] < f[u]

Our Algorithm for Topological Sorting is correct

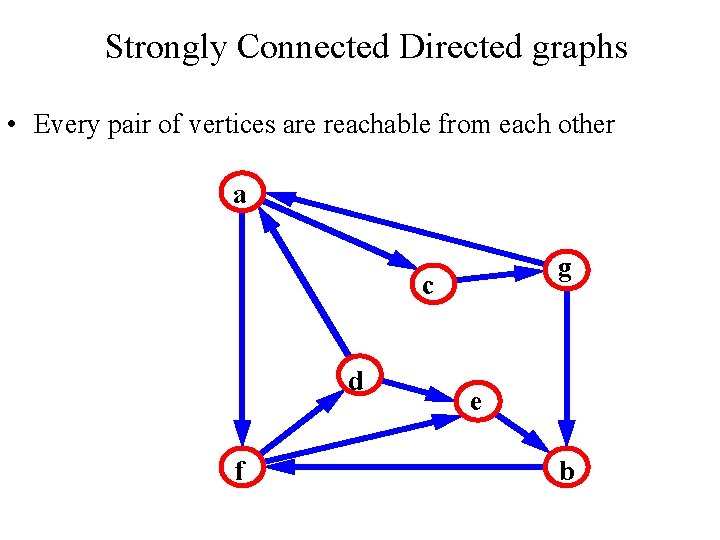
Strongly Connected Directed graphs • Every pair of vertices are reachable from each other a g c d f e b

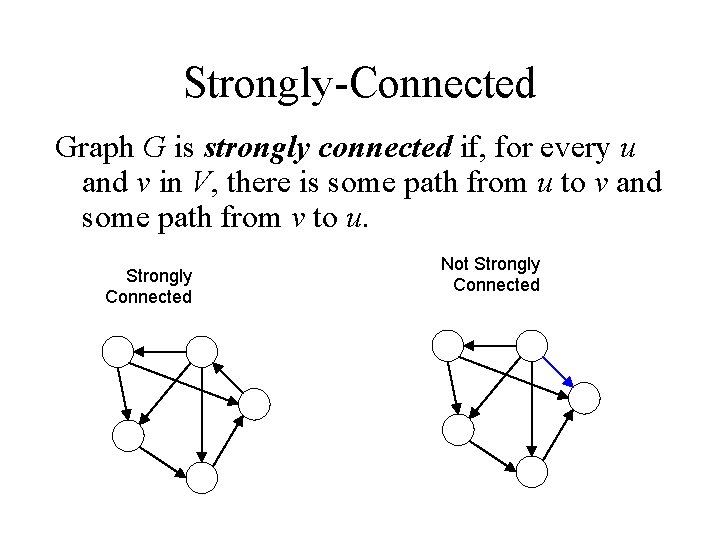
Strongly-Connected Graph G is strongly connected if, for every u and v in V, there is some path from u to v and some path from v to u. Strongly Connected Not Strongly Connected

Strongly-Connected Components A strongly connected component of a graph is a maximal subset of nodes (along with their associated edges) that is strongly connected. Nodes share a strongly connected component if they are inter-reachable.

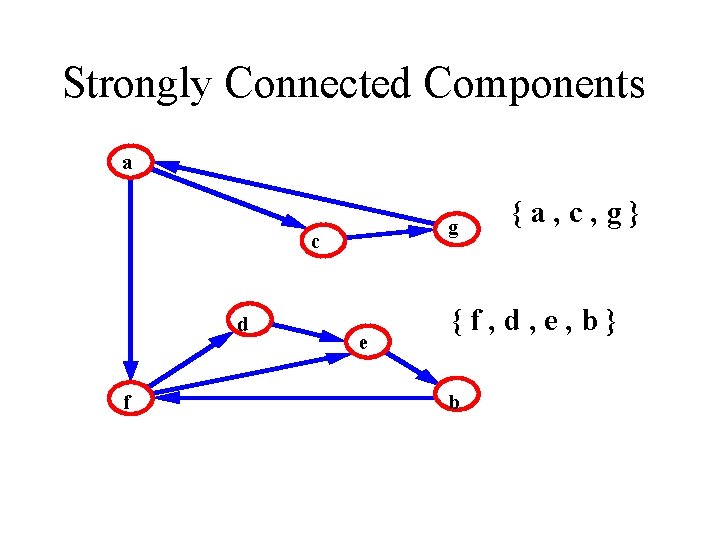
Strongly Connected Components a g c d f e {a, c, g} {f, d, e, b} b

Reduced Component Graph of Strongly Connected Components a g c d f {a, c, g} {f, d, e, b} e b • Component graph GSCC=(VSCC, ESCC): one vertex for each component – (u, v) ESCC if there exists at least one directed edge from the corresponding components

Strongly Connected Components

Graph of Strongly Connected Components • Theorem: the Component graph GSCC=(VSCC, ESCC) is a DAG – Each component is maximal in the sense that no other vertices can be added to it. If GSCC=(VSCC, ESCC) is not a DAG, then one can merge components on along a circle of GSCC • Therefore, GSCC has a topological ordering

Finding Strongly-Connected Components • Input: A directed graph G = (V, E) • Output: a partition of V into disjoint sets so that each set defines a strongly connected component of G • How should we compute the partition?

Graph of Strongly Connected Components • Recall: Theorem: the Component graph GSCC=(VSCC, ESCC) is a DAG – Each component is maximal in the sense that no other vertices can be added to it. If GSCC=(VSCC, ESCC) is not a DAG, then one can merge components on along a circle of GSCC • Therefore, GSCC has a topological ordering

DFS on G Topological Sort GSCC=(VSCC, ESCC) • Let U be a subset of V • If we output U in VSCC in the decreasing order of f[U], then we topologically sort GSCC • Lemma: Let U and U’ be distinct strongly connected component, suppose there is an edge (u, v) in E where u in U and v in U’. Then f[U] > f[U’]

Proof of the Lemma: Let U and U’ be distinct strongly connected component, suppose there is an edge (u, v) in E where u in U and v in U’. Then f[U] > f[U’] Proof: Two cases 1. d[U] < d[U’], say x in U is the first vertex 2. d[U’] < d[U], say y is the first, but U is not reachable from y

Transpose of a Digraph Transpose of G = (V, E): GT=(V, ET), where ET={(u, v): (v, u) E} If G is a DAG then GT is also a DAG If we print the topological order of G in the reverse order, then it is a topological order of GT

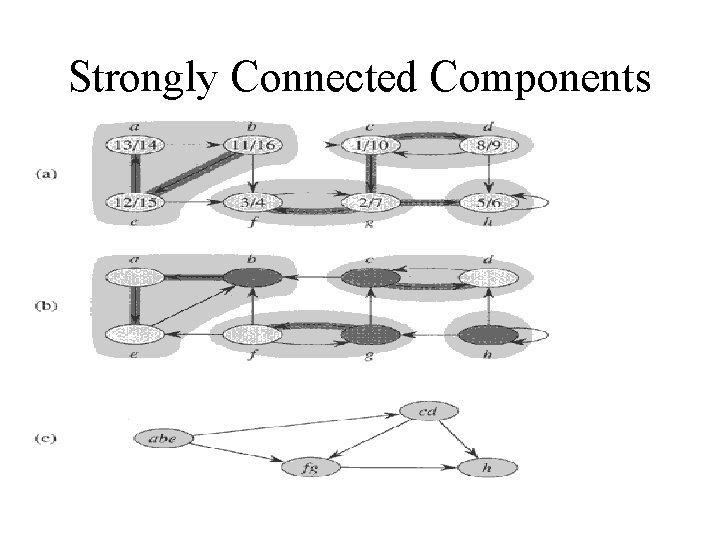
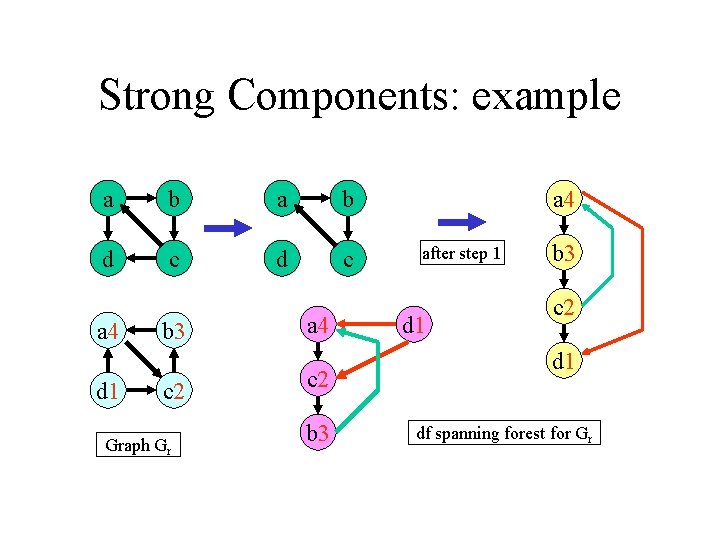
Strongly-Connected Components Strongly-Connected-Components(G) 1. call DFS(G) to compute finishing times f[u] for each vertex u. 2. compute GT 3. call DFS(GT), but in the main loop of DFS, consider the vertices in order of decreasing f[u] 4. output the vertices of each tree in the depth-first forest of step 3 as a separate strongly connected component. The graph GT is the transpose of G, which is visualized by reversing the arrows on the digraph.

Strong Components: example a b d c a 4 d 1 b 3 c 2 Graph Gr a 4 c 2 b 3 a 4 after step 1 d 1 b 3 c 2 d 1 df spanning forest for Gr

Runtime Lines 1 and 3 are (E+V) due to DFS Line 2 involves creating an adjacency list or matrix, and it is also O(E+V) Line 4 is constant time So, SCC(G) is (E+V)

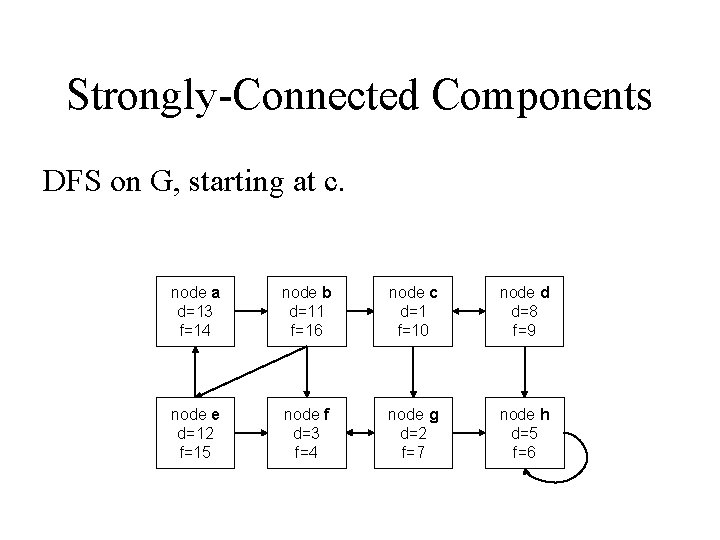
Strongly-Connected Components DFS on G, starting at c. node a d=13 f=14 node b d=11 f=16 node c d=1 f=10 node d d=8 f=9 node e d=12 f=15 node f d=3 f=4 node g d=2 f=7 node h d=5 f=6

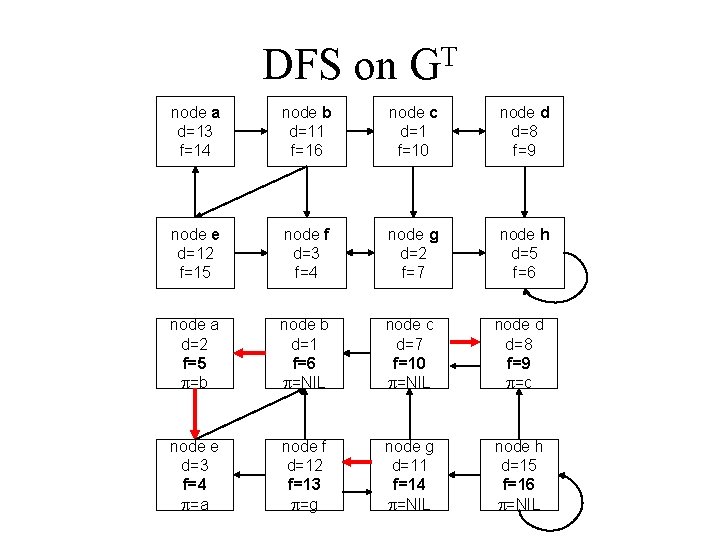
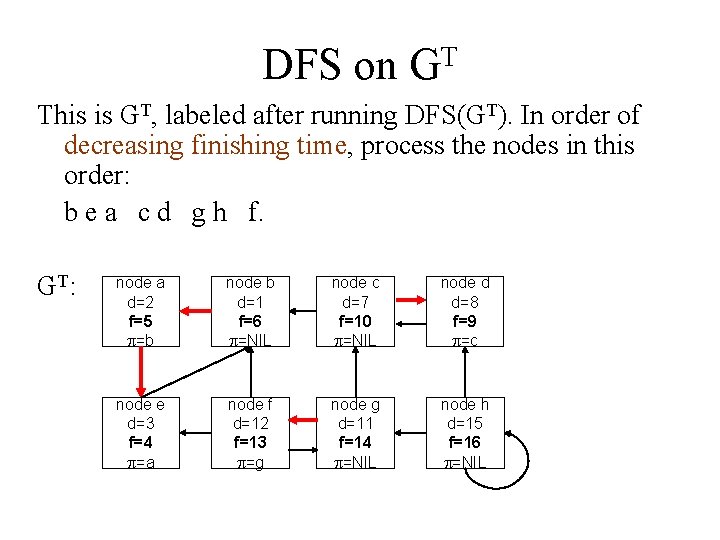
DFS on GT node a d=13 f=14 node b d=11 f=16 node c d=1 f=10 node d d=8 f=9 node e d=12 f=15 node f d=3 f=4 node g d=2 f=7 node h d=5 f=6 node a d=2 f=5 =b node b d=1 f=6 =NIL node c d=7 f=10 =NIL node d d=8 f=9 =c node e d=3 f=4 =a node f d=12 f=13 =g node g d=11 f=14 =NIL node h d=15 f=16 =NIL

DFS on GT This is GT, labeled after running DFS(GT). In order of decreasing finishing time, process the nodes in this order: b e a c d g h f. GT : node a d=2 f=5 =b node b d=1 f=6 =NIL node c d=7 f=10 =NIL node d d=8 f=9 =c node e d=3 f=4 =a node f d=12 f=13 =g node g d=11 f=14 =NIL node h d=15 f=16 =NIL

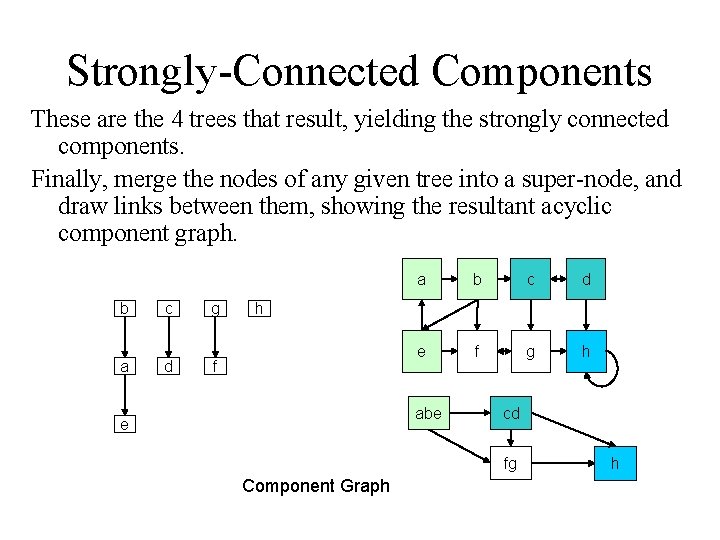
Strongly-Connected Components These are the 4 trees that result, yielding the strongly connected components. Finally, merge the nodes of any given tree into a super-node, and draw links between them, showing the resultant acyclic component graph. b c g a d f a b c d e f g h h abe e cd fg Component Graph h