Topological Sort Introduction Definition of Topological Sort Topological

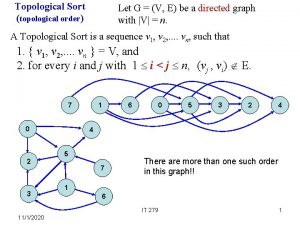
Topological Sort • Introduction. • Definition of Topological Sort. • Topological Sort is Not Unique. • Topological Sort Algorithms. • An Example. • Implementation of Source Removal Algorithm. • Review Questions. 1

Introduction • There are many problems involving a set of tasks in which some of the tasks must be done before others. • For example, consider the problem of taking a course only after taking its prerequisites. • Is there any systematic way of linearly arranging the courses in the order that they should be taken? Yes! - Topological sort. 2

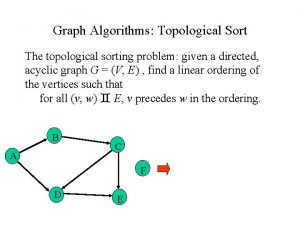
What is a DAG? • A directed acyclic graph (DAG) is a directed graph without cycles. Example: • DAGs arrise in modeling many problems that involve prerequisite constraints (construction projects, course prerequisites, document version control, compilers, etc. ) • Some properties of DAGs: – Every DAG must have at least one vertex with in-degree zero and at least one vertex with out-degree zero • A vertex with in-degree zero is called a source vertex, a vertex with outdegree zero is called a sink vertex. – G is a DAG iff each vertex in G is in its own strongly connected component – Every edge (v, w) in a DAG G has finishing. Time[w] < finishing. Time[v] in a DFS traversal of G 3

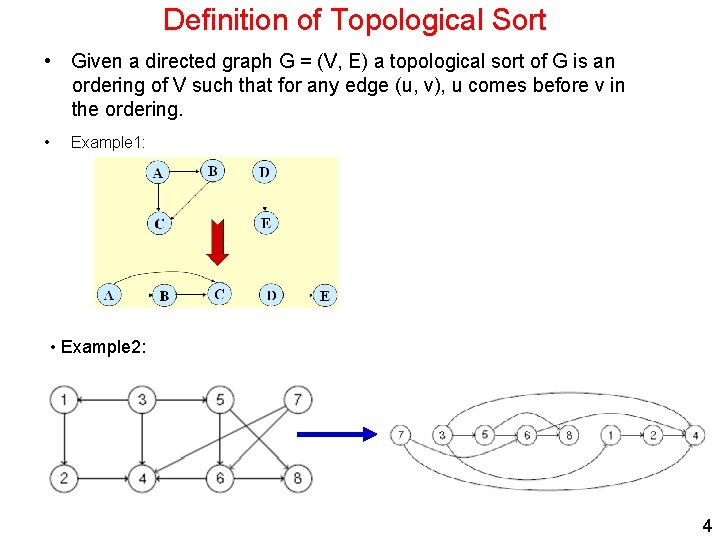
Definition of Topological Sort • Given a directed graph G = (V, E) a topological sort of G is an ordering of V such that for any edge (u, v), u comes before v in the ordering. • Example 1: • Example 2: 4

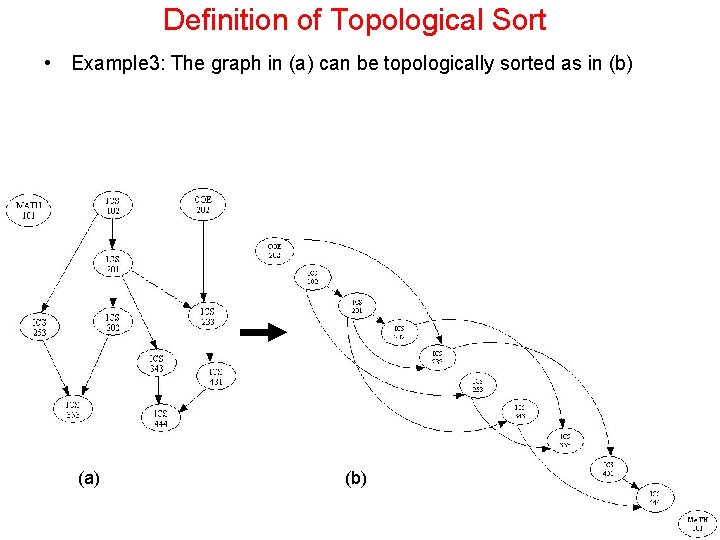
Definition of Topological Sort • Example 3: The graph in (a) can be topologically sorted as in (b) (a) (b) 5

Topological Sort is not unique • Topological sort is not unique. • The following are all topological sort of the graph below: s 1 = {a, b, c, d, e, f, g, h, i} s 2 = {a, c, b, f, e, d, h, g, i} s 3 = {a, b, d, c, e, g, f, h, i} s 4 = {a, c, f, b, e, h, d, g, i} etc. 6

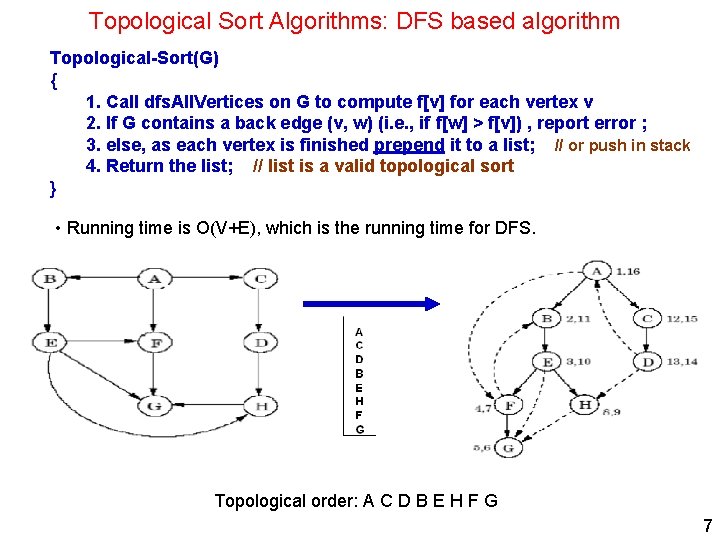
Topological Sort Algorithms: DFS based algorithm Topological-Sort(G) { 1. Call dfs. All. Vertices on G to compute f[v] for each vertex v 2. If G contains a back edge (v, w) (i. e. , if f[w] > f[v]) , report error ; 3. else, as each vertex is finished prepend it to a list; // or push in stack 4. Return the list; // list is a valid topological sort } • Running time is O(V+E), which is the running time for DFS. Topological order: A C D B E H F G 7

Topological Sort Algorithms: Source Removal Algorithm • The Source Removal Topological sort algorithm is: – Pick a source u [vertex with in-degree zero], output it. – Remove u and all edges out of u. – Repeat until graph is empty. int topological. Order. Traversal( ){ int num. Visited. Vertices = 0; while(there are more vertices to be visited){ if(there is no vertex with in-degree 0) break; else{ select a vertex v that has in-degree 0; visit v; num. Visited. Vertices++; delete v and all its emanating edges; } } return num. Visited. Vertices; } 8

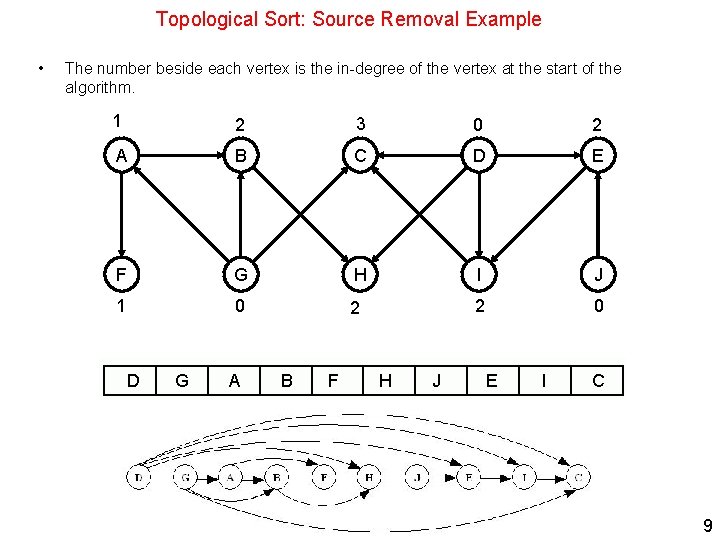
Topological Sort: Source Removal Example • The number beside each vertex is the in-degree of the vertex at the start of the algorithm. 1 2 3 0 2 A B C D E F G H I J 1 0 2 2 0 D G A B F H J E I C 9

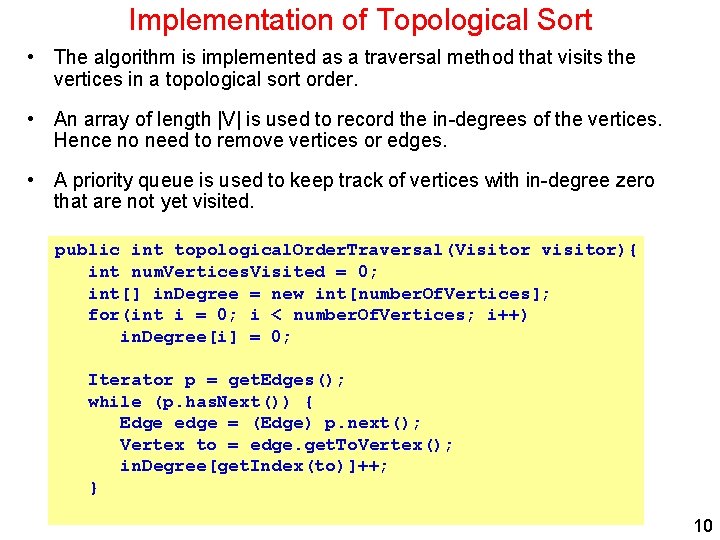
Implementation of Topological Sort • The algorithm is implemented as a traversal method that visits the vertices in a topological sort order. • An array of length |V| is used to record the in-degrees of the vertices. Hence no need to remove vertices or edges. • A priority queue is used to keep track of vertices with in-degree zero that are not yet visited. public int topological. Order. Traversal(Visitor visitor){ int num. Vertices. Visited = 0; int[] in. Degree = new int[number. Of. Vertices]; for(int i = 0; i < number. Of. Vertices; i++) in. Degree[i] = 0; Iterator p = get. Edges(); while (p. has. Next()) { Edge edge = (Edge) p. next(); Vertex to = edge. get. To. Vertex(); in. Degree[get. Index(to)]++; } 10

Implementation of Topological Sort Binary. Heap queue = new Binary. Heap(number. Of. Vertices); p = get. Vertices(); while(p. has. Next()){ Vertex v = (Vertex)p. next(); if(in. Degree[get. Index(v)] == 0) queue. enqueue(v); } while(!queue. is. Empty() && !visitor. is. Done()){ Vertex v = (Vertex)queue. dequeue. Min(); visitor. visit(v); num. Vertices. Visited++; p = v. get. Successors(); while (p. has. Next()){ Vertex to = (Vertex) p. next(); if(--in. Degree[get. Index(to)] == 0) queue. enqueue(to); } } return num. Vertices. Visited; } 11

Review Questions 1. List the order in which the nodes of the directed graph GB are visited by 2. topological order traversal that starts from vertex a. Use both DFS-based and Source Removal algorithm 2. What kind of DAG has a unique topological sort? 3. Generate a directed graph using the required courses for your major. Now apply topological sort on the directed graph you obtained. 12