Minimum Spanning Tree Given a graph G V

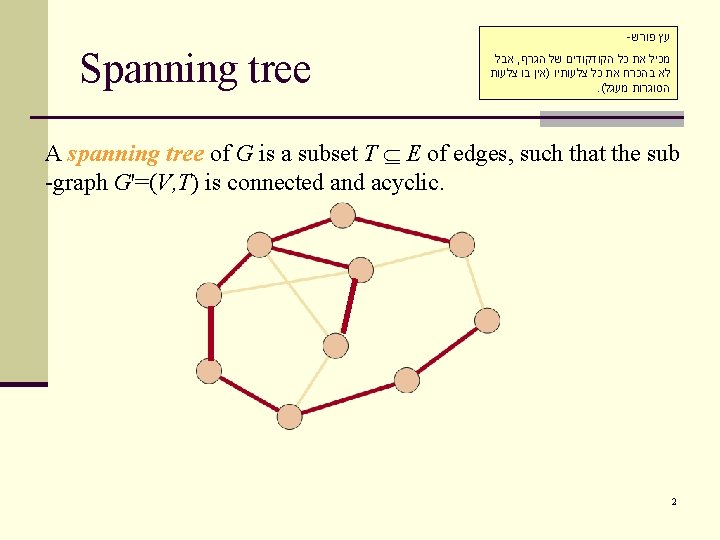
- עץ פורש מינימלי Minimum Spanning Tree Given a graph G = (V, E) and an assignment of weights w(e) to the edges of G, a minimum spanning tree T of G is a spanning tree with minimum total edge weight הוא עץ פורש שסכום המשקולות על הצלעות שלו הוא מינימלי (MST) 1 3 3 6 6 9 7 8 1 3 2 7 5 4 3

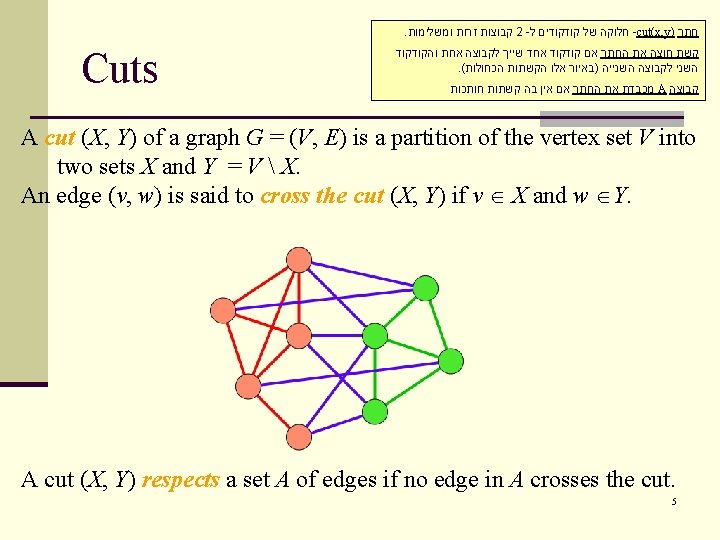
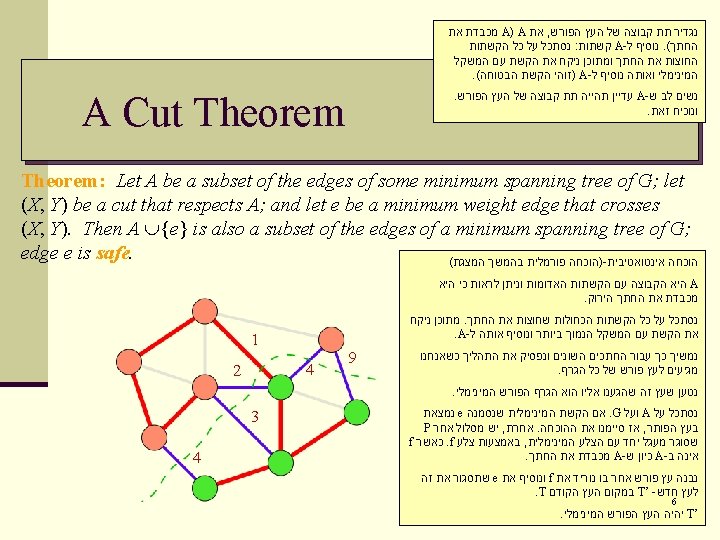
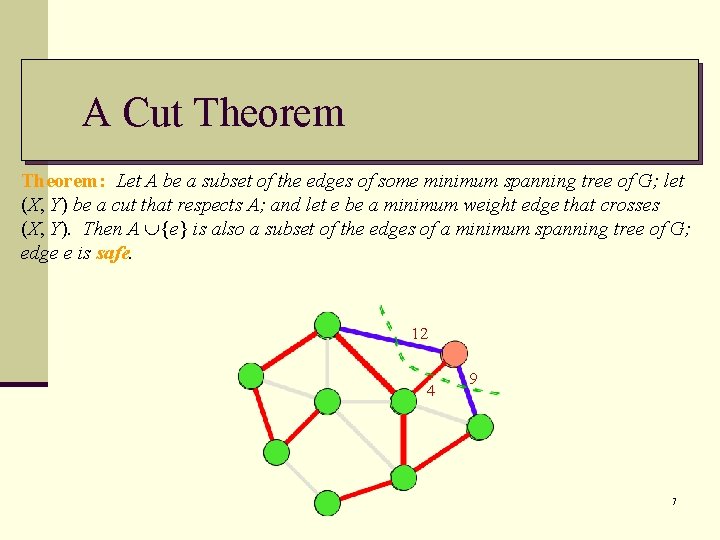
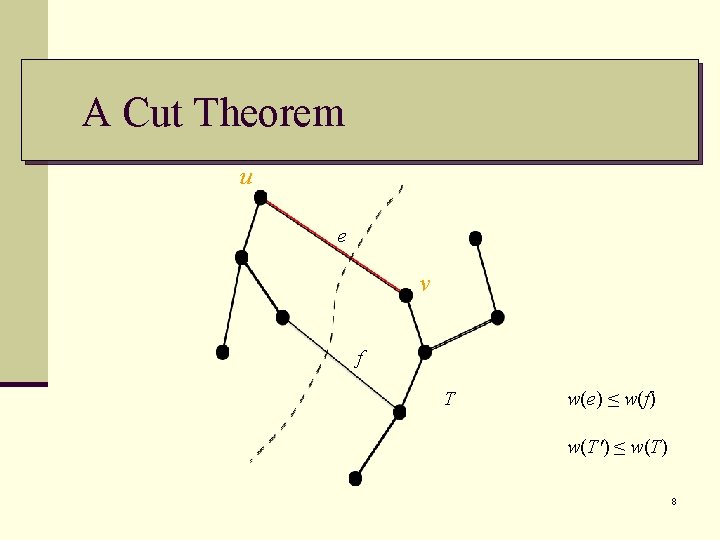
A Cut Theorem: Let A be a subset of the edges of some minimum spanning tree of G; let (X, Y) be a cut that respects A; and let e be a minimum weight edge that crosses (X, Y). Then A {e} is also a subset of the edges of a minimum spanning tree of G; edge e is safe. 12 4 9 7

A Cut Theorem u e v f T w(e) ≤ w(f) w(T') ≤ w(T) 8

Proof: n Let T be a MST such that A T. n If e = (u, v) T, add e to T. n The edge e = (u, v) forms a cycle with edges on the path p from u to v in T. Since u and v are on opposite sides of the cut, there is at least one edge f = (x, y) in T on the path p that also crosses the cut. n f A since the cut respects A. Since f is on the unique path from u to v in T, removing it breaks T into two components. n w(e) ≤ w(f) (why? ) n Let T ' = T – {f} {e} w(T ') ≤ w(T). 9

A Cut Theorem Corollary: Let G=(V, E) be a connected undirected graph and A a subset of E included in a minimum spanning tree T for G, and let C=(VC, EC) be a tree in the forest GA=(V, A). If e is a light edge connecting C to some other component in GA, then e is safe for A. Proof: The cut (VC, V–VC) respects A, and e is a light edge for this cut. Therefore, e is safe. 10

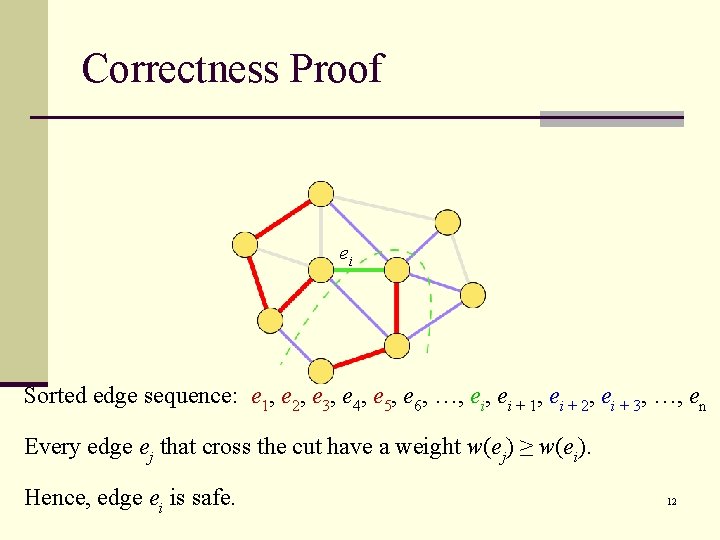
Correctness Proof ei Sorted edge sequence: e 1, e 2, e 3, e 4, e 5, e 6, …, ei + 1, ei + 2, ei + 3, …, en Every edge ej that cross the cut have a weight w(ej) ≥ w(ei). Hence, edge ei is safe. 12

קודקודים שייכים לאותו רכיב 2 כדי לדעת אם union-find נעזר במבנה הנתונים , קשירות Union-Find Data Structures n. Given a set S of n elements, maintain a partition of S into subsets S 1, S 2, …, Sk n. Support the following operations: n. Union(x, y): Replace sets Si and Sj such that x Si and y Sj with Si Sj in the current partition n. Find(x): Returns a member r(Si) of the set Si that contains x n. In particular, Find(x) and Find(y) return the same element if and only if x and y belong to the same set. n. It is possible to create a data structure that supports the above operations in O(α(n)) amortized time, where α is the inverse תחזיר α(n) הערכים מאוד קטנים לכן Ackermann function. 5 מקסימום 13

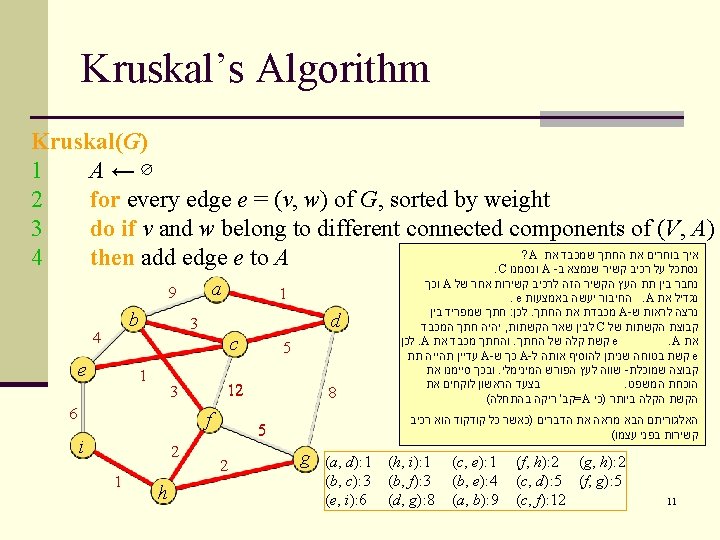
Kruskal’s Algorithm Using Union. Find Data Structure Kruskal(G, w) A for each vertex v V do Make-Set(v) sort the edges in E in non-decreasing weight order w for each edge (u, v) E do if Find-Set(u) ≠ Find-Set(v) then A A {(u, v)} Union(u, v) return A 14

Kruskal’s Algorithm Using Union. Find Data Structure בהנחה שאנו יודעים לממש את ? מהו זמן הריצה שלו , האלגוריתם זמן מינימלי למיון קשתות n. Analysis: n. O(|E| log |E|) time for everything except the operations on S n. Cost of operations on S: n. O(α(|E|, |V|)) amortized time per operation on S n|V| – 1 Union operations n|E| Find operations סה"כ לאחר מיון הקשתות לא n. Total: O((|V| + |E|)α(|E|, |V|)) running time כולל מתנהגת α - כיון ש n. Total running time: O(|E| lg |E|). כמעט כמו קבוע : נקבל שבסה"כ 15

Union/Find נסתכל על הפעולות על מבנה הנתונים ונבין מה זמן הריצה שלהן n Assumptions: The Sets are disjoint. n Each set is identified by a representative of the set. n Initial state: n A union/find structure begins with n elements, each considered to be a one element set. n Functions: תומך בפעולות n Make-Set(x): Creates a new set with element x in it. n Union(x, y): Make one set out of the sets containing x and y. n Find-Set(x): Returns a pointer to the representative of the set מחזירים נציג של containing x. הקבוצה n 16

Basic Notation n The elements in the structure will be numbered 0 to n-1 n Each set will be referred to by the number of one of the element it contains נמספר את n Initially we have sets S , …, S 0 1 n-1 האיברים n If we were to call Union(S 2, S 4), these sets would be removed from the list, and the new set would now be called either S 2 or S 4 נסמן n Notations: n n Make-Set operations n m total operations n n m עברנו לקבוצות כי הרעיון הזה עוזר לפתור עוד בעיות מלבד זו שראינו בשיעור הקודם 17

מה יהיה זמן הריצה במצב ? זה Analysis n The worst-case analysis: n n Find(i) takes O(1) time Union(Si, Sj) takes (n) time עוברים על כל איברי המערך n A sequence of n Unions will take (n 2) time לוקחים סדרה כדי לקבל סיבוכיות לשיעורין 19

מה יהיה זמן הריצה במצב ? זה Analysis n The worst-case analysis: n n n Find(i) takes O(1) time Make-Set(i) takes O(1) time Union(Si, Sj) takes (n) time (Why? ) n/2 כי צריך לעבור בממוצע על איברים n A sequence of n Unions-Find will take (n 2) time (Example? ). פעולות n עשינו . union-find של Θ(n 2) פעולות שלוקחות סה"כ O(n) עכשיו Make-set : נבצע את פעולות האיחוד עד הסוף union(x 2, x 1) n-1 union(x 3, x 2) פעולות … union(xn, xn-1) n*O(1) + (n-1) Θ(n) =( O(n) + O(n 2) ) / 2 = Θ(n 2) Make-set union נחלק במס' הפעולות : זמן הריצה לשיעורין 21

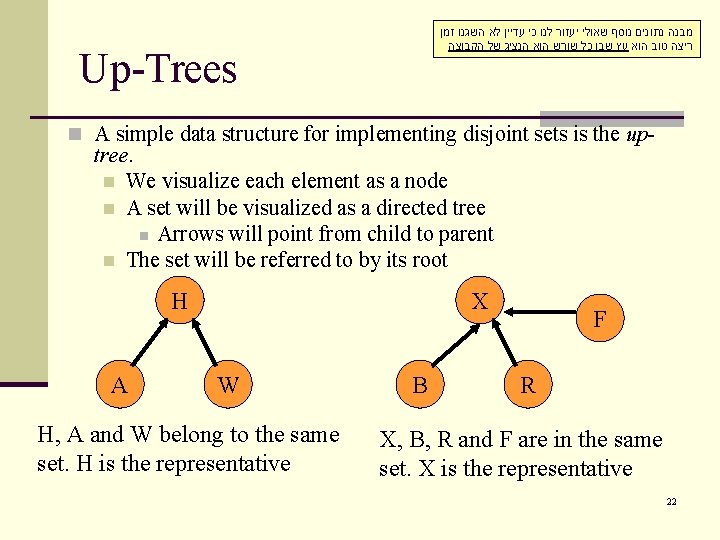
מבנה נתונים נוסף שאולי יעזור לנו כי עדיין לא השגנו זמן ריצה טוב הוא עץ שבו כל שורש הוא הנציג של הקבוצה Up-Trees n A simple data structure for implementing disjoint sets is the up- tree. n We visualize each element as a node n A set will be visualized as a directed tree n Arrows will point from child to parent n The set will be referred to by its root H A X W H, A and W belong to the same set. H is the representative B F R X, B, R and F are in the same set. X is the representative 22

Operations in Up-Trees נראה את הפעולות על העץ Follow pointer to representative element. find(x) { האב של -P(x) x if (x≠p(x)) // not the representative then p(x) find(p(x)); return p(x); } 23

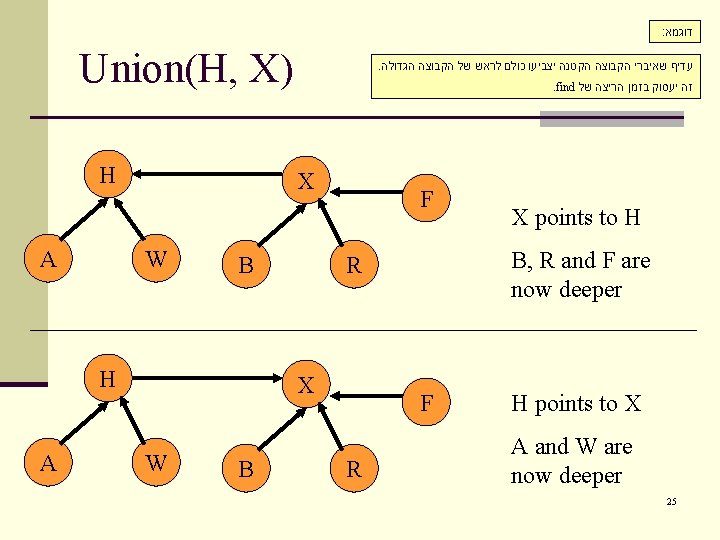
Union n Union is more complicated. n Make one representative element point to the other, but which way? Does it matter? 24

A worst case for Union can be done in O(1), but may cause find to become O(n) A B C D E Consider the result of the following sequence of operations: Union (A, B) Union (C, A) Union (D, C) Union (E, D) E : נקבל עץ מנוון D C B A וזה לא עזר לנו לגבי זמן הריצה 26

נבחן ייצוג של עץ הפוך באמצעות מערך Array Representation of Up-tree n Assume each element is associated with an integer i=0…n-1. From now on, we deal only with i. n Create an integer array, A[n] n An array entry is the element’s parent n A -1 entry signifies that element i is the representative element. במקום של הנציג נשים. כל איבר נמצא במקום שלו . -1 27

? איך מתבצעות הפעולות בייצוג הזה Array Representation of Up-tree Now the union algorithm might be: Union(x, y) { A[y] = x; // attaches y to x } The find algorithm would be find(x) { if (A[x] < 0) הגענו לשורש return(x); נחפש את מי else שנמצא באותו בתא ) מקום במערך return(find(A[x])); שמור האינדקס של ( האבא } Performance: ? ? ? דוגמא למימוש יש בהמשך 28

Analysis מה יהיה זמן הריצה במצב ? זה n Worst case: Union(Si, Sj) take O(1) time נשים לב שעדיין לא השגנו זמן ריצה טוב n Find(i) takes O(n) time n Can we do better in an amortized analysis? n What is the maximum amount of time n operations could take us? n Suppose we perform n/2 unions followed by n/2 finds n The n/2 unions could give us one tree of height n/2 -1 2 n Thus the total time would be n/2 + (n/2) = O(n ) n This strategy doesn’t really help… n 29