Section 4 1 Maximum and Minimum Values AP

Section 4. 1 Maximum and Minimum Values AP Calculus October 20, 2009 Berkley High School, D 1 B 1 todd 1@toddfadoir. com Calculus, Section 4. 1

Max and Min n n Of course they can’t be too easy; this IS calculus. Absolute Maximum: f has an absolute maximum if there exists a c such that f(c)≥f(x), for x in D. f(c) is called the maximum value. Absolute Minimum: f has an absolute minimum if there exists a c such that f(c)≤f(x), for x in D. f(c) is called the minimum value. The absolute max and absolute min are called the extremes. Calculus, Section 4. 1 2

Max and Min n Local Maximum: f has a local maximum if there exists a c such that f(c)≥f(x), for all x near c. ¨ How n n close to c? Calculus close. Local Minimum: f has a local minimum if there exists a c such that f(c)≤f(x), for all x near c. Endpoints of closed intervals can not be local maximums or minimums. Calculus, Section 4. 1 3

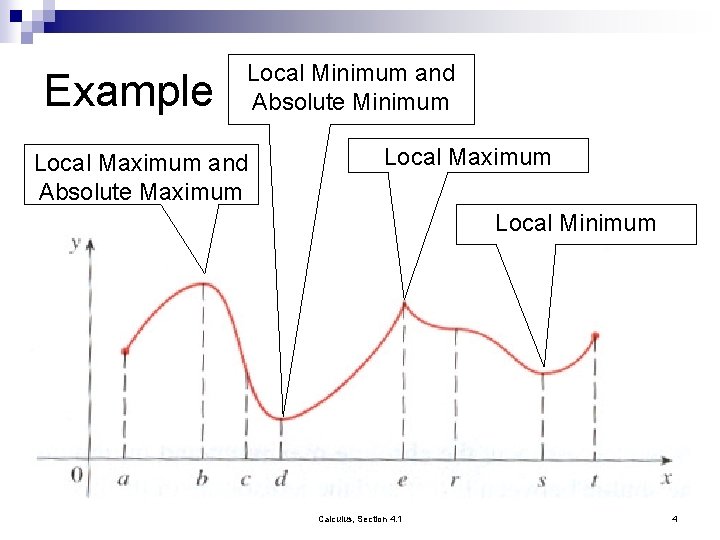
Example Local Minimum and Absolute Minimum Local Maximum and Absolute Maximum Local Minimum Calculus, Section 4. 1 4

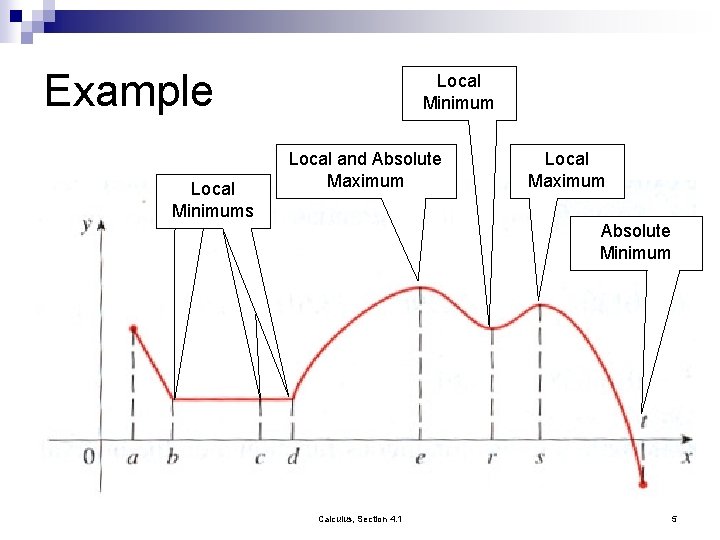
Example Local Minimums Local Minimum Local and Absolute Maximum Local Maximum Absolute Minimum Calculus, Section 4. 1 5

Example Local Maximum Local and Absolute Maximum Absolute Minimum Local Minimum Calculus, Section 4. 1 6

Critical Numbers n n n Definition: “A critical number of a function f is a number c in the domain of f such that either f’(c) = 0 or f’(c) does not exist. ” Theorem: “If f has a local maximum or minimum at c, then c is a critical number of f. ” Translation: Any critical number has the potential of being a local maximum of minimum. Only at critical numbers can a local max or a local min exist. Calculus, Section 4. 1 7

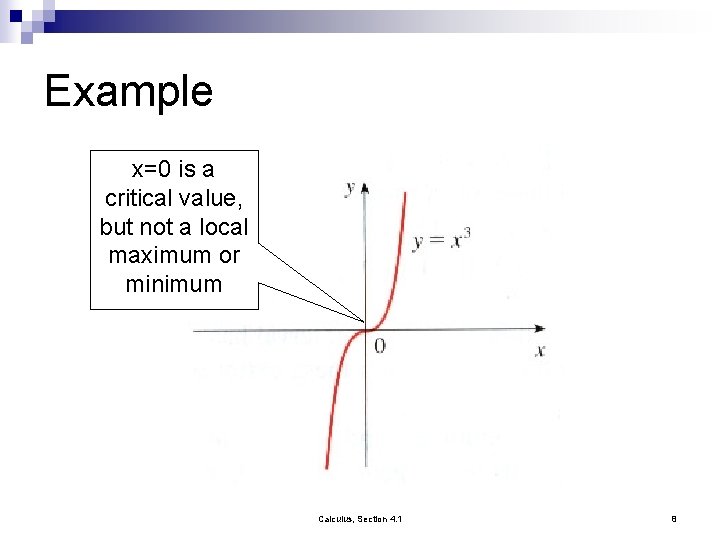
Example x=0 is a critical value, but not a local maximum or minimum Calculus, Section 4. 1 8

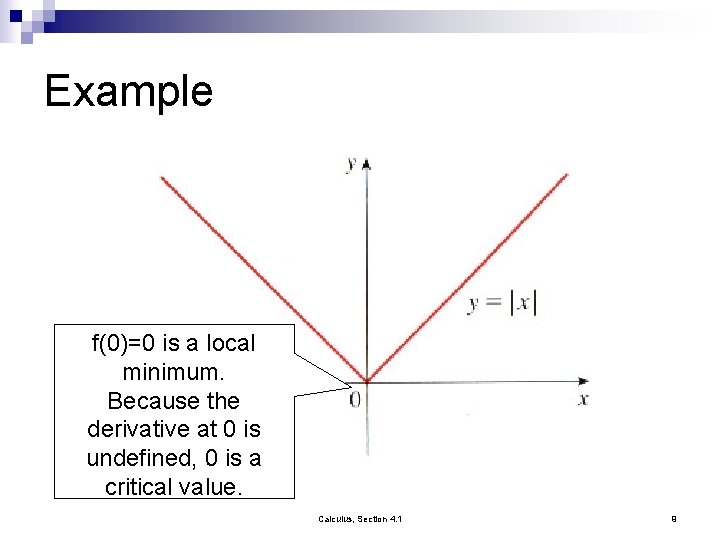
Example f(0)=0 is a local minimum. Because the derivative at 0 is undefined, 0 is a critical value. Calculus, Section 4. 1 9

Closed Interval Method To find the absolute maximum and minimum values of a continuous function f on a closed interval [a, b]: 1. Find the values of f at the critical numbers of f on (a, b) 2. Find the values of f at the endpoints of the interval. 3. The largest of the values for steps 1 & 2 is the absolute maximum value; the smallest of these values is the absolute minimum value. Calculus, Section 4. 1 10

Example Calculus, Section 4. 1 11

Example Absolute Minimum Absolute Maximum Calculus, Section 4. 1 12

Assignment n Section 4. 1, 15 -55, odd Calculus, Section 4. 1 13