5023 MAX Min Optimization AP Calculus OPEN INTERVALS

OPEN INTERVALS: Find the 1 st Derivative and the Critical Numbers • First Derivative

Example 1: Open - 1 st Derivative test VA=1 x=3, x=-1 Undefined at 1

# l a c iti CLOSED INTERVALS: EXTREME VALUE THEOREM: If f is continuous

CLOSED INTERVALS: Find the 1 st Derivative and the Critical Numbers • Closed Interval

Example : Closed Interval Test Co n sid ts. p d en er Absolute

OPTIMIZATION PROBLEMS • Used to determine Maximum and Minimum Values – i. e. »

METHOD: Set-Up Make a sketch. Assign variables to all given and to find quantities.

Relative Maximum and Minimum DEFN: Relative Extrema are the highest or lowest points in

Concavity and Max / Min SECOND DERIVATIVE TEST FOR MAX/MIN. If f is continuous

1 ILLUSTRATION : (with method) A landowner wishes to enclose a rectangular field

Example 2: Design an open box with the MAXIMUM VOLUME that has a square

Example 3: Find the dimensions of the largest rectangle that can be inscribed in

Example 4: min Find the point on closest to the point (0, -1). (0,

Example 5: A closed box with a square base is to have a volume

Example 6: Suppose that P(x), R(x), and C(x) are the profit, revenue, and cost

Last Update: 12/03/10 Assignment: DWK 4. 4

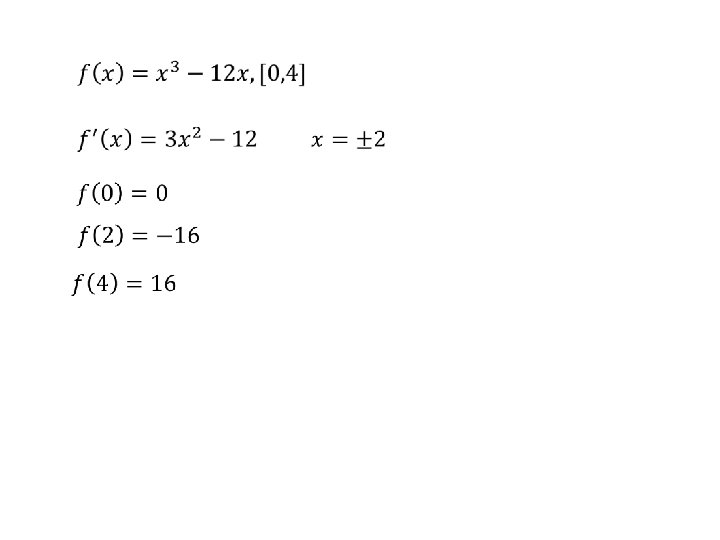
Slides: 23

Download presentation

5023 MAX - Min: Optimization AP Calculus

OPEN INTERVALS: Find the 1 st Derivative and the Critical Numbers • First Derivative Test for Max / Min – TEST POINTS on either side of the critical numbers – MAX: if the value changes from + to – – MIN: if the value changes from – to + • Second Derivative Test for Max / Min – FIND 2 nd Derivative – PLUG IN the critical number – MAX: if the value is negative – MIN: if the value is positive

Example 1: Open - 1 st Derivative test VA=1 x=3, x=-1 Undefined at 1 f’(x) + -1 -2 + 1 VA 0 3 2 4 max at -1 min at 3 and a VA at 1 why? Max of -2 at x=-1 because the first derivative goes from positive to negative at -1. Min of 6 at x=3 because 1 st derivative goes from negative to positive at 3. A VA at x=1 because 1 st derivative and the function are undefined at x=1

Example 2: Open - 2 nd Derivative Test

LHE p. 186

# l a c iti CLOSED INTERVALS: EXTREME VALUE THEOREM: If f is continuous on a closed interval [a, b], then f attains an absolute maximum f(c) and an absolute minimum f(d) at some points c and d in [a, b] Closed Interval Test Find the 1 st Derivative and the Critical Numbers Plug In the Critical Numbers and the End Points into the original equation MAX: if the Largest value MIN: if the Smallest value Cr local

CLOSED INTERVALS: Find the 1 st Derivative and the Critical Numbers • Closed Interval Test • Plug In the Critical Numbers and the End Points into the original equation • MAX: if the Largest value • MIN: if the Smallest value

Example : Closed Interval Test Co n sid ts. p d en er Absolute max absolute min

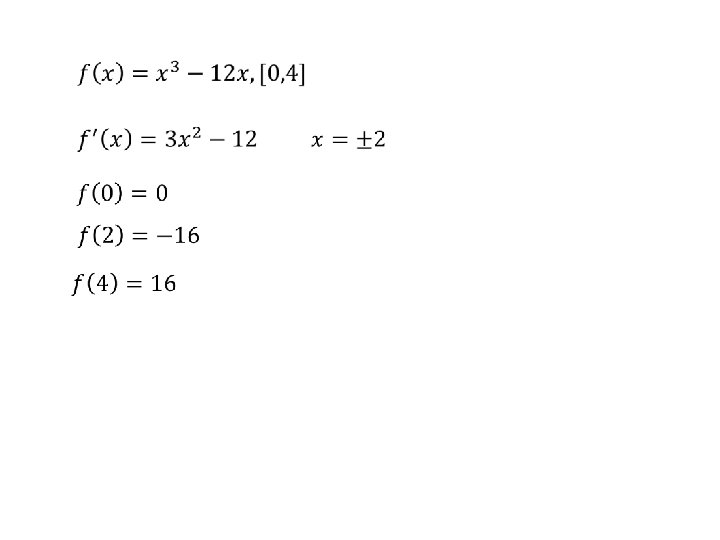
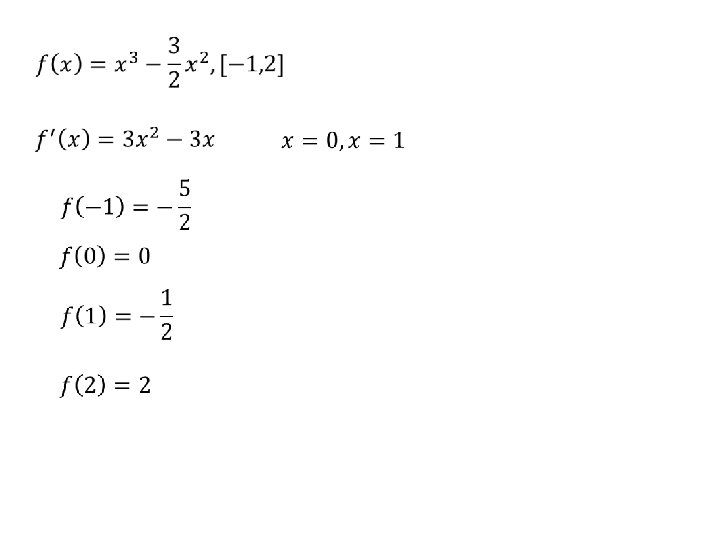
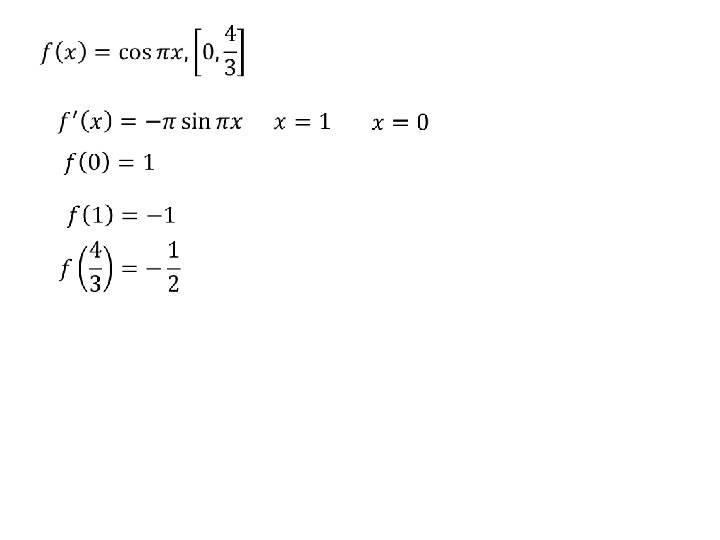
LHE p. 169 even numbers

OPTIMIZATION PROBLEMS • Used to determine Maximum and Minimum Values – i. e. » maximum profit, » least cost, » greatest strength, » least distance

METHOD: Set-Up Make a sketch. Assign variables to all given and to find quantities. Write a STATEMENT and PRIMARY (generic) equation to be maximized or minimized. PERSONALIZE the equation with the given information. Get the equation as a function of one variable. < This may involve a SECONDARY equation. > Find the Derivative and perform one the tests.

Relative Maximum and Minimum DEFN: Relative Extrema are the highest or lowest points in an interval. FIRST DERIVATIVE TEST FOR MAX/MIN. If f is continuous on [a, b] containing a critical number, c, and differentiable on (a, b) except possibly at c and if: Øf / (x) changes signs from (+) to (-) then f(c) is a relative Maximum. Øf / (x) changes signs from (-) to (+) then f(c) is a relative Minimum. Øf / (x) has no sign change then f(c) is neither. Note: c is the location. f Where is x (c) is the Max or Min value. What is y

Concavity and Max / Min SECOND DERIVATIVE TEST FOR MAX/MIN. If f is continuous on [a, b] and twice differentiable on (a, b) and if f (c) is a critical number, then Ø if f // (c) > 0 then f (x) is concave up and c is a minimum Ø if f // (c) < 0 then f (x) is concave down and c is a maximum Ø if f // (c) = 0 then the test is inconclusive.

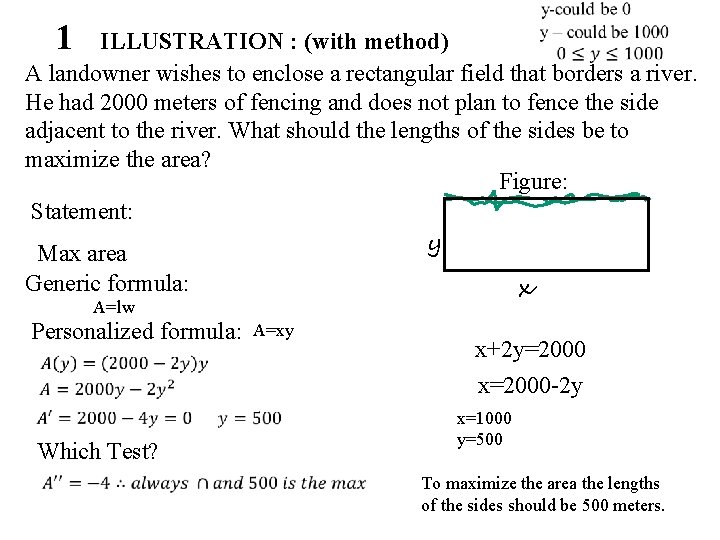
1 ILLUSTRATION : (with method) A landowner wishes to enclose a rectangular field that borders a river. He had 2000 meters of fencing and does not plan to fence the side adjacent to the river. What should the lengths of the sides be to maximize the area? Figure: Statement: y Max area x Generic formula: A=lw Personalized formula: Which Test? A=xy x+2 y=2000 x=2000 -2 y x=1000 y=500 To maximize the area the lengths of the sides should be 500 meters.

Example 2: Design an open box with the MAXIMUM VOLUME that has a square bottom and surface area of 108 square inches. y Statement: max volume of rect. prism Formula: Personalized Formula: x x

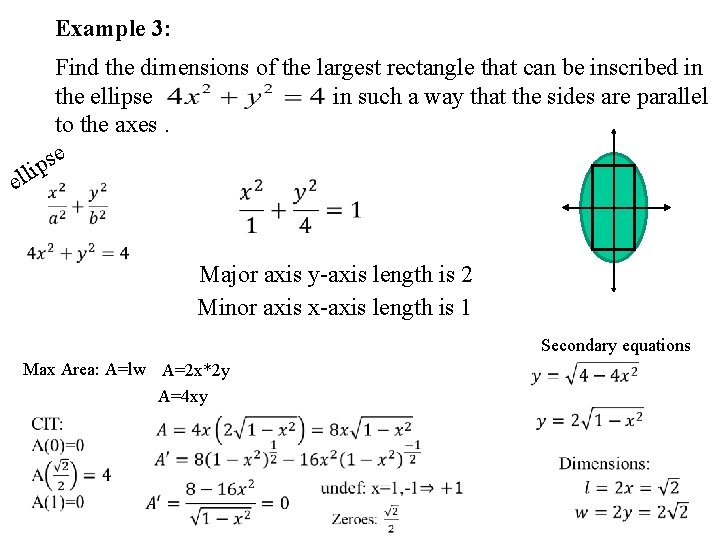
Example 3: Find the dimensions of the largest rectangle that can be inscribed in the ellipse in such a way that the sides are parallel to the axes. e s p i ell Major axis y-axis length is 2 Minor axis x-axis length is 1 Secondary equations Max Area: A=lw A=2 x*2 y A=4 xy

Example 4: min Find the point on closest to the point (0, -1). (0, -1)

Example 5: A closed box with a square base is to have a volume of 2000 in. 3. the material on the top and bottom will cost 3 cents per square inch and the material on the sides will cost 1 cent per square inch. Find the dimensions that will minimize the cost. Statement: minimize cost of material y Formula: x x

Example 6: Suppose that P(x), R(x), and C(x) are the profit, revenue, and cost functions, that P(x) = R(x) - C(x), and x represents thousand of units. Find the production level that maximizes the profit.

Last Update: 12/03/10 Assignment: DWK 4. 4