3 1 Maximum and Minimum Values Maximum and

3. 1 Maximum and Minimum Values

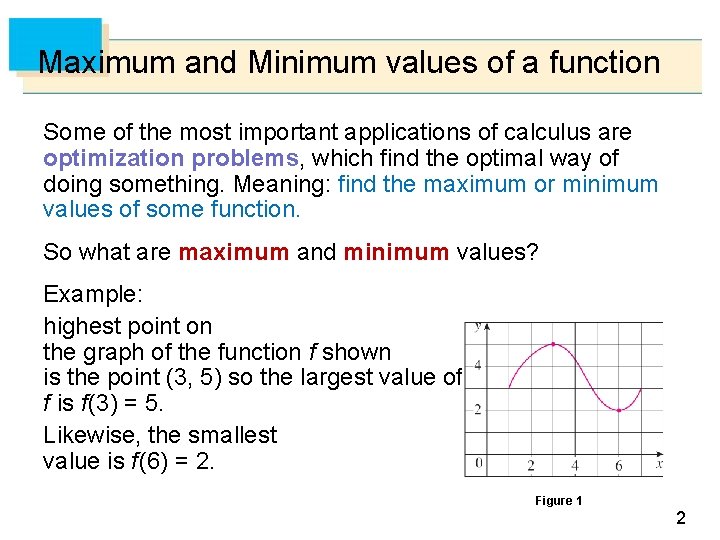
Maximum and Minimum values of a function Some of the most important applications of calculus are optimization problems, which find the optimal way of doing something. Meaning: find the maximum or minimum values of some function. So what are maximum and minimum values? Example: highest point on the graph of the function f shown is the point (3, 5) so the largest value of f is f (3) = 5. Likewise, the smallest value is f (6) = 2. Figure 1 2

Absolute Maximum and Minimum The maximum and minimum values of f are called extreme values of f. 3

Local Maximum and Minimum Something is true near c means that it is true on some open interval containing c. 4

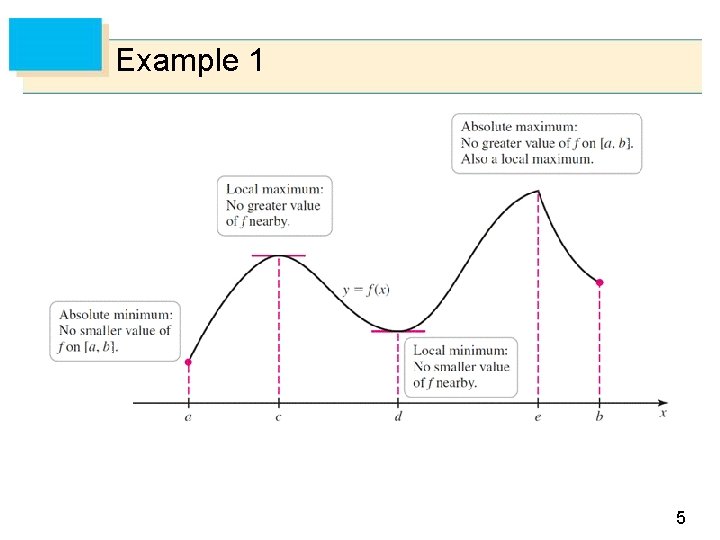
Example 1 5

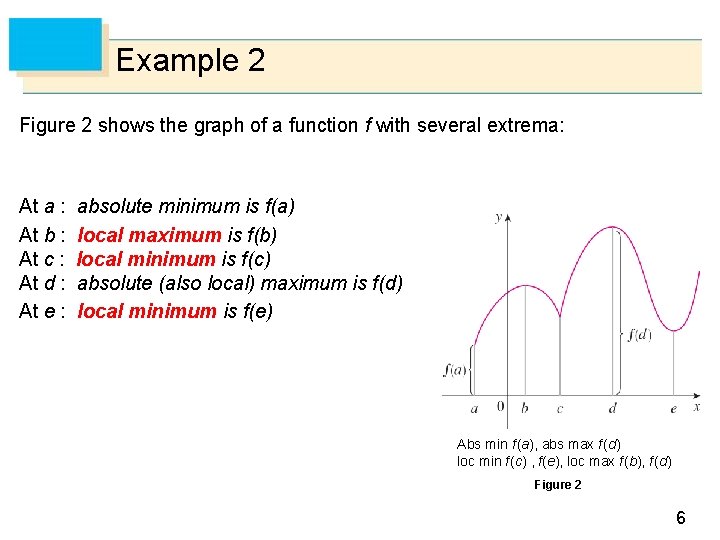
Example 2 Figure 2 shows the graph of a function f with several extrema: At a : At b : At c : At d : At e : absolute minimum is f(a) local maximum is f(b) local minimum is f(c) absolute (also local) maximum is f(d) local minimum is f(e) Abs min f (a), abs max f (d) loc min f (c) , f(e), loc max f (b), f (d) Figure 2 6

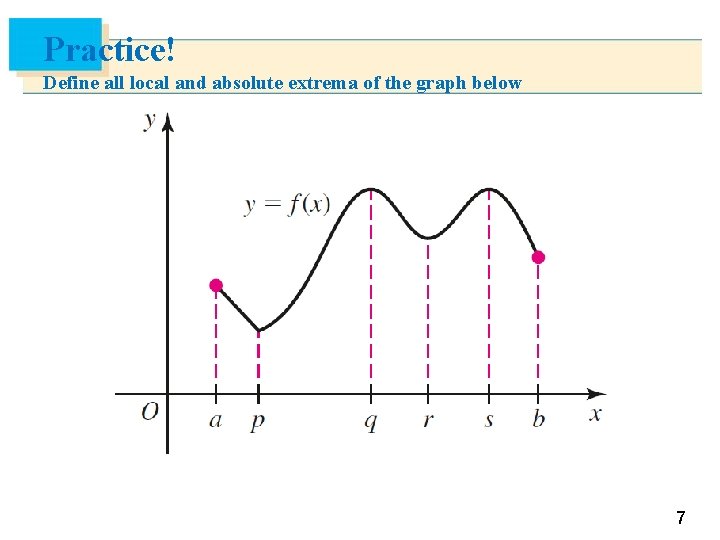
Practice! Define all local and absolute extrema of the graph below 7

Critical Point 8

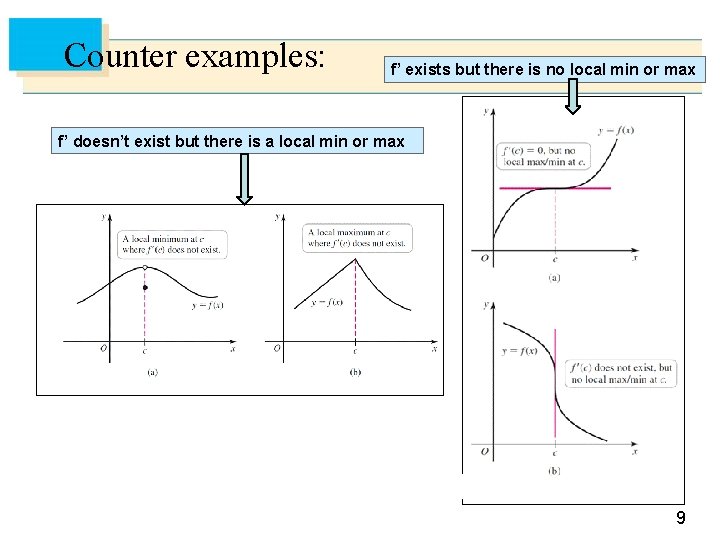
Counter examples: f’ exists but there is no local min or max f’ doesn’t exist but there is a local min or max 9

Extreme Value Theorem The following theorem gives conditions under which a function is guaranteed to have extreme values. 10

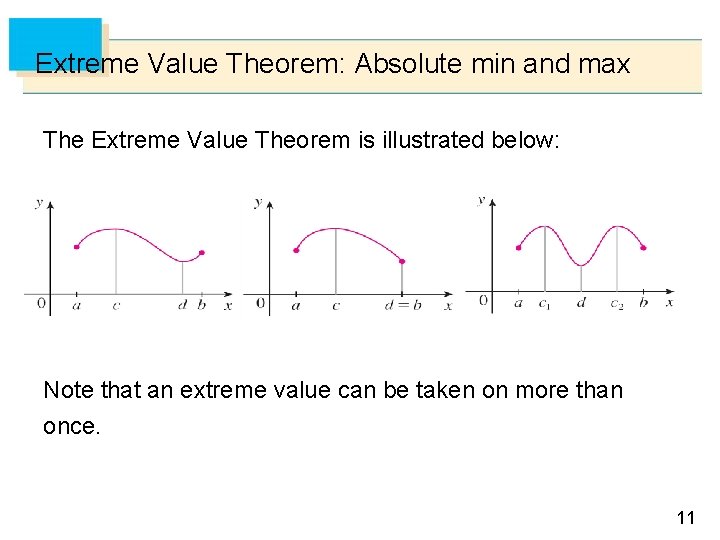
Extreme Value Theorem: Absolute min and max The Extreme Value Theorem is illustrated below: Figure 7 Note that an extreme value can be taken on more than once. 11

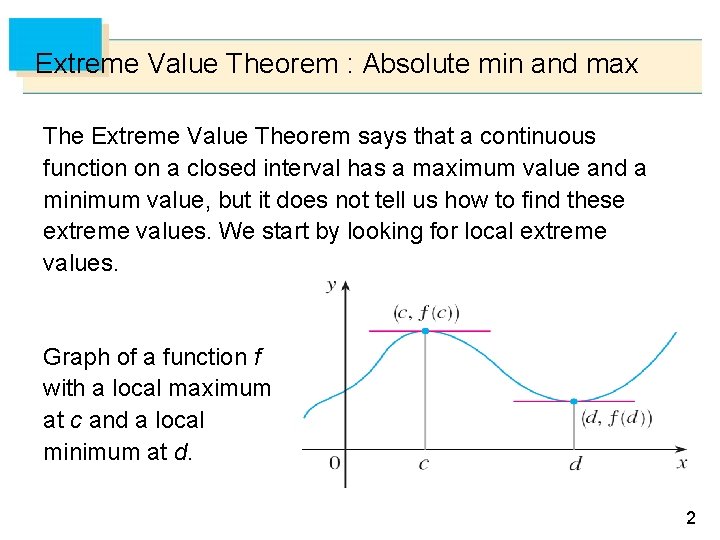
Extreme Value Theorem : Absolute min and max The Extreme Value Theorem says that a continuous function on a closed interval has a maximum value and a minimum value, but it does not tell us how to find these extreme values. We start by looking for local extreme values. Graph of a function f with a local maximum at c and a local minimum at d. Figure 10 12

Finding Absolute Maximum and Minimum of f: To find an absolute maximum or minimum of a continuous function on a closed interval, we note that either it is local or it occurs at an endpoint of the interval. Thus the following three-step procedure always works. 13

Practice Find the absolute values of the function and where they occur (worksheet 3. 1, # 5) 14

3. 2 The Mean Value Theorem 15

Rolle’s Theorem 16

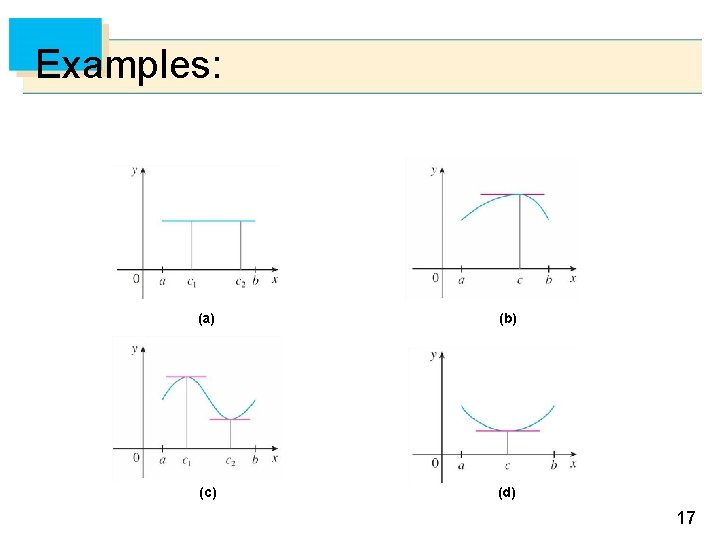
Examples: Figure 1 shows the graphs of four such functions. (a) (b) (c) (d) Figure 1 17

The Mean Value Theorem This theorem is an extension of Rolle’s Theorem 18

Example Show that f(x) satisfies the Mean Value Theorem on [a, b] f (x) = x 3 – x, Interval: a = 0, b = 2. Since f is a polynomial, it is continuous and differentiable for all x, so it is certainly continuous on [0, 2] and differentiable on (0, 2). Therefore, by the Mean Value Theorem, there is a number c in (0, 2) such that f (2) – f (0) = f (c)(2 – 0) 19

Example - proof f (2) = 6, f (0) = 0, and f (x) = 3 x 2 – 1, so this equation becomes: 6 = (3 c 2 – 1)2 = 6 c 2 – 2 which gives that is, c = But c must lie in (0, 2), so 20

The Mean Value Theorem can be used to establish some of the basic facts of differential calculus. 21