Optimization Problems Maximum Minimum values Most important in

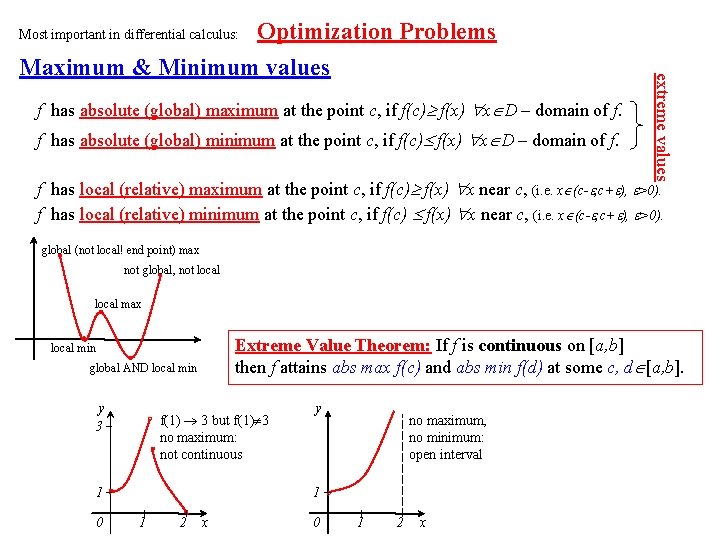
Optimization Problems Maximum & Minimum values Most important in differential calculus: f has absolute (global) minimum at the point c, if f(c) f(x) x D – domain of f. extreme values f has absolute (global) maximum at the point c, if f(c) f(x) x D – domain of f. f has local (relative) maximum at the point c, if f(c) f(x) x near c, (i. e. x (c-e, c+e), e>0). f has local (relative) minimum at the point c, if f(c) f(x) x near c, (i. e. x (c-e, c+e), e>0). global (not local! end point) max not global, not local max Extreme Value Theorem: If f is continuous on [a, b] then f attains abs max f(c) and abs min f(d) at some c, d [a, b]. local min global AND local min y 3 f(1) 3 but f(1) 3 no maximum: not continuous 1 0 y no maximum, no minimum: open interval 1 1 2 x 0 1 2 x

How to find local extreme values? y f (c)=0 Fermat’s Theorem: If f has a local maximum or minimum at c and if f (c) exists, then f (c)=0. f (d)=0 0 c d x But f (c)=0 doesn’t imply that c is local max or min! (e. g. f(x)=x 3, c=0). Existense of f (c) is important (e. g. f(x)=|x|, c=0). To find local extreme values: start from c, s. t. f (c)=0 or f (c) doesn’t exist. c – critical number of f. Fermat’s Theorem: If f has a local maximum or minimum at c then c is a critical number of f. local max/min, i. e. at critical number Absolute max/min of continuous function f on [a, b] = or at endpoint of the interval How to find absolute max/min? 1. find critical numbers in (a, b) and values of f there; 2. find values of f at endpoints; 3. abs max=max(step 1, step 2), abs min=min(step 1, step 2).

Proof of Fermat’s th. Assume f has a local max at c for all x near c, i. e. for any small h (both positive and negative), Divide by h: If h>0 Since f (c) exists, on the other hand, If h<0 Since f (c) exists, Therefore, If f has a local min at c, the proof is similar.

Rolle’s Theorem: Let f be 1. continuous on [a, b]; 2. differentiable on (a, b); 3. f(a)=f(b). c (a, b), s. t. f (c)=0 a c f (c)=0 f (d)=0 b a c b Case 1 a c f (c)=0 db a c Case 2 b Case 3 Ex. Show that f(x)=1+2 x+x 3+4 x 5 has exactly one real root. Mean Value Theorem: Let f be 1. continuous on [a, b]; 2. differentiable on (a, b). c (a, b), s. t. or f(a) f(b) f(a) a c b Th: If f (x)=0 x (a, b) then f is constant on (a, b). Corollary: If f (x)=g (x) x (a, b) then f -g is constant on (a, b). a c d b

Proof of Rolle’s th. Case 1. f(x) is constant Case 2. there exists By Extreme Value th. , f has an absolute max in [a, b]. Since f(a)=f(b) is not a maximum value, abs max is achieved at c (a, b), i. e. c – local max. f is differentiable at c by Fermat’s th. , Case 3. similar to Case 2: there exists By Extreme Value th. , f has an absolute min in [a, b]. Since f(a)=f(b) is not a minimum value, abs min is achieved at c (a, b), i. e. c – local min. f is differentiable at c by Fermat’s th. ,

If f (x)>0 on interval I, then f is increasing on I. If f (x)<0 on interval I, then f is decreasing on I. First derivative test. Let f be a continuous function, c – its critical number. 1. If f changes from positive to negative at c, then f has local max at c; 2. If f changes from negative to positive at c, then f has local min at c; 3. If f doesn’t change sign at c, then f has no local max or min at c. If f (x)>0 on interval I, then graph is concave upward on I. If f (x)<0 on interval I, then graph is concave downward on I. Concave upward Second derivative test. If f is continuous near c. 1. If f (c)=0 and f (c)>0, then f has local min at c; 2. If f (c)=0 and f (c)<0, then f has local max at c; Concave downward