Graph Algorithms Minimum Spanning Tree Spanning Tree A

Graph Algorithms Minimum Spanning Tree

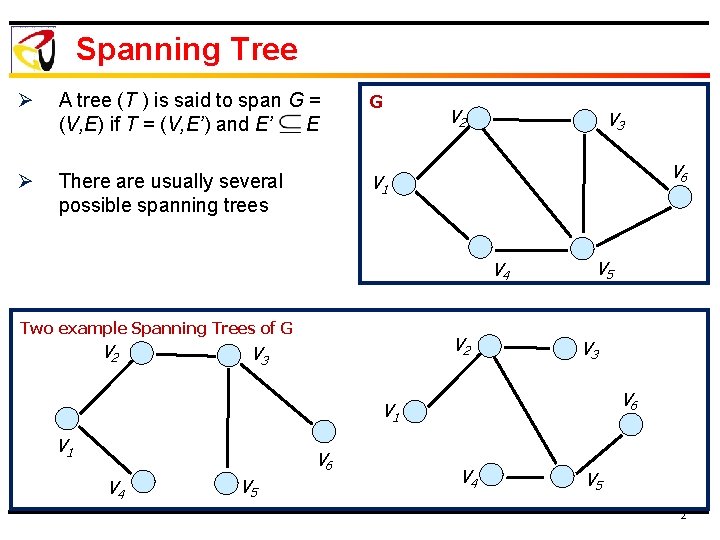
Spanning Tree Ø A tree (T ) is said to span G = (V, E) if T = (V, E’) and E’ E G Ø There are usually several possible spanning trees V 1 V 2 V 3 V 6 V 4 Two example Spanning Trees of G V 2 V 3 V 5 V 3 V 6 V 1 V 6 V 4 V 5 2

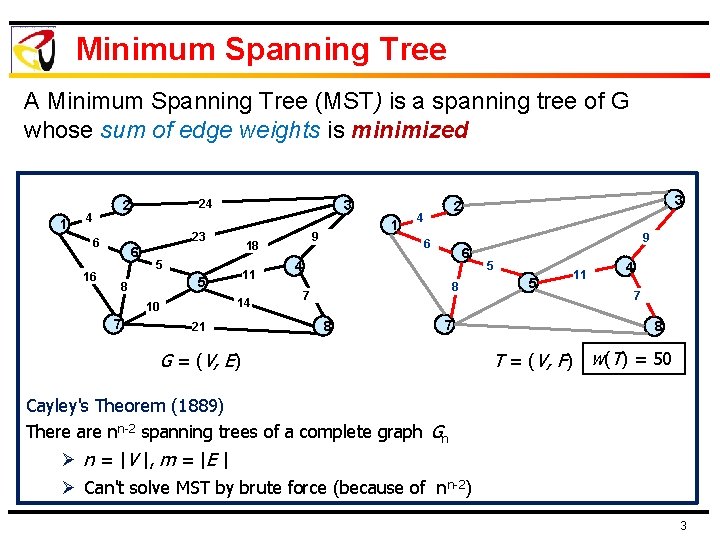
Minimum Spanning Tree A Minimum Spanning Tree (MST) is a spanning tree of G whose sum of edge weights is minimized 1 24 2 4 23 6 16 3 6 14 10 7 11 5 8 9 18 5 21 1 3 2 4 9 6 6 4 8 7 G = (V, E) 5 5 11 4 7 8 T = (V, F) w(T) = 50 Cayley's Theorem (1889) There are nn-2 spanning trees of a complete graph Gn Ø n = |V |, m = |E | Ø Can't solve MST by brute force (because of nn-2) 3

Constructing a Minimum Spanning Tree Ø Properties of an MST Ø |V|-1 Edges Ø No Cycles Ø Might not be Unique Ø Constructing an MST Ø Defined as a set of Edges A Ø Initially A has no Edges Ø Iteratively add SAFE Edges to A until MST is constructed 4

Safe Edges l 5

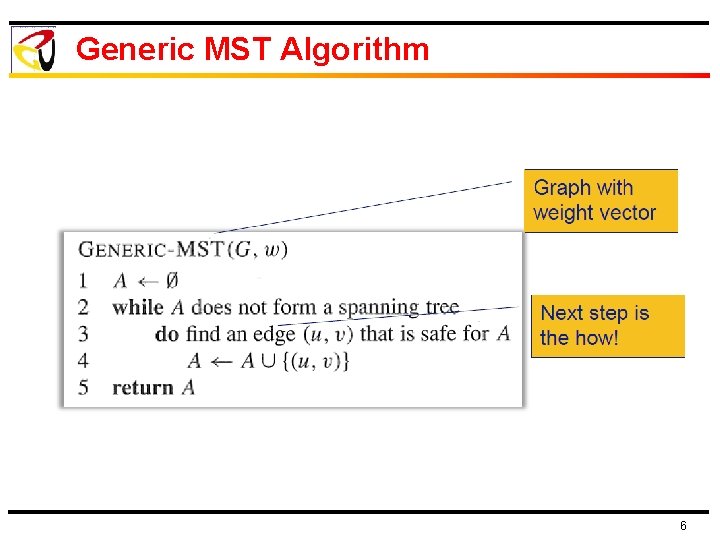
Generic MST Algorithm 6

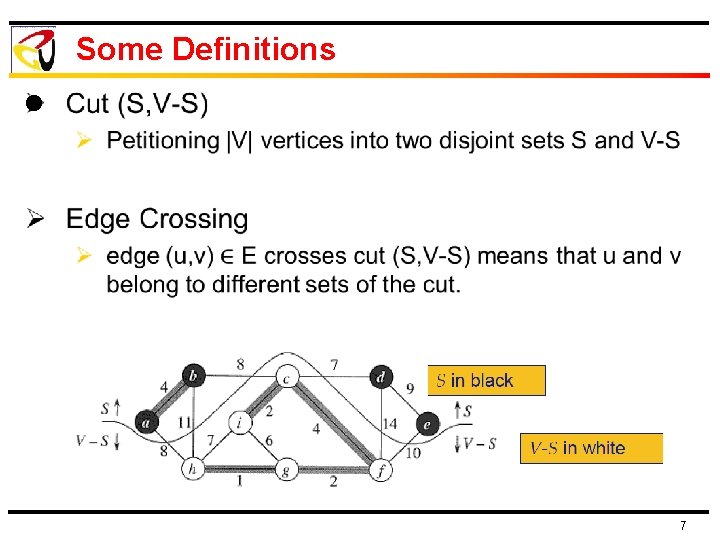
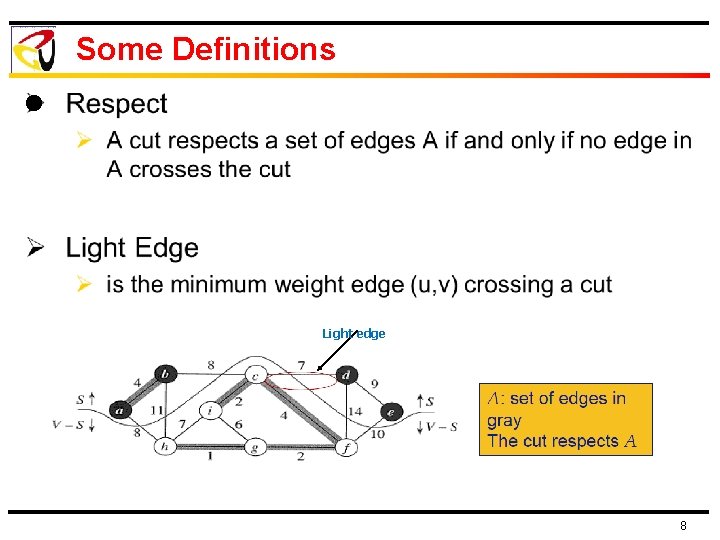
Some Definitions l 7

Some Definitions l Light edge 8

Theorem Let A be a subset of some MST, (S, V-S) be a cut that respects A, and (u, v) be a light edge crossing (S, V-S) Then (u, v) is safe for A Edge No Loops Light Satisfies the minimum cost objective of MST 9

Two Algorithms to be Considered Greedy Algorithms Ø Kruskal’s Algorithm, Ø Prim’s Algorithm 10

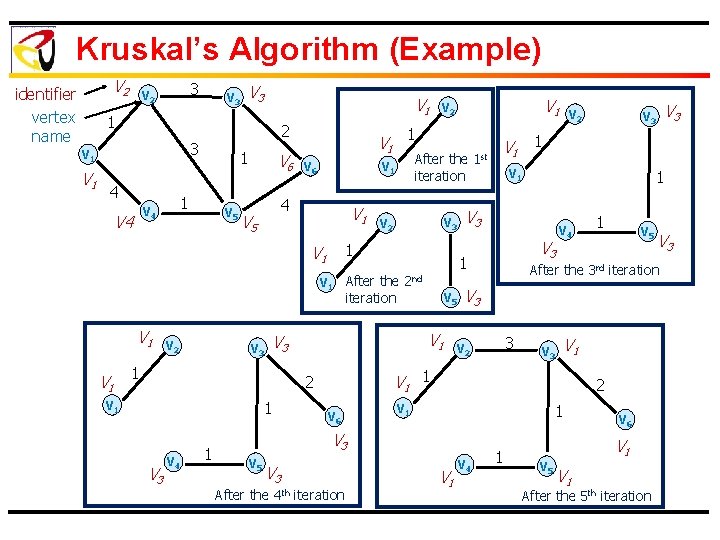
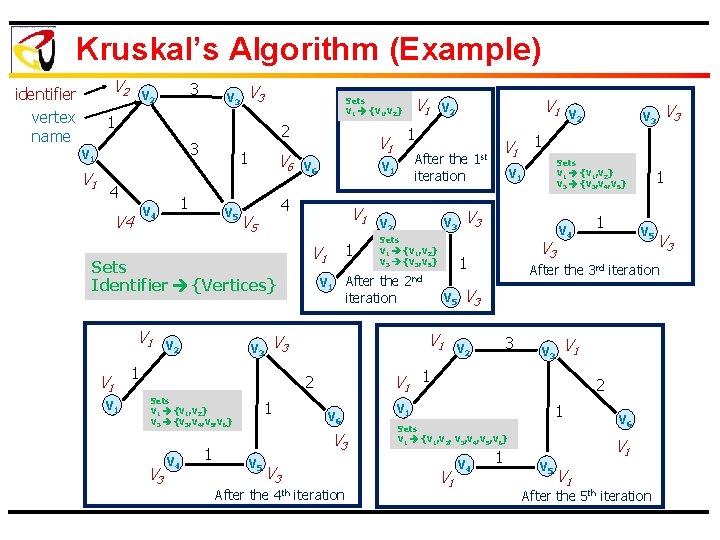
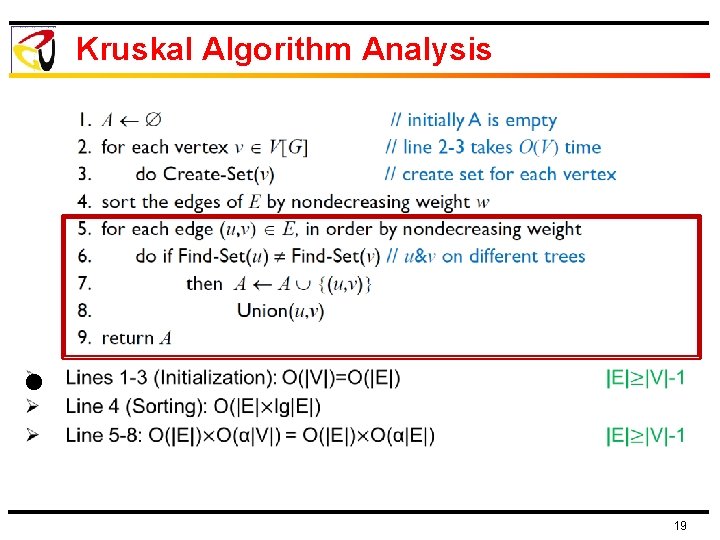
MST Computation Kruskal’s Algorithm Ø Sort edges in increasing order of weight Ø Select edges e E in sequence from the sorted list Ø Continue to add the edge e to A such that it does not form a cycle Ø Edges are added to A until |A| = |V|-1 11

Kruskal Algorithm Ø Ø Ø Create-Set(u): Creates a set containing u with a unique set identifier Find-Set(u): Returns the identifier of the set that contains u Union(u, v): Merges the sets containing u and v. All elements of the merged set will have the same identifier 12

Kruskal’s Algorithm (Example) V 2 identifier vertex name 3 V 2 V 3 V 1 1 3 V 1 2 4 1 V 5 V 6 V 1 V 1 V 2 V 3 After the iteration V 3 V 4 1 V 5 V 1 V 6 V 3 V 1 1 V 3 V 4 After the 4 th iteration 1 V 5 V 3 3 V 2 V 3 V 1 1 V 4 V 3 After the 3 rd iteration 2 V 1 V 3 V 1 1 V 3 V 5 V 2 V 1 1 2 1 1 st 1 2 nd V 3 1 V 3 V 2 1 V 1 After the iteration V 1 4 V 5 1 V 6 V 1 V 2 1 V 6 V 1 V 5 V 1 After the 5 th iteration

Kruskal’s Algorithm (Example) V 2 identifier vertex name 3 V 2 V 3 1 V 1 2 3 V 1 4 V 4 1 1 V 4 V 5 V 6 V 1 V 2 V 6 V 5 V 3 1 V 1 V 3 V 4 1 1 st V 1 1 V 5 V 2 V 3 V 4 V 3 After the 4 th iteration 1 1 V 5 V 3 3 V 2 V 3 V 1 2 V 1 1 Sets V 1 {V 1, V 2, V 3, V 4, V 5, V 6} V 1 V 4 V 3 After the 3 rd iteration V 1 1 V 6 V 3 Sets V 1 {V 1, V 2} V 3 {V 3, V 4, V 5} V 1 1 2 nd V 1 V 3 V 5 Sets V 1 {V 1, V 2} V 3 {V 3, V 5} After the iteration 2 1 V 3 V 2 V 3 1 Sets V 1 {V 1, V 2} V 3 {V 3, V 4, V 5, V 6} After the iteration V 1 V 1 V 2 1 V 1 4 Sets Identifier {Vertices} V 1 Sets V 1 {V 1, V 2} 1 V 6 V 1 V 5 V 1 After the 5 th iteration

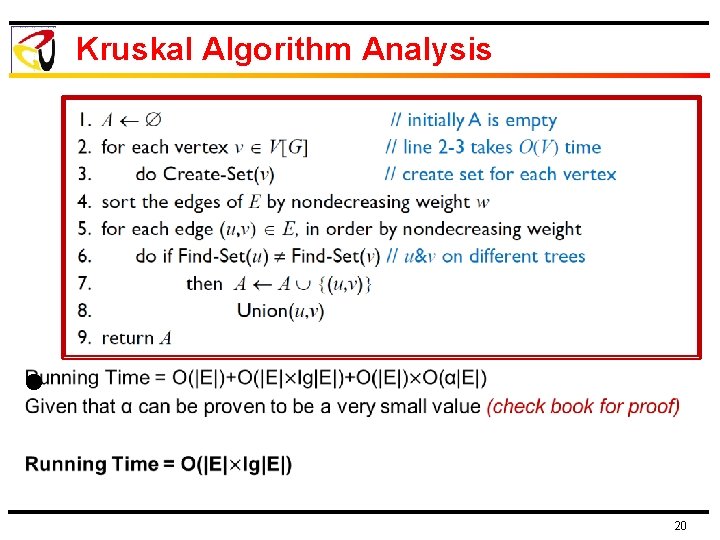
Kruskal Algorithm Analysis Ø Lines 1 -3 (Initialization): O(V) 15

Kruskal Algorithm Analysis l 16

Kruskal Algorithm Analysis l 17

Kruskal Algorithm Analysis l 18

Kruskal Algorithm Analysis l 19

Kruskal Algorithm Analysis l 20

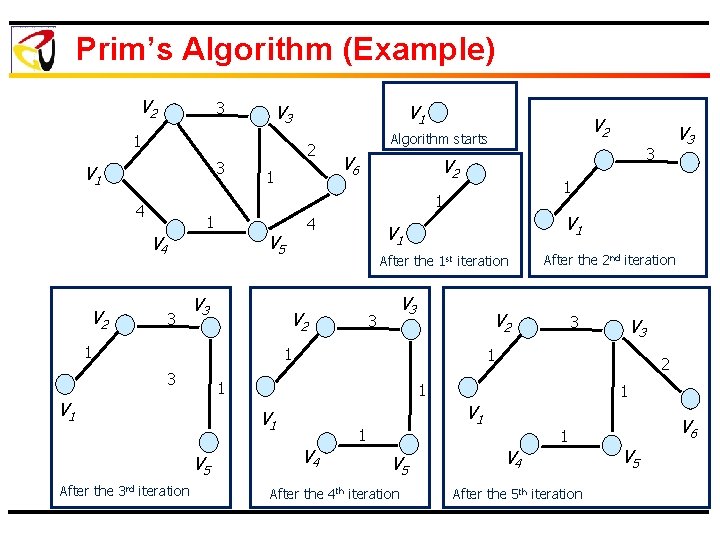
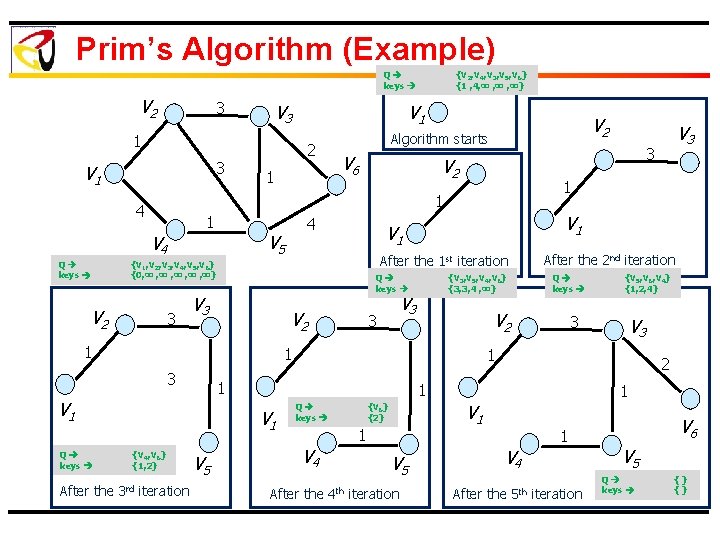
MST Computation Prim’s Algorithm: Ø Select an arbitrary node as the initial tree (T) Ø Augment T in an iterative fashion by adding the outgoing edge (u, v), (i. e. , u T and v G-T ) with minimum cost (i. e. , light edge) Ø The algorithm stops after |V| - 1 iterations 21

Prim’s Algorithm l key[u]: the cost to enter spanning tree set π[u]: the vertex through which u can be added to the spanning tree set 22

Prim’s Algorithm l Make cost of the root = 0 23

Prim’s Algorithm l Add all vertices to a queue Q such that r (root) is at the head of the list 24

Prim’s Algorithm l Extract the vertex at the head of the queue 25

Prim’s Algorithm l For each adjacent vertex check if it is has been added or not to the spanning tree (still in Queue? ) If it has not been added to the spanning tree, update the cost of entering the spanning tree set 26

Prim’s Algorithm l Update position of v in Q such that it remains sorted 27

Prim’s Algorithm (Example) V 2 3 V 3 1 3 V 1 2 1 V 2 Algorithm starts V 6 1 V 4 3 4 V 5 V 3 1 1 V 1 After the 1 st iteration V 2 3 V 3 After the 3 rd iteration V 3 2 1 V 5 3 1 1 V 1 After the 2 nd iteration V 2 1 3 V 4 1 V 1 1 V 5 After the 4 th iteration V 3 3 V 2 1 4 V 2 V 1 V 4 1 After the 5 th iteration V 6 V 5

Prim’s Algorithm (Example) Q keys V 2 3 V 3 1 3 V 1 1 V 4 2 1 3 1 V 1 3 {V 3, V 5, V 4, V 6} {3, 3, 4 , ∞} V 3 iteration V 5 3 {V 5, V 6, V 4} {1, 2, 4} V 3 1 1 2 1 V 1 {V 4, V 6} {1, 2} Q keys V 2 1 V 1 After the 2 nd iteration After the 1 st iteration V 2 Q keys 1 V 4 After the V 5 4 th 1 V 1 {V 6} {2} iteration V 3 3 V 2 Q keys V 3 3 After the V 6 4 V 5 1 3 rd V 2 Algorithm starts {V 1, V 2, V 3, V 4, V 5, V 6} {0, ∞ , ∞ , ∞} V 2 Q keys V 1 1 4 Q keys {V 2, V 4, V 3, V 5, V 6} {1 , 4, ∞ , ∞} V 4 After the 5 th 1 iteration V 6 V 5 Q keys {} {}

Analysis of Prim’s Algorithm l O(|V|) 30

Analysis of Prim’s Algorithm l Loop O(|V|) 31

Analysis of Prim’s Algorithm l O(|V|) Loop O(|V|) O(1) Total 2|E| Edges 32

Analysis of Prim’s Algorithm l Loop O(|V|) O(1) Total 2|E| Edges O(1) O(lg(|V|)) Binary search 33

Analysis of Prim’s Algorithm l Loop O(|V|) O(1) Total 2|E| Edges O(1) O(lg(|V|)) 34