Selection Trees Winner trees Loser Trees Winner Trees

Selection Trees Winner trees. Loser Trees.

Winner Trees Complete binary tree with n external nodes and n - 1 internal nodes. External nodes represent tournament players. Each internal node represents a match played between its two children; the winner of the match is stored at the internal node. Root has overall winner.

Tournament tree (Bracket)

Winner Tree For 16 Players player match node

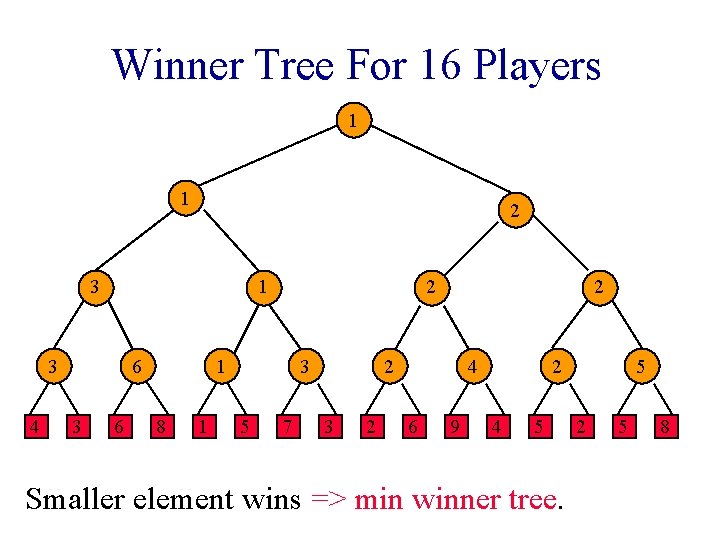
Winner Tree For 16 Players 1 1 2 3 1 3 4 6 3 6 2 1 8 1 3 5 7 2 2 3 2 4 6 9 2 4 5 Smaller element wins => min winner tree. 5 2 5 8

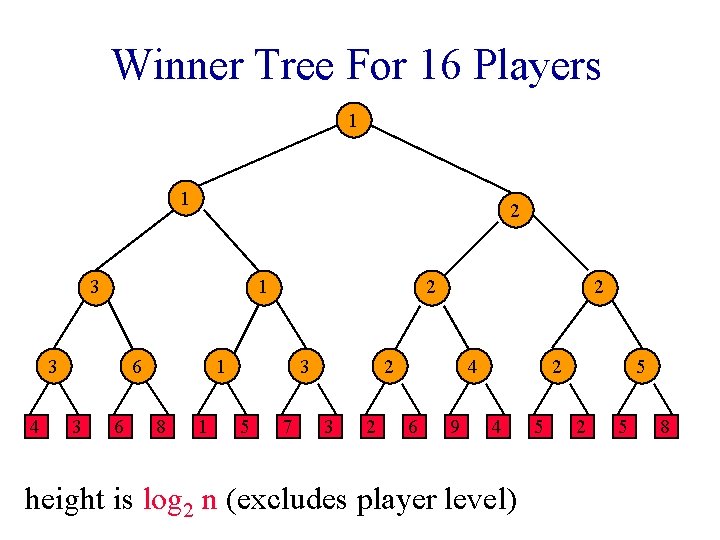
Winner Tree For 16 Players 1 1 2 3 1 3 4 6 3 6 2 1 8 1 3 5 7 2 2 3 2 4 6 9 2 4 height is log 2 n (excludes player level) 5 5 2 5 8

Complexity Of Initialize • O(1) time to play match at each match node. • n - 1 match nodes. • O(n) time to initialize n player winner tree.

Applications Sorting. Insert elements to be sorted into a winner tree. Repeatedly extract the winner and replace by a large value.

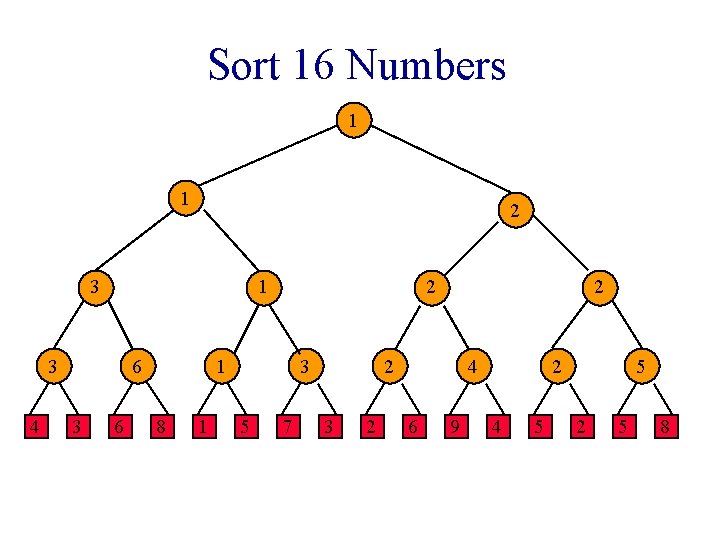
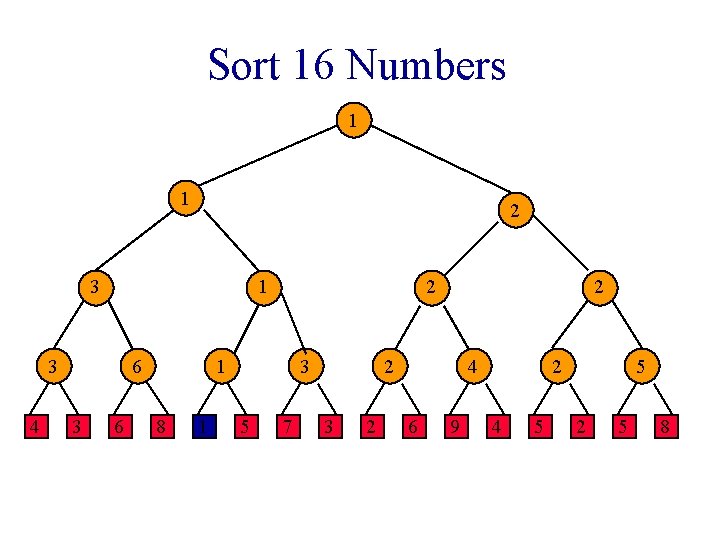
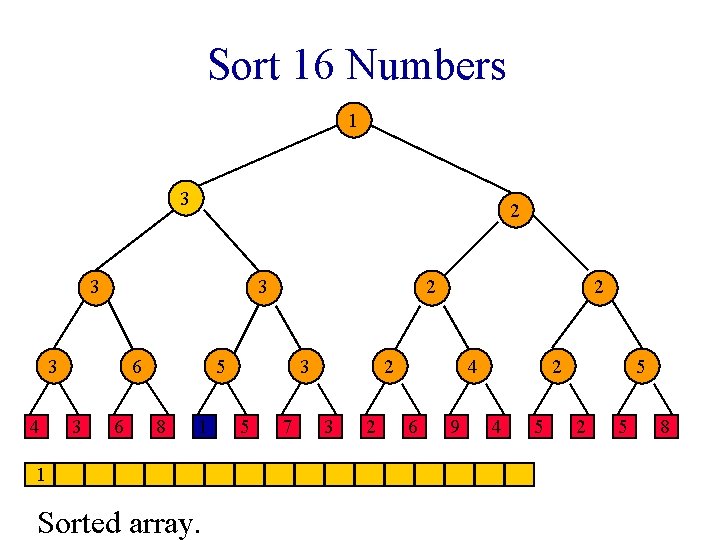
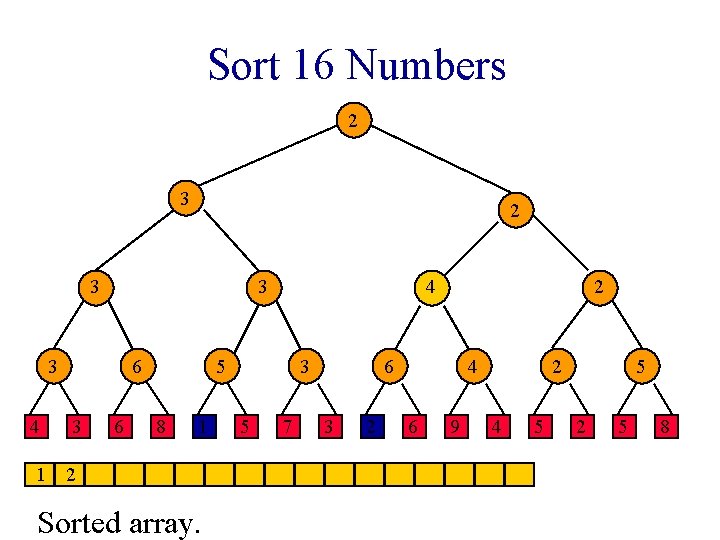
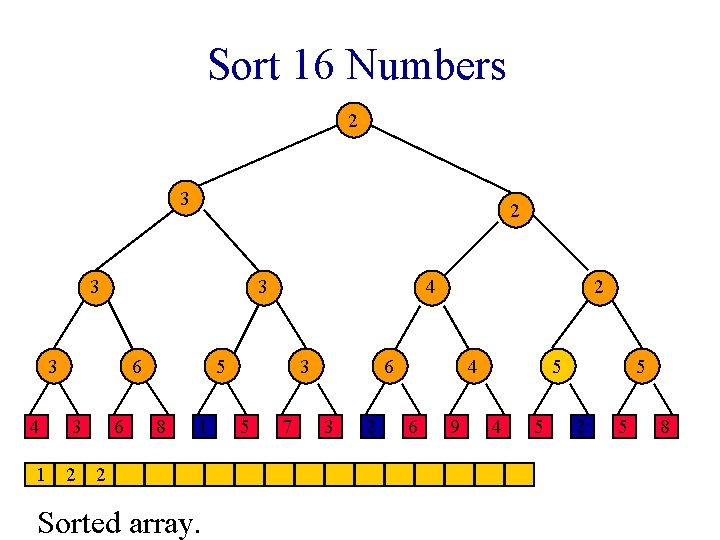
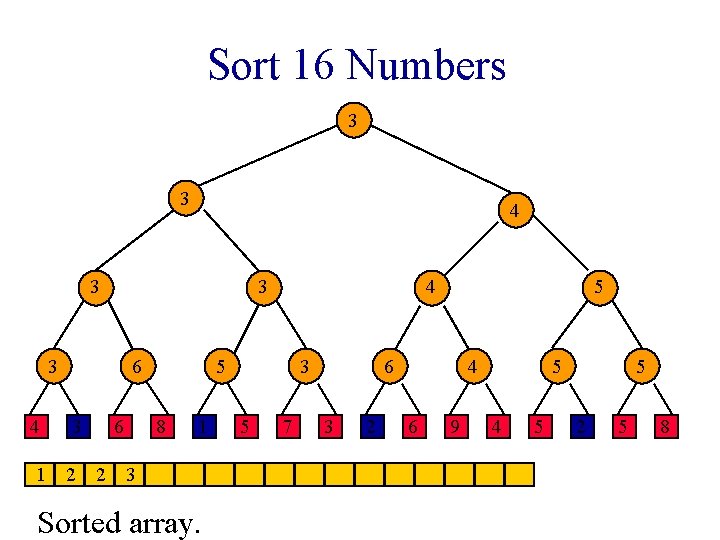
Sort 16 Numbers 1 1 2 3 1 3 4 6 3 6 2 1 8 1 3 5 7 2 2 3 2 4 6 9 2 4 5 5 2 5 8

Sort 16 Numbers 1 1 2 3 1 3 4 6 3 6 2 1 8 1 3 5 7 2 2 3 2 4 6 9 2 4 5 5 2 5 8

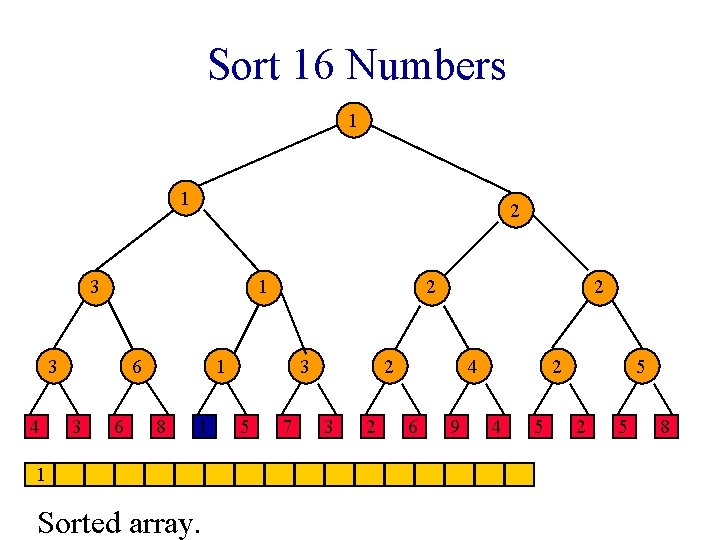
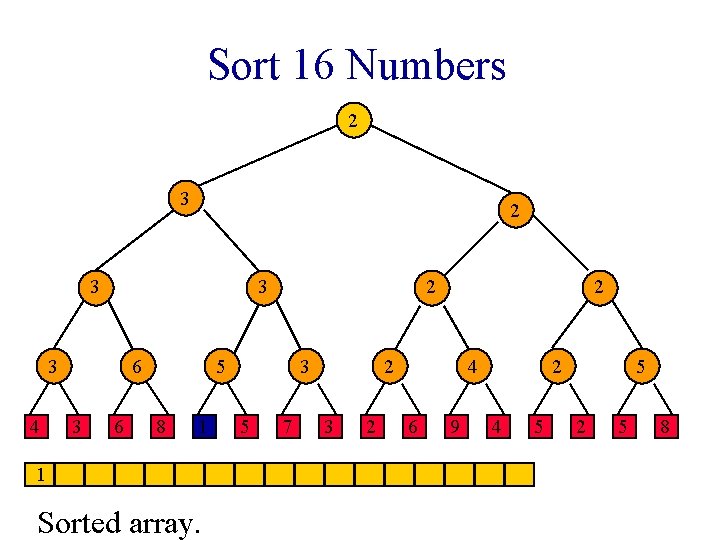
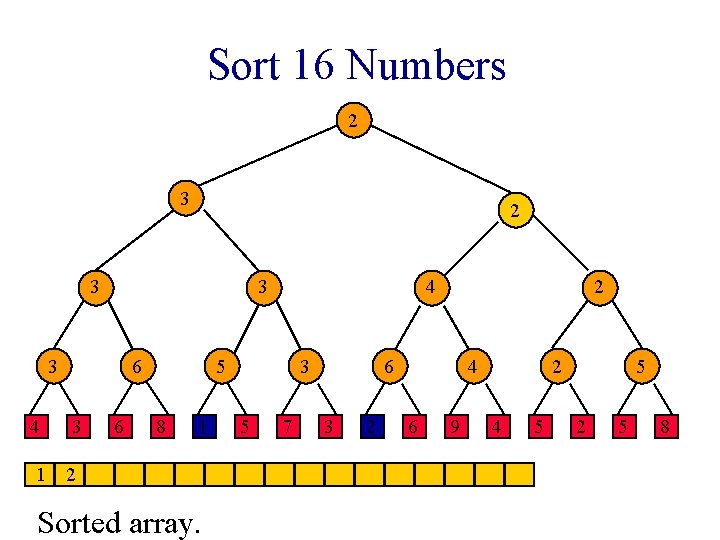
Winner Tree Sorting Method 1. Put elements to be sorted into a min winner tree. 2. Remove the winner and replace its value with a large value (e. g. , ∞). 3. replay the matches. 4. If not done, go to step 2.

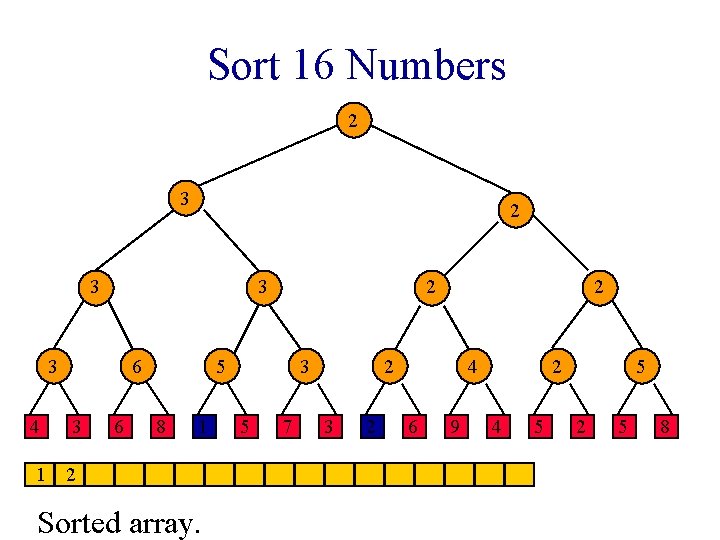
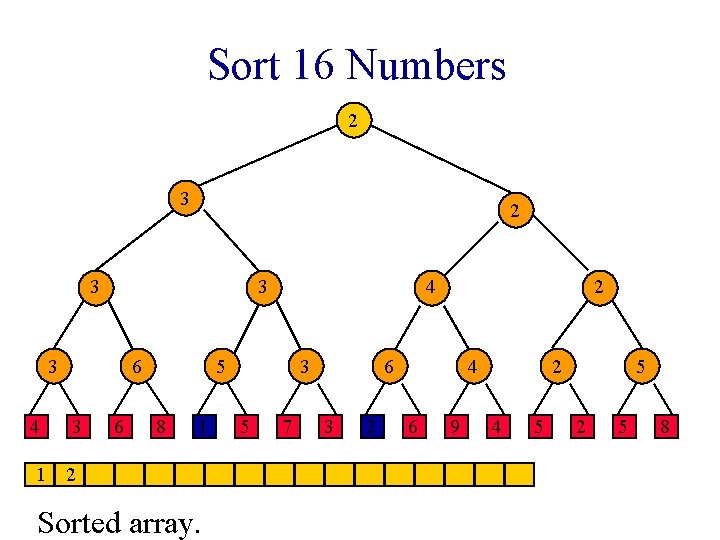
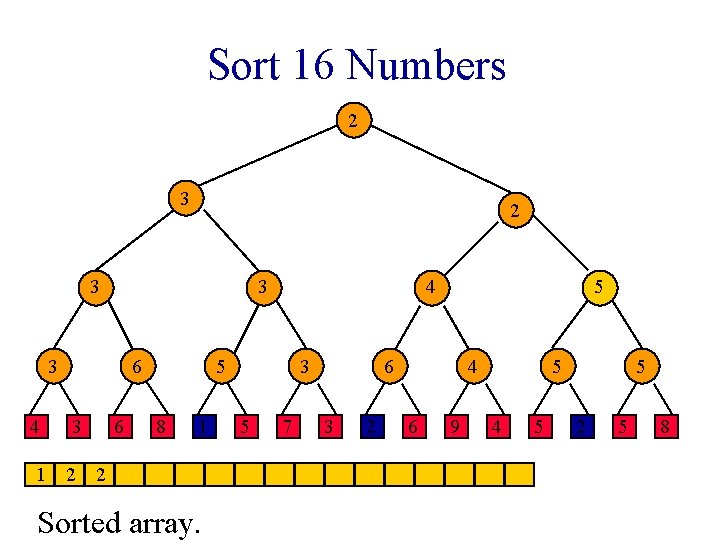
Sort 16 Numbers 1 1 2 3 1 3 4 6 3 6 2 1 8 1 1 Sorted array. 3 5 7 2 2 3 2 4 6 9 2 4 5 5 2 5 8

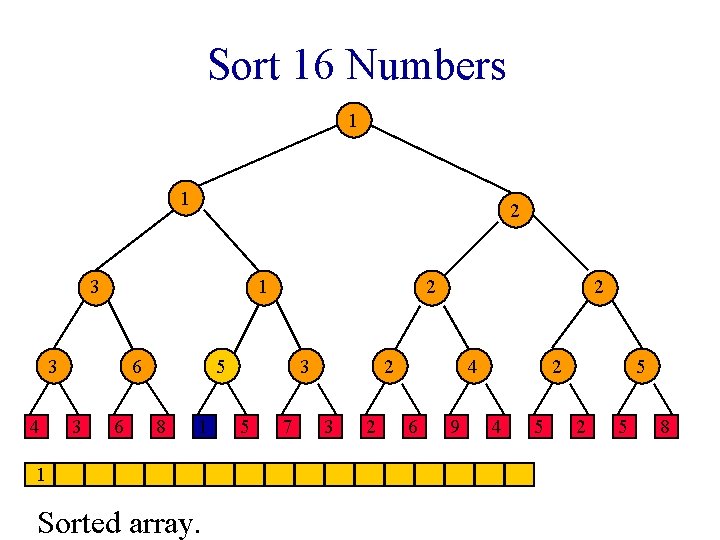
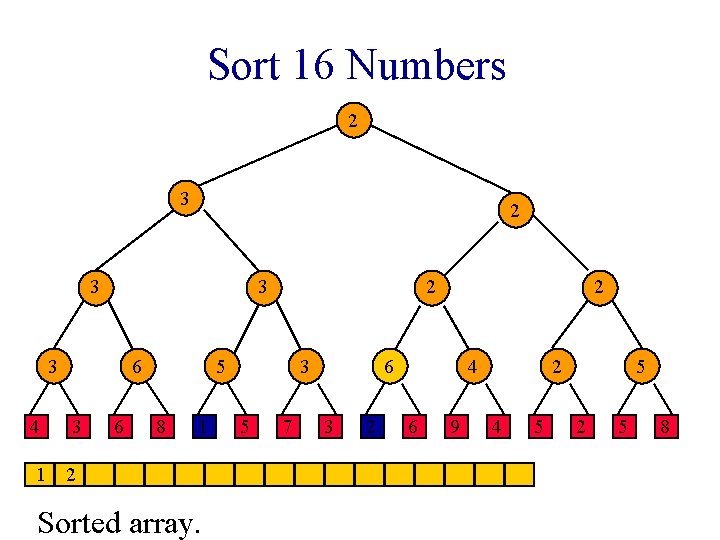
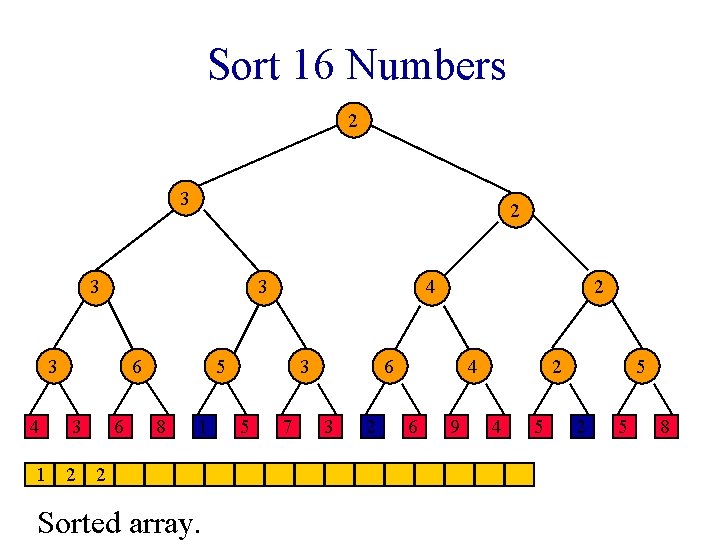
Sort 16 Numbers 1 1 2 3 1 3 4 6 3 6 2 5 8 1 1 Sorted array. 3 5 7 2 2 3 2 4 6 9 2 4 5 5 2 5 8

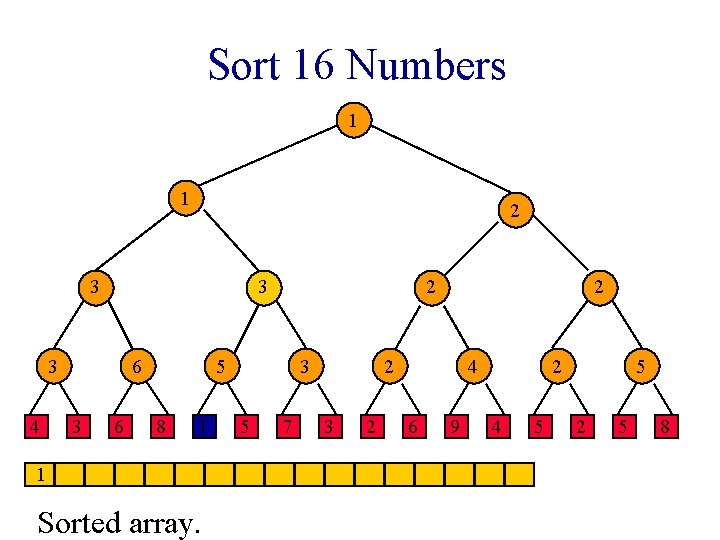
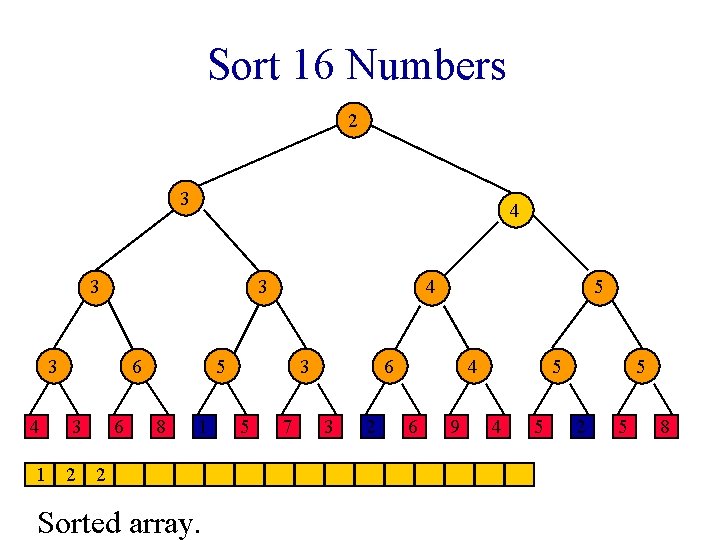
Sort 16 Numbers 1 1 2 3 3 3 4 6 3 6 2 5 8 1 1 Sorted array. 3 5 7 2 2 3 2 4 6 9 2 4 5 5 2 5 8

Sort 16 Numbers 1 3 2 3 3 3 4 6 3 6 2 5 8 1 1 Sorted array. 3 5 7 2 2 3 2 4 6 9 2 4 5 5 2 5 8

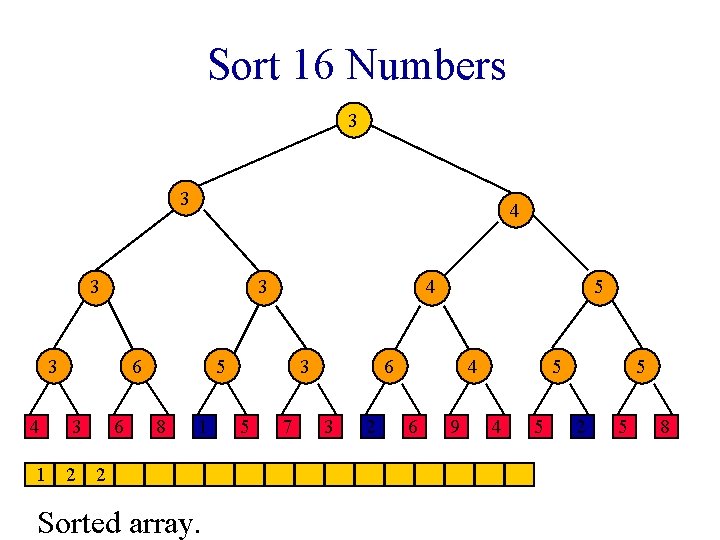
Sort 16 Numbers 2 3 3 3 4 6 3 6 2 5 8 1 1 Sorted array. 3 5 7 2 2 3 2 4 6 9 2 4 5 5 2 5 8

Sort 16 Numbers 2 3 3 3 6 4 3 1 2 6 2 5 8 1 Sorted array. 3 5 7 2 2 3 2 4 6 9 2 4 5 5 2 5 8

Sort 16 Numbers 2 3 3 3 6 4 3 1 2 6 2 5 8 1 Sorted array. 3 5 7 2 6 3 2 4 6 9 2 4 5 5 2 5 8

Sort 16 Numbers 2 3 3 3 6 4 3 1 2 6 4 5 8 1 Sorted array. 3 5 7 2 6 3 2 4 6 9 2 4 5 5 2 5 8

Sort 16 Numbers 2 3 3 3 6 4 3 1 2 6 4 5 8 1 Sorted array. 3 5 7 2 6 3 2 4 6 9 2 4 5 5 2 5 8

Sort 16 Numbers 2 3 3 3 6 4 3 1 2 6 4 5 8 1 Sorted array. 3 5 7 2 6 3 2 4 6 9 2 4 5 5 2 5 8

Sort 16 Numbers 2 3 3 3 6 4 3 1 2 6 4 5 8 1 2 Sorted array. 3 5 7 2 6 3 2 4 6 9 2 4 5 5 2 5 8

Sort 16 Numbers 2 3 3 3 6 4 3 1 2 6 4 5 8 1 2 Sorted array. 3 5 7 2 6 3 2 4 6 9 5 4 5 5 2 5 8

Sort 16 Numbers 2 3 3 3 6 4 3 1 2 6 4 5 8 1 2 Sorted array. 3 5 7 5 6 3 2 4 6 9 5 4 5 5 2 5 8

Sort 16 Numbers 2 3 4 3 3 3 6 4 3 1 2 6 4 5 8 1 2 Sorted array. 3 5 7 5 6 3 2 4 6 9 5 4 5 5 2 5 8

Sort 16 Numbers 3 3 4 3 3 3 6 4 3 1 2 6 4 5 8 1 2 Sorted array. 3 5 7 5 6 3 2 4 6 9 5 4 5 5 2 5 8

Sort 16 Numbers 3 3 4 3 3 3 6 4 3 1 2 6 2 4 5 8 1 3 Sorted array. 3 5 7 5 6 3 2 4 6 9 5 4 5 5 2 5 8

Time To Sort • Initialize winner tree. § O(n) time • Remove winner and replay. § O(log n) time • Remove winner and replay n times. § O(n log n) time • Total sort time is O(n log n). • Actually Theta(n log n).

Winner Tree Operations • Initialize § O(n) time • Get winner § O(1) time • Remove/replace winner and replay § O(log n) time § more precisely Theta(log n)

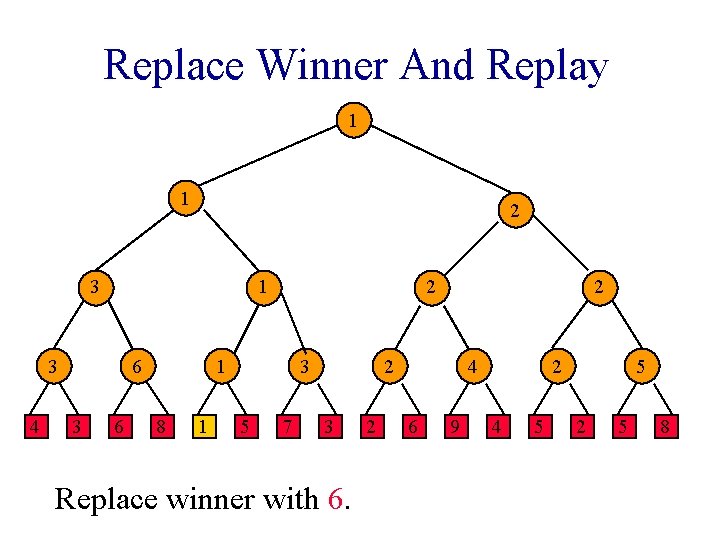
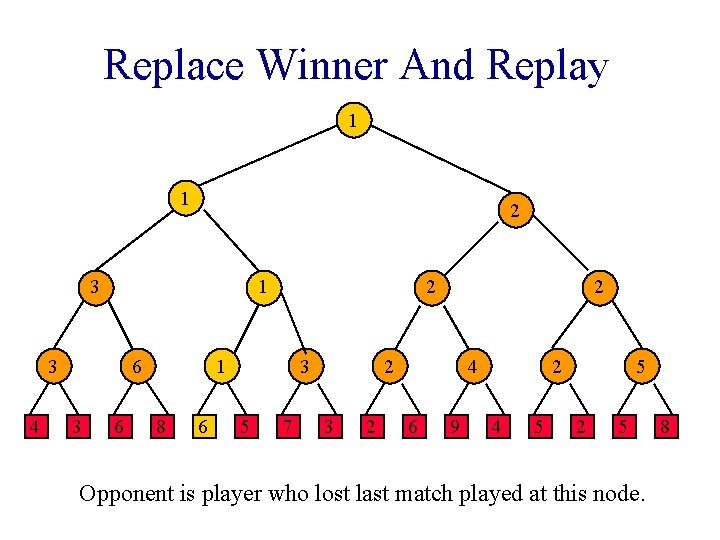
Replace Winner And Replay 1 1 2 3 1 3 4 6 3 6 2 1 8 1 3 5 7 2 2 3 Replace winner with 6. 2 4 6 9 2 4 5 5 2 5 8

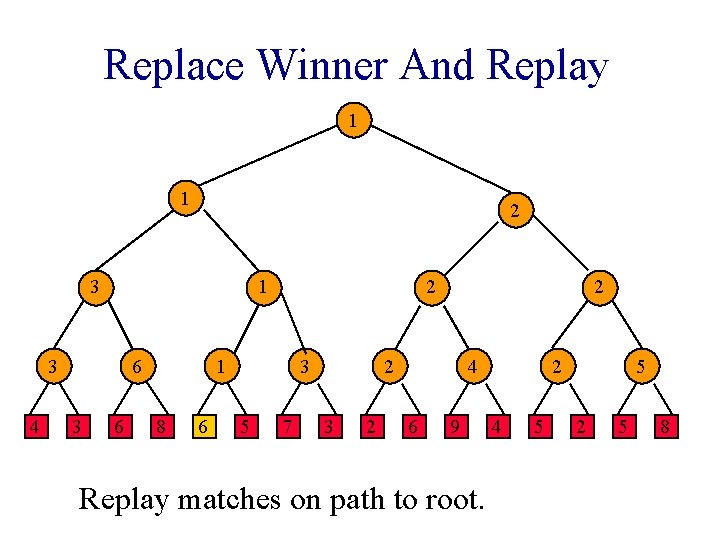
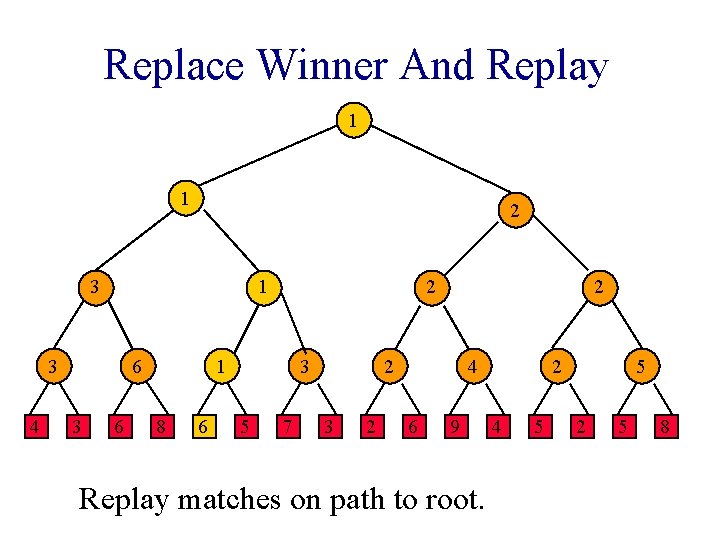
Replace Winner And Replay 1 1 2 3 1 3 4 6 3 6 2 1 8 6 3 5 7 2 2 3 2 4 6 9 Replay matches on path to root. 2 4 5 5 2 5 8

Replace Winner And Replay 1 1 2 3 1 3 4 6 3 6 2 1 8 6 3 5 7 2 2 3 2 4 6 9 Replay matches on path to root. 2 4 5 5 2 5 8

Replace Winner And Replay 1 1 2 3 1 3 4 6 3 6 2 1 8 6 3 5 7 2 2 3 2 4 6 9 2 4 5 5 2 5 Opponent is player who lost last match played at this node. 8

Time To Sort • • Initialize winner tree: O(n) time Remove winner and replay: O(logn) time Remove winner and replay n times : O(nlogn) time Thus, the total sort time is O(nlogn)

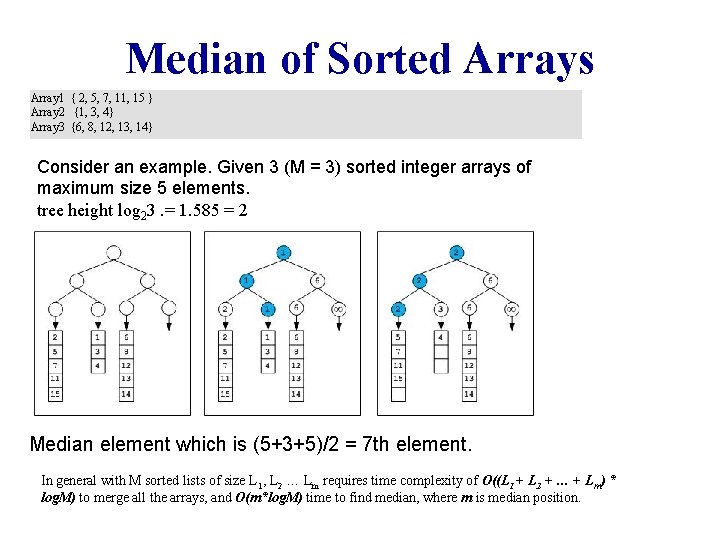
Median of Sorted Arrays • Tournament tree can effectively be used to find median of sorted arrays. Assume, given M sorted arrays of equal size L (for simplicity). We can attach all these sorted arrays to the tournament tree, one array per leaf. We need a tree of height CEIL (log 2 M) to have at least M external nodes.

Median of Sorted Arrays Array 1 { 2, 5, 7, 11, 15 } Array 2 {1, 3, 4} Array 3 {6, 8, 12, 13, 14} Consider an example. Given 3 (M = 3) sorted integer arrays of maximum size 5 elements. tree height log 23. = 1. 585 = 2 Median element which is (5+3+5)/2 = 7 th element. In general with M sorted lists of size L 1, L 2 … Lm requires time complexity of O((L 1 + L 2 + … + Lm) * log. M) to merge all the arrays, and O(m*log. M) time to find median, where m is median position.

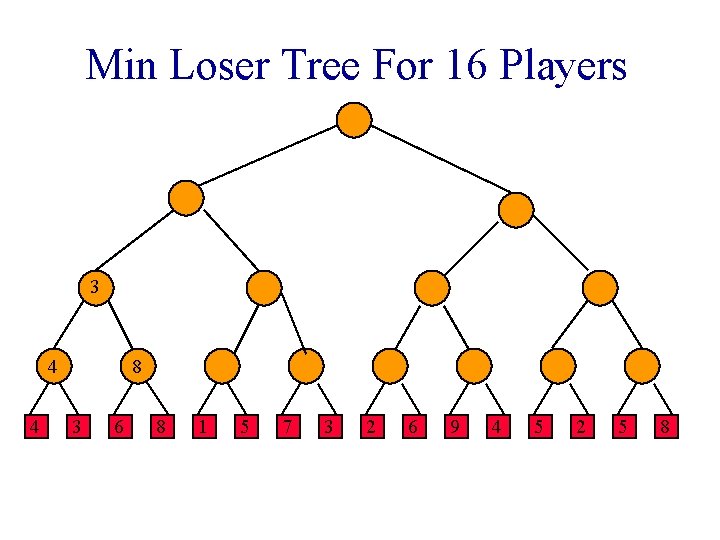
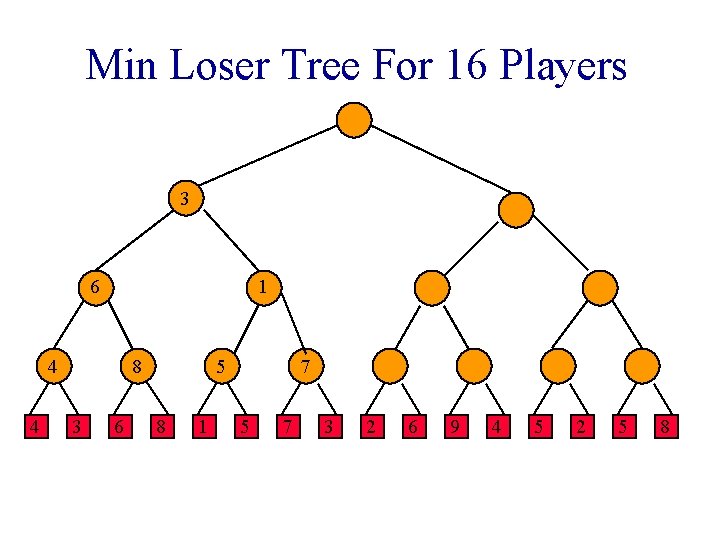
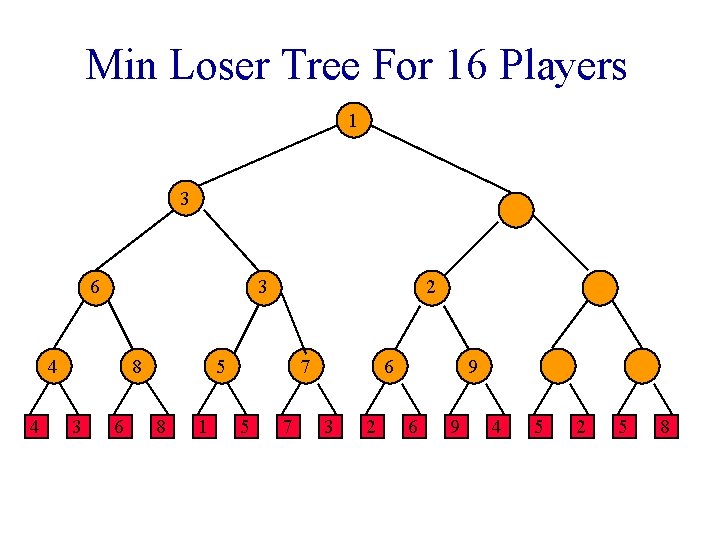
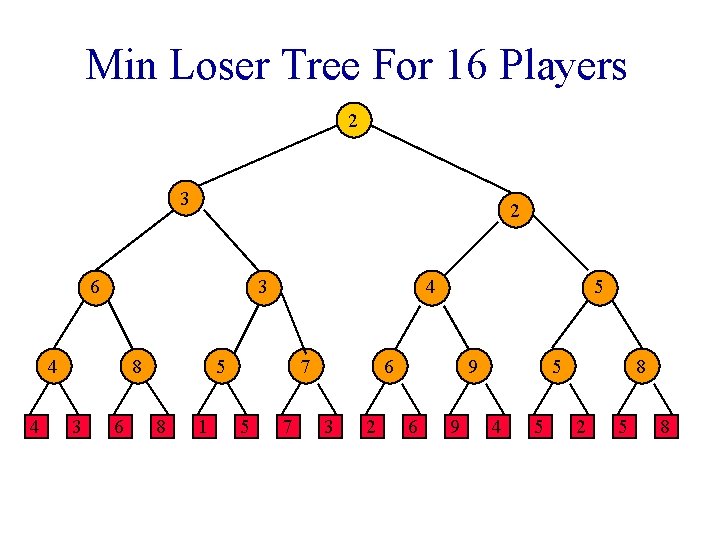
Loser Tree Each match node stores the match loser rather than the match winner.

Min Loser Tree For 16 Players 3 4 4 8 3 6 8 1 5 7 3 2 6 9 4 5 2 5 8

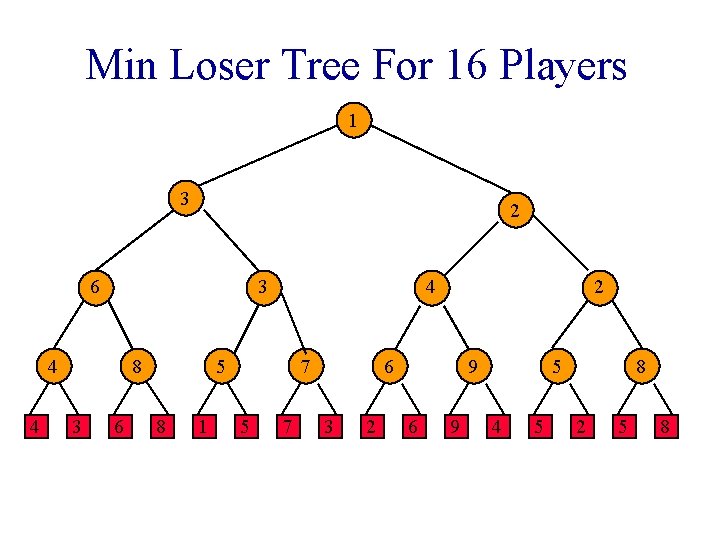
Min Loser Tree For 16 Players 3 6 1 4 4 8 3 6 5 8 1 7 5 7 3 2 6 9 4 5 2 5 8

Min Loser Tree For 16 Players 1 3 6 3 4 4 8 3 6 2 5 8 1 7 5 7 6 3 2 9 6 9 4 5 2 5 8

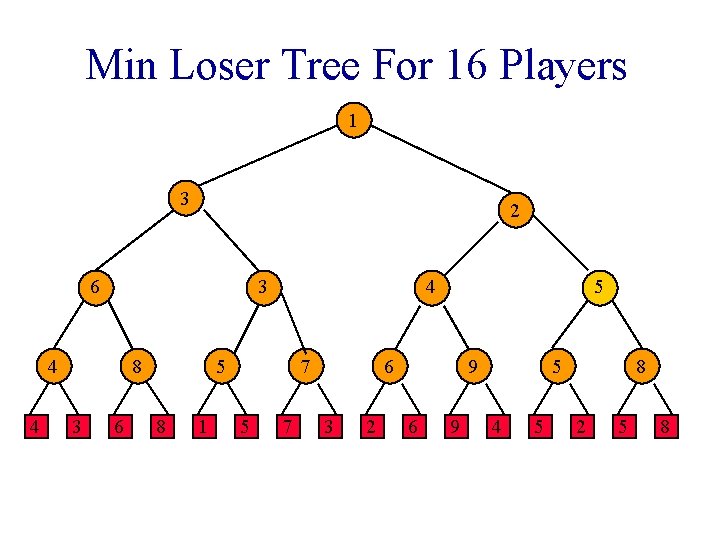
Min Loser Tree For 16 Players 1 3 2 6 3 4 4 8 3 6 4 5 8 1 7 5 7 2 6 3 2 9 6 9 5 4 5 8 2 5 8

Min Loser Tree For 16 Players 1 3 2 6 3 4 4 8 3 6 4 5 8 1 7 5 6 3 2 9 6 9 5 4 5 8 2 5 8

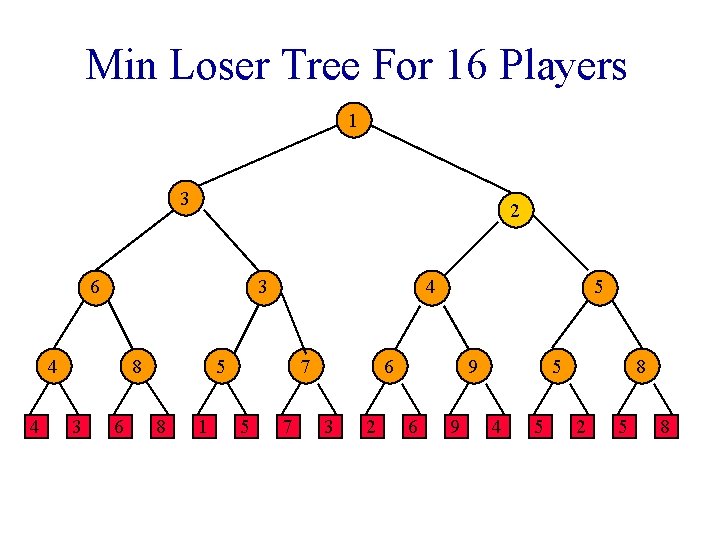
Min Loser Tree For 16 Players 1 3 2 6 3 4 4 8 3 6 4 5 8 1 7 5 6 3 2 9 6 9 5 4 5 8 2 5 8

Min Loser Tree For 16 Players 2 3 2 6 3 4 4 8 3 6 4 5 8 1 7 5 6 3 2 9 6 9 5 4 5 8 2 5 8

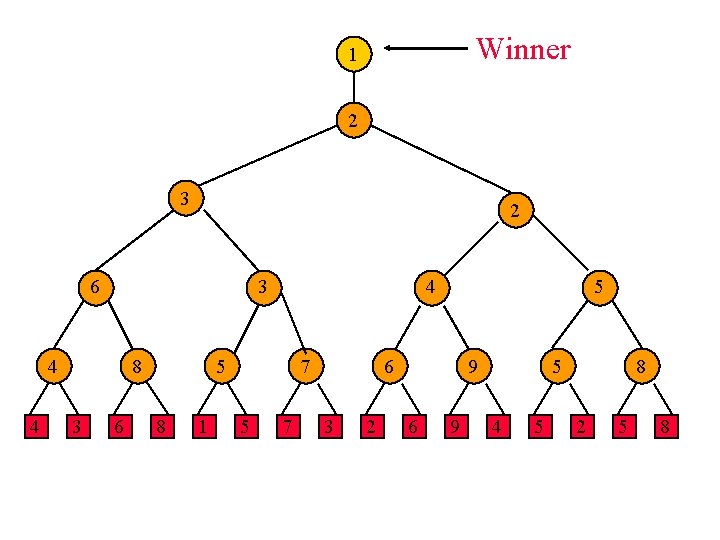
Winner 1 2 3 2 6 3 4 4 8 3 6 4 5 8 1 7 5 6 3 2 9 6 9 5 4 5 8 2 5 8

Complexity Of Loser Tree Initialize • • One match at each match node. One store of a left child winner. Total time is O(n). More precisely Theta(n).

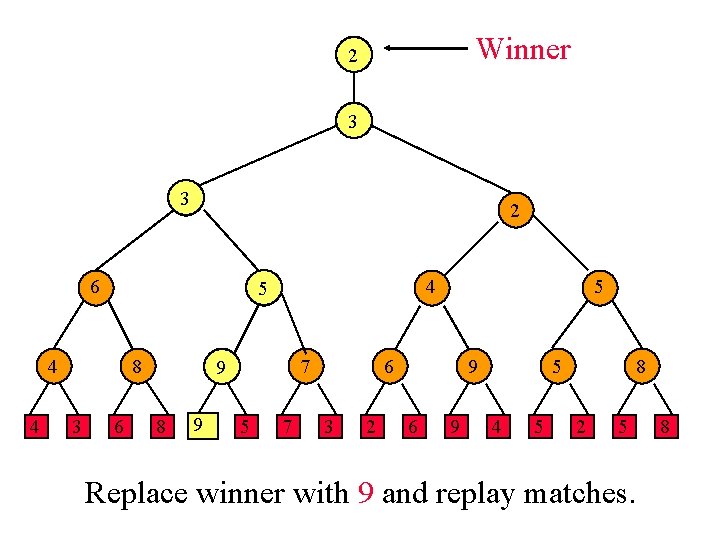
Winner 21 32 3 2 6 53 4 4 8 3 6 4 95 8 91 7 5 6 3 2 9 6 9 5 4 5 8 2 5 Replace winner with 9 and replay matches. 8

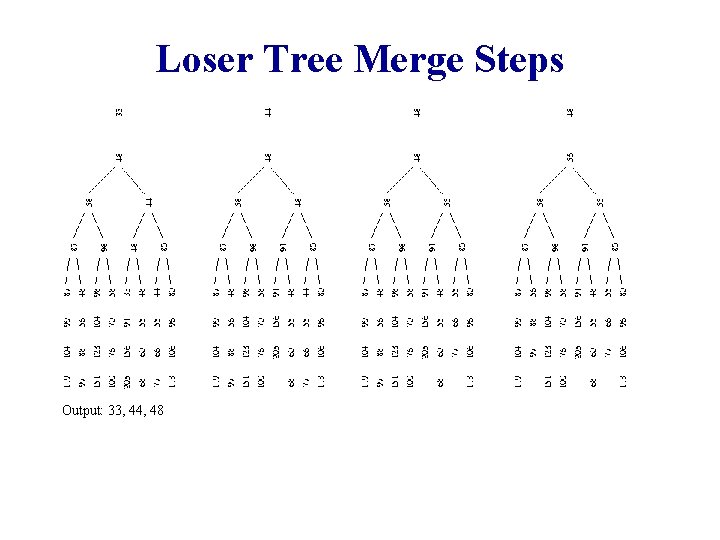
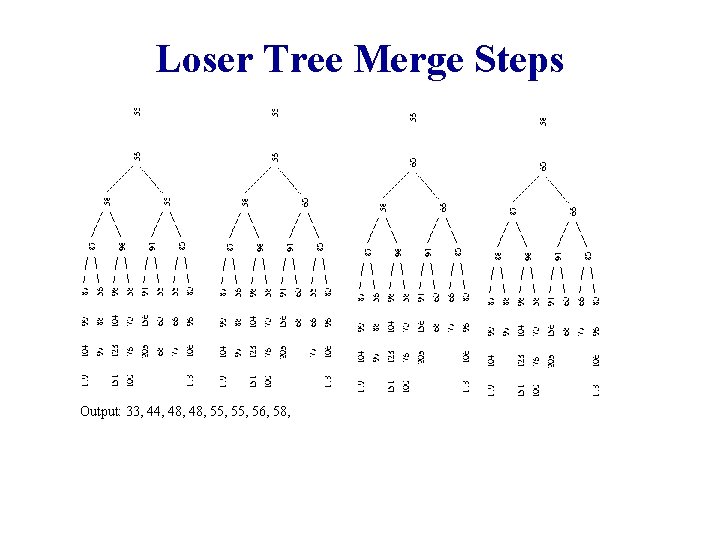
Loser Tree Merge Steps Output: 33, 44, 48

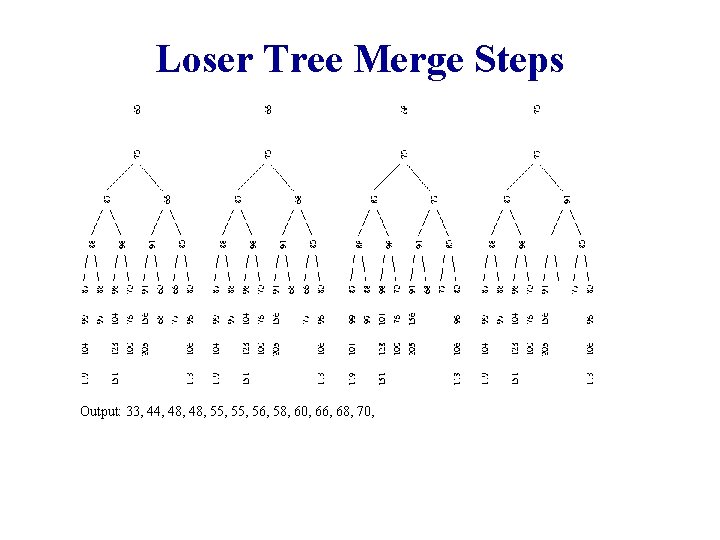
Loser Tree Merge Steps Output: 33, 44, 48, 55, 56, 58,

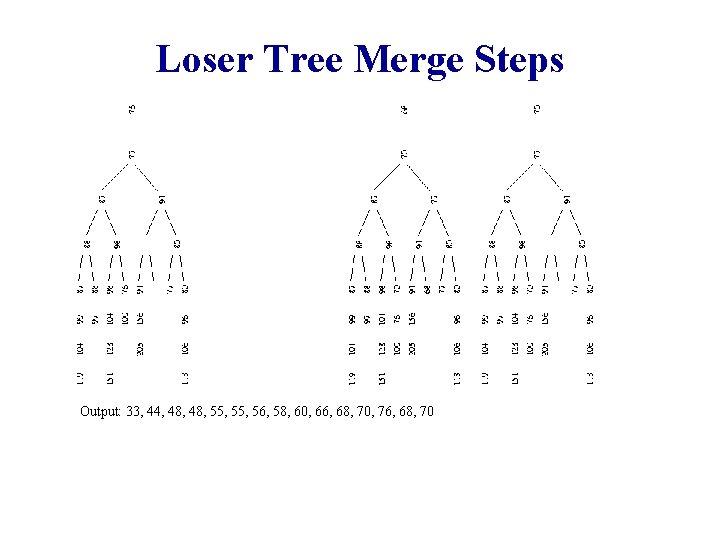
Loser Tree Merge Steps Output: 33, 44, 48, 55, 56, 58, 60, 66, 68, 70,

Loser Tree Merge Steps Output: 33, 44, 48, 55, 56, 58, 60, 66, 68, 70, 76, 68, 70

Complexity Of Replay • One match at each level that has a match node. • O(log n) • More precisely Theta(log n).

More Selection Tree Applications • k-way merging of runs during an external merge sort • Truck loading

Truck Loading § § n packages to be loaded into trucks each package has a weight each truck has a capacity of c tons minimize number of trucks

Truck Loading n = 5 packages weights [2, 5, 6, 3, 4] truck capacity c = 10 Load packages from left to right. If a package doesn’t fit into current truck, start loading a new truck.

Truck Loading n = 5 packages weights [2, 5, 6, 3, 4] truck capacity c = 10 truck 1 = [2, 5] truck 2 = [6, 3] truck 3 = [4] uses 3 trucks when 2 trucks suffice

Truck Loading n = 5 packages weights [2, 5, 6, 3, 4] truck capacity c = 10 truck 1 = [2, 5, 3] truck 2 = [6, 4]

Bin Packing • • n items to be packed into bins each item has a size each bin has a capacity of c minimize number of bins

Bin Packing Truck loading is same as bin packing. Truck is a bin that is to be packed (loaded). Package is an item/element. Bin packing to minimize number of bins is NP-hard. Several fast heuristics have been proposed.

Bin Packing Approximation Algorithms • • First Fit (FF) First Fit Decreasing (FFD) Best Fit (BF) Best Fit Decreasing (BFD) 60

Bin Packing Heuristics • First Fit. § Bins are arranged in left to right order. § Items are packed one at a time in given order. § Current item is packed into leftmost bin into which it fits. § If there is no bin into which current item fits, start a new bin.

First Fit n = 4 weights = [4, 7, 3, 6] capacity = 10 Pack red item into first bin.

First Fit n = 4 weights = [4, 7, 3, 6] capacity = 10 Pack blue item next. Doesn’t fit, so start a new bin.

First Fit n = 4 weights = [4, 7, 3, 6] capacity = 10

First Fit n = 4 weights = [4, 7, 3, 6] capacity = 10 Pack yellow item into first bin.

First Fit n = 4 weights = [4, 7, 3, 6] capacity = 10 Pack green item. Need a new bin.

First Fit n = 4 weights = [4, 7, 3, 6] capacity = 10 Not optimal. 2 bins suffice.

Bin Packing Heuristics • First Fit Decreasing. § Items are sorted into decreasing order. § Then first fit is applied.

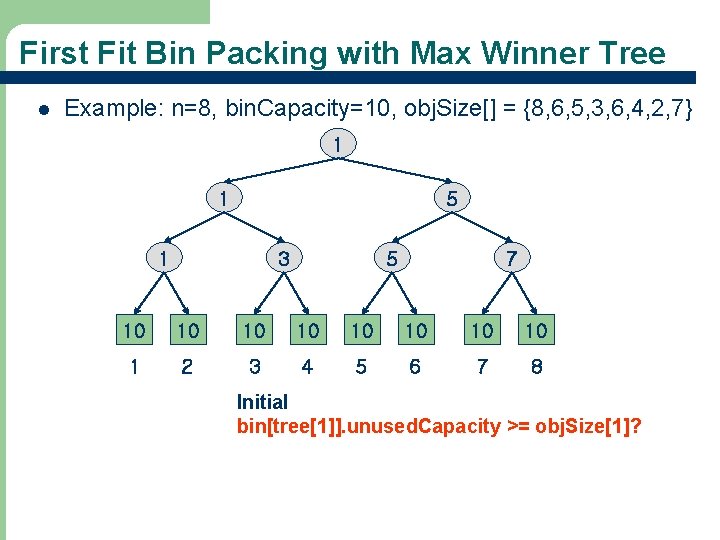
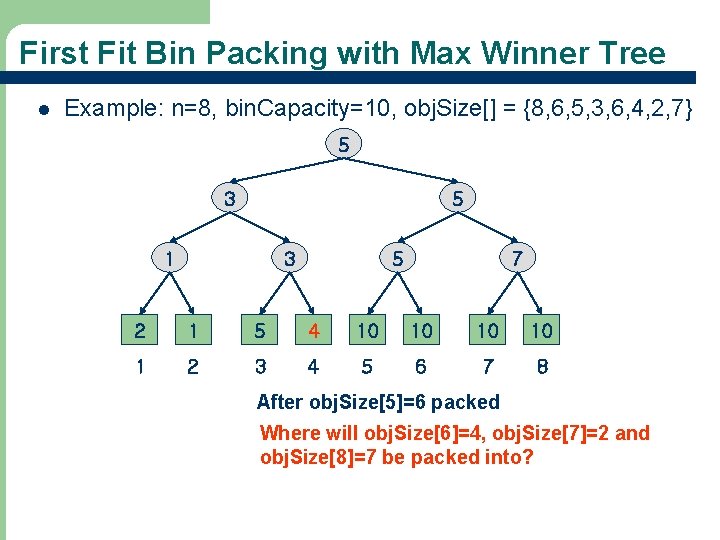
First Fit Bin Packing with Max Winner Tree l 69 Use a max winner tree in which the players are n bins and the value of a player is the available capacity bin. Capacity in the bin.

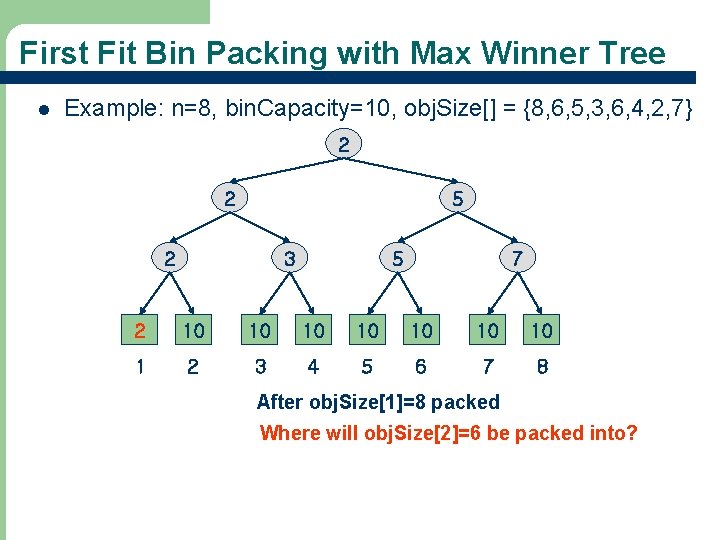
First Fit Bin Packing with Max Winner Tree l Example: n=8, bin. Capacity=10, obj. Size[] = {8, 6, 5, 3, 6, 4, 2, 7} 1 1 5 1 3 5 7 10 10 1 2 3 4 5 6 7 8 Initial bin[tree[1]]. unused. Capacity >= obj. Size[1]? 70

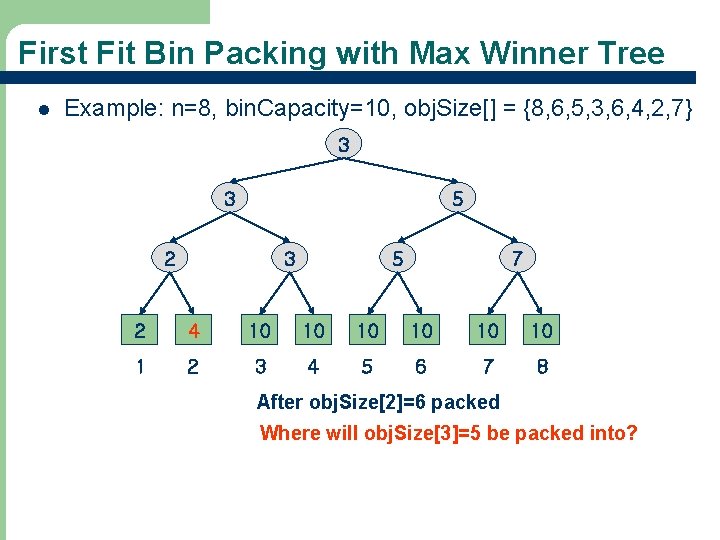
First Fit Bin Packing with Max Winner Tree l Example: n=8, bin. Capacity=10, obj. Size[] = {8, 6, 5, 3, 6, 4, 2, 7} 2 2 5 2 3 5 7 2 10 10 1 2 3 4 5 6 7 8 After obj. Size[1]=8 packed Where will obj. Size[2]=6 be packed into? 71

First Fit Bin Packing with Max Winner Tree l Example: n=8, bin. Capacity=10, obj. Size[] = {8, 6, 5, 3, 6, 4, 2, 7} 3 3 5 2 3 5 7 2 4 10 10 10 1 2 3 4 5 6 7 8 After obj. Size[2]=6 packed Where will obj. Size[3]=5 be packed into? 72

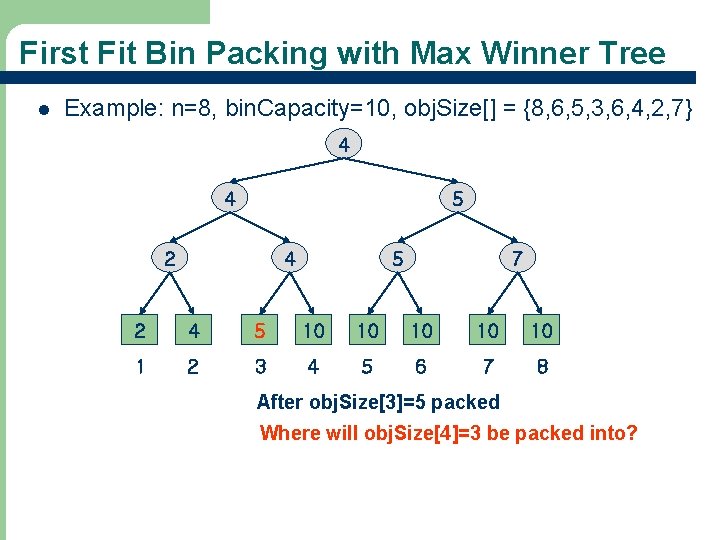
First Fit Bin Packing with Max Winner Tree l Example: n=8, bin. Capacity=10, obj. Size[] = {8, 6, 5, 3, 6, 4, 2, 7} 4 4 5 2 4 5 7 2 4 5 10 10 10 1 2 3 4 5 6 7 8 After obj. Size[3]=5 packed Where will obj. Size[4]=3 be packed into? 73

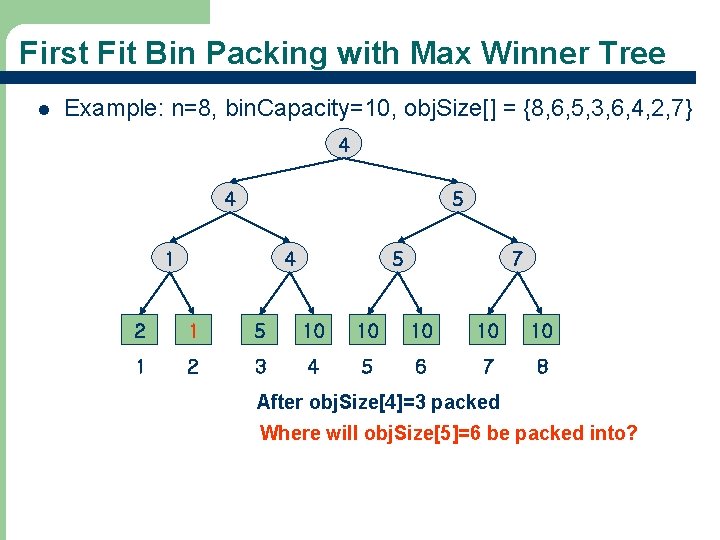
First Fit Bin Packing with Max Winner Tree l Example: n=8, bin. Capacity=10, obj. Size[] = {8, 6, 5, 3, 6, 4, 2, 7} 4 4 5 1 4 5 7 2 1 5 10 10 10 1 2 3 4 5 6 7 8 After obj. Size[4]=3 packed Where will obj. Size[5]=6 be packed into? 74

First Fit Bin Packing with Max Winner Tree l Example: n=8, bin. Capacity=10, obj. Size[] = {8, 6, 5, 3, 6, 4, 2, 7} 5 3 5 1 3 5 7 2 1 5 4 10 10 1 2 3 4 5 6 7 8 After obj. Size[5]=6 packed Where will obj. Size[6]=4, obj. Size[7]=2 and obj. Size[8]=7 be packed into? 75

Bin Packing Heuristics • Best Fit. § Items are packed one at a time in given order. § To determine the bin for an item, first determine set S of bins into which the item fits. § If S is empty, then start a new bin and put item into this new bin. § Otherwise, pack into bin of S that has least available capacity.

Bin Packing Heuristics • Best Fit Decreasing. § Items are sorted into decreasing order. § Then best fit is applied.

Performance • For first fit and best fit: Heuristic Bins <= (17/10)(Minimum Bins) + 2 • For first fit decreasing and best fit decreasing: Heuristic Bins <= (11/9)(Minimum Bins) + 4

Complexity Of First Fit Use a max tournament tree in which the players are n bins and the value of a player is the available capacity in the bin. O(n log n), where n is the number of items.

Select smallest one million elements from one billion unsorted elements: • As a simple solution, we can sort the billion numbers and select first one million. • On a limited memory system sorting billion elements and picking the first one million seems to be impractical. • We can use tournament tree approach. At any time only elements of tree to be in memory.

Select smallest one million elements from one billion unsorted elements: • Split the large array (perhaps stored on disk) into smaller size arrays of size one million each (or even smaller that can be sorted by the machine). • Sort these 1000 small size arrays and store them on disk as individual files. • Construct a tournament tree which can have atleast 1000 leaf nodes (tree to be of height 10 since 29 < 1000 < 210, if the individual file size is even smaller we will need more leaf nodes).

Select smallest one million elements from one billion unsorted elements: • Every leaf node will have an engine that picks next element from the sorted file stored on disk. We can play the tournament tree game to extract first one million elements. • Total cost = sorting 1000 lists of one million each + tree construction + tournaments • Implementation We need to build the tree in bottom-up manner. All the leaf nodes filled first. Start at the left extreme of tree and fill along the breadth (i. e. from 2 k-1 to 2 k – 1 where k is depth of tree) and play the game.