Chapter four Eulerian Hamiltonian Paths and Circuits in

Chapter four : Eulerian / Hamiltonian Paths and Circuits in a Graph § 4. 1. Euler Paths and Circuits § 4. 2. Hamiltonian Paths and Circuits 1 ENSA Agadir, 2014

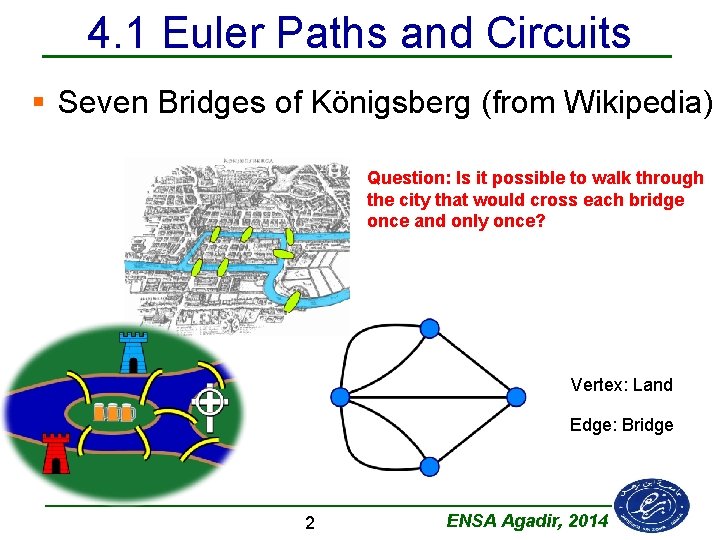
4. 1 Euler Paths and Circuits § Seven Bridges of Königsberg (from Wikipedia) Question: Is it possible to walk through the city that would cross each bridge once and only once? Vertex: Land Edge: Bridge 2 ENSA Agadir, 2014

4. 1 Euler Paths and Circuits § Euler path A path in a graph G is called an Euler path if it includes every edge exactly once. § Euler circuit An Euler circuit is an Euler path that is a circuit. About Leonhard Euler: http: //en. wikipedia. org/wiki/Leonhard_Euler 3 ENSA Agadir, 2014

4. 1 Euler Paths and Circuits § Example 1 4 ENSA Agadir, 2014

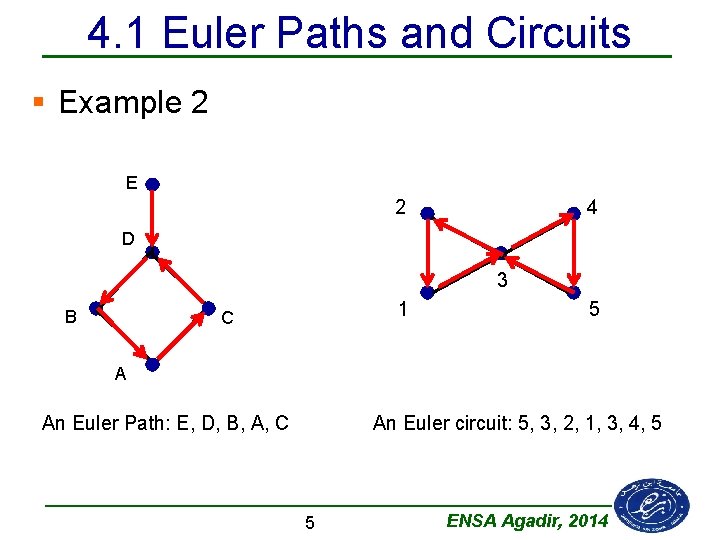
4. 1 Euler Paths and Circuits § Example 2 E 2 4 D 3 B 1 C 5 A An Euler Path: E, D, B, A, C An Euler circuit: 5, 3, 2, 1, 3, 4, 5 5 ENSA Agadir, 2014

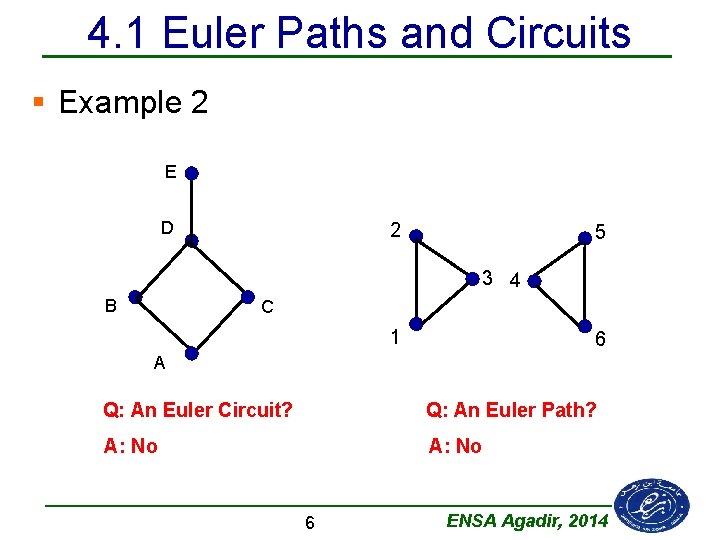
4. 1 Euler Paths and Circuits § Example 2 E D 2 5 3 4 B C 1 6 A Q: An Euler Circuit? Q: An Euler Path? A: No 6 ENSA Agadir, 2014

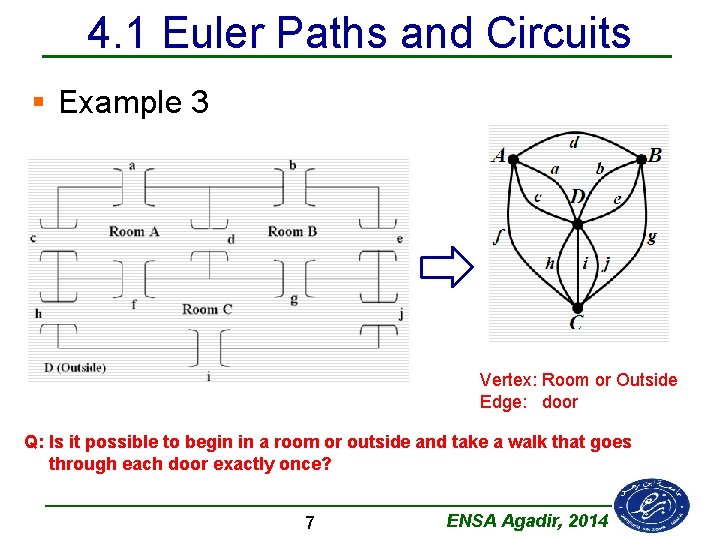
4. 1 Euler Paths and Circuits § Example 3 Vertex: Room or Outside Edge: door Q: Is it possible to begin in a room or outside and take a walk that goes through each door exactly once? 7 ENSA Agadir, 2014

4. 1 Euler Paths and Circuits § Two Questions 1. Is it possible to determine whether an Euler path or Euler circuit exists without actually finding it? Theorem 1 (Euler circuit) & Theorem 2 (Euler path) 2. If an Euler circuit exists, how to find it effectively? Fleury’s algorithm 8 ENSA Agadir, 2014

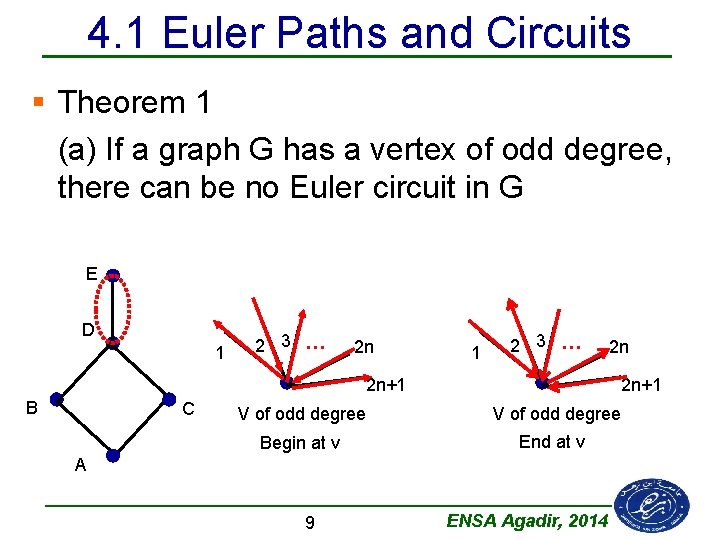
4. 1 Euler Paths and Circuits § Theorem 1 (a) If a graph G has a vertex of odd degree, there can be no Euler circuit in G E D 1 2 3 … 2 n 2 n+1 B C 2 n+1 V of odd degree Begin at v End at v A 9 ENSA Agadir, 2014

4. 1 Euler Paths and Circuits § Theorem 1 (b) If G is a connected graph and every vertex has even degree, then there is an Euler circuit in G. The Strategy of this proof (b) : Support there is a largest (smallest) object and construct a larger (smaller) object of the same type thereby creating a contradiction. 10 ENSA Agadir, 2014

4. 1 Euler Paths and Circuits § Proof (b). Basic Step: |V|=1, 2 is true (why? ) Induction Step : |V|=1, 2…k is true |V|=k+1 is true 1. Assume G is connected and has more than one vertex, then there exists a simple path having the longest possible length (why? ). Let its vertex sequence п 0: v 1 v 2, …, vs. Since vs has even degree and п 0 uses only one edge that has vs as a vertex, there must be an edge e not in п 0 that also has vs as a vertex. If the other vertex of e is not in п 0, then we can construct a simple path longer than п 0 (why? ), which is a contradiction. Thus e has some vi as its other vertex, and therefore we have a simple circuit vi vi+1, … vs, vi in G. 11 ENSA Agadir, 2014

4. 1 Euler Paths and Circuits 2. Choose the longest circuit п in G, and delete all edges in п (but no vertices). Assuming there is no Euler circuit in G, then п cannot contain all edges of G (why? ). Let G 1 be the graph formed from G by deleting all edges in п (but no vertices). Since п is a circuit, deleting its edges will reduce the degree of every vertex by 0 or 2, so G 1 is also a graph with all vertices of even degree. Choose any connected component in G 1 and call this graph G 2 (G 2 may be G 1). Then G 2 has also a circuit п’ (why? ). 12 ENSA Agadir, 2014

4. 1 Euler Paths and Circuits 3. Consider п and п’ in G case #1: if п and п’ have vertices in common, e. g. v’, then we can construct a circuit in G that is longer than п by combing п and п’ at v’ (contradiction!) case #1 v’ п П’ Case #2: If there is no common vertex in п and п’. Then |VG 2| < |VG|, then G 2 has a Euler Circuit (why? ) , then G becomes not connected (why? ) , which is a contradiction. Therefore, the assumption is wrong, namely, G has an Euler circuit. 13 ENSA Agadir, 2014

4. 1 Euler Paths and Circuits § Theorem 2 (a) If a graph G has more than two vertices of odd degree, then there is no Euler path in G. Proof: Let v 1, v 2, v 3 be vertices of odd degree. Any possible Euler path must leave (or arrive at) each of v 1, v 2, v 3 with no way to return (or leave) since each of these vertices has odd degree. One vertex of these three vertices may be the beginning of the Euler path and another the end, but this leaves the third vertex at one end of an untraveled edge. Thus there is no Euler path. 14 ENSA Agadir, 2014

4. 1 Euler Paths and Circuits § Theorem 2 (b) If G is connected and has exactly two vertices of odd degree, there is an Euler path in G. Any Euler path in G must begin at one vertex of odd degree and end at the other. Proof: Let u and v be the two vertices of odd degree. Adding the edge {u, v} to G produces a connected graph G’ all of whose vertices have even degree. By Theorem 1(b), there is an Euler circuit п’ in G’. Omitting {u, v} from п’ produces an Euler path that begins at u (or v) and ends at v (or u). 15 ENSA Agadir, 2014

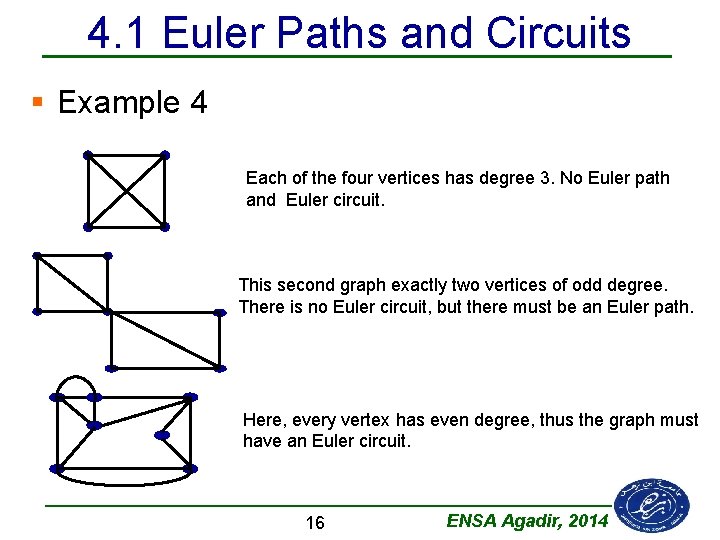
4. 1 Euler Paths and Circuits § Example 4 Each of the four vertices has degree 3. No Euler path and Euler circuit. This second graph exactly two vertices of odd degree. There is no Euler circuit, but there must be an Euler path. Here, every vertex has even degree, thus the graph must have an Euler circuit. 16 ENSA Agadir, 2014

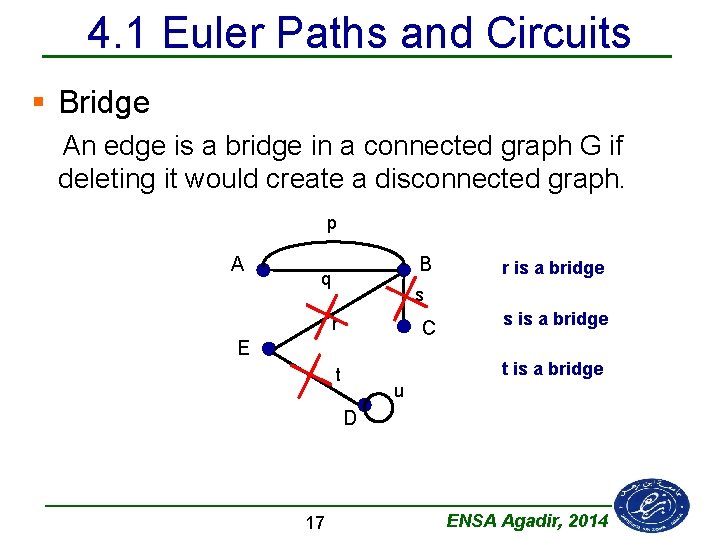
4. 1 Euler Paths and Circuits § Bridge An edge is a bridge in a connected graph G if deleting it would create a disconnected graph. p A B q r is a bridge s r C E s is a bridge t u D 17 ENSA Agadir, 2014

4. 1 Euler Paths and Circuits § FLEURY’S ALGORITHM Let G={V, E, γ} be a connected graph with each vertex of even degree. Step 1 Select an edge e 1 that is not a bridge in G. Let its vertices be v 1, v 2. Let п be specified by Vп: v 1, v 2 and Eп: e 1. Remove e 1 from E and let G 1 be the resulting subgraph of G. Step 2 Suppose that Vп: v 1, v 2 … vk and Eп: e 1 e 2 … ek-1 have been constructed so far, and that all of these edges and any resulting isolated vertices have been removed from V and E to form Gk-1. Since vk has even degree, and ek-1 ends there, there must be an edge ek in Gk-1 that also has vk as a vertex. If there is more than one such edge, select one that is not a bridge for Gk-1. Denote the vertex of ek other than vk by vk+1, Extend Vп: v 1, v 2 … vk vk+1 and Eп: e 1 e 2 … ek-1 ek. Step 3 repeat Step 2 until no edges remain in E 18 ENSA Agadir, 2014

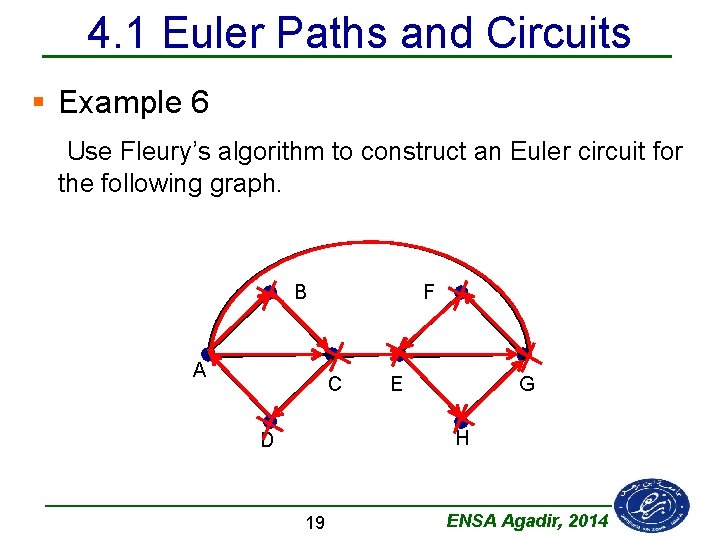
4. 1 Euler Paths and Circuits § Example 6 Use Fleury’s algorithm to construct an Euler circuit for the following graph. B A F C E G H D 19 ENSA Agadir, 2014

4. 1 Euler Paths and Circuits § Homework Ex. 6, Ex. 12, Ex. 14, Ex. 15, Ex. 21, Ex. 25 20 ENSA Agadir, 2014

4. 2 Hamiltonian Paths & Circuits § Hamiltonian path A Hamiltonian path is a path that contains each vertex exactly once. § Hamiltonian circuit A Hamiltonian circuit is a circuit that contains each vertex exactly once except for the first vertex. 21 ENSA Agadir, 2014

4. 2 Hamiltonian Paths & Circuits § Loop and Multiple edges Loops and multiple edges are of no use in finding Hamiltonian circuits, since loops Could not be used, and only one edge can be used between any two vertices. Thus we suppose that any graph in this section has no loops or multiple edges. 22 ENSA Agadir, 2014

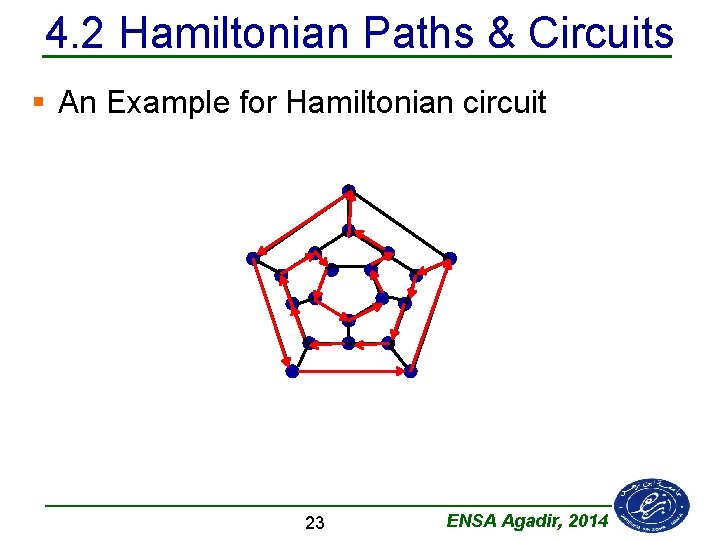
4. 2 Hamiltonian Paths & Circuits § An Example for Hamiltonian circuit 23 ENSA Agadir, 2014

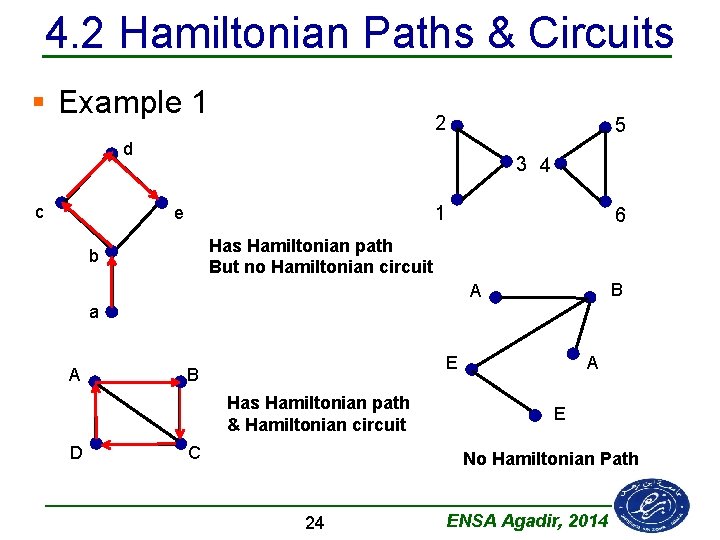
4. 2 Hamiltonian Paths & Circuits § Example 1 2 5 d c 3 4 1 e 6 Has Hamiltonian path But no Hamiltonian circuit b B A a A E B Has Hamiltonian path & Hamiltonian circuit D C A E No Hamiltonian Path 24 ENSA Agadir, 2014

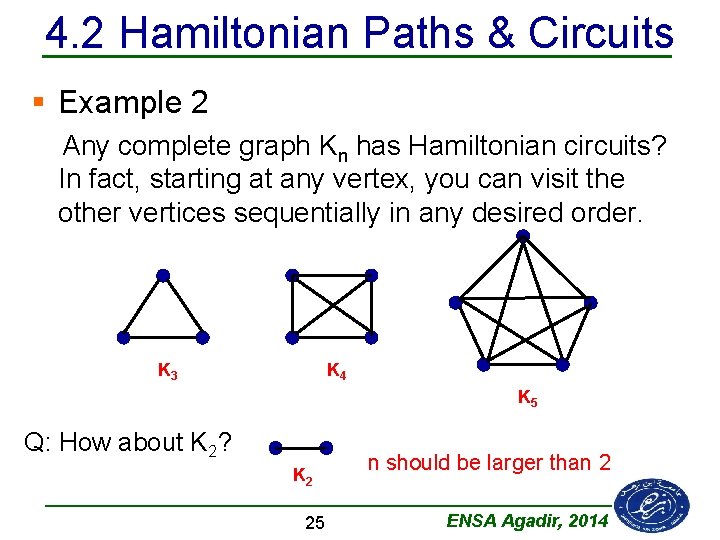
4. 2 Hamiltonian Paths & Circuits § Example 2 Any complete graph Kn has Hamiltonian circuits? In fact, starting at any vertex, you can visit the other vertices sequentially in any desired order. K 3 K 4 K 5 Q: How about K 2? K 2 25 n should be larger than 2 ENSA Agadir, 2014

4. 2 Hamiltonian Paths & Circuits § Two Questions 1. Is it possible to determine whether a Hamiltonian path or circuit exists? has not been completely answered 2. If there must be a Hamiltonian path or circuit, is there an efficient way to find it? is still unanswered. 26 ENSA Agadir, 2014

4. 2 Hamiltonian Paths & Circuits § Theorem 1 Let G be a connected graph with n vertices, n>2, and no loops or multiple edges. G has a Hamiltonian circuit if for any two vertices u and v of G that are not adjacent, the degree of u plus the degree of v is greater than or equal to n. Corollary 1 G has a Hamiltonian circuit if each vertex has degree greater than or equal to n/2. 27 ENSA Agadir, 2014

4. 2 Hamiltonian Paths & Circuits § Theorem 2 Let the number of edges of G be m. Then G has a Hamiltonian circuit if m ≥ (n 2 -3 n+6)/2, where n is the number of vertices Proof: Support u & v are non-adjacent vertices in G. Let deg(x) for the degree of x. Let H be the graph produced by eliminating u and v from G along with any edges that have u or v as end points. Then H has n-2 vertices and mdeg(u) –deg(v) edges. The maximum number of edges that H could possibly have is 2 -5 n+6 ) And then we have m – deg(u)-deg(v) <= ½(n ENSA Agadir, 2014 28

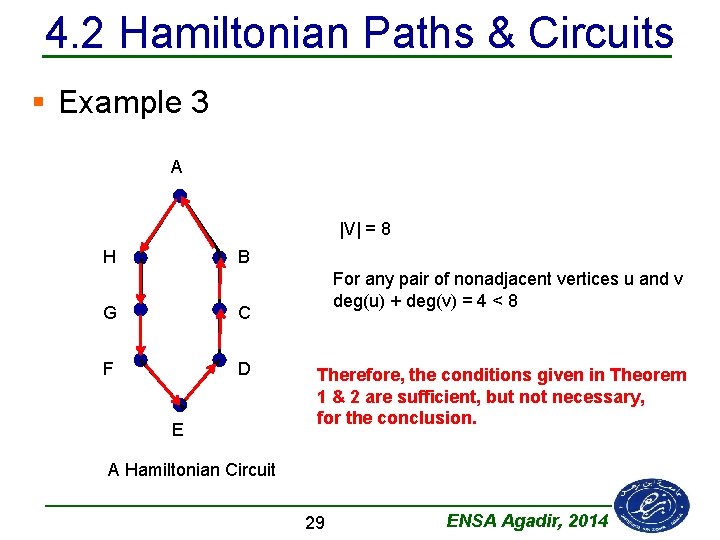
4. 2 Hamiltonian Paths & Circuits § Example 3 A |V| = 8 H B G C F D E For any pair of nonadjacent vertices u and v deg(u) + deg(v) = 4 < 8 Therefore, the conditions given in Theorem 1 & 2 are sufficient, but not necessary, for the conclusion. A Hamiltonian Circuit 29 ENSA Agadir, 2014

4. 2 Hamiltonian Paths & Circuits § Traveling salesperson problem Find a Hamiltonian circuit (or path) for which the total sum of weights in the path is a minimum. For example, the vertices might represent cities, the edges, lines of transportation, and the weight of an edge, the cost of traveling along the edge. B D 2 6 3 2 A 2 5 E C 5 4 F 30 6 3 4 H G ENSA Agadir, 2014

4. 2 Hamiltonian Paths and Circuits § Homework Ex. 8, Ex. 13, Ex. 18, Ex. 20, Ex. 21 31 ENSA Agadir, 2014