Discrete Maths Chapter 4 Finding the Shortest Path

Discrete Maths Chapter 4: Finding the Shortest Path Lesson 1: Dijkstra’s Algorithm

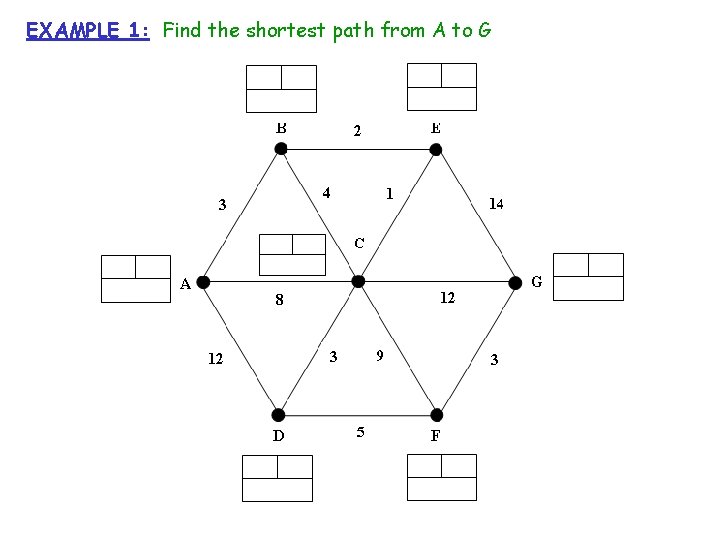
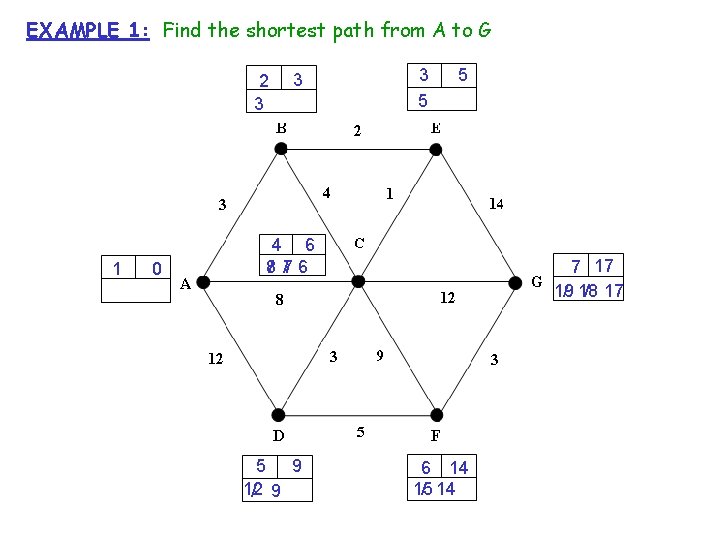
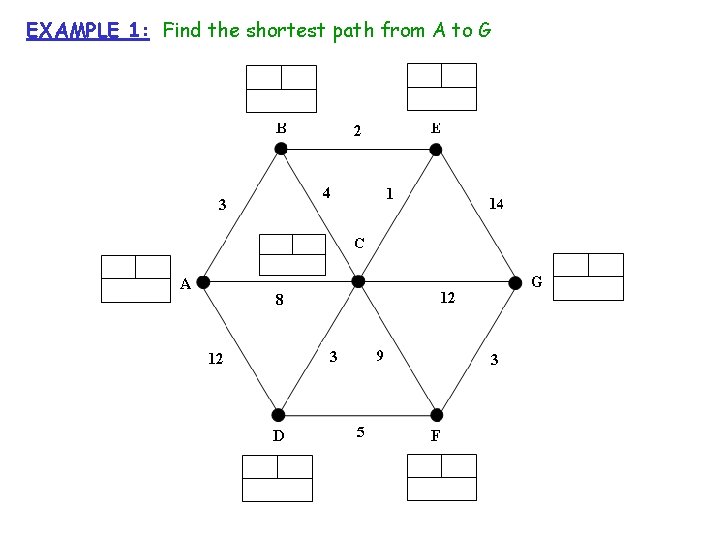
EXAMPLE 1: Find the shortest path from A to G

Dijkstra’s Algorithm • Dijkstra’s algorithm is used in problems relating to finding the shortest path. • Each node is given a temporary label denoting the length of the shortest path from the start node so far. • This label is replaced if another shorter route is found. • Once it is certain that no other shorter paths can be found, the temporary label becomes a permanent label. • Eventually all the nodes have permanent labels. • At this point the shortest path is found by retracing the path backwards.

Dijkstra’s Algorithm Aim: To find the shortest path connecting two nodes • Step 1: Label the start node with zero and box this label. • Step 2: Consider the node with the most recently boxed label. Suppose this node to be X and let D be its permanent label. Then, in turn, consider each node directly joined to X but not yet permanently boxed. For each such node, Y say, temporarily label it with the lesser of D + (the weight of arc XY) and its existing label (if any). • Step 3: Choose the least of all temporary labels on the network. Make this label permanent by boxing it. • Step 4: Repeat Steps 2 and 3 until the destination node has a permanent label. • Step 5: Go backwards through the network, retracing the path of shortest length from the destination node to the start node.

EXAMPLE 1: Find the shortest path from A to G 2 3 1 0 3 3 5 5 4 6 8/ 7 / 6 5 9 12 / 9 7 17 / 17 19 / 18 6 14 15 / 14

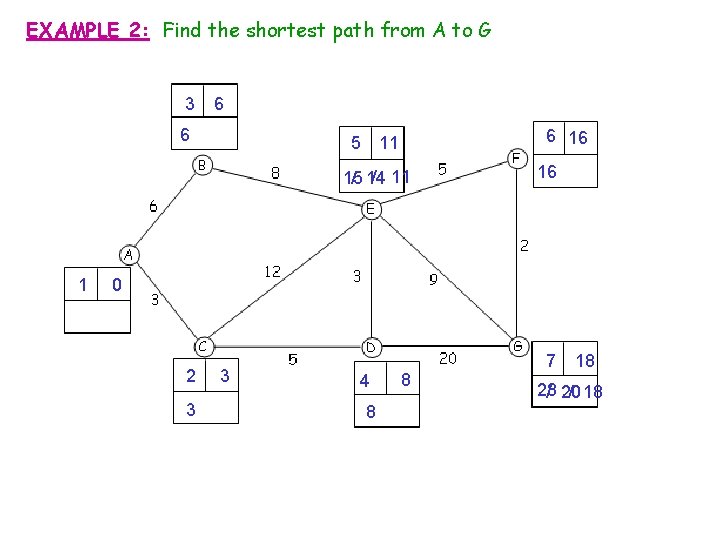
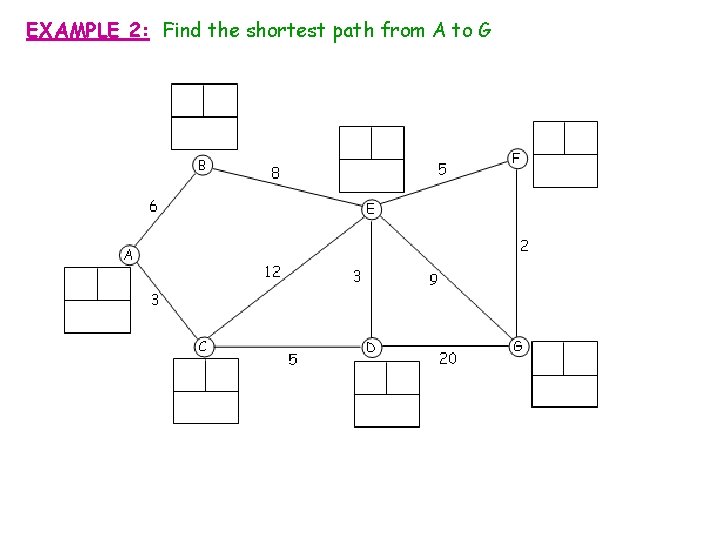
EXAMPLE 2: Find the shortest path from A to G 3 6 6 6 16 5 11 / 11 15 / 14 1 16 0 2 3 3 4 8 8 7 18 28 / 20 / 18

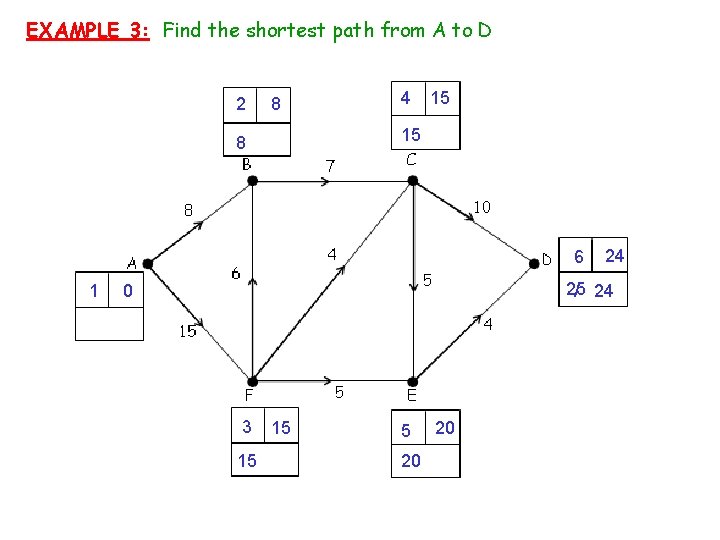
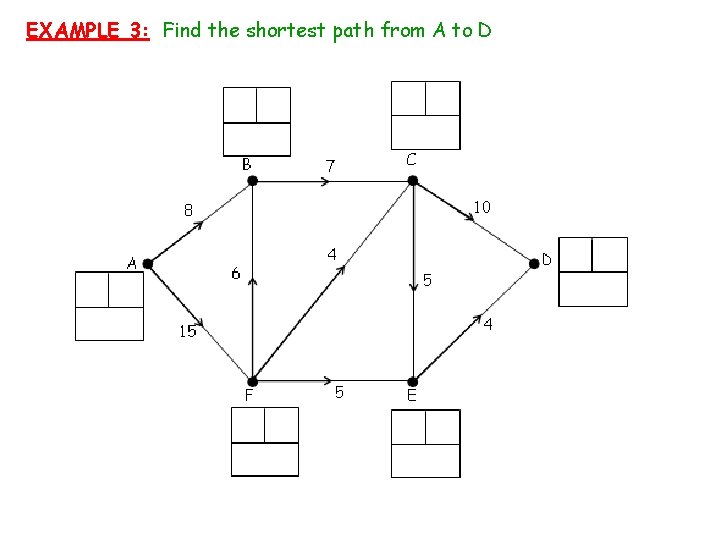
EXAMPLE 3: Find the shortest path from A to D 2 8 4 15 15 8 6 1 24 25 / 24 0 3 15 15 5 20 20

EXAMPLE 1: Find the shortest path from A to G

EXAMPLE 2: Find the shortest path from A to G

EXAMPLE 3: Find the shortest path from A to D