Path Analysis Why path analysis for test case

Path Analysis • Why path analysis for test case design? – Provides a systematic methodology. • Reproducible • Traceable • Countable • What is path analysis? – Analyzes the number of paths that exist in the system – Facilitates the decision process of how many paths to include in the test

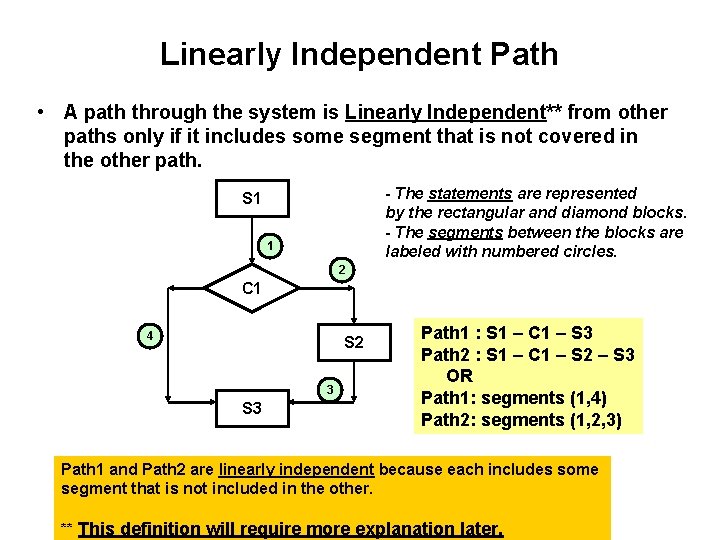
Linearly Independent Path • A path through the system is Linearly Independent** from other paths only if it includes some segment that is not covered in the other path. - The statements are represented by the rectangular and diamond blocks. - The segments between the blocks are labeled with numbered circles. S 1 1 2 C 1 4 S 2 3 S 3 Path 1 : S 1 – C 1 – S 3 Path 2 : S 1 – C 1 – S 2 – S 3 OR Path 1: segments (1, 4) Path 2: segments (1, 2, 3) Path 1 and Path 2 are linearly independent because each includes some segment that is not included in the other. ** This definition will require more explanation later.

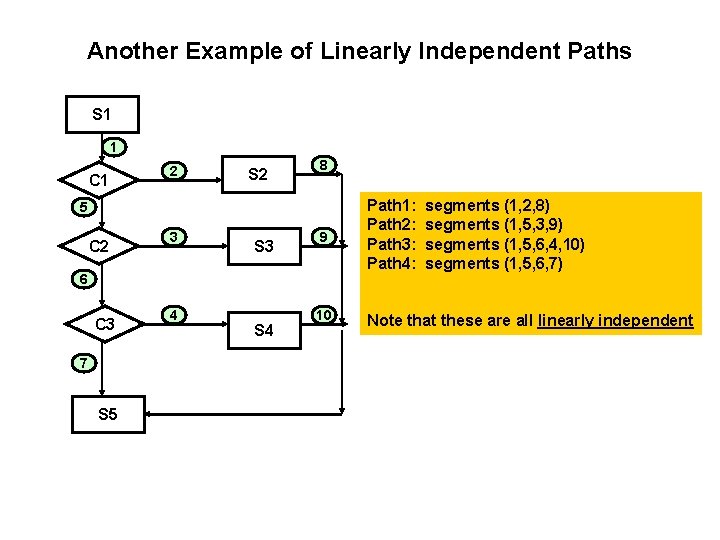
Another Example of Linearly Independent Paths S 1 1 C 1 2 S 2 8 9 Path 1: Path 2: Path 3: Path 4: 10 Note that these are all linearly independent 5 C 2 3 S 3 6 C 3 7 S 5 4 S 4 segments (1, 2, 8) segments (1, 5, 3, 9) segments (1, 5, 6, 4, 10) segments (1, 5, 6, 7)

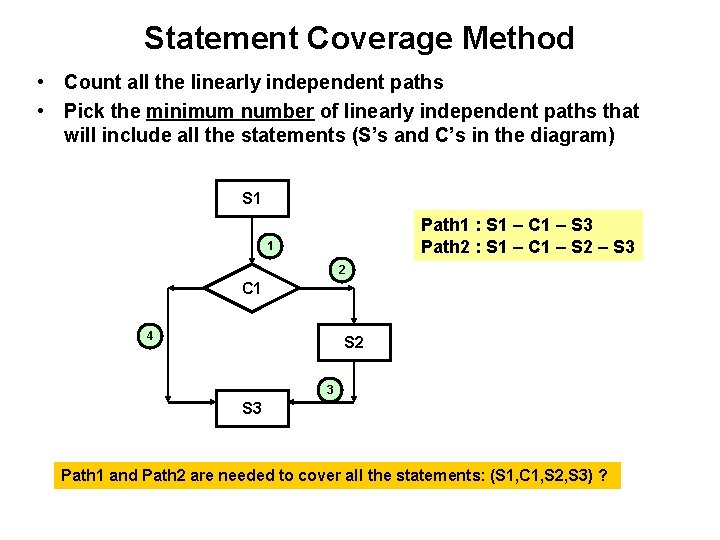
Statement Coverage Method • Count all the linearly independent paths • Pick the minimum number of linearly independent paths that will include all the statements (S’s and C’s in the diagram) S 1 Path 1 : S 1 – C 1 – S 3 Path 2 : S 1 – C 1 – S 2 – S 3 1 2 C 1 4 S 2 3 S 3 Path 1 and Path 2 are needed to cover all the statements: (S 1, C 1, S 2, S 3) ?

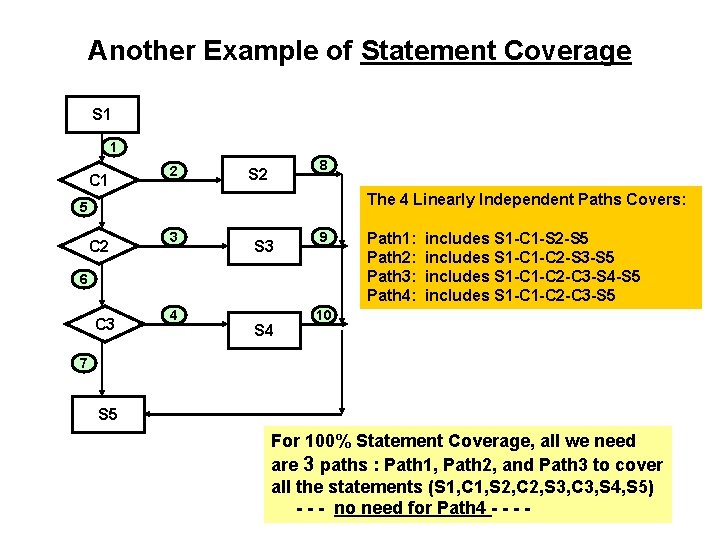
Another Example of Statement Coverage S 1 1 C 1 2 8 S 2 The 4 Linearly Independent Paths Covers: 5 C 2 3 S 3 9 6 C 3 4 S 4 Path 1: Path 2: Path 3: Path 4: includes S 1 -C 1 -S 2 -S 5 includes S 1 -C 2 -S 3 -S 5 includes S 1 -C 2 -C 3 -S 4 -S 5 includes S 1 -C 2 -C 3 -S 5 10 7 S 5 For 100% Statement Coverage, all we need are 3 paths : Path 1, Path 2, and Path 3 to cover all the statements (S 1, C 1, S 2, C 2, S 3, C 3, S 4, S 5) - - - no need for Path 4 - -

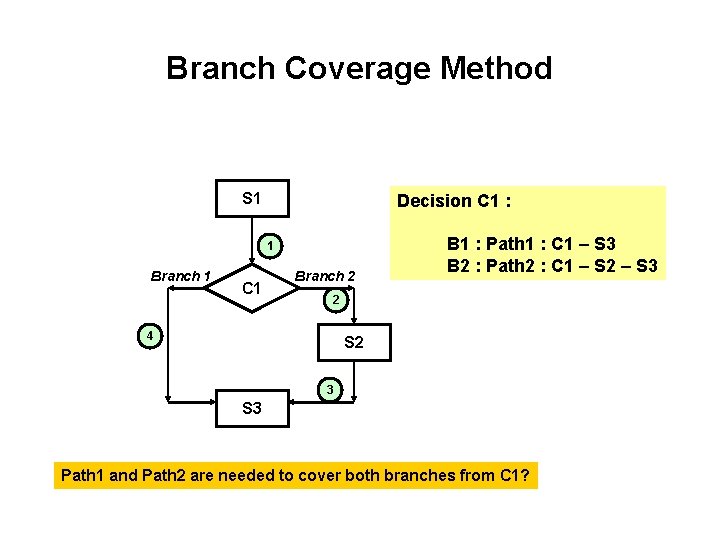
Branch Coverage Method • Identify all the decisions • Count all the branches from the each of the decisions • Pick the minimum number of paths that will cover all the branches from the decisions.

Branch Coverage Method S 1 Decision C 1 : 1 Branch 1 C 1 Branch 2 B 1 : Path 1 : C 1 – S 3 B 2 : Path 2 : C 1 – S 2 – S 3 2 4 S 2 3 S 3 Path 1 and Path 2 are needed to cover both branches from C 1?

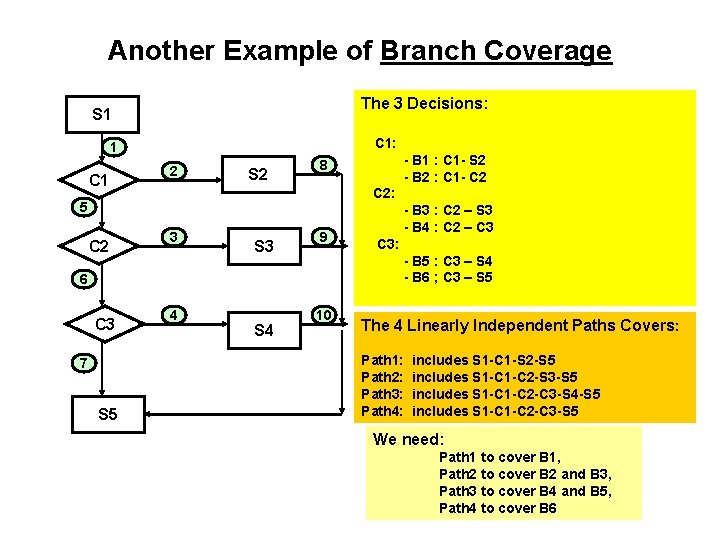
Another Example of Branch Coverage The 3 Decisions: S 1 C 1: 1 C 1 2 S 2 C 2: 5 C 2 3 S 3 9 7 S 5 4 S 4 - B 3 : C 2 – S 3 - B 4 : C 2 – C 3: - B 5 : C 3 – S 4 - B 6 ; C 3 – S 5 6 C 3 - B 1 : C 1 - S 2 - B 2 : C 1 - C 2 8 10 The 4 Linearly Independent Paths Covers: Path 1: Path 2: Path 3: Path 4: includes S 1 -C 1 -S 2 -S 5 includes S 1 -C 2 -S 3 -S 5 includes S 1 -C 2 -C 3 -S 4 -S 5 includes S 1 -C 2 -C 3 -S 5 We need: Path 1 to cover B 1, Path 2 to cover B 2 and B 3, Path 3 to cover B 4 and B 5, Path 4 to cover B 6

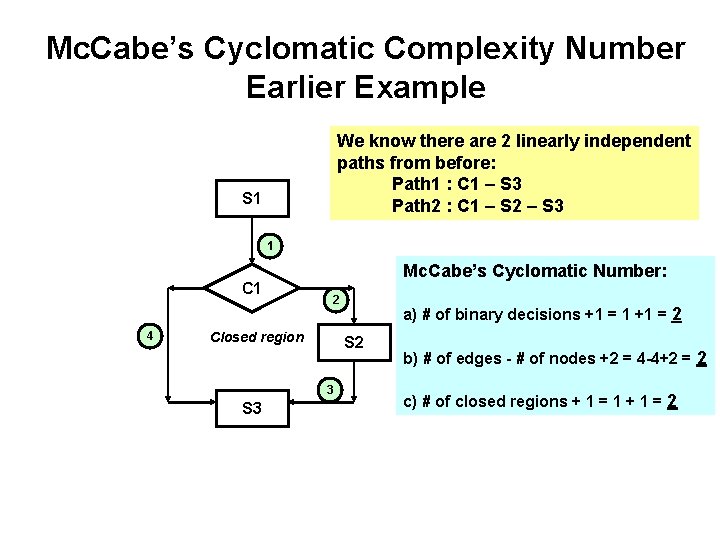
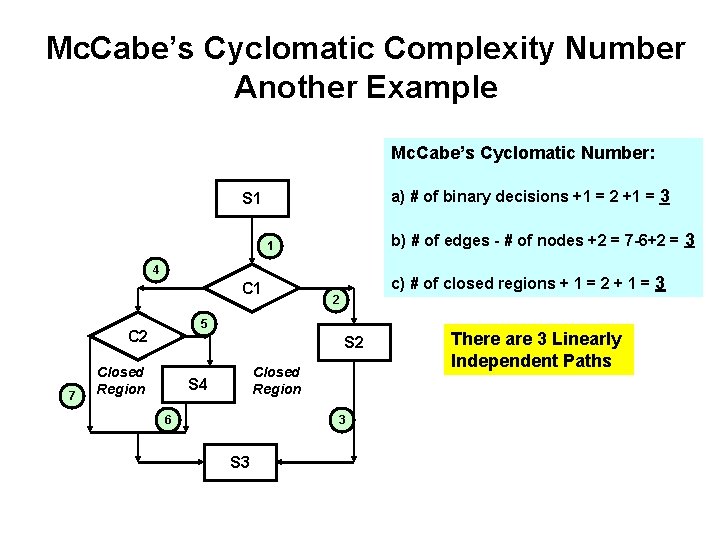
Mc. Cabe’s Cyclomatic Number • Is there a way to know how many linearly independent paths exist? – Mc. Cabe’s Cyclomatic number used to study program complexity may be applied. There are 3 ways to get the Cyclomatic Complexity number from a flow diagram. • # of binary decisions + 1 • # of edges - # of nodes + 2 • # of closed regions + 1 - Reference: T. J. Mc. Cabe, “A complexity Measure, ” IEEE Transactions on Software Engineering, Dec. 1976

Mc. Cabe’s Cyclomatic Complexity Number Earlier Example We know there are 2 linearly independent paths from before: Path 1 : C 1 – S 3 Path 2 : C 1 – S 2 – S 3 S 1 1 C 1 4 Mc. Cabe’s Cyclomatic Number: 2 Closed region S 2 3 S 3 a) # of binary decisions +1 = 1 +1 = 2 b) # of edges - # of nodes +2 = 4 -4+2 = 2 c) # of closed regions + 1 = 1 + 1 = 2

Mc. Cabe’s Cyclomatic Complexity Number Another Example Mc. Cabe’s Cyclomatic Number: a) # of binary decisions +1 = 2 +1 = 3 S 1 b) # of edges - # of nodes +2 = 7 -6+2 = 3 1 4 C 1 2 5 C 2 7 c) # of closed regions + 1 = 2 + 1 = 3 S 2 Closed Region S 4 6 3 S 3 There are 3 Linearly Independent Paths

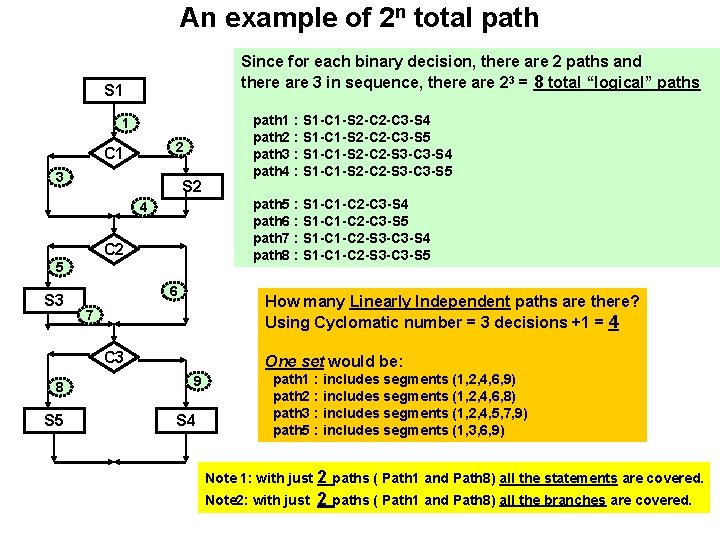
An example of 2 n total path Since for each binary decision, there are 2 paths and there are 3 in sequence, there are 23 = 8 total “logical” paths S 1 1 2 C 1 3 S 2 path 5 : S 1 -C 2 -C 3 -S 4 path 6 : S 1 -C 2 -C 3 -S 5 path 7 : S 1 -C 2 -S 3 -C 3 -S 4 path 8 : S 1 -C 2 -S 3 -C 3 -S 5 4 C 2 5 S 3 6 How many Linearly Independent paths are there? Using Cyclomatic number = 3 decisions +1 = 4 7 C 3 8 S 5 path 1 : S 1 -C 1 -S 2 -C 3 -S 4 path 2 : S 1 -C 1 -S 2 -C 3 -S 5 path 3 : S 1 -C 1 -S 2 -C 2 -S 3 -C 3 -S 4 path 4 : S 1 -C 1 -S 2 -C 2 -S 3 -C 3 -S 5 One set would be: 9 S 4 path 1 : includes segments (1, 2, 4, 6, 9) path 2 : includes segments (1, 2, 4, 6, 8) path 3 : includes segments (1, 2, 4, 5, 7, 9) path 5 : includes segments (1, 3, 6, 9) Note 1: with just 2 paths ( Path 1 and Path 8) all the statements are covered. Note 2: with just 2 paths ( Path 1 and Path 8) all the branches are covered.

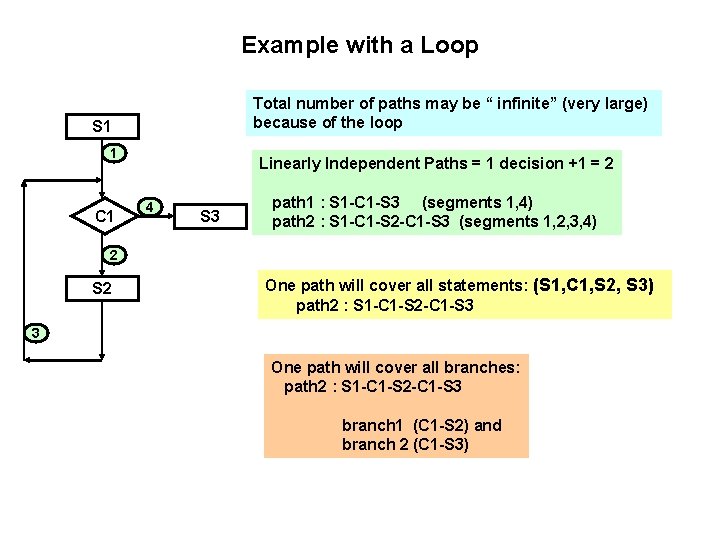
Example with a Loop Total number of paths may be “ infinite” (very large) because of the loop S 1 1 C 1 Linearly Independent Paths = 1 decision +1 = 2 4 S 3 path 1 : S 1 -C 1 -S 3 (segments 1, 4) path 2 : S 1 -C 1 -S 2 -C 1 -S 3 (segments 1, 2, 3, 4) 2 S 2 One path will cover all statements: (S 1, C 1, S 2, S 3) path 2 : S 1 -C 1 -S 2 -C 1 -S 3 3 One path will cover all branches: path 2 : S 1 -C 1 -S 2 -C 1 -S 3 branch 1 (C 1 -S 2) and branch 2 (C 1 -S 3)

More on Linearly Independent Paths • In discussing dimensionality, we talks about orthogonal vectors. – Two dimensional space has two orthogonal vector from which all the other vectors in two dimension can be obtained via “linear combination” of these vectors: • [1, 0] • [0, 1] [2, 4] [1, 0] [0, 1] e. g. [2, 4] = 2[1, 0] + 4[0, 1]

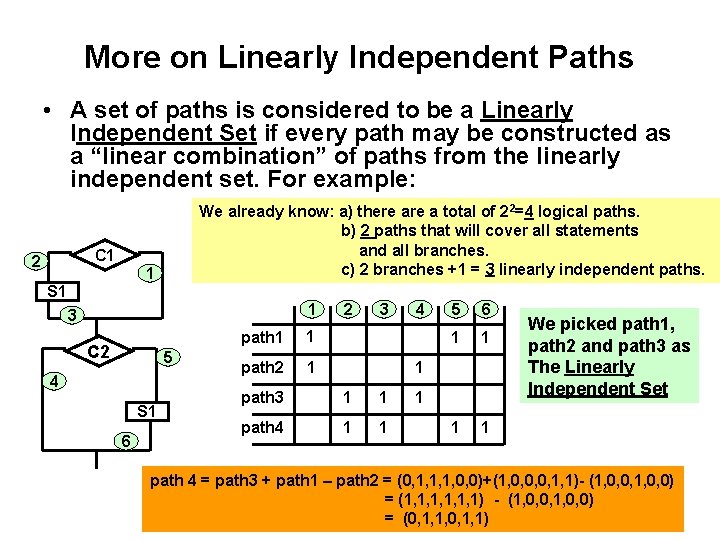
More on Linearly Independent Paths • A set of paths is considered to be a Linearly Independent Set if every path may be constructed as a “linear combination” of paths from the linearly independent set. For example: We already know: a) there a total of 22=4 logical paths. b) 2 paths that will cover all statements and all branches. c) 2 branches +1 = 3 linearly independent paths. C 1 2 1 S 1 1 3 C 2 5 4 S 1 6 path 1 1 path 2 1 2 3 4 5 6 1 1 1 path 3 1 1 path 4 1 1 1 We picked path 1, path 2 and path 3 as The Linearly Independent Set path 4 = path 3 + path 1 – path 2 = (0, 1, 1, 1, 0, 0)+(1, 0, 0, 0, 1, 1)- (1, 0, 0, 1, 0, 0) = (1, 1, 1, 1) - (1, 0, 0, 1, 0, 0) = (0, 1, 1, 0, 1, 1)

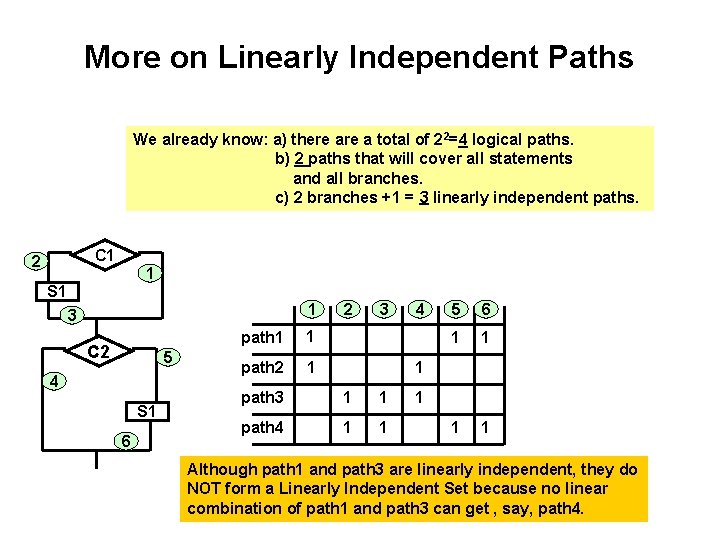
More on Linearly Independent Paths We already know: a) there a total of 22=4 logical paths. b) 2 paths that will cover all statements and all branches. c) 2 branches +1 = 3 linearly independent paths. C 1 2 1 S 1 1 3 C 2 5 4 S 1 6 path 1 1 path 2 1 2 3 4 5 6 1 1 1 path 3 1 1 path 4 1 1 1 Although path 1 and path 3 are linearly independent, they do NOT form a Linearly Independent Set because no linear combination of path 1 and path 3 can get , say, path 4.

More on Linearly Independent Paths • Because the Linearly Independent Set of paths display the same characteristics as the mathematical concept of basis in n-dimensional vector space, the testing using the Linearly Independent Set of paths is sometimes called the “basis” testing.

Paths Analysis • • Interested in Total number of “logical” paths Interested in Linearly Independent paths Interest in Branch coverage Interested in Statement coverage Which one is the largest set, next largest set, - - - , etc. ?