Max Flow Shortest Augmenting Path Algorithm Design by

Choosing Good Augmenting Paths Use care when selecting augmenting paths. Some choices lead to exponential algorithms. Clever choices lead to polynomial algorithms. If capacities are irrational, algorithm not guaranteed to terminate! n n n Goal: choose augmenting paths so that: Can find augmenting paths efficiently. Few iterations. n n Choose augmenting paths with: (Edmonds-Karp, 1972) Max bottleneck capacity. Sufficiently large capacity. Fewest number of edges. n n n 2

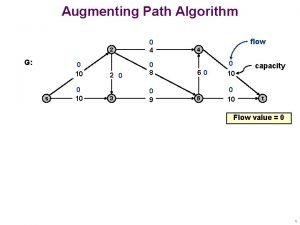
Shortest Augmenting Path Shortest augmenting path. Find augmenting path with fewest number of edges. BFS is an efficient implementation. n n may implement by accident! Shortest-Augmenting-Path(G, s, t, c) { foreach e E f(e) 0 Gf residual graph while (there exists an augmenting path) { find such a shortest such path P using BFS f Augment(f, c, P) update Gf } return f } 3

Shortest Augmenting Path: Overview of Analysis Proof outline. L 1. Throughout the algorithm, the length of the shortest path never proof ahead decreases. L 2. After at most m shortest path augmentations, the length of the proof ahead shortest augmenting path strictly increases. Theorem. The shortest augmenting path algorithm performs at most O(mn) augmentations. It can be implemented in O(m 2 n) time. O(m) time to find shortest augmenting path via BFS. O(m) augmentations for paths of exactly k edges. If there is an augmenting path, there is a simple one. 1 k<n O(mn) augmentations. ▪ n n n 4

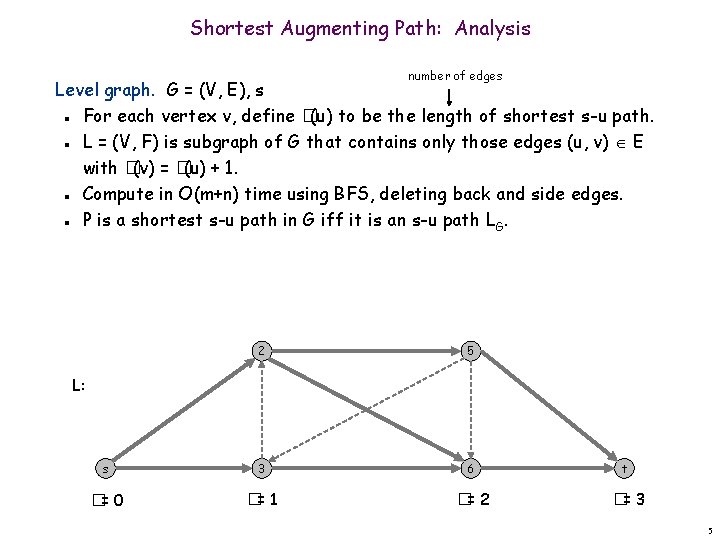
Shortest Augmenting Path: Analysis number of edges Level graph. G = (V, E), s For each vertex v, define � (u) to be the length of shortest s-u path. L = (V, F) is subgraph of G that contains only those edges (u, v) E with � (v) = � (u) + 1. Compute in O(m+n) time using BFS, deleting back and side edges. P is a shortest s-u path in G iff it is an s-u path LG. n n 2 5 s 3 6 �= 0 �= 1 �= 2 L: t �= 3 5

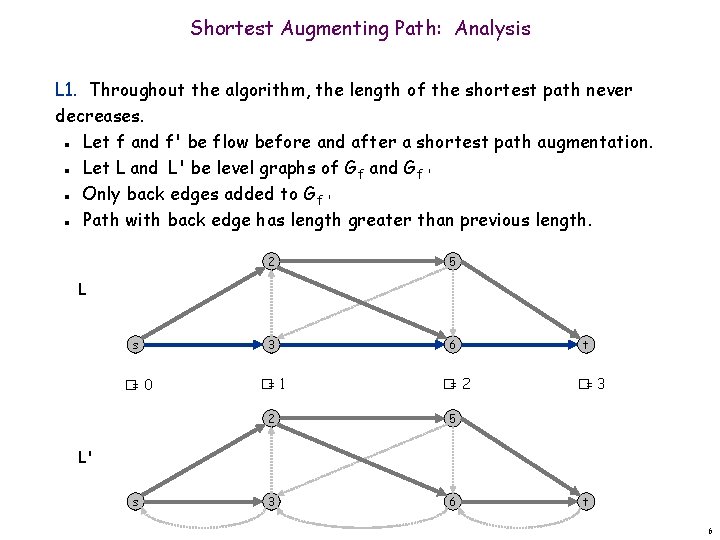
Shortest Augmenting Path: Analysis L 1. Throughout the algorithm, the length of the shortest path never decreases. Let f and f' be flow before and after a shortest path augmentation. Let L and L' be level graphs of Gf and Gf ' Only back edges added to Gf ' Path with back edge has length greater than previous length. n n 2 5 s 3 6 �= 0 �= 1 �= 2 2 5 3 6 L t �= 3 L' s t 6

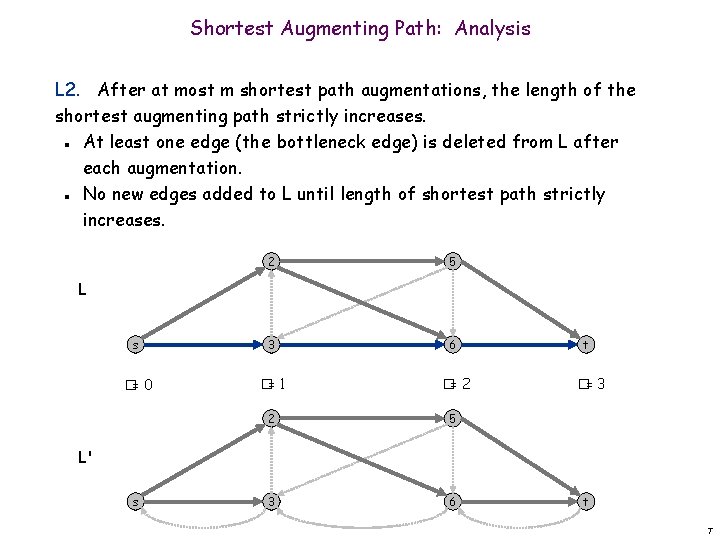
Shortest Augmenting Path: Analysis L 2. After at most m shortest path augmentations, the length of the shortest augmenting path strictly increases. At least one edge (the bottleneck edge) is deleted from L after each augmentation. No new edges added to L until length of shortest path strictly increases. n n 2 5 s 3 6 �= 0 �= 1 �= 2 2 5 3 6 L t �= 3 L' s t 7

Shortest Augmenting Path: Review of Analysis L 1. Throughout the algorithm, the length of the shortest path never decreases. L 2. After at most m shortest path augmentations, the length of the shortest augmenting path strictly increases. Theorem. The shortest augmenting path algorithm performs at most O(mn) augmentations. It can be implemented in O(m 2 n) time. Note: (mn) augmentations necessary on some networks. Try to decrease time per augmentation instead. Dynamic trees O(mn log n) Sleator-Tarjan, 1983 Simple idea O(mn 2) n n n 8

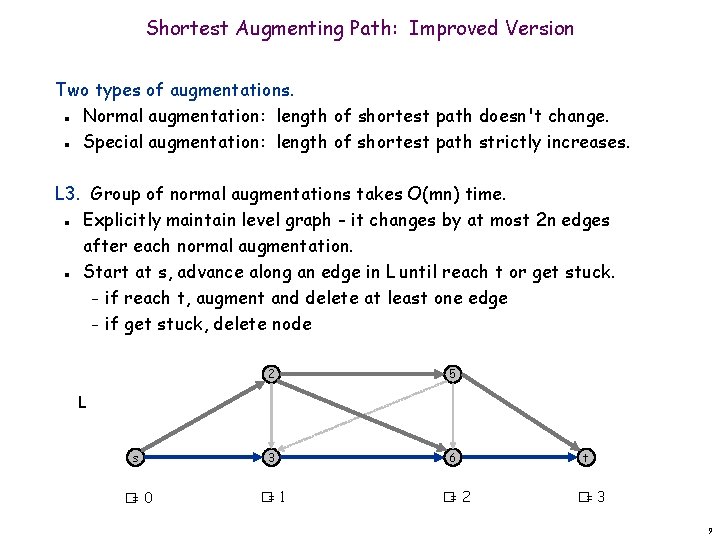
Shortest Augmenting Path: Improved Version Two types of augmentations. Normal augmentation: length of shortest path doesn't change. Special augmentation: length of shortest path strictly increases. n n L 3. Group of normal augmentations takes O(mn) time. Explicitly maintain level graph - it changes by at most 2 n edges after each normal augmentation. Start at s, advance along an edge in L until reach t or get stuck. – if reach t, augment and delete at least one edge – if get stuck, delete node n n 2 5 s 3 6 �= 0 �= 1 �= 2 L t �= 3 9

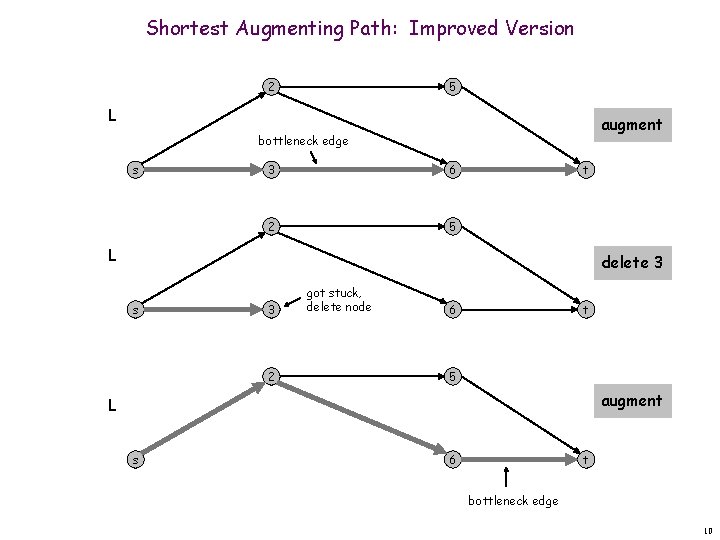
Shortest Augmenting Path: Improved Version 2 5 L augment bottleneck edge s 3 6 2 5 t L delete 3 s 3 2 got stuck, delete node 6 t 5 augment L s 6 t bottleneck edge 10

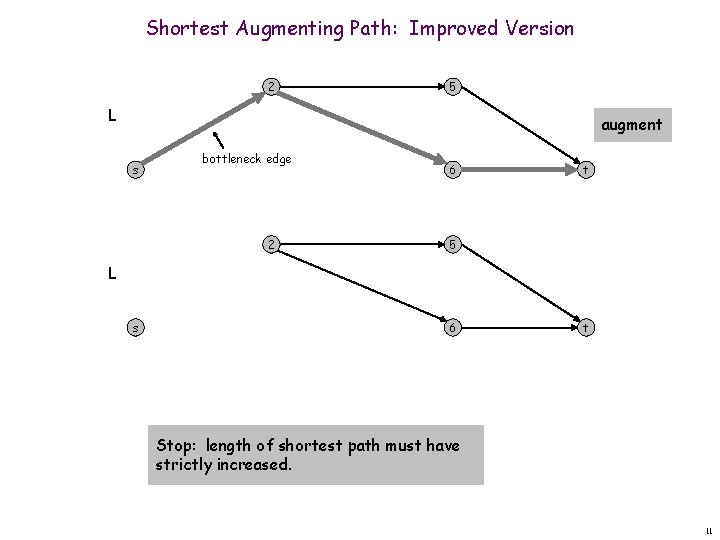
Shortest Augmenting Path: Improved Version 2 5 L augment s bottleneck edge 2 6 t 5 L s 6 t Stop: length of shortest path must have strictly increased. 11

Shortest Augmenting Path: Improved Version Advance-Retreat(V, E, f, s, t) { array pred[u V] L level graph of Gf u s, pred[v] nil repeat { while (there exists (u, v) L) { pred[v] u, u v advance if (u = t) { P path defined by pred[] f Augment(f, P) update L u s, pred[u] nil } } delete u from L retreat } until (u = s) return f } 12

Shortest Augmenting Path: Improved Version Two types of augmentations. Normal augmentation: length of shortest path doesn't change. Special augmentation: length of shortest path strictly increases. n n L 3. Group of normal augmentations takes O(mn) time. At most n advance steps before you either – get stuck: delete a node from level graph – reach t: augment and delete an edge from level graph n Theorem. Algorithm runs in O(mn 2) time. O(mn) time between special augmentations. At most n special augmentations. n n 13

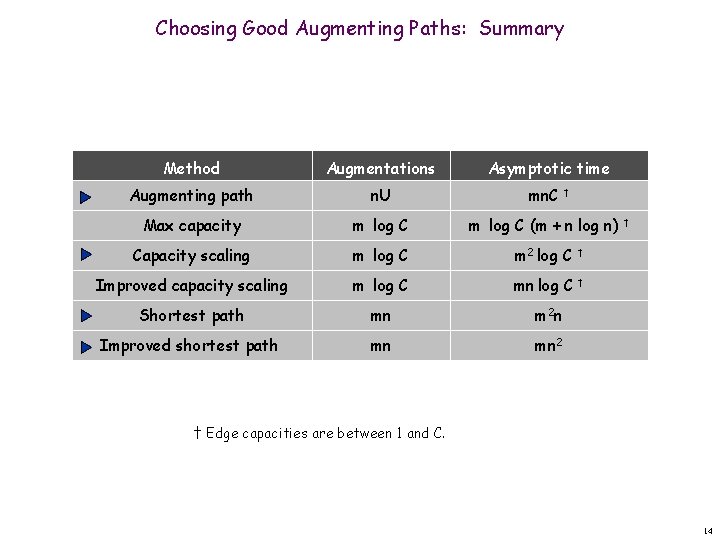
Choosing Good Augmenting Paths: Summary Method Augmentations Asymptotic time Augmenting path n. U mn. C Max capacity m log C (m + n log n) Capacity scaling m log C m 2 log C † Improved capacity scaling m log C mn log C † Shortest path mn m 2 n Improved shortest path mn mn 2 † † † Edge capacities are between 1 and C. 14

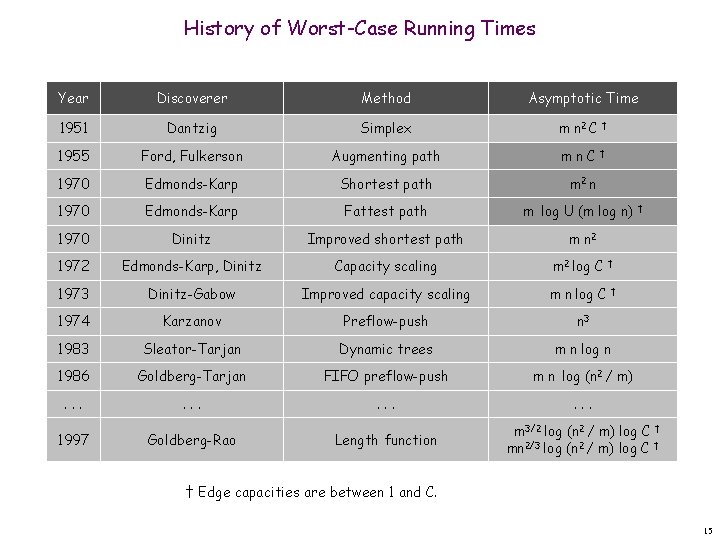
History of Worst-Case Running Times Year Discoverer Method Asymptotic Time 1951 Dantzig Simplex m n 2 C † 1955 Ford, Fulkerson Augmenting path 1970 Edmonds-Karp Shortest path 1970 Edmonds-Karp Fattest path 1970 Dinitz Improved shortest path 1972 Edmonds-Karp, Dinitz Capacity scaling m 2 log C 1973 Dinitz-Gabow Improved capacity scaling m n log C 1974 Karzanov Preflow-push n 3 1983 Sleator-Tarjan Dynamic trees m n log n 1986 Goldberg-Tarjan FIFO preflow-push m n log (n 2 / m) . . . 1997 Goldberg-Rao Length function m 3/2 log (n 2 / m) log C † mn 2/3 log (n 2 / m) log C † mn. C † m 2 n m log U (m log n) † m n 2 † † † Edge capacities are between 1 and C. 15

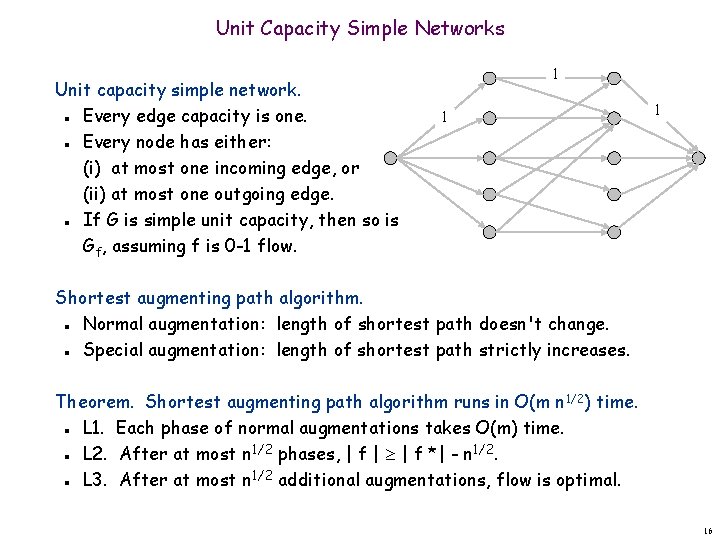
Unit Capacity Simple Networks Unit capacity simple network. Every edge capacity is one. Every node has either: (i) at most one incoming edge, or (ii) at most one outgoing edge. If G is simple unit capacity, then so is Gf, assuming f is 0 -1 flow. n 1 1 1 n n Shortest augmenting path algorithm. Normal augmentation: length of shortest path doesn't change. Special augmentation: length of shortest path strictly increases. n n Theorem. Shortest augmenting path algorithm runs in O(m n 1/2) time. L 1. Each phase of normal augmentations takes O(m) time. L 2. After at most n 1/2 phases, | f | | f *| - n 1/2. L 3. After at most n 1/2 additional augmentations, flow is optimal. n n n 16

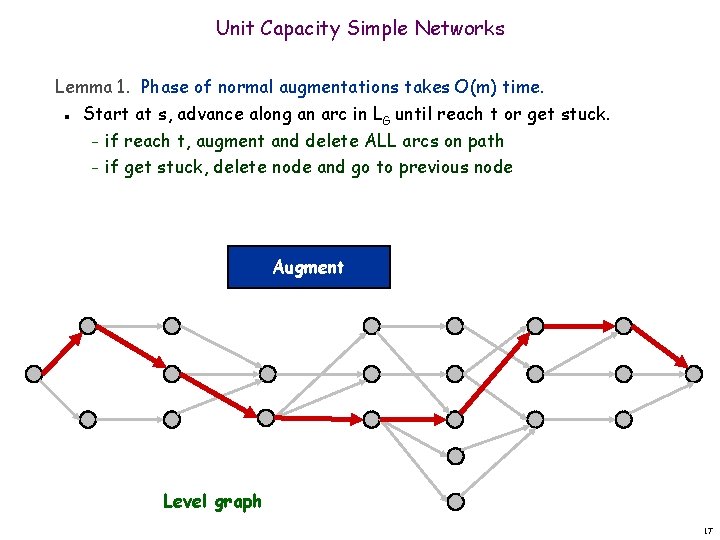
Unit Capacity Simple Networks Lemma 1. Phase of normal augmentations takes O(m) time. n Start at s, advance along an arc in LG until reach t or get stuck. – if reach t, augment and delete ALL arcs on path – if get stuck, delete node and go to previous node Augment Level graph 17

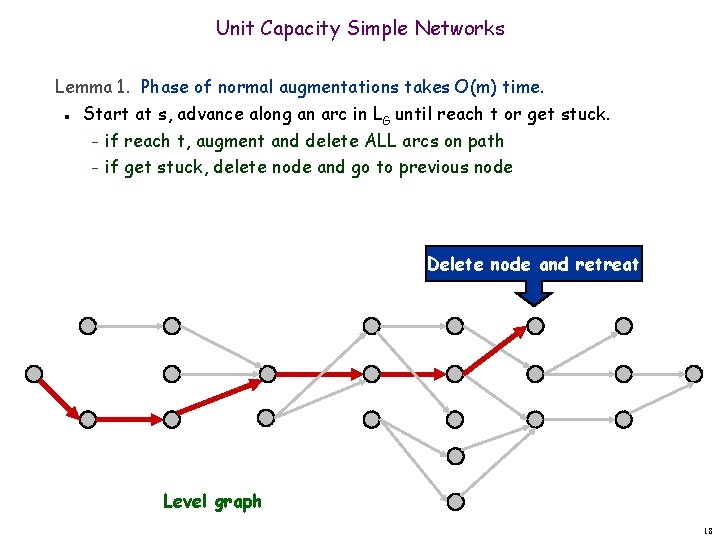
Unit Capacity Simple Networks Lemma 1. Phase of normal augmentations takes O(m) time. n Start at s, advance along an arc in LG until reach t or get stuck. – if reach t, augment and delete ALL arcs on path – if get stuck, delete node and go to previous node Delete node and retreat Level graph 18

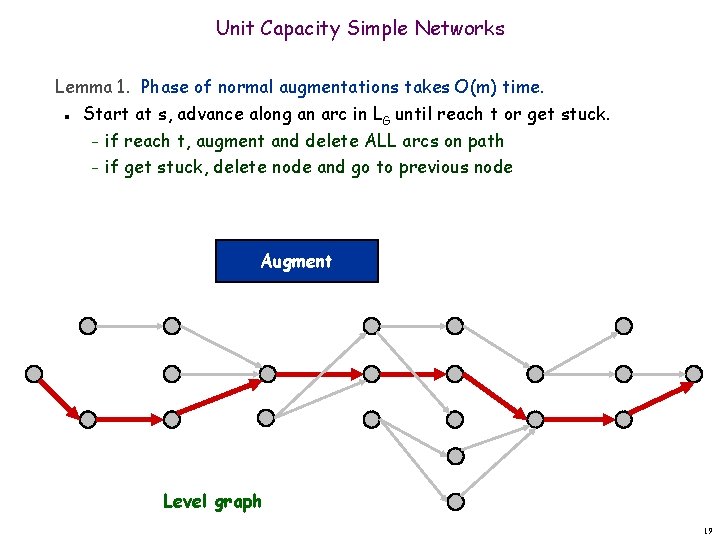
Unit Capacity Simple Networks Lemma 1. Phase of normal augmentations takes O(m) time. n Start at s, advance along an arc in LG until reach t or get stuck. – if reach t, augment and delete ALL arcs on path – if get stuck, delete node and go to previous node Augment Level graph 19

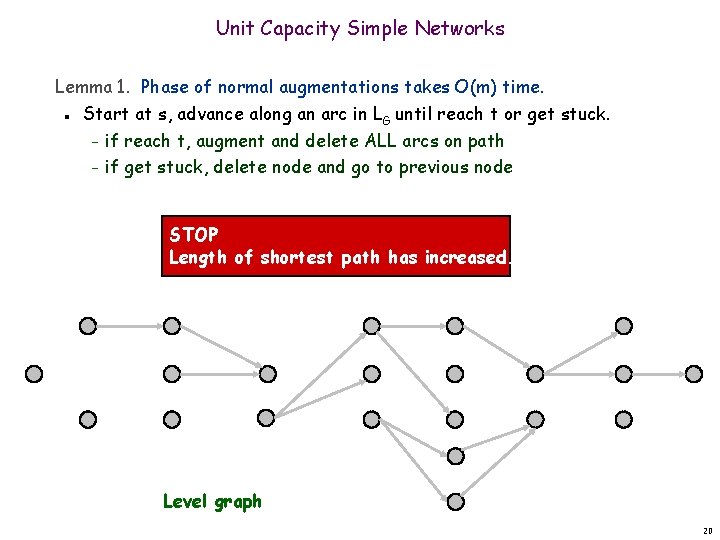
Unit Capacity Simple Networks Lemma 1. Phase of normal augmentations takes O(m) time. n Start at s, advance along an arc in LG until reach t or get stuck. – if reach t, augment and delete ALL arcs on path – if get stuck, delete node and go to previous node STOP Length of shortest path has increased. Level graph 20

Unit Capacity Simple Networks Lemma 1. Phase of normal augmentations takes O(m) time. Start at s, advance along an arc in LG until reach t or get stuck. – if reach t, augment and delete ALL arcs on path – if get stuck, delete node and go to previous node n n O(m) running time. – O(m) to create level graph – O(1) per arc, since each arc traversed at most once – O(1) per node deletion 21

Unit Capacity Simple Networks Advance. Retreat(V, E, f, s, t) ARRAY pred[v V] LG level graph of Gf v s, pred[v] nil REPEAT WHILE (there exists (v, w) LG) pred[w] v, v w IF (v = t) P path defined by pred[] f augment(f, P) update LG v s, pred[v] nil delete v from LG UNTIL (v = s) advance augment retreat RETURN f 22

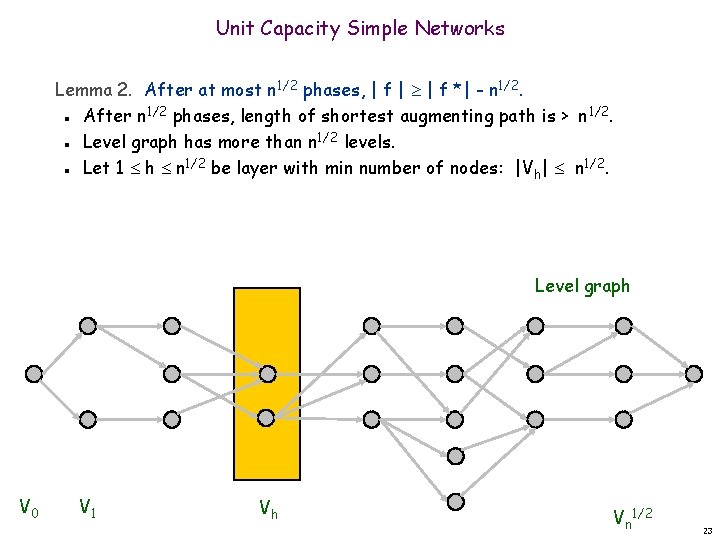
Unit Capacity Simple Networks Lemma 2. After at most n 1/2 phases, | f | | f *| - n 1/2. After n 1/2 phases, length of shortest augmenting path is > n 1/2. Level graph has more than n 1/2 levels. Let 1 h n 1/2 be layer with min number of nodes: |Vh| n 1/2. n n n Level graph V 0 V 1 Vh Vn 1/2 23

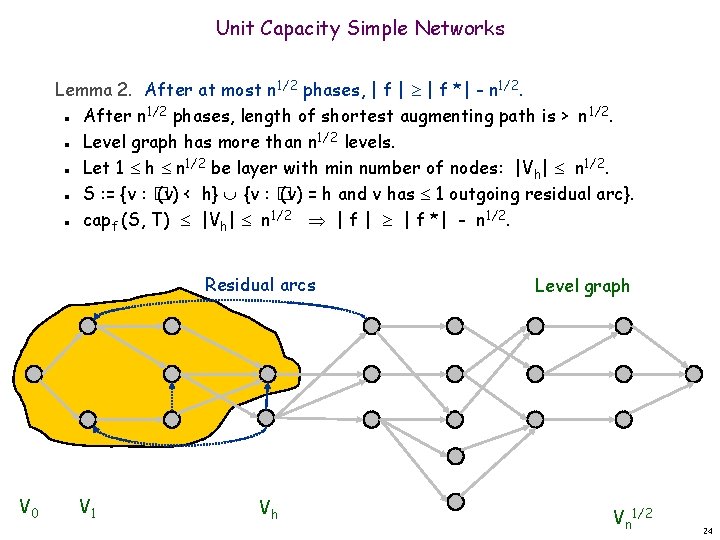
Unit Capacity Simple Networks Lemma 2. After at most n 1/2 phases, | f | | f *| - n 1/2. After n 1/2 phases, length of shortest augmenting path is > n 1/2. Level graph has more than n 1/2 levels. Let 1 h n 1/2 be layer with min number of nodes: |Vh| n 1/2. S : = {v : � (v) < h} {v : � (v) = h and v has 1 outgoing residual arc}. capf (S, T) |Vh| n 1/2 | f | | f *| - n 1/2. n n n Residual arcs V 0 V 1 Vh Level graph Vn 1/2 24