Modle linaire Analyse numrique dune matrice de corrlation

Modèle linéaire. Analyse numérique d’une matrice de corrélation. Transitivité et Colinéarité. Thierry Foucart UMR 6086, Mathématiques, SP 2 MI, Bd Marie et Pierre Curie, BP 30179 86962 FUTUROSCOPE CHASSENEUIL CEDEX.

1. introduction au modèle linéaire.

1. 1 un exemple • étude des liaisons entre le revenu, l’âge, la CSP, le niveau de diplôme, l’orientation politique, le sexe … au sein d’une population d’électeurs. • Grand nombre de tableaux croisés : impuissance des tests classiques du c 2 et de Fisher • modélisation : expression mathématique des liaisons.

1. 2 modèle linéaire. Y = b 0 + b 1 X 1 + b 2 X 2 + b 3 X 3 + b 4 X 4 + Y : revenu X 1 : âge X 2 : CSP X 3 : diplôme X 4 : orientation politique : variable d’ajustement hypothèses rigides (linéarité, indépendance des observations, normalité et homoscédasticité de la variable d’ajustement ).

1. 3 interprétation du modèle • toutes choses égales par ailleurs. • recherche d’un effet propre de Xj sur Y : bj 0. • l’âge X 1 augmente d’un an : le revenu moyen Y augmente toujours de b 1, quelle que soient la CSP, le diplôme, l’orientation politique. • démarche implicite : on suppose a priori l’existence d’un effet propre et on le contrôle.

1. 4 analyse en quatre points : • Analyse numérique de la matrice des corrélations : transitivité, corrélation partielle. • Colinéarité : instabilité des estimations • Evaluation de la régression bornée. • Régression orthogonale. Sélection des composantes principales.

2. Analyse numérique d’une matrice de corrélation

2. 1 Modèle linéaire. Y = b 0 + b 1 X 1 + … + bj Xj +. . . + bp Xp + E(Xj) = 0, V(Xj) = 1 bj = coefficients de régression théoriques : variable résiduelle : E( ) = 0, V( ) = 2 X : matrice des observations des Xj (en colonnes) Y : matrice des observations de Y (en colonne) R : matrice symétrique p x p des corrélations entre les variables Xj

2. 2 Estimateur MCO B : estimateur sans biais de variance minimale (efficace) défini par (B 1, B 2, . . . , Bp)t. Bj : estimateur du coefficient bj Les propriétés des estimateurs dépendent de R-1

2. 3. Factorisation de Cholesky. Le calcul de R-1 consiste à factoriser R puis à inverser T. R = T T t Factorisation de Cholesky L T matrice triangulaire supérieure La matrice R étant symétrique définie positive est inversible : la matrice T existe et est inversible.

2. 4 Calcul de la matrice T " i = 1, . . . , p ti, 1 = r 1, i / [r 1, 1 ] ½ (1) "i = 2, . . . , p i-1 ti, i = [ri, i - ti, k 2 ]1/2 k=1 (2) "i=2, . . . , p-1 "j=i+1, . . . p i-1 ri, j - ti, k tj, k k = 1 tj, i = __________ ti, i (3)

2. 5 Encadrement d’un terme -1 ap, p– 1< rp, p– 1 < bp, p-1 1 p-2 ap, p– 1 = – tp– 1, p– 1 [1 – tp, k 2]1/2 + tp– 1, k tp, k k = 1 p-2 bp, p– 1 = tp– 1, p– 1 [1 – tp, k 2]1/2 + tp– 1, k tp, k k = 1 généralisation par permutation ai, j < ri, j < bi, j

2. 6 terme diagonal p-1 cp, p = tp, k 2 k = 1 rp, p > cp, p rj, j > cj, j = Rj 2 : coefficient de détermination obtenu dans la régression de Xj par les autres variables explicatives

2. 6 Exemple numérique X 1 X 2 X 3 X 4 X 1 1 0. 5 -0. 5 X 2 X 3 X 4 1 0. 5 1 0. 4 0. 3 1 r 1, 2 ] -0. 3697771 , 0. 5126343 [ r 4, 4 ]. 98 , + [ R 42 = 0. 98

3. Relations entre les corrélations

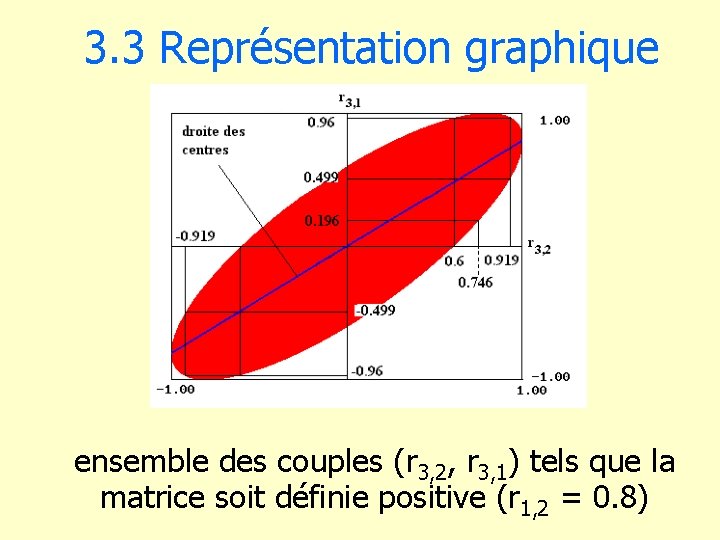
3. 1 Transitivité de la corrélation. X Y Z X 1 R = Y 0. 8 1 Z r 3, 1 r 3, 2 1 • Forte corrélation entre X et Y : r 1, 2 = 0. 8 • Une forte corrélation entre Y et Z (r 3, 2 = 0. 8) implique-t-elle une forte corrélation entre X et Z (r 3, 1 élevé) ?

3. 2 Evaluation de la transitivité X Y Z X 1 R = Y 0. 8 1 Z r 3, 1 r 3, 2 1 • • r 3, 2 = -0. 2 r 3, 2 = 0. 6 r 3, 2 = 0. 746 r 3, 2 = 0. 919 r 3, 1 ]-0. 75, 0. 43[ r 3, 1 ] 0, 0. 96 [ r 3, 1 ] 0. 196, 1[ (>>0 pour n=100) r 3, 1 ] 0. 499, 1[

3. 3 Représentation graphique ensemble des couples (r 3, 2, r 3, 1) tels que la matrice soit définie positive (r 1, 2 = 0. 8)

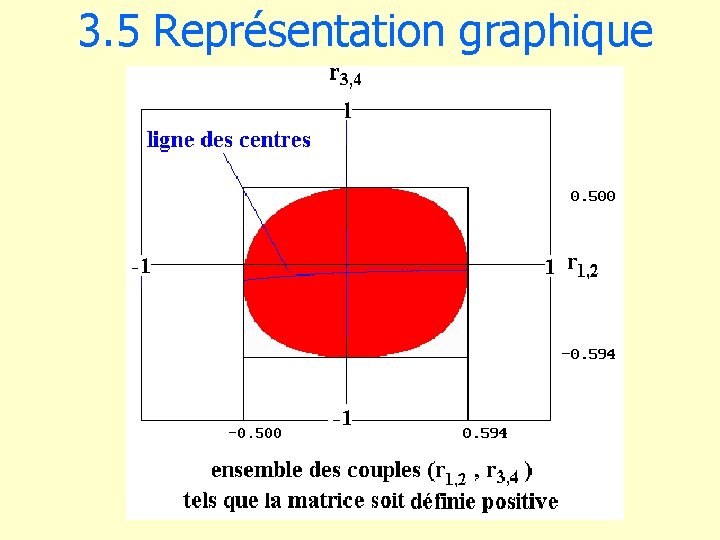
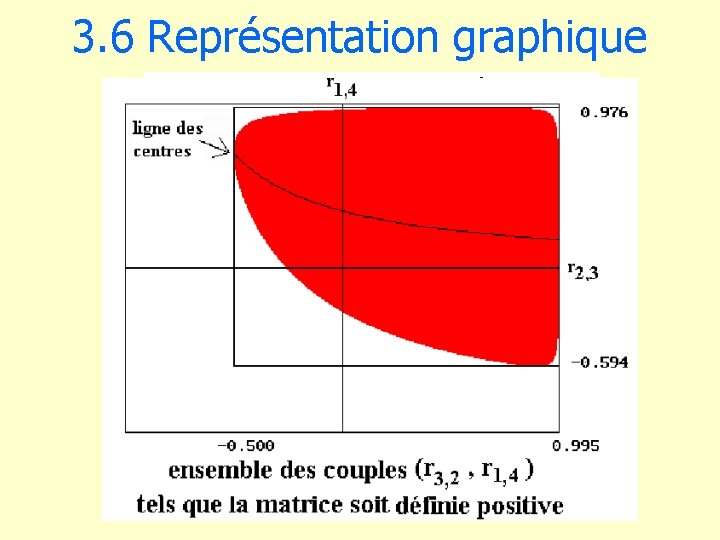
3. 4 Généralisation • cas d’une matrice p x p : X 1 X 2 X 3 X 4 X 1 1 X 2 0. 5 1 X 3 0. 5 1 X 4 -0. 5 0. 4 0. 3 1 • relation entre r 1, 2 et r 3, 4 : quelle est la conséquence de la liaison entre la CSP et le diplôme (r 1, 2) sur la liaison entre l’âge et le revenu (r 3, 4) ?

3. 5 Représentation graphique

3. 6 Représentation graphique

3. 7 Positionnement du coefficient de corrélation Evaluation de la position de ri, j dans son intervalle ] a, b [ à l’aide d’un indice variant de – 1 à 1 - 1 (ri, j – (a+b)/2) / [ (b – a)/2 ] 1

3. 8 corrélation partielle On obtient le coefficient de corrélation partielle : rpi, j = (ri, j – (a+b)/2) / [ (b – a)/2 ] • ri, j = (a + b)/2 si et seulement si rpi, j = 0 • rpi, j fonction linéaire croissante de ri, j • ri, j tend vers a ou b si et seulement rpi, j tend vers 1 en v. a. • relation entre rk, l et rpi, j : rk, l tend vers a (ou b) implique rpi, j tend vers 1 en v. a. (sous conditions)

4. Colinéarités statistiques.

4. 1 Application du modèle • Domaine d’application D = ensemble des valeurs vraisemblables des variables explicatives. • forte liaison entre la CSP et le diplôme : un employé a rarement un diplôme BAC+5. Le modèle ne permet pas d’estimer le revenu d’un employé titulaire d’un BAC+5. • Plus les variables explicatives sont nombreuses : 1. plus le risque de colinéarité est élevé. 2. moins la colinéarité est visible. 3. plus le domaine d’application est restreint.

4. 2 Colinéarités statistiques • entre deux variables : leur coefficient de corrélation linéaire est proche de 1 en valeur absolue. • entre plusieurs variables : il existe une combinaison linéaire de ces variables de variance faible (d’où l’ACP).

4. 3 Conséquences numériques Les termes de la matrice R-1 sont élevés, en particulier les termes diagonaux. Termes diagonaux de VB : variances des estimateurs Bj

4. 4 Effets de la colinéarité statistique • Variances des estimateurs MCO des bj élevées : d’où valeurs des coefficients estimés parfois élevées. • Coefficients de corrélation entre les Bj proches de 1 : compensation entre les estimations • Conséquence : coefficients estimés parfois opposés aux coefficients théoriques • Coefficient de détermination instable.

4. 5 modèle simulé. Y = 0. 5 X 1 + 0. 5 X 2 – 0. 5 X 3 – 0. 5 X 4 + n = 100 R X 1 X 2 X 3 X 4 X 1 1 X 2 0. 5 1 X 3 0. 5 1 X 4 -0. 5 0. 4 0. 3 1 2 = 1

4. 6 Interprétation du modèle : Le modèle théorique correspond aux propriétés suivantes : • l’âge et la CSP ont un effet propre positif sur le revenu (b 1 = b 2 = 0. 5 ) • le diplôme et l’orientation politique un effet propre négatif sur le revenu (b 3 = b 4 = - 0. 5 ).

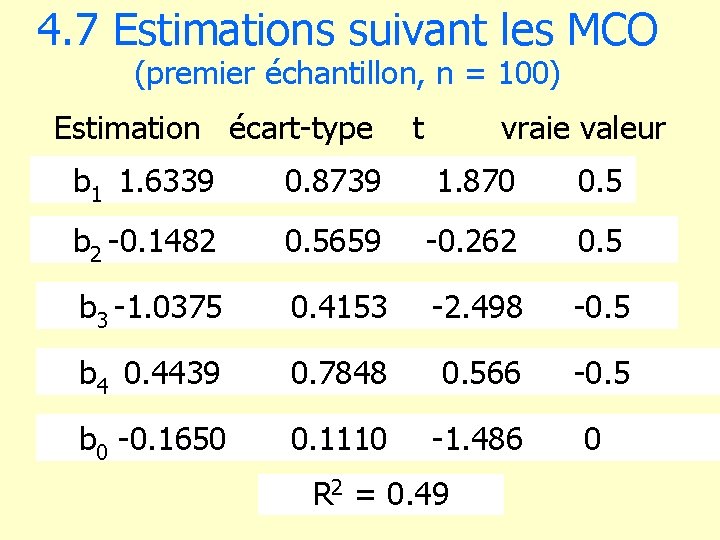
4. 7 Estimations suivant les MCO (premier échantillon, n = 100) Estimation écart-type t vraie valeur b 1 1. 6339 0. 8739 1. 870 0. 5 b 2 -0. 1482 0. 5659 -0. 262 0. 5 b 3 -1. 0375 0. 4153 -2. 498 -0. 5 b 4 0. 4439 0. 7848 0. 566 -0. 5 b 0 -0. 1650 0. 1110 -1. 486 0 R 2 = 0. 49

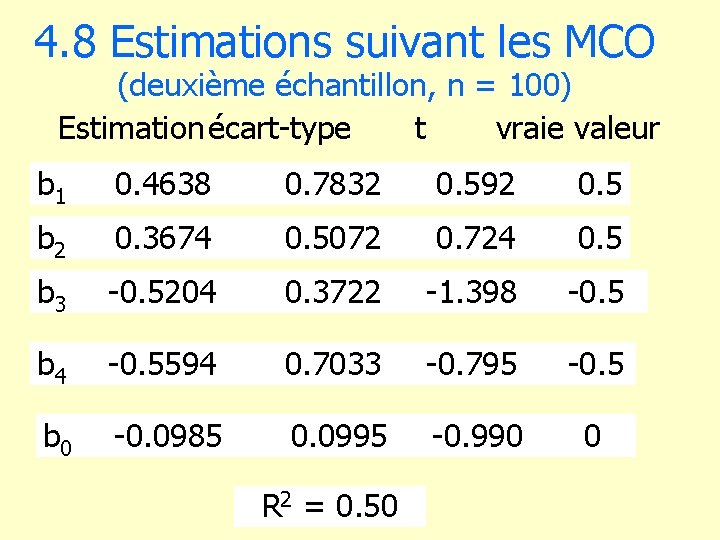
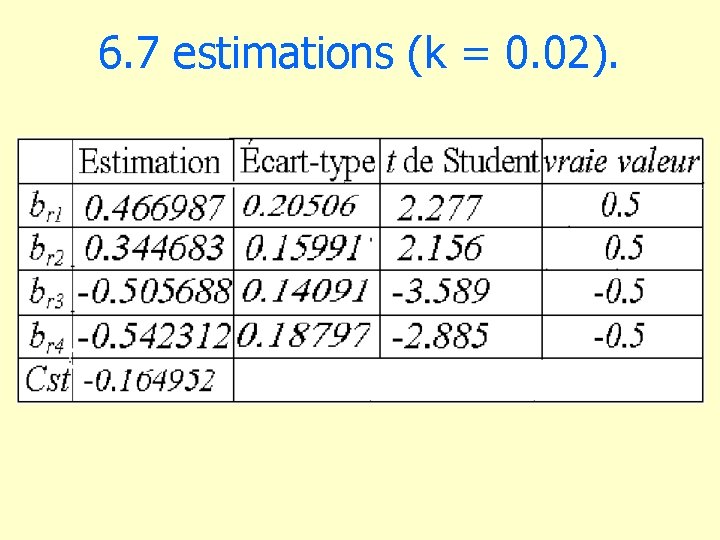
4. 8 Estimations suivant les MCO (deuxième échantillon, n = 100) Estimationécart-type t vraie valeur b 1 0. 4638 0. 7832 b 2 0. 3674 0. 5072 0. 724 0. 5 b 3 -0. 5204 0. 3722 -1. 398 -0. 5 b 4 -0. 5594 0. 7033 -0. 795 -0. 5 b 0 -0. 0985 0. 0995 -0. 990 0 R 2 = 0. 50 0. 592 0. 5

4. 9 Coefficient de détermination Troisième exemple X 1 X 2 X 3 X 1 1 X 2 0. 6 1 X 3 -0. 279 0. 6 Y Y 0. 0446 0 0 1 1 R 2 = 0. 99536 (r 1, 2 = 0. 600) R 2 = 0. 45260 (r 1, 2 = 0. 599)

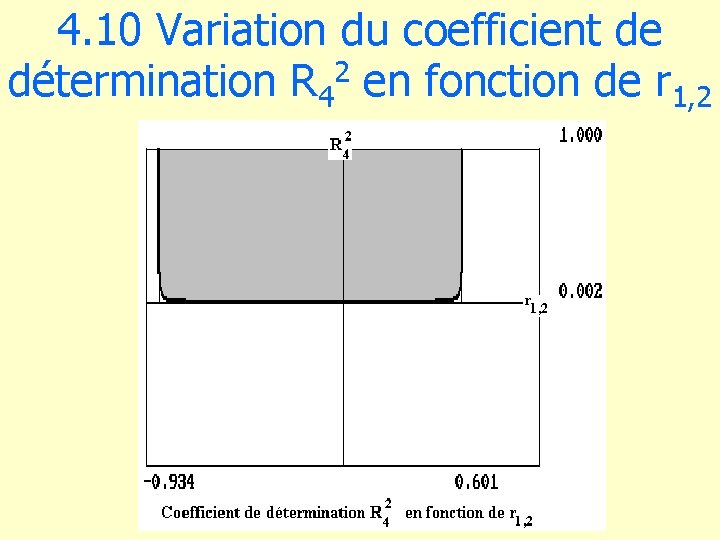
4. 10 Variation du coefficient de détermination R 42 en fonction de r 1, 2

5. Détection de la colinéarité. X 1 X 2 X 3 X 4 X 1 1 0. 5 -0. 5 X 2 X 3 X 4 1 0. 5 1 0. 4 0. 3 1

5. 1 Facteurs d’inflation • Facteurs d’inflation : fj = 1 / (1 – Rj 2) (termes diagonaux de la matrice R-1) • Indice de multicolinéarité (Tomassonne) : I = (1/p) � fj (moyenne des facteurs d’inflation) En l’absence totale de colinéarité, les facteurs d’inflation et l’indice I sont égaux à 1

5. 2 Valeurs propres • On note 1, 2, …, p les valeurs propres de R classées suivant les valeurs décroissantes. Faibles valeurs propres : colinéarité statistique • L’indice de conditionnement (Belsley et al. ): = 1/ p (ou 1/ p) • L’indice de multicolinéarité : I = (1/p) � 1/ j

5. 3 Application au modèle simulé • Facteurs d’inflation : b 1 f 1 = b 2 f 2 = b 3 f 3 = b 4 f 4 = 62 26 14 50 • Valeurs propres 1=2. 019 2=1. 47 3=0. 5 4= 0. 007 • Indice de multicolinéarité I = 38 • Indice de conditionnement = 148. 83

6. Application de la régression bornée.

6. 1 Estimateur biaisé d’un paramètre m E[(X’ – m )2] = V(X’) + [E(X’) – m]2 E[(X – m )2] = V(X) > E[(X’ – m )2]

6. 2 Estimateur de la régression bornée critère des MC sous la contrainte B 2 M (Pour k = 0, on retrouve l’estimateur des MCO)

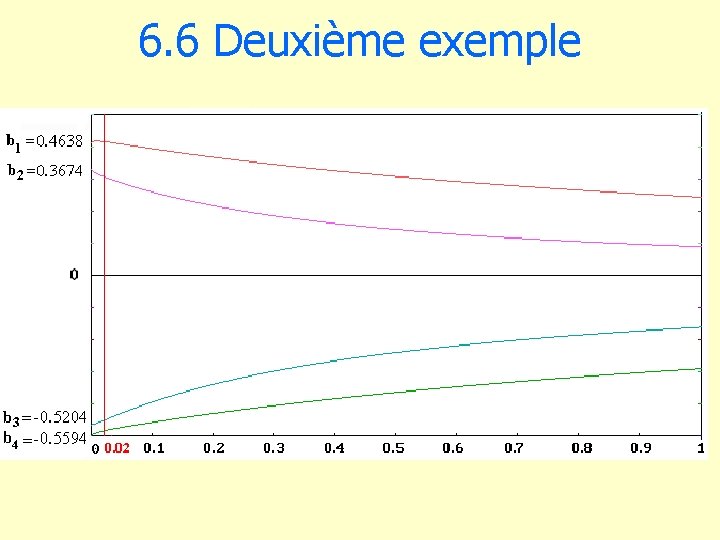
6. 3 Application. • On fait varier k de 0 à 1. • on estime les coefficients de régression par l’estimateur de la régression bornée. • On construit la représentation graphique des bj en fonction de k appelée ridge trace. • On choisit k de façon que leurs valeurs soient stabilisées.

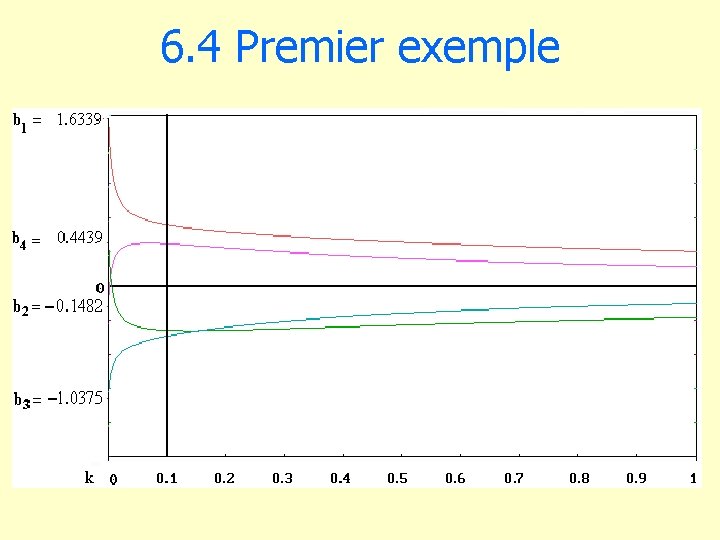
6. 4 Premier exemple

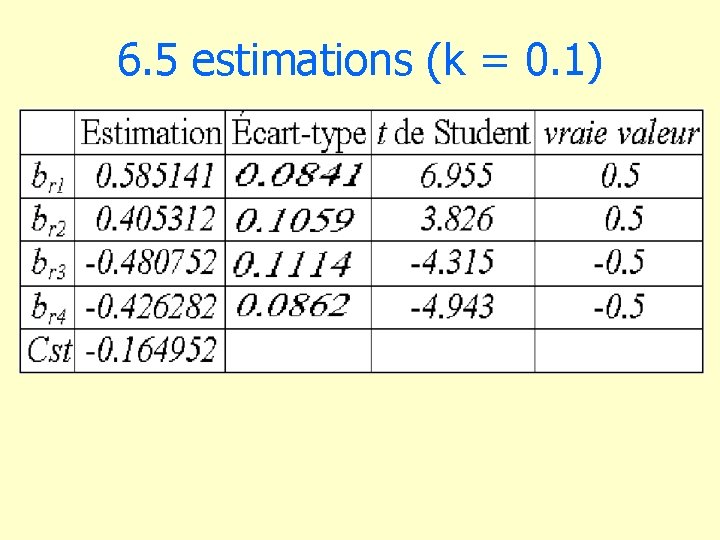
6. 5 estimations (k = 0. 1)

6. 6 Deuxième exemple

6. 7 estimations (k = 0. 02).

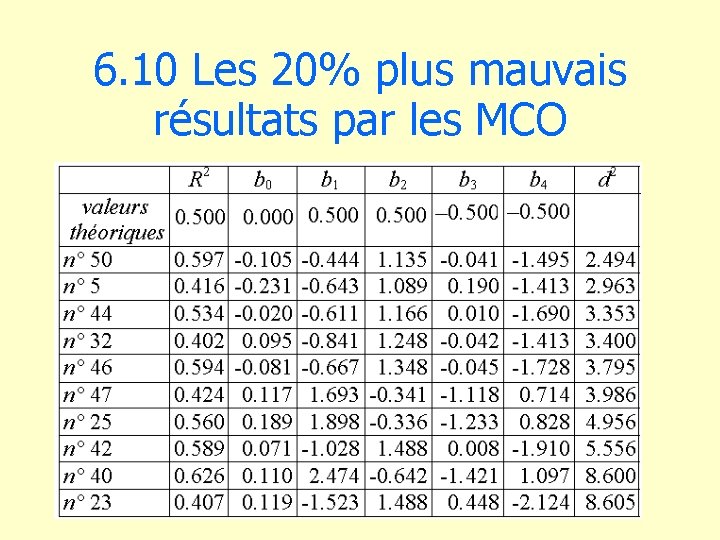
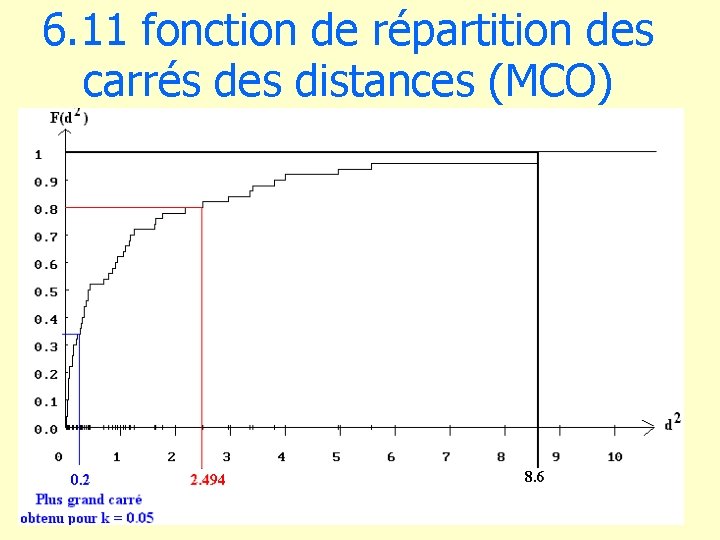
6. 8 Distances entre vecteur observé et vecteur réel d b��, B = bj – bj (erreur quadratique) • 50 échantillons de taille 100 : 50 distances 1) par la régression des MCO k = 0 2) par la régression bornée k = 0. 01 3) par la régression bornée k = 0. 05

6. 9 Résultats numériques Carrés des distances entre vecteurs estimés et vecteur vrai (50 vecteurs estimés)

6. 10 Les 20% plus mauvais résultats par les MCO

6. 11 fonction de répartition des carrés des distances (MCO)

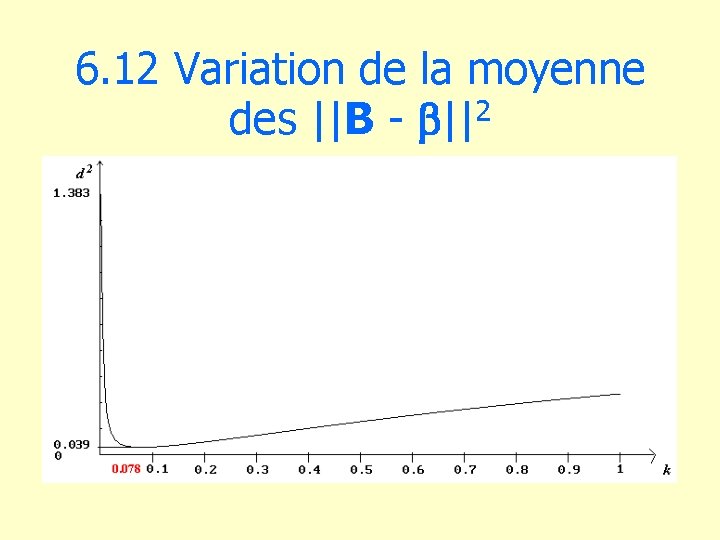
6. 12 Variation de la moyenne des ||B - b||2

6. 13 Optimisation Meilleure Moyenne des Variance valeur de k : carrés des distances k = 0. 078 0. 039 0. 001 Forte stabilité de l’erreur quadratique pour 0. 05 < k < 0. 1

6. 14 Critique de la régression bornée • amélioration considérable des estimations • résultats discutables dans le cas de coefficients de régression théoriques élevés en valeur absolue. D’où la nécessité de les évaluer a priori. • mise en oeuvre nécessitant une démarche critique d’analyse des coefficients de régression.

6. 15 Développements • Régression bornée partielle : on calcule les dérivées des coefficients de régression par rapport à chaque terme diagonal de R, et on on ajoute une constante à ceux dont la dérivée est la plus grande en v. a. • Détection de valeurs influentes : les valeurs observées influentes sont celles par rapport auxquelles dérivées des coefficients de régression sont les plus grandes en v. a.

7. régression orthogonale

7. 1 Méthode ACP du tableau de données X : C=XU • U : tableau des vecteurs principaux, vecteurs propres unitaires de R. • C : tableau des composantes principales Cl (n lignes et q colonnes) On considère les composantes principales comme variables explicatives.

7. 2 Modélisation et estimateurs Y = b 0’ + b 1’ C 1 + … + bl’ Cl +. . . + bp’ Cp + bl’ = cov (Y, Cl) / l B’ = 1/n D 1/ Ct Y estimateur B’’ des coefficients de régression des variables initiales : B’’ = U B’ VB’’ = U VB’ Ut

7. 3 Choix des composantes principales Algorithme descendant On sélectionne la composante principale Cl en fonction de son coefficient de régression bl’ avec la variable expliquée Y. • bl’ > b’ 0 : on sélectionne la composante principale. • bl’ < b’ 0 : on écarte la composante principale. Le test sur le coefficient de corrélation partielle rpl est équivalent : on fixe alors une valeur limite rp 0.

7. 4 Premier type d’erreur Y = b 0’ + b 1’ C 1 + … + bl’ Cl +. . . + bp’ Cp + (théo. ) Y = b 0’ + b 1’ C 1 + … + bl’ Cl +. . . + bp’ Cp + e (obs. ) erreur possible : introduire Cl avec bl’ nul : la moyenne des carrés des erreurs est égale à : bl’ 2 l (erreur de type I)

7. 5 Second type d’erreur Y = b 0’ + b 1’ C 1 + … + bl’ Cl +. . . + bp’ Cp + (théo. ) Y = b 0’ + b 1’ C 1 + … + bl’ Cl +. . . + bp’ Cp + e (obs. ) erreur possible : éliminer Cl avec bl’ non nul (erreur de type II) La moyenne des carrés des erreurs est égale à bl’ 2 l

7. 6 évaluation de l’erreur de type II: • bl’ inconnu : Démarche baysienne • Probabilité a priori sur l’ensemble contenant le coefficient de régression bl’ • E(bl’ 2 l ) : mesure de l’erreur de type II. • En pratique : on étudie le coefficient de corrélation partielle (loi normale tronquée).

7. 7 Algorithme • On choisit la région critique du test en fixant un coefficient de corrélation partielle limite. • On calcule la somme des deux erreurs • On recommence le calcul en faisant varier le coefficient de corrélation partielle limite de -1 à 1. • on en déduit celui qui minimise la moyenne des deux erreurs. On applique cet algorithme aux deux exemples précédents.

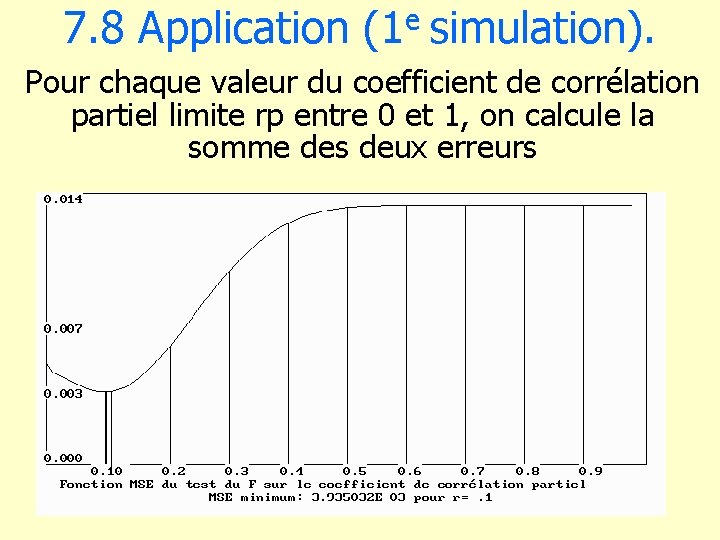
7. 8 Application (1 e simulation). Pour chaque valeur du coefficient de corrélation partiel limite rp entre 0 et 1, on calcule la somme des deux erreurs

7. 9 Résultats numériques Valeur limite du coefficient de corrélation partielle 0. 0991 Valeur du coefficient de corrélation correspondant 0. 0709 Valeur limite du F 0. 9422 vraisemblance P(F>f)= 0. 3389

7. 10 Exemple 1 : conclusion • toutes les composantes principales sont conservées. • les coefficients de régresion sont égaux coefficients de régression initiaux (MC). • la régression bornée et la régression orthogonale donnent des résultats très différents. • D’où la nécessité d’une réflexion a priori sur les coefficients de régression théoriques.

e 7. 11 Application (2 simulation). • Valeur limite 0. 149, observée 0. 002. On élimine C 4. • On élimine également C 1, et les prédicteurs retenus sont C 2 et C 3 (variance résiduelle estimée minimale).

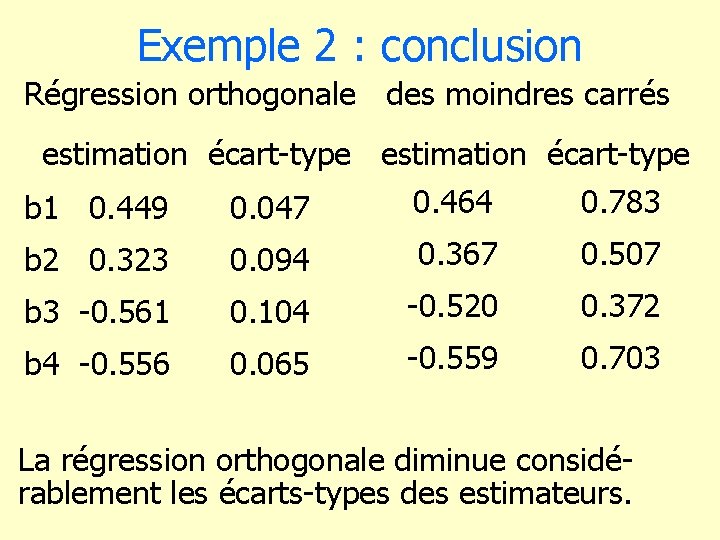
Exemple 2 : conclusion Régression orthogonale des moindres carrés estimation écart-type 0. 464 0. 783 b 1 0. 449 0. 047 b 2 0. 323 0. 094 0. 367 0. 507 b 3 -0. 561 0. 104 -0. 520 0. 372 b 4 -0. 556 0. 065 -0. 559 0. 703 La régression orthogonale diminue considérablement les écarts-types des estimateurs.

7. 13 Commentaires sur l’algorithme • Le choix des composantes principales à éliminer dépend de [r(Y, Cl) 2 / l ]. • Eliminer une composante principale de faible variance n’est pas toujours une bonne décision. • Conserver une composante principale de variance relativement élevée n’est pas toujours une bonne décision. • Risque de 1 e espèce correspondant à la valeur limite largement supérieur à 5%.

CONCLUSION • Le modèle linéaire compense l’impuissance des tests classiques en recourant à des hypothèses rigides. • Ces hypothèses mathématiques sont vérifiées dans les simulations effectuées, mais jamais dans la réalité. • Une réflexion non statistique sur la nature des données est indispensable pour appliquer le modèle linéaire et en interpréter correctement les résultats.

BIBLIOGRAPHIE 1. Colinéarité et régression linéaire, Math. & Sci. hum. Mathematics and Social Sciences (43 e année, n° 173, 2005(4), p. 5 -25). 2. évaluation de la régression bornée. Revue des Nouvelles Technologies de l’Information, éd. Cépaduès sous presse. 3. Limites de l’informatisation des sciences de l’homme et de la société. Contribution à l’ouvrage collectif Les sciences humaines et sociales à l’heure des technologies de l’information et de la communication, dir. B. Reber C. Brossaud , publication prévue juin 2007, Hermès, Paris.

Compléments http: //foucart. thierry. free. fr

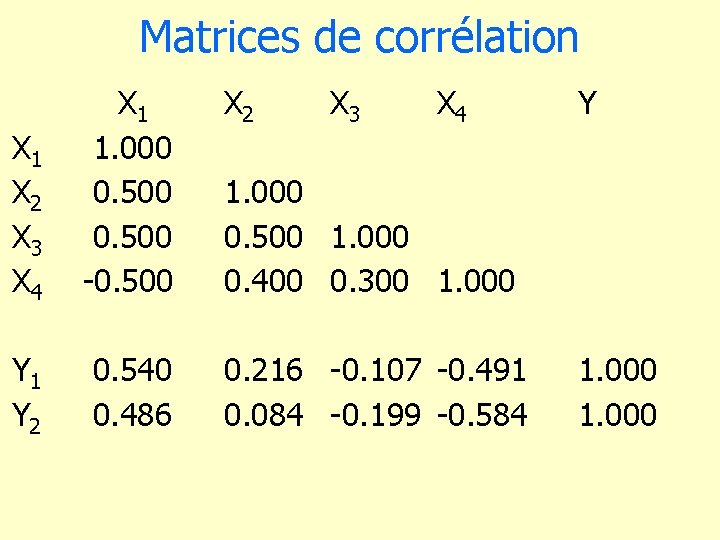
Matrices de corrélation X 2 X 1 X 2 X 3 X 4 X 1 1. 000 0. 500 -0. 500 X 3 X 4 Y 1 Y 2 0. 540 0. 486 0. 216 -0. 107 -0. 491 0. 084 -0. 199 -0. 584 Y 1. 000 0. 500 1. 000 0. 400 0. 300 1. 000