Link layer Error Detection and Correction PSU 1

Link layer Error Detection and Correction PSU 1

Link Layer l l PSU Link Layer protocol : defines the format of the packets exchanged DLC protocol data unit (D-PDU) Ø Ø Ø Packet Frame Block Cell (ATM) etc. 2

Services provided by the Link Layer Function l Synchronization (Framing) : Identify the beginning and end of data blocks Ø Ø l PSU Defining beginning and/or ending bit patterns synchronous transmission Transmission of data character by character asynchronous transmission Addressing Modes (Link Access) : provide a way to identify a recipient or a group of recipients of a PDU 3

Cont. l Connection set up and termination (Reliable deliver) l l l PSU allow the sending station to inform the receiving station of its wish to send data set up Sending station inform the receiver to release allocated resources termination Error Control : defined as the capability of detecting and recovering from errors in the received data l l Error detection Error correction 4

Cont. l l l PSU Flow Control : defined a set of procedures implemented to stop the transmitter from overwhelming the receiver with data Link Control and Testing : invoked in order to supervise and test link condition as a part of logical circuit maintenance Multiplexing : support many different protocol to be use at the same time 5

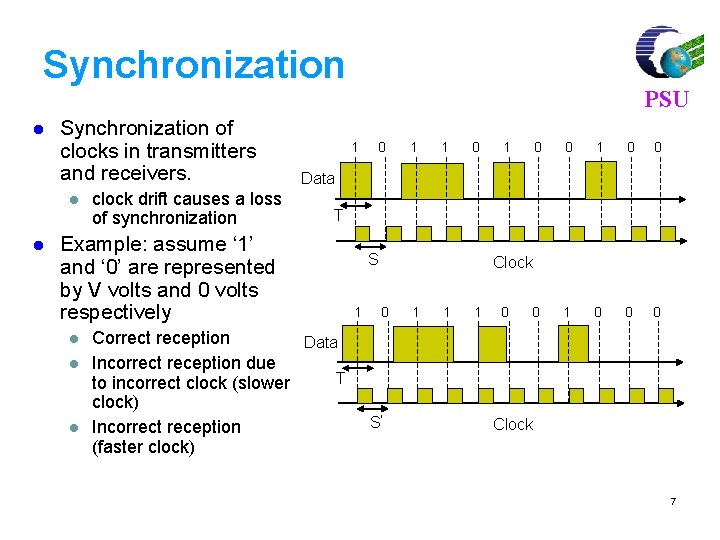
Synchronization l l l PSU Concerned with timing issues How does the receiver know when the bit period begins and ends? Small timing difference become more significant over time if no synchronization takes place between sender and receiver 6

Synchronization l Synchronization of clocks in transmitters and receivers. l l clock drift causes a loss of synchronization 1 l l 0 1 1 0 0 0 Data T Example: assume ‘ 1’ and ‘ 0’ are represented by V volts and 0 volts respectively l PSU Correct reception Data Incorrect reception due T to incorrect clock (slower clock) Incorrect reception (faster clock) S 1 Clock 0 S’ 1 1 1 0 Clock 7

Synchronization (cont’d) l PSU How to avoid a loss of synchronization? l Asynchronous transmission l Synchronous transmission 8

Synchronous Transmission l l l Large blocks of bits transmitted without start/stop codes Synchronized by clock signal or clocking data Data framed by preamble and postamble bit patterns l l l PSU More efficient than asynchronous Overhead typically below 5% Used at higher speeds than asynchronous 9

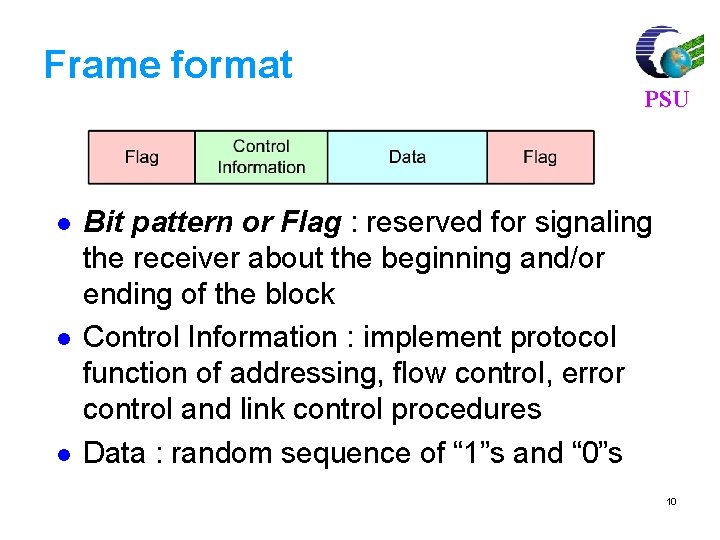
Frame format l l l PSU Bit pattern or Flag : reserved for signaling the receiver about the beginning and/or ending of the block Control Information : implement protocol function of addressing, flow control, error control and link control procedures Data : random sequence of “ 1”s and “ 0”s 10

Bit Stuffing l l PSU Prevent the occurrence of the flag pattern in PDU field Example l l Flag = 1010 Data = 1010101 xxx Bit stuffing : insert “ 1” whenever the following 7 -bit pattern occurs in data field l 10101011 xxx Bit stuffing 11

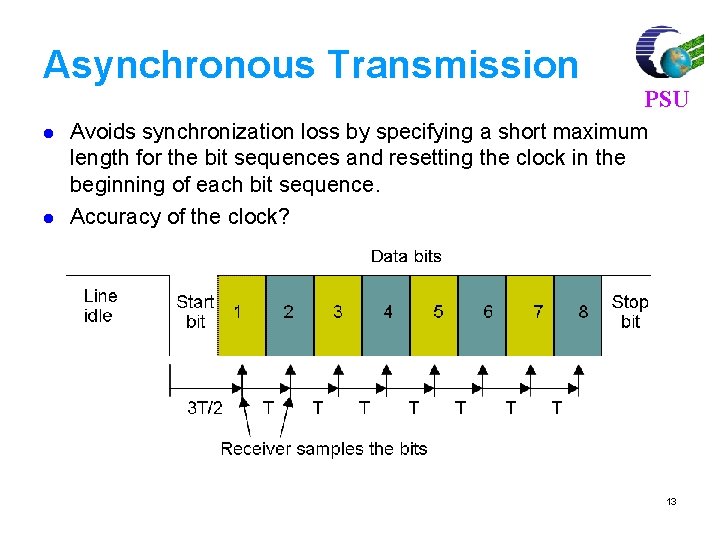
Asynchronous Transmission l l l Data transmitted 1 character at a time Character format is 1 start & 1+ stop bit, plus data of 5 -8 bits Character may include parity bit l l PSU Timing needed only within each character Resynchronization each start bit Uses simple, cheap technology Wastes 20 -30% of bandwidth 12

Asynchronous Transmission l l PSU Avoids synchronization loss by specifying a short maximum length for the bit sequences and resetting the clock in the beginning of each bit sequence. Accuracy of the clock? 13

Example l PSU Consider asynchronous transmission in the form of 7 -bit characters with one start bit and 1. 5 stop bits. For a 10 kbps link, let the sampling instants at the receiver be in the middle of each bit. What is the maximum tolerance of the alignment between the transmitter and receiver clocks for correct reception of character on this line? 14

Solution l l l PSU The bit duration = 1/10 kbps = 100 µsec Assume that the transmitter and receiver clocks are aligned at the beginning of the start bit. = discrepancy between the transmitter and receiver clocks 15

Cont. l l PSU Discrepancy of the two clocks at the middle of the start bit = /2 sec Discrepancy of the two clocks at the middle of the 1 st character = + /2 sec Discrepancy of the two clocks at the middle of the 7 th character = 7 + /2 sec = 15 /2 As long as this total discrepancy is less than half bit time (50 µsec), there is no error 16

Cont. l PSU Therefore the maximum value of tolerance max satisfy the following equation l l 15 max/2 = 50 µsec max = 20/3 µsec = 6. 67 µsec 17

Cont. l l l PSU General result Let R = bit rate (bps) n = number of bits in character + start pulse 18

Error Detection & Correction PSU 19

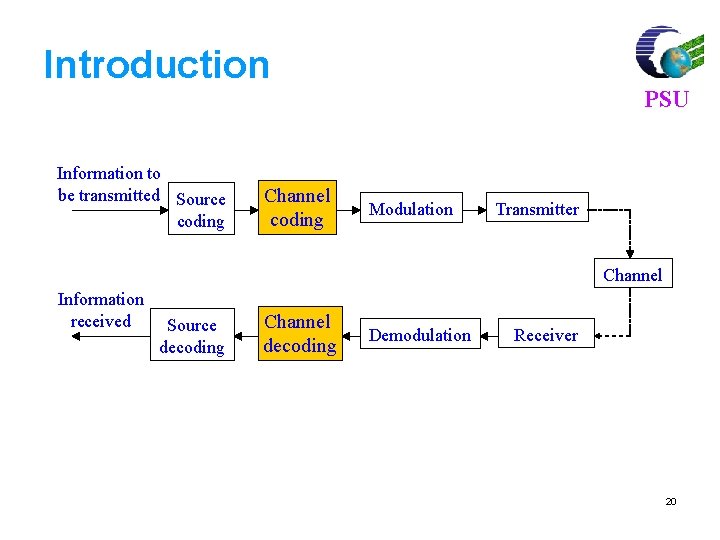
Introduction Information to be transmitted Source coding Channel coding PSU Modulation Transmitter Channel Information received Source decoding Channel decoding Demodulation Receiver 20

Noisy Communications l l PSU Noise in a communications channel can cause errors in the transmission of binary digits. Transmit: 1 1 0 0 1 0 1 1 1 0 0 1 0 … Receive: 1 1 0 1 0 0 0 0 1 0 … For some types of information, errors can be detected and corrected but not in others. Example: Transmit: Receive: Come to my house at 17: 25 … Come tc my houzx at 14: 25 … 21

PSU l In binary error correcting codes, only certain binary sequences (called code words) are transmitted. l This is similar to having a dictionary of allowable words. l After transmission over a noisy channel, we can check to see if the received binary sequence is in the dictionary of code words and if not, choose the codeword most similar to what was received. 22

Types of Errors PSU l Single-Bit Error : In a single-bit error, only one bit in the data unit has changed. l Burst Error : A burst error means that 2 or more bits in the data unit have changed. 23

Single-bit error PSU 24

Burst error of length 5 PSU 25

Error Control l l Digital transmission systems introduce errors Applications require certain reliability level l l PSU Data applications require error-free transfer Voice & video applications tolerate some errors Error control used when transmission system does not meet application requirement Error control ensures a data stream is transmitted to a certain level of accuracy despite errors Two basic approaches for Error control: l Error detection & retransmission (ARQ) l Forward error correction (FEC) 26

Two basic approaches for Error control l l PSU ARQ (Automatic Retransmission Request) – Involves the detection of errors and then an automatic retransmission request FEC (Forward Error Correction) – Involves the detection of errors followed by further processing of the received information that attempts to correct the errors 27

PSU l Error detection is the first step to both ARQ and FEC – The differenc is that ARQ “wastes” bandwidth with retransmissions whereas FEC requires extra redundancy and processing 28

Error Detection PSU Error detection uses the concept of redundancy, which means adding extra bits for detecting errors at the destination 29

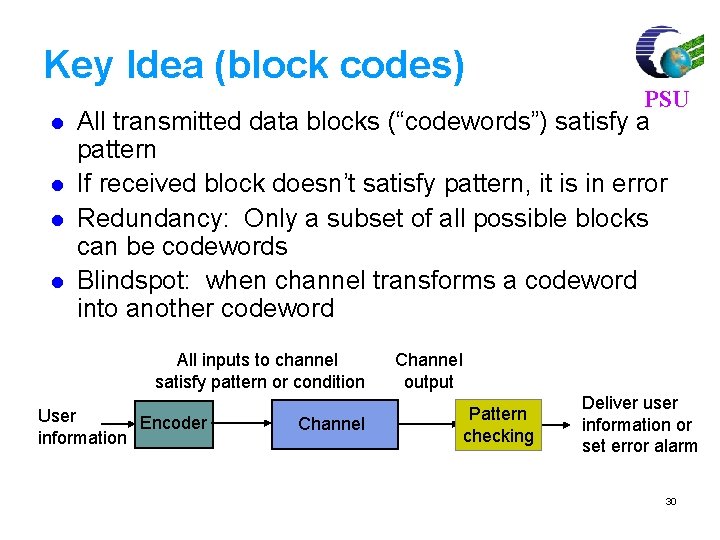
Key Idea (block codes) l l PSU All transmitted data blocks (“codewords”) satisfy a pattern If received block doesn’t satisfy pattern, it is in error Redundancy: Only a subset of all possible blocks can be codewords Blindspot: when channel transforms a codeword into another codeword All inputs to channel satisfy pattern or condition User Encoder information Channel output Pattern checking Deliver user information or set error alarm 30

PSU 31

Block Codes Message Source k binary digits 0101. . . 1 PSU Block Encoder n binary digits, n > k 0101. . . 1100. . . 1 Rate = k/n l l l Data = k bits Block Codes = n bits Redundant = n - k 32

Detection Method l l PSU Parity Check Internet Checksum Polynomial Codes Linear Codes 33

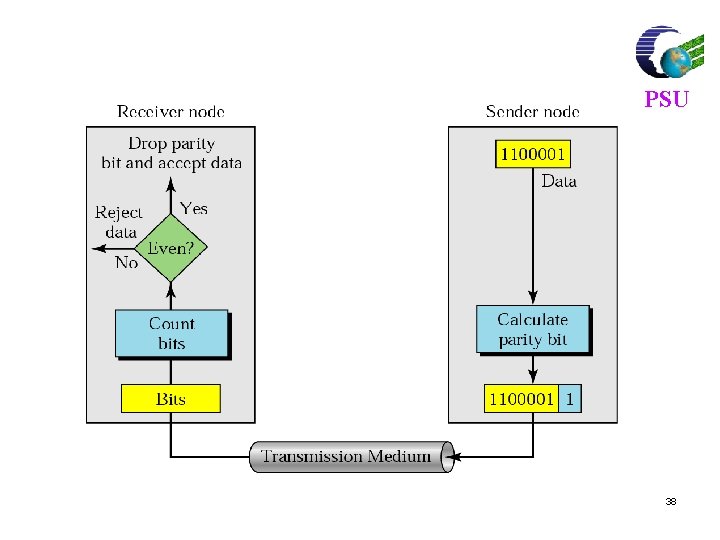
Single Parity Check PSU l l l Takes k information bits and appends a single check bit to form a codeword Ensures the total number of 1 s in the codeword is even (or odd) Used in ASCII where characters are represented by seven bits and the eighth bit is the parity bit 34

Error detection l Append an overall parity check to k information bits Info Bits: Check Bit: Codeword: l l PSU b 1, b 2, b 3, …, bk bk+1= b 1+ b 2+ b 3+ …+ bk modulo 2 (b 1, b 2, b 3, …, bk, , bk+!) All codewords always contain an even number of 1 s Receiver checks to see if # of 1 s is even l l All error patterns that change an odd # of bits are detectable All even-numbered patterns are undetectable 35

Example of Single Parity Code PSU Information (7 bits): (0, 1, 1, 0, 0) Parity Bit: b 8 = 0 + 1 +1 + 0 = 1 Codeword (8 bits): (0, 1, 1, 0, 0, 1) l If single error in bit 3 : (0, 1, 1, 0, 0, 1) l l l # of 1’s =5, odd Error detected If errors in bits 3 and 5: (0, 1, 1, 1, 0, 0, 0, 1) l l # of 1’s =4, even Error not detected 36

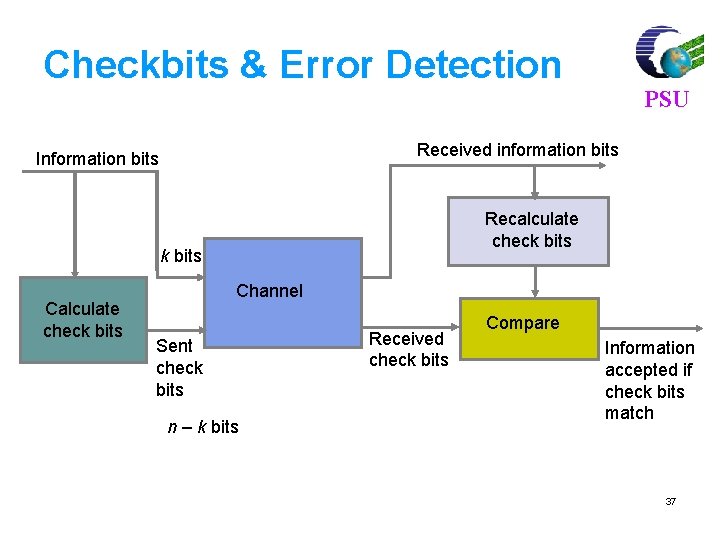
Checkbits & Error Detection Received information bits Information bits Recalculate check bits Calculate check bits PSU Channel Sent check bits n – k bits Received check bits Compare Information accepted if check bits match 37

PSU 38

How good is the single parity check code? l l Redundancy: Single parity check code adds 1 redundant bit per k information bits: overhead = 1/(k + 1) Coverage: all error patterns with odd # of errors can be detected l l PSU An error pattern is a binary (k + 1)-tuple with 1 s where errors occur and 0’s elsewhere Of 2 k+1 binary (k + 1)-tuples, ½ are odd, so 50% of error patterns can be detected Is it possible to detect more errors if we add more check bits? Yes, with the right codes 39

Effectiveness of Error-Detection Codes PSU Effectiveness of an error-detection code is measured by the probability that the system fails to detect an error l Depends on the particular properties of the given communication channel l Model of error channels: l l Random error vector model Random bit error model Burst error 40

Random error vector model l l PSU Codeword = n bits Define error vector e = (e 1, e 2, …, en) where ei = 1 if error occurs in the ith transmitted and ei = 0 otherwise l l Possible Codeword = 2 n All 2 n possible error vector are equally likely ot occur. probability of e does not depend on the number of errors it contains. p(1, 0, 0, 0, 1) = p(1, 0, 1, 1, 0, 0, 0, 1) = p(1, 1, 1) 41

Random bit error model l PSU Let p : probability of an error in single-bit transmission Probability of an error vector that has j errors is pj(1 -p)n-j since each of the j errors occurs with probability p and each of the n - j correct transmission occurs with probability 1 – p Then codeword is probability: p[e] = (1 -p)n-n(e)p(w(e) = (1 -p)n( 42

PSU l l Using the model that any error pattern is equally likely to happen is random error vector model Bit error occur independently of each other so random bit error model implies that an error pattern with a given number of bit errors is more likely than an error pattern with a larger number of bit errors 43

What if bit errors are random? l l PSU Many transmission channels introduce bit errors at random, independently of each other, and with probability p Some error patterns are more probable than others: p and 1–p 2 6 8 P[11000000] = p (1 – p) = (1 – p) 1–p P[10000000] = p(1 – p)7 = (1 – p)8 l l l In any worthwhile channel p < 0. 5, and so (p/(1 – p) < 1 It follows that patterns with 1 error are more likely than patterns with 2 errors and so forth What is the probability that an undetectable error pattern occurs? 44

Single parity check code with random bit errors l PSU Undetectable error pattern if even # of bit errors: P[error detection failure] = P[undetectable error pattern] = P[error patterns with even number of 1 s] = l n 2 p (1 – p)n-2 + 2 n 4 p 4(1 – p)n-4 + … Example: Evaluate above for n = 32, p = 10 -3 P[undetectable error] = 32 32 (10 -3)2 (1 – 10 -3)30 + (10 -3)4 (1 – 10 -3)28 2 4 ≈ 496 (10 -6) + 35960 (10 -12) ≈ 4. 96 (10 -4) l For this example, roughly 1 in 2000 error patterns is undetectable 45

What is a good code? l l Many channels have preference for error patterns that have fewer # of errors These error patterns map transmitted codeword to nearby n-tuple If codewords close to each other then detection failures will occur Good codes should maximize separation between codewords PSU o o x x x o o o Poor distance properties x = codewords o = noncodewords o x x o o o x x Good distance properties 46

Two-Dimensional Parity Check l l l More parity bits to improve coverage Arrange information as columns Add single parity bit to each column Add a final “parity” column Used in early error control systems PSU 1 0 0 0 1 Last column consists 1 0 0 of check bits for each 1 1 0 row 1 0 0 1 1 1 Bottom row consists of check bit for each column 47

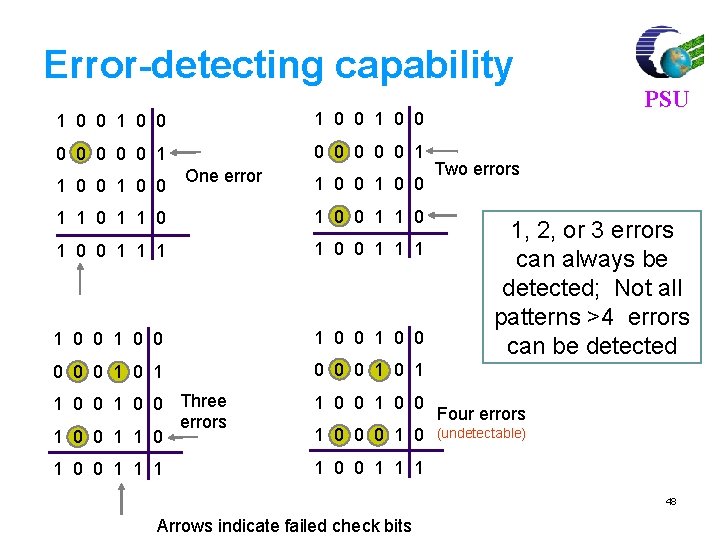
Error-detecting capability 1 0 0 0 0 0 0 0 1 1 0 0 One error 1 0 0 1 1 0 0 1 1 1 1 0 0 1 0 0 0 1 1 0 0 Three errors 1 0 0 1 0 0 1 1 1 1 0 0 0 1 0 PSU Two errors 1, 2, or 3 errors can always be detected; Not all patterns >4 errors can be detected Four errors (undetectable) 48 Arrows indicate failed check bits

Other Error Detection Codes l l l PSU Many applications require very low error rate Need codes that detect the vast majority of errors Single parity check codes do not detect enough errors Two-dimensional codes require too many check bits The following error detecting codes used in practice: l Internet Check Sums l CRC Polynomial Codes 49

Internet Checksum l l l PSU Several Internet protocols (e. g. IP, TCP, UDP) use check bits to detect errors in the IP header (or in the header and data for TCP/UDP) A checksum is calculated for header contents and included in a special field. Checksum recalculated at every router, so algorithm selected for ease of implementation in software Let header consist of L, 16 -bit words, b 0, b 1, b 2, . . . , b. L-1 The algorithm appends a 16 -bit checksum b. L 50

Checksum Calculation PSU The checksum b. L is calculated as follows: l Treating each 16 -bit word as an integer, find x = b 0 + b 1 + b 2+. . . + b. L-1 modulo 216 -1 l The checksum is then given by: b. L = - x modulo 216 -1 Thus, the headers must satisfy the following pattern: 0 = b 0 + b 1 + b 2+. . . + b. L-1 + b. L modulo 216 -1 l The checksum calculation is carried out in software using one’s complement arithmetic 51

Internet Checksum Example Use Modulo Arithmetic l Assume 4 -bit words l Use mod 24 -1 arithmetic b 0=1100 = 12 b 1=1010 = 10 b 0+b 1=12+10=7 mod 15 b 2 = -7 = 8 mod 15 l Therefore b 2=1000 PSU Use Binary Arithmetic l Note 16 =1 mod 15 l So: 10000 = 0001 mod 15 l leading bit wraps around b 0 + b 1 = 1100+1010 =10110 =10000+0110 =0001+0110 =0111 =7 Take 1 s complement b 2 = -0111 =1000 52

Example PSU Suppose the following block of 16 bits is to be sent using a checksum of 8 bits. 10101001 00111001 The numbers are added using one’s complement 10101001 00111001 ------Sum 11100010 Checksum 00011101 l The pattern sent is 10101001 00111001 00011101 53

PSU Now suppose the receiver receives the pattern sent in previous example and there is no error. 10101001 00111001 00011101 l When the receiver adds the three sections, it will get all 1 s, which, after complementing, is all 0 s and shows that there is no error. 10101001 00111001 00011101 Sum 1111 Complement 0000 means that the pattern is OK. 54

PSU Now suppose there is a burst error of length 5 that affects 4 bits. 101011111001 00011101 When the receiver adds the three sections, it gets 101011111001 00011101 Partial Sum 1 11000101 Carry 1 Sum 11000110 Complement 00111001 the pattern is corrupted 55

Polynomial Codes l l l PSU Polynomials instead of vectors for codewords Polynomial arithmetic instead of check sums Implemented using shift-register circuits Also called cyclic redundancy check (CRC) codes Most data communications standards use polynomial codes for error detection Polynomial codes also basis for powerful error-correction methods 56

PSU 57

Binary Polynomial Arithmetic l Binary vectors map to polynomials PSU (ik-1 , ik-2 , …, i 2 , i 1 , i 0) ik-1 xk-1 + ik-2 xk-2 + … + i 2 x 2 + i 1 x + i 0 Addition: (x 7 + x 6 + 1) + (x 6 + x 5) = x 7 + x 6 + x 5 + 1 = x 7 +(1+1)x 6 + x 5 + 1 = x 7 +x 5 + 1 since 1+1=0 mod 2 Multiplication: (x + 1) (x 2 + x + 1) = x(x 2 + x + 1) + 1(x 2 + x + 1) = (x 3 + x 2 + x) + (x 2 + x + 1) = x 3 + 1 58

Binary Polynomial Division with Decimal Numbers 34 35 ) 1222 105 divisor 17 2 140 32 l PSU quotient dividend = quotient x divisor +remainder 1222 = 34 x 35 + 32 remainder Polynomial Division divisor x 3 + x 2 + x = q(x) quotient x 3 + x + 1 ) x 6 + x 5 x 6 + x 4 + x 3 Note: Degree of r(x) is less than degree of divisor dividend x 5 + x 4 + x 3 x 5 + x 3 + x 2 x 4 + x 2 + x x 59 = r(x) remainder

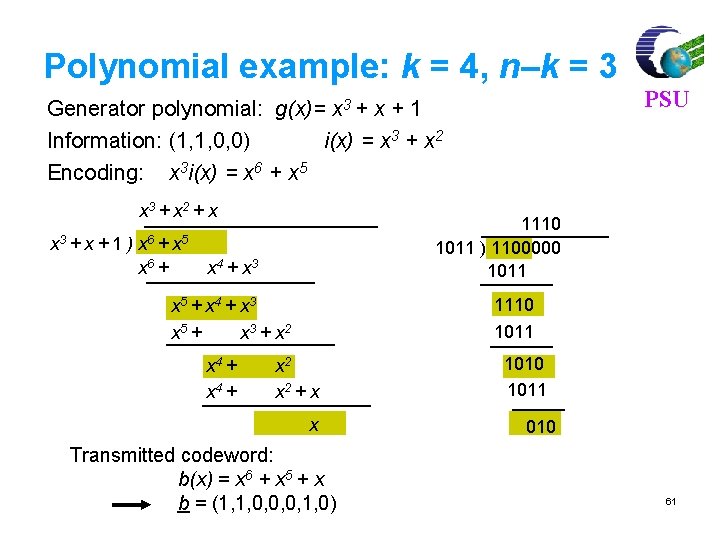
Polynomial Coding PSU l Code has binary generating polynomial of degree n–k l g(x) = xn-k + gn-k-1 xn-k-1 + … + g 2 x 2 + g 1 x + 1 k information bits define polynomial of degree k – 1 i(x) = ik-1 xk-1 + ik-2 xk-2 + … + i 2 x 2 + i 1 x + i 0 l Find remainder polynomial of at most degree n – k – 1 l q(x) xn-ki(x) = q(x)g(x) + r(x) g(x) ) xn-k i(x) r(x) Define the codeword polynomial of degree n – 1 b(x) = xn-ki(x) + r(x) n bits k bits n-k bits 60

Polynomial example: k = 4, n–k = 3 Generator polynomial: g(x)= x 3 + x + 1 Information: (1, 1, 0, 0) i(x) = x 3 + x 2 Encoding: x 3 i(x) = x 6 + x 5 x 3 + x 2 + x x 3 + x + 1 ) x 6 + x 5 x 6 + 1110 1011 ) 1100000 1011 x 4 + x 3 1110 1011 x 5 + x 4 + x 3 x 5 + x 3 + x 2 x 4 + PSU x 2 + x x Transmitted codeword: b(x) = x 6 + x 5 + x b = (1, 1, 0, 0, 0, 1, 0) 1010 1011 010 61

The Pattern in Polynomial Coding l PSU All codewords satisfy the following pattern: b(x) = xn-ki(x) + r(x) = q(x)g(x) l l l All codewords are a multiple of g(x)! Receiver should divide received n-tuple by g(x) and check if remainder is zero If remainder is nonzero, then received n-tuple is not a codeword 62

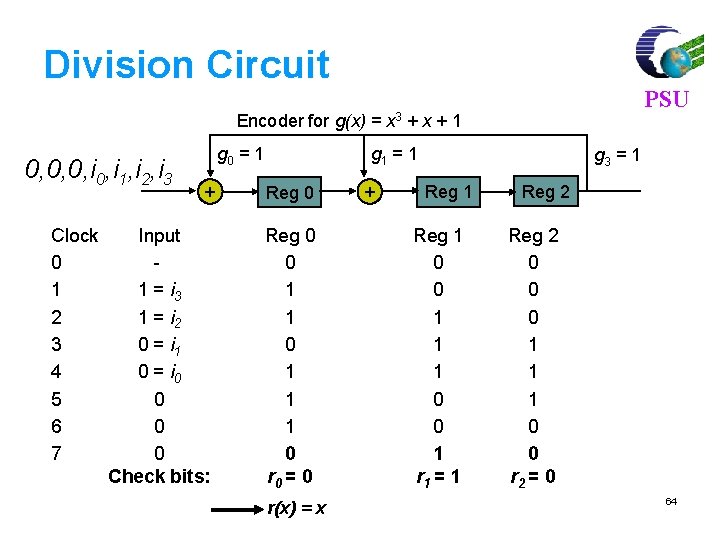
Shift-Register Implementation 1. 2. 3. 4. PSU Accept information bits ik-1, ik-2, …, i 2, i 1, i 0 Append n – k zeros to information bits Feed sequence to shift-register circuit that performs polynomial division After n shifts, the shift register contains the remainder 63

Division Circuit PSU Encoder for g(x) = x 3 + x + 1 0, 0, 0, i 1, i 2, i 3 Clock 0 1 2 3 4 5 6 7 g 0 = 1 + Input 1 = i 3 1 = i 2 0 = i 1 0 = i 0 0 Check bits: g 1 = 1 Reg 0 0 1 1 1 0 r 0 = 0 r(x) = x + g 3 = 1 Reg 1 0 0 1 1 1 0 0 1 r 1 = 1 Reg 2 0 0 0 1 1 1 0 0 r 2 = 0 64

Undetectable error patterns (Transmitter) b(x) (Receiver) + PSU R(x)=b(x)+e(x) (Channel) e(x) Error polynomial l l e(x) has 1 s in error locations & 0 s elsewhere Receiver divides the received polynomial R(x) by g(x) Blindspot: If e(x) is a multiple of g(x), that is, e(x) is a nonzero codeword, then R(x) = b(x) + e(x) = q(x)g(x) + q’(x)g(x) The set of undetectable error polynomials is the set of nonzero code polynomials Choose the generator polynomial so that selected error patterns can be detected. 65

Designing good polynomial codes l l Select generator polynomial so that likely error patterns are not multiples of g(x) Detecting Single Errors l l l PSU e(x) = xi for error in location i + 1 If g(x) has more than 1 term, it cannot divide xi Detecting Double Errors l l e(x) = xi + xj = xi(xj-i+1) where j>i If g(x) has more than 1 term, it cannot divide xi If g(x) is a primitive polynomial, it cannot divide xm+1 for all m<2 n-k-1 (Need to keep codeword length less than 2 n-k-1) Primitive polynomials can be found by consulting coding theory books 66

Designing good polynomial codes l PSU Detecting Odd Numbers of Errors l l Suppose all codeword polynomials have an even # of 1 s, then all odd numbers of errors can be detected As well, b(x) evaluated at x = 1 is zero because b(x) has an even number of 1 s This implies x + 1 must be a factor of all b(x) Pick g(x) = (x + 1) p(x) where p(x) is primitive 67

Designing good polynomial codes l PSU Errors bursts of length b l l l e(x) = xid(x) where deg(d(x)) = L - 1 g(x) has degree n – k g(x) cannot divide d(x) if deg(g(x)) > deg(d(x)) L 0000 110 … 00011011 00… 0 Error pattern d(x) 68

Standard Generator Polynomials CRC = cyclic redundancy check l CRC-8: = x 8 + x 2 + x + 1 l Bisync CCITT-16: = x 16 + x 12 + x 5 + 1 l ATM CRC-16: = x 16 + x 15 + x 2 + 1 = (x + 1)(x 15 + x + 1) l PSU CCITT-32: HDLC, XMODEM, V. 41 IEEE 802, Do. D, V. 42 = x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 + x 8 + x 7 + x 5 + x 4 + x 2 + x + 1 69

Advantages of CRC’s l l PSU CRCs detect a larger proportion of the possible errors CRCs are practical and efficient to implement CRCs can be efficiently applied to larger blocks of data CRCs use more parity bits (usually 8, 12, 16, or 32), but often use fewer parity bits per bit of data 70

Linear Block Codes PSU l l l Information is divided into blocks of length k r parity bits or check bits are added to each block (total length n = k + r), . Code rate R = k/n Decoder looks for codeword closest to received vector (code vector + error vector) Tradeoffs between l l l Efficiency Reliability Encoding/Decoding complexity 71

Linear Block Codes l l l PSU The uncoded k data bits be represented by the m vector: m=(m 1, m 2, …, mk) The corresponding codeword be represented by the n-bit c vector: c=(c 1, c 2, …ck, ck+1, …, cn-1, cn) Each parity bit consists of weighted modulo 2 sum of the data bits represented by symbol. 72

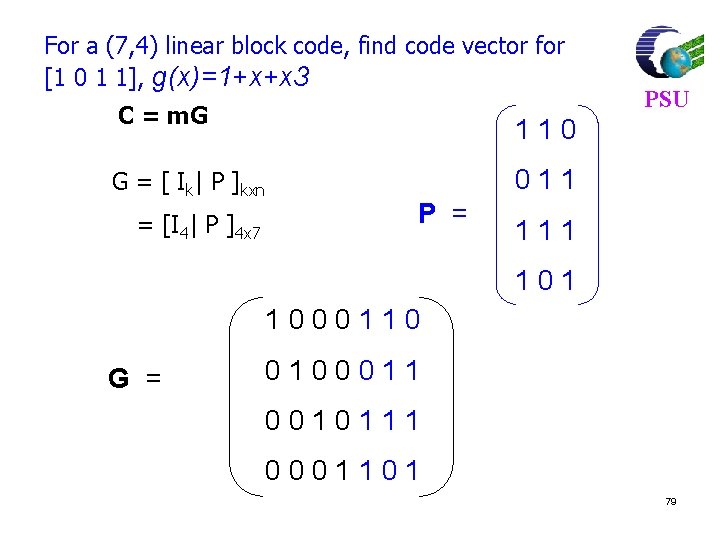
Linear Block Codes § Linear Block Code PSU The block length C of the Linear Block Code is C=m. G where m is the information codeword block length, G is the generator matrix. G = [Ik | P]k × n, where pi = Remainder of [xn-k+i-1/g(x)] for i=1, 2, . . , k, and I is unit matrix. § The parity check matrix H = [PT | In-k ], where PT is the transpose of the matrix p. 73

Block Codes: Example PSU Example : Find linear block code encoder G if code generator polynomial g(x)=1+x+x 3 for a (7, 4) code. We have n = Total number of bits = 7, k = Number of information bits = 4, r = Number of parity bits = n - k = 3. where 74

Block Codes: Example (Cont’d) PSU 75

Block Codes: Linear Block Codes Message vector Generator matrix Code Vector Parity check matrix m G C C HT PSU Null vector 0 Operations of the generator matrix and the parity check matrix The parity check matrix H is used to detect errors in the received code by using the fact that c * HT = 0 ( null vector) Let x = c e be the received message where c is the correct code and e is the error Compute S = x * HT =( c e ) * HT =c HT e HT = e H T If S is 0 then message is correct else there are errors in it, from common known error patterns the correct message can be decoded. 76

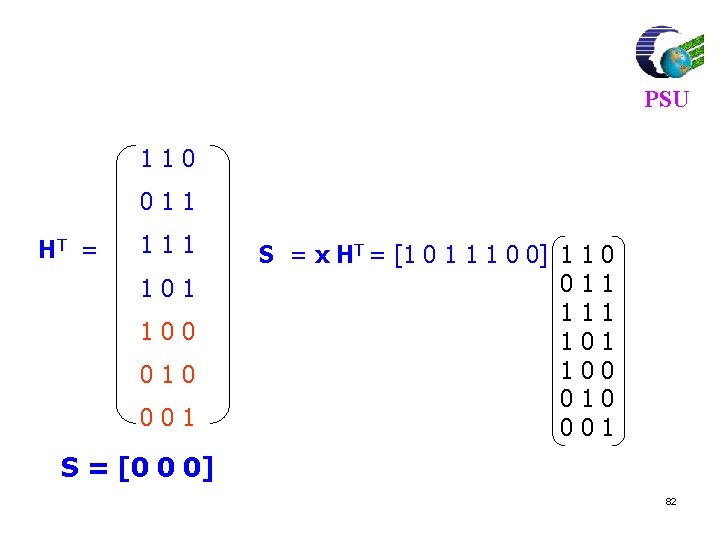
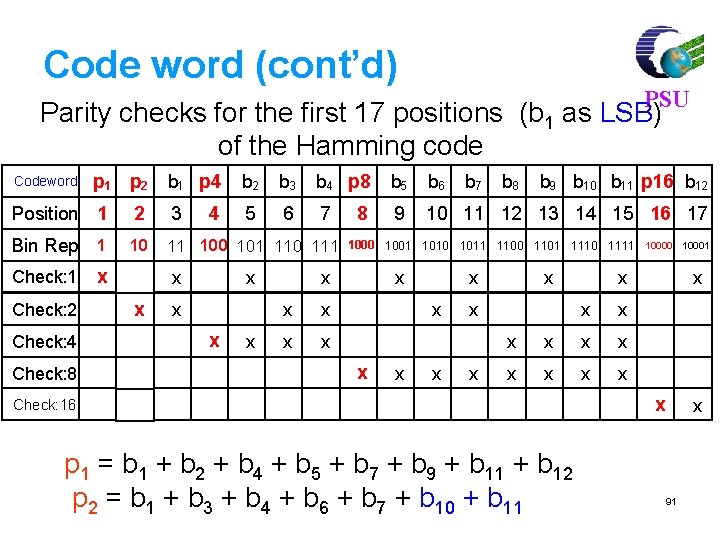
Linear Block Codes PSU Consider a (7, 4) linear block code, given by G as Then, For m = [1 0 1 1] and c = m. G = [1 0 1 1 0 0 1]. If there is no error, the received vector x=c, and s=c. HT=[0, 0, 0] 77

Linear Block Codes PSU Let c suffer an error such that the received vector x=c e =[ 1 0 1 1 0 0 1 ] [ 0 0 1 0 0 ] =[ 1 0 0 1 ] Then, s=x. HT = =(e. HT) 78

For a (7, 4) linear block code, find code vector for [1 0 1 1], g(x)=1+x+x 3 C = m. G 110 G = [ Ik| P ]kxn = [I 4| P ]4 x 7 PSU 011 P = 111 1000110 G = 0100011 0010111 0001101 79

For m = [ 1 0 1 1], code vector is PSU C=m. G C= [1 0 1 1] 1 0 0 0 1 1 0 0100011 0010111 0001101 = [ 1 0 1 1 1 0 0] 80

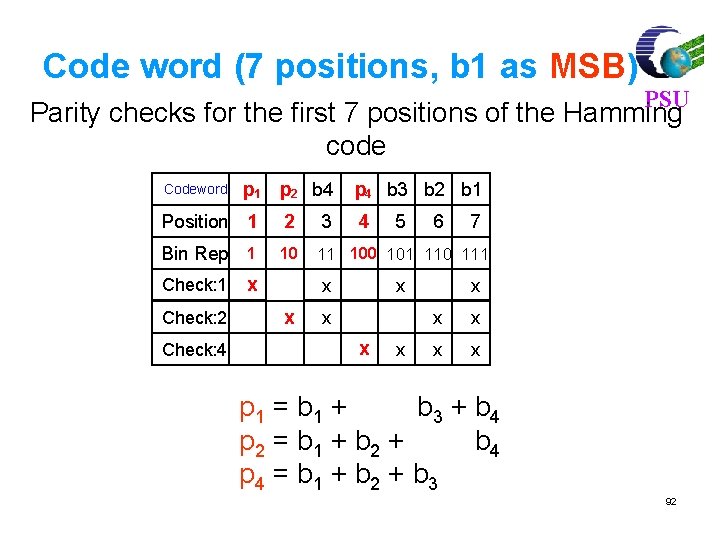
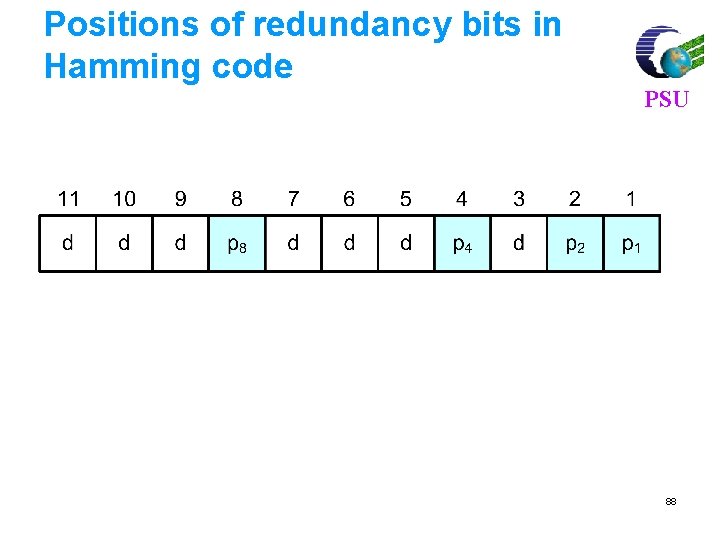
For (7, 4) code, find syndrome for x = [1011000] x=c e PSU =[ 1 0 1 1 0 0 0 ] [ 0 0 0 0 ] =[ 1 0 1 1 0 0 0 ] Syndrome S = x HT H = [PT|In-k] = 101110010 0111001 81

PSU 110 011 HT = 111 100 010 001 S = x HT = [1 0 1 1 1 0 0] 1 0 1 1 1 0 0 1 1 1 0 0 1 S = [0 0 0] 82

Hamming Codes l l Designed to correct single bit errors Family of (n, k) block error-correcting codes with parameters: l l l PSU Block length: n = 2 m – 1 Number of data bits: k = 2 m – 1 Number of check bits: n – k = m Minimum distance: dmin = 3 Single-error-correcting (SEC) code l SEC double-error-detecting (SEC-DED) code 83

Hamming Codes (cont’d) l PSU For each m > 2, there is a Hamming code of length n = 2 m – 1 with n – k = m parity check bits Redundancy m 3 4 5 6 n = 2 m– 1 k = n–m 7 4 15 11 31 26 63 57 m/n 3/7 4/15 5/31 6/63 84

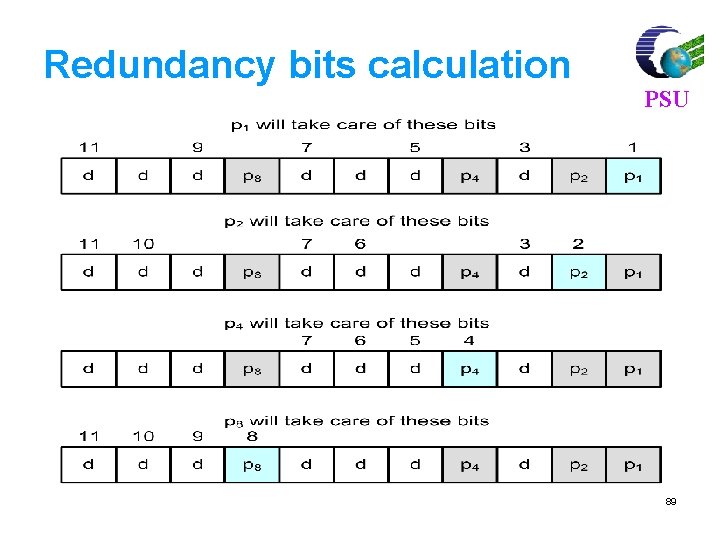
Hamming Codes (cont’d) l PSU Create the code word as follows: l l Mark all bit positions that are powers of two as parity bits). positions 1, 2, 4, 8, 16, 32, 64, etc(. All other bit positions are for the data to be encoded. )positions 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, etc) 85

Code word (cont’d) l PSU Each parity bit calculates the parity for some of the bits in the code word. The position of the parity bit determines the sequence of bits that it alternately checks and skips. Position 1 : check 1 bit, skip 1 bit, etc(. . . , 1, 3, 5, 7, 9, 11, 13, 15). Position 2 : check 2 bits, skip 2 bits, etc(. . . , 2, 3, 6, 7, 10, 11, 14, 15). Position 4 : check 4 bits, skip 4 bits, etc. (. . . , 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23) 86

Code word (cont’d) PSU Position 8 : check 8 bits, skip 8 bits, etc 8 -15, ). 24 -31, 40 -47, (. . . Position 16 : check 16 bits, skip 16 bits, etc 16 -31, ). 48 -63, 80 -95, (. . . Position 32 : check 32 bits, skip 32 bits, etc 32 -63, ). 96 -127, 160 -191, (. . . etc. l Set a parity bit to 1 if the total number of ones in the positions it checks is odd. Set a parity bit to 0 if the total number of ones in the positions it checks is even 87

Positions of redundancy bits in Hamming code PSU 88

Redundancy bits calculation PSU 89

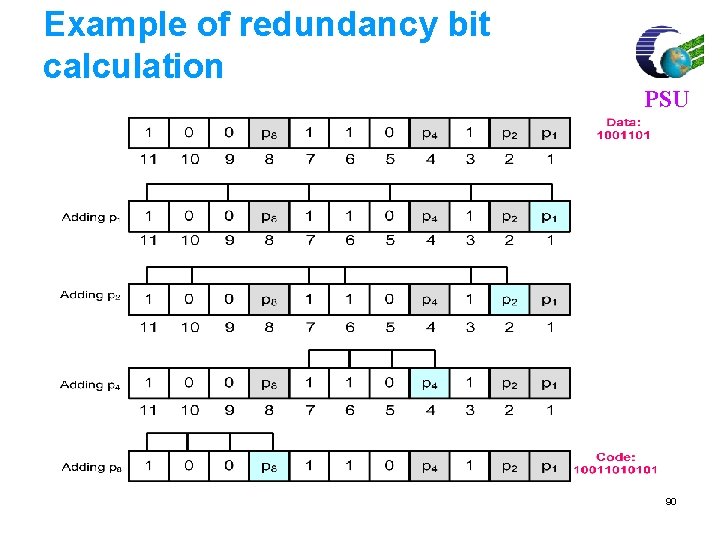
Example of redundancy bit calculation PSU 90

Code word (cont’d) PSU Parity checks for the first 17 positions (b 1 as LSB) of the Hamming code p 1 p 2 b 1 p 4 b 2 b 3 b 4 p 8 b 5 b 6 Position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 Bin Rep 1 10 11 100 101 110 111 Codeword Check: 1 Check: 2 Check: 4 Check: 8 x x x x x b 8 b 9 b 10 b 11 p 16 b 12 1000 1001 1010 1011 1100 1101 1110 1111 10000 10001 x x b 7 x x x x x Check: 16 p 1 = b 1 + b 2 + b 4 + b 5 + b 7 + b 9 + b 11 + b 12 p 2 = b 1 + b 3 + b 4 + b 6 + b 7 + b 10 + b 11 x x x 91

Code word (7 positions, b 1 as MSB) PSU Parity checks for the first 7 positions of the Hamming code p 2 b 4 p 4 b 3 b 2 b 1 Position 1 2 3 4 Bin Rep 1 10 11 100 101 110 111 Codeword Check: 1 Check: 2 Check: 4 p 1 x x x 5 6 x x 7 x x x p 1 = b 1 + b 3 + b 4 p 2 = b 1 + b 2 + b 4 p 4 = b 1 + b 2 + b 3 92

m = 3 Hamming Code l l Information bits are b 1, b 2, b 3, b 4 Equations for parity checks b 5, b 6, b 7 p 1 = b 5 = b 1 + b 3 + b 4 p 2 = b 6 = b 1 + b 2 p 4 = b 7 = l l PSU + b 4 + b 2 + b 3 + b 4 There are 24 = 16 codewords (0, 0, 0, 0) is a codeword 93

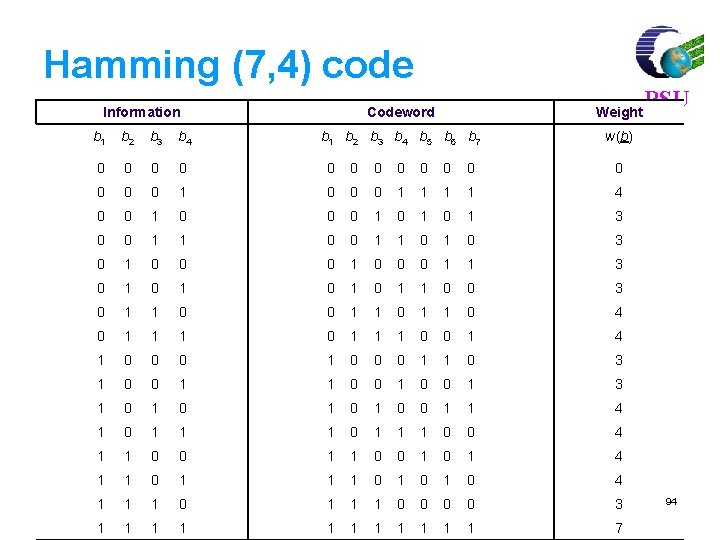
Hamming (7, 4) code Information Codeword Weight b 1 b 2 b 3 b 4 b 5 b 6 b 7 w(b) b 1 b 2 b 3 b 4 0 0 0 0 1 0 0 0 1 1 4 0 0 1 0 1 0 1 3 0 0 1 1 0 1 0 3 0 1 0 0 0 1 1 3 0 1 0 1 1 0 0 3 0 1 1 0 4 0 1 1 1 0 0 1 4 1 0 0 0 1 1 0 3 1 0 0 1 3 1 0 1 0 0 1 1 4 1 0 1 1 1 0 0 4 1 1 0 0 1 0 1 4 1 1 0 1 0 1 0 4 1 1 1 0 0 0 0 3 1 1 1 7 PSU 94

Parity Check Equations l Rearrange parity check equations: 0 = b 5 + b 5 = b 1 + b 3 + b 4 + b 5 0 = b 6 + b 6 = b 1 + b 2 0 = b 7 + b 7 = l In matrix form: + b 4 + b 6 + b 2 + b 3 + b 4 + b 7 b 1 l b 2 0 PSU = 1011100 b 3 0 = 1101010 b 4 = H 0 = 0111001 b 5 b 6 b 7 bt = [Pt|I n-k] bt =0 l All codewords must satisfy these equations Note: each nonzero 3 -tuple appears once as a column in check matrix H 95

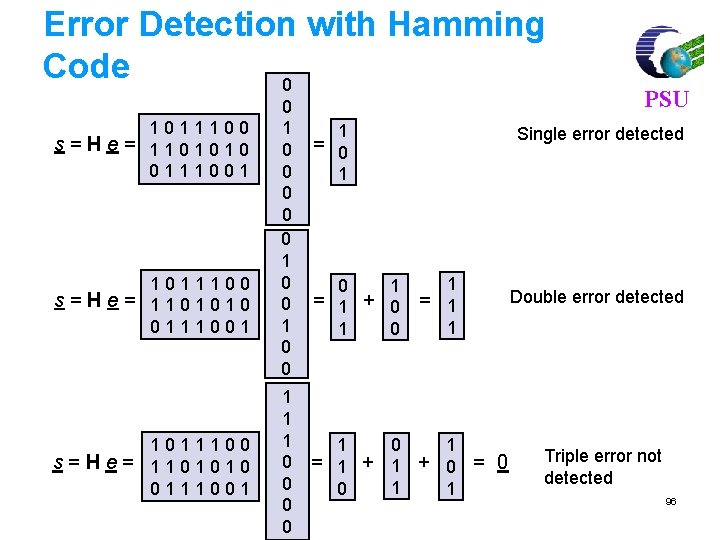
Error Detection with Hamming Code 0 1011100 s=He= 1101010 0111001 0 0 0 1 1 1 0 0 1 PSU Single error detected = 0 1 0 1 = 1 + 0 1 = 1 1 0 1 1 + 0 = 0 1 1 Double error detected Triple error not detected 96

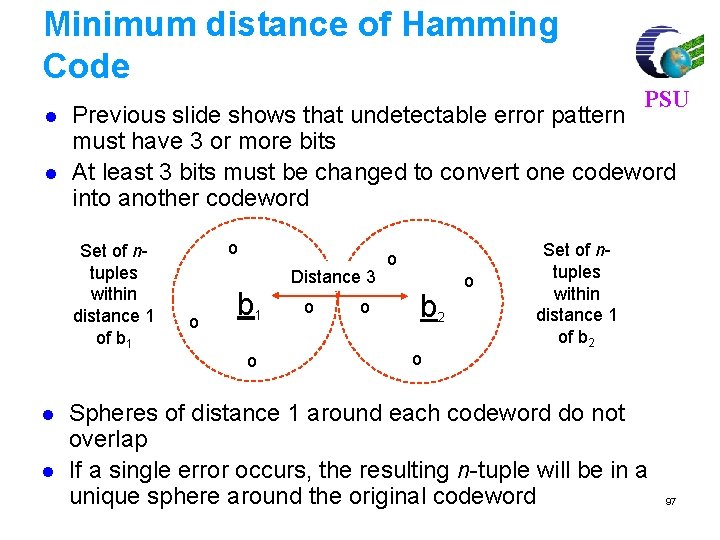
Minimum distance of Hamming Code l l Previous slide shows that undetectable error pattern must have 3 or more bits At least 3 bits must be changed to convert one codeword into another codeword Set of ntuples within distance 1 of b 1 l l PSU o o b 1 o Distance 3 o o o b 2 o o Set of ntuples within distance 1 of b 2 Spheres of distance 1 around each codeword do not overlap If a single error occurs, the resulting n-tuple will be in a unique sphere around the original codeword 97

General Hamming Codes l For m > 2, the Hamming code is obtained through the check matrix H: l l l PSU Each nonzero m-tuple appears once as a column of H The resulting code corrects all single errors For each value of m, there is a polynomial code with g(x) of degree m that is equivalent to a Hamming code and corrects all single errors l For m = 3, g(x) = x 3+x+1 98

Error-correction using Hamming Codes (Transmitter) b + PSU R (Receiver) e Error pattern l l l The receiver first calculates the syndrome: s = HR = H (b + e) = Hb + He = He If s = 0, then the receiver accepts R as the transmitted codeword If s is nonzero, then an error is detected l l l Hamming decoder assumes a single error has occurred Each single-bit error pattern has a unique syndrome The receiver matches the syndrome to a single-bit error pattern and corrects the appropriate bit 99

Performance of Hamming Error. Correcting Code l PSU Assume bit errors occur independent of each other and with probability p s = H R = H(b + e) = 0 + He 7 p s=0 No errors in transmission (1–p)7 Undetectable errors 7 p 3 s=0 1– 3 p Correctable errors 7 p(1– 3 p) 3 p Uncorrectable errors 21 p 2 100

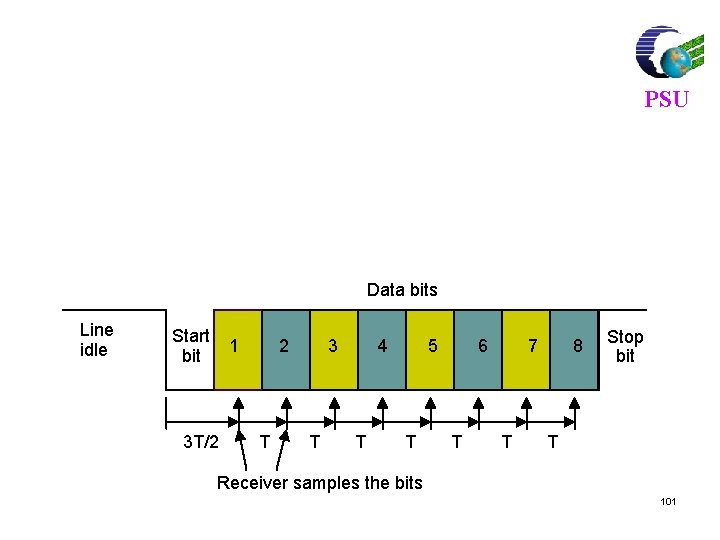
PSU Data bits Line idle Start bit 1 3 T/2 2 T 3 T 4 T 5 T 6 T 7 T 8 Stop bit T Receiver samples the bits 101

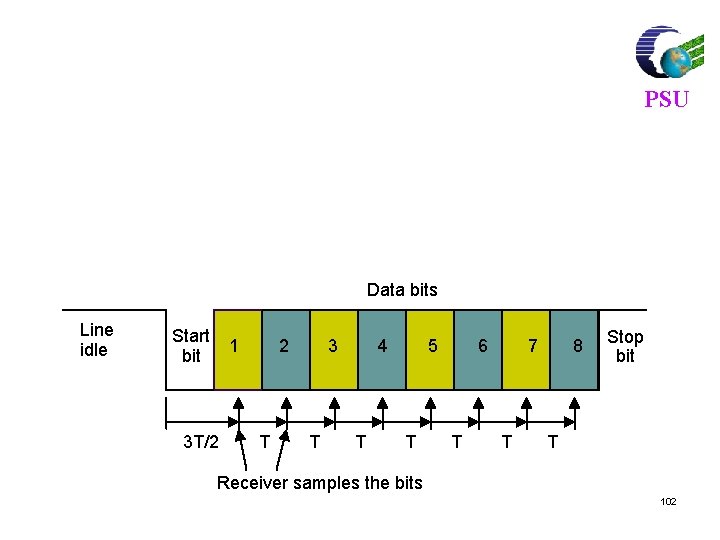
PSU Data bits Line idle Start bit 1 3 T/2 2 T 3 T 4 T 5 T 6 T 7 T 8 Stop bit T Receiver samples the bits 102