Coding and Error Control ReviewRecap Lecture 24 Overview

Coding and Error Control Review/Recap Lecture 24

Overview n n n n Parity Cyclic Redundancy Check (CRC) CRC for More than a Bit Error CRC Algorithms ECC Block ECC Convolutional Code 2

Parity Bit Q: - What is a parity bit? 3

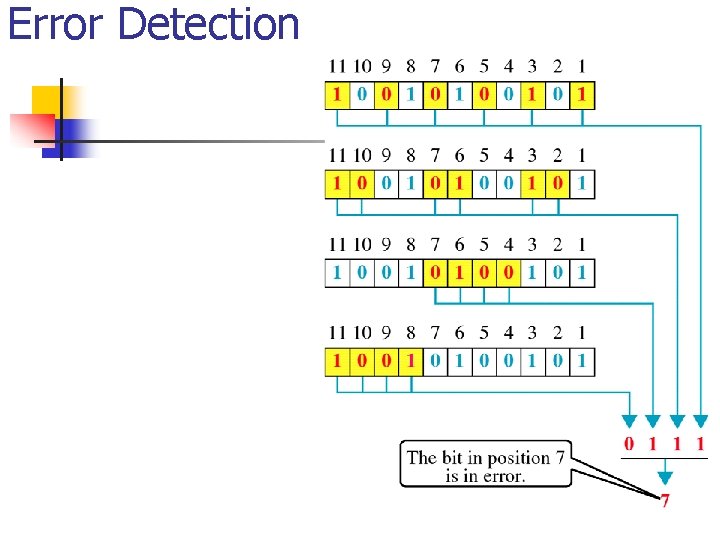
Error Detection n Detection methods

Error Detection(cont’d) n Parity Check n A parity bit is added to every data unit so that the total number of 1 s(including the parity bit) becomes even for even-parity check or odd for odd-parity check n Simple parity check

Parity Codes n n Known as a single error detecting code (SED). Only useful if probability of getting 2 errors is small since parity will become correct again Used in serial communications Low overhead but not very powerful Decoder can be implemented efficiently using a tree of XOR gates

7

Parity Codes n Example of a simple block code – Single Parity Check Code n n In this case, n = k+1, i. e. , the codeword is the dataword with one additional bit For ‘even’ parity the additional bit is, – For ‘odd’ parity the additional bit is 1 -q – That is, the additional bit ensures that there an ‘even’ or ‘odd’ number of ‘ 1’s in the codeword

Parity Codes – Example 1 n Even parity (i) d=(10110) so, c=(101101) (ii) d=(11011) so, c=(110110)

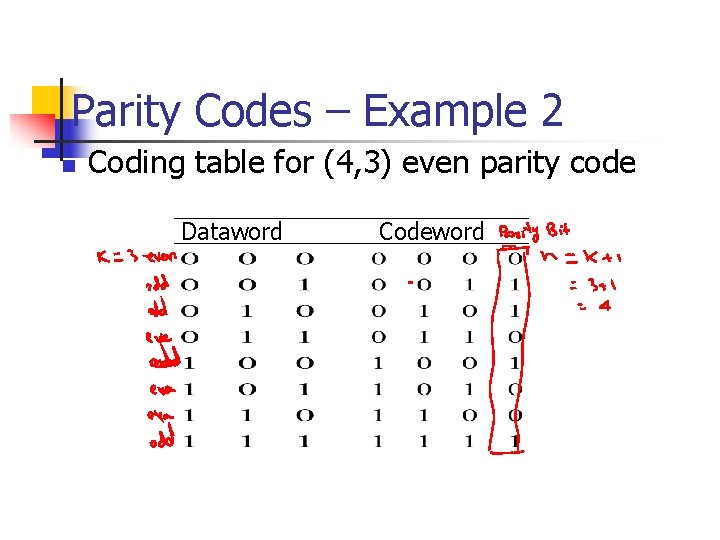
Parity Codes – Example 2 n Coding table for (4, 3) even parity code Dataword Codeword

Parity Codes n n n To decode n Calculate sum of received bits in block (mod 2) n If sum is 0 (1) for even (odd) parity then the dataword is the first k bits of the received codeword n Otherwise error Code can detect single errors But cannot correct error since the error could be in any bit For example, if the received dataword is (100000) the transmitted dataword could have been (000000) or (110000) with the error being in the first or second place respectively Note error could also lie in other positions including the parity bit

12

Parity Checks n Simple parity n n If performing even parity, add a parity bit such that an even number of 1 s are maintained If performing odd parity, add a parity bit such that an odd number of 1 s are maintained For example, send 1001010 using even parity For example, send 1001011 using even parity

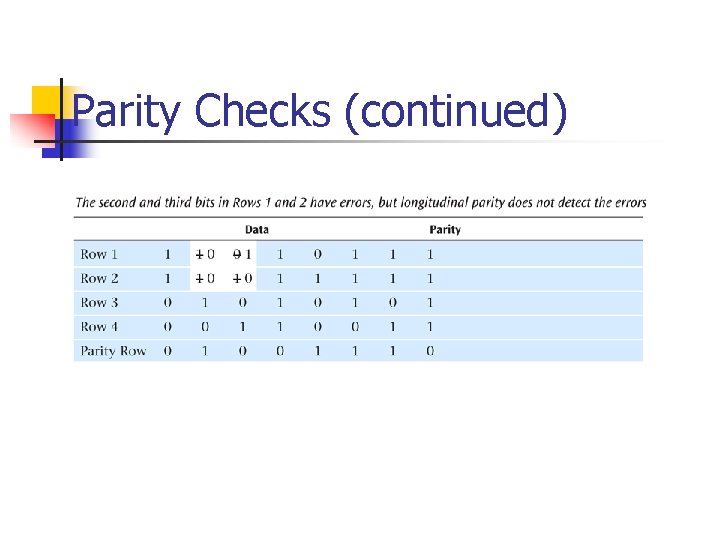
Parity Checks (continued) n Simple parity (continued) n What happens if the character 10010101 is sent and the first two 0 s accidentally become two 1 s? n n Thus, the following character is received: 11110101 Will there be a parity error? n Problem: Simple parity only detects odd numbers of bits in error

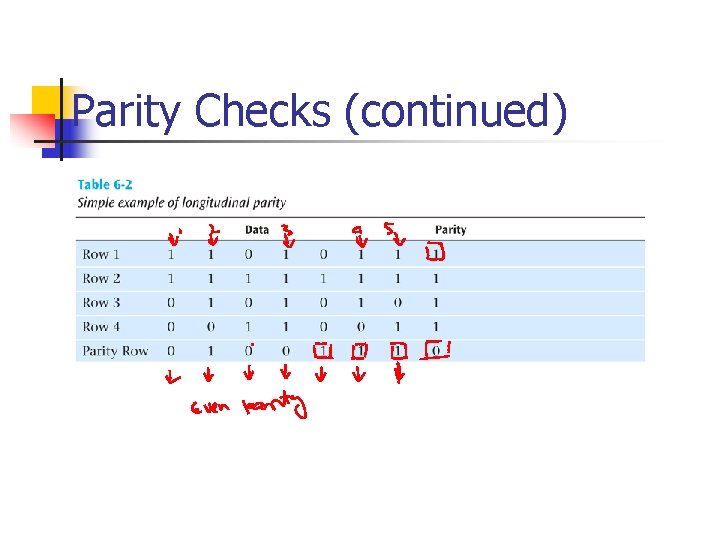
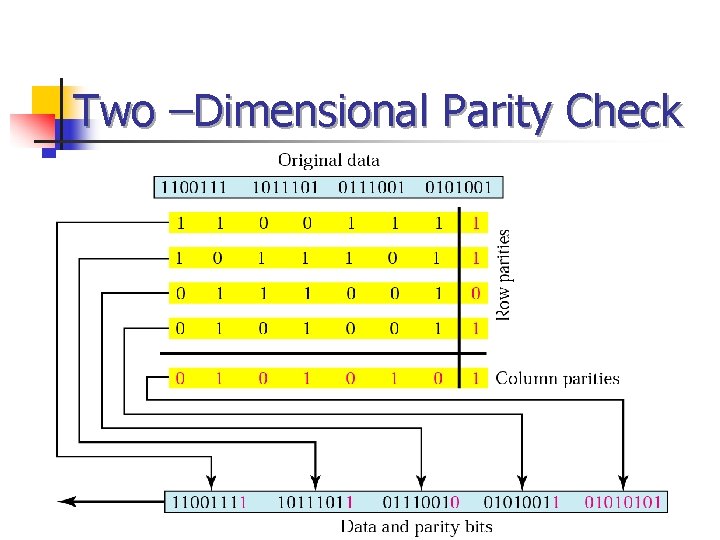
Parity Checks (continued) n Longitudinal parity n n n Adds a parity bit to each character then adds a row of parity bits after a block of characters The row of parity bits is actually a parity bit for each “column” of characters The row of parity bits plus the column parity bits add a great amount of redundancy to a block of characters

Parity Checks (continued)

Parity Checks (continued)

Parity Checks (continued) n n Both simple parity and longitudinal parity do not catch all errors Simple parity only catches odd numbers of bit errors Longitudinal parity is better at catching errors but requires too many check bits added to a block of data We need a better error detection method n What about arithmetic checksum?

19

Detection -examples Example 1 Suppose the sender wants to send the word world. In ASCII the five characters are coded as 11101111 1110010 1101100100 The following shows the actual bits sent 1110 110111100100 11011000 11001001

Detection – examples Example 2 Now suppose the word world in Example 1 is received by the receiver without being corrupted in transmission. 1110 110111100100 11011000 11001001 The receiver counts the 1 s in each character and comes up with even numbers (6, 6, 4, 4, 4). The data are accepted.

Detection – examples Example 3 Now suppose the word world in Example 1 is corrupted during transmission. 11111110 110111101100 11011000 11001001 The receiver counts the 1 s in each character and comes up with even and odd numbers (7, 6, 5, 4, 4). The receiver knows that the data are corrupted, discards them, and asks for retransmission.

Two –Dimensional Parity Check

Detection - example Example 4 Suppose the following block is sent: 10101001 00111001 1101 11100111 1010 However, it is hit by a burst noise of length 8, and some bits are corrupted. 10100011 10001001 1101 11100111 1010 When the receiver checks the parity bits, some of the bits do not follow the even-parity rule and the whole block is discarded. 10100011 10001001 1101 11100111 1010

25

Parity Codes n n To construct an even-parity code, add a parity bit such that the total number of 1 s is even. Information bits Even-parity code Odd-parity code 000 0 000 1 001 0 010 1 010 0 011 1 100 0 101 1 110 0 110 1 111 0 1 -bit parity codes can detect single bit errors, but they do not detect 2 bit errors.

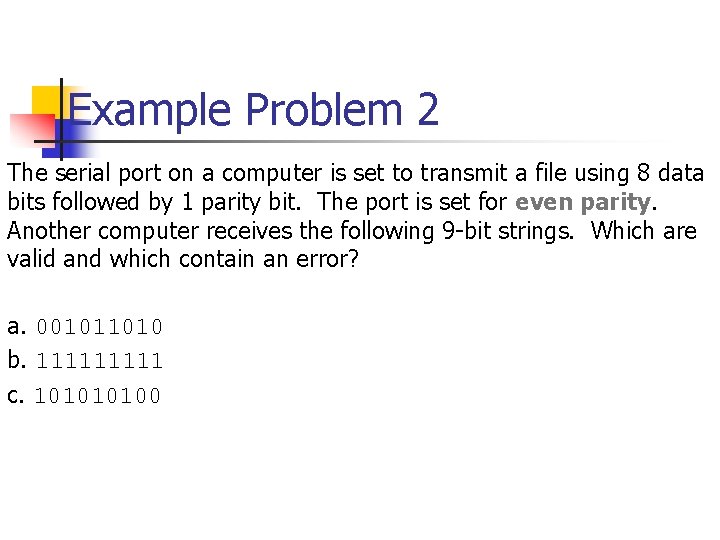
Example Problem 2 The serial port on a computer is set to transmit a file using 8 data bits followed by 1 parity bit. The port is set for even parity. Another computer receives the following 9 -bit strings. Which are valid and which contain an error? a. 001011010 b. 11111 c. 10100

Example Problem 2 -Solution The serial port on a computer is set to transmit a file using 8 data bits followed by 1 parity bit. The port is set for even parity. Another computer receives the following 9 bit strings. Which are valid and which contain an error? a. 001011010 even # of 1 s, no error b. 11111 odd # of 1 s, error c. 10100 even # of 1 s, no error

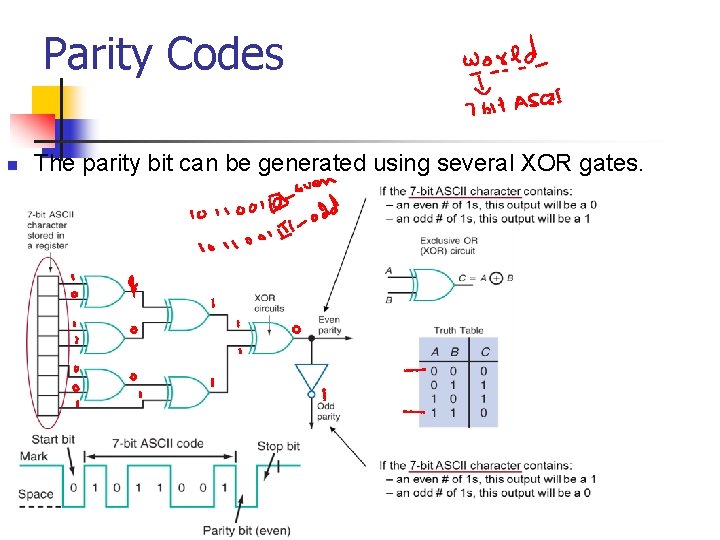
Parity Codes n The parity bit can be generated using several XOR gates.

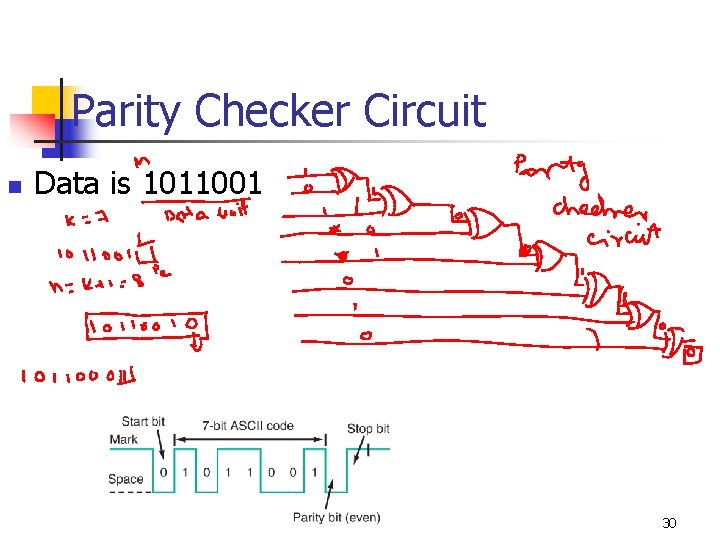
Parity Checker Circuit n Data is 1011001 30

Parity Bit Q: - What is a parity bit? n Ans: - A parity bit appended to an array of binary digits to make the sum of all the binary digits, including the parity bit, always odd (odd parity) or always even (even parity). 31

CRC Q: - What is the CRC? 32

Error Detection n Detection methods

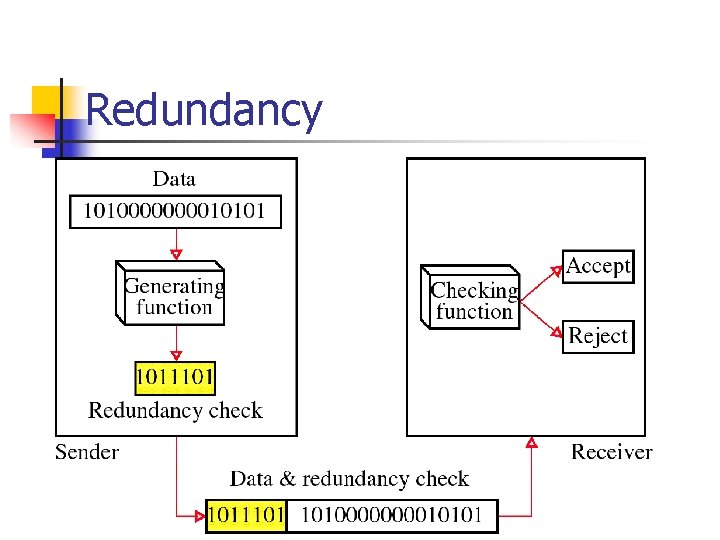
Redundancy

Four Types of Redundancy Checks are Used in Data Communications

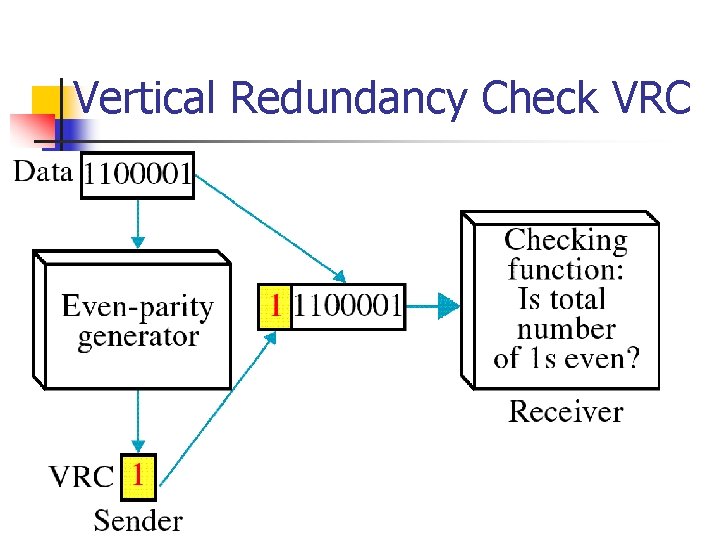
Vertical Redundancy Check VRC

Performance n n It can detect single bit error It can detect burst errors only if the total number of errors is odd.

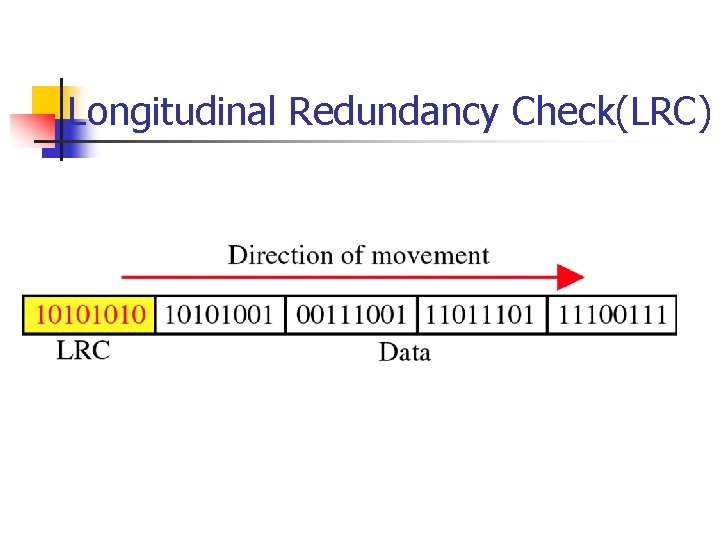
Longitudinal Redundancy Check(LRC)

Performance n n LRC increases the likelihood of detecting burst errors. If two bits in one data units are damaged and two bits in exactly the same positions in another data unit are also damaged, the LRC checker will not detect an error

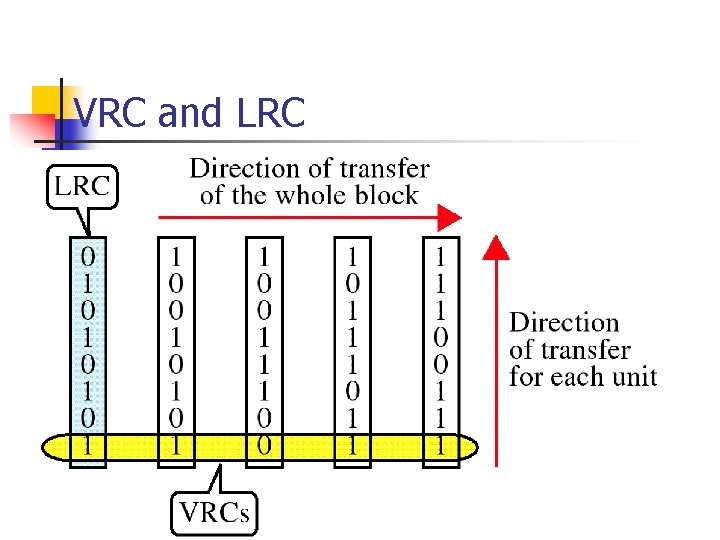
VRC and LRC

Cyclic Redundancy Check (CRC)

Cyclic Redundancy Check n n Given a k-bit frame or message, the transmitter generates an n-bit sequence, known as a frame check sequence (FCS), so that the resulting frame, consisting of (k+n) bits, is exactly divisible by some predetermined number. The receiver then divides the incoming frame by the same number and, if there is no remainder, assumes that there was no error.

Binary Division

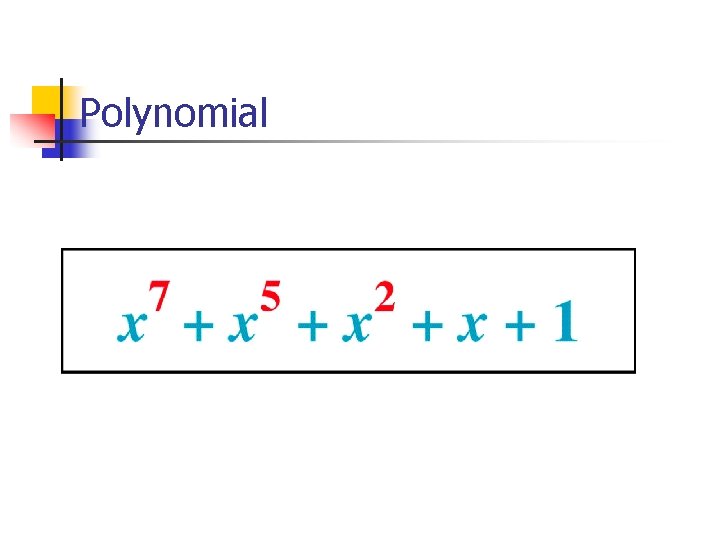
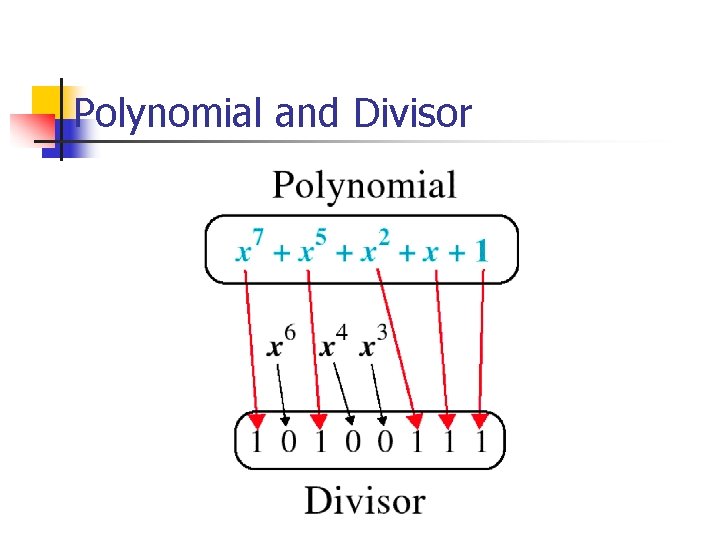
Polynomial

Polynomial and Divisor

Standard Polynomials

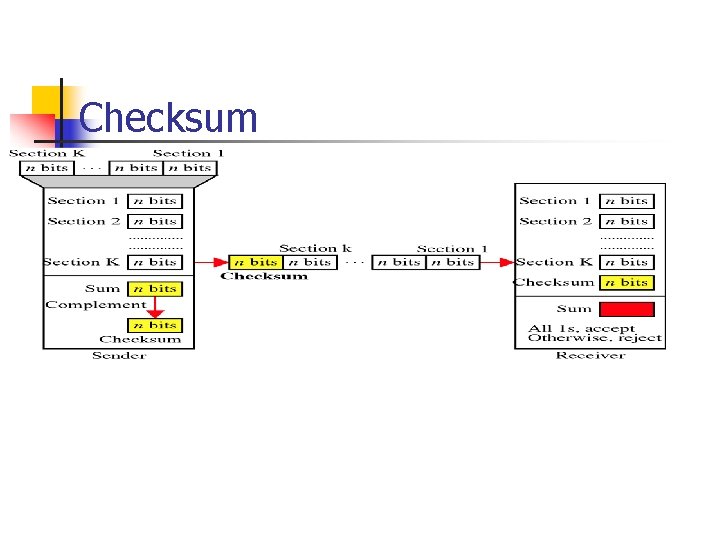
Checksum

At the Sender n n The unit is divided into k sections, each of n bits. All sections are added together using one’s complement to get the sum. The sum is complemented and becomes the checksum. The checksum is sent with the data

At the Receiver n n The unit is divided into k sections, each of n bits. All sections are added together using one’s complement to get the sum. The sum is complemented. If the result is zero, the data are accepted: otherwise, they are rejected.

Performance n n n The checksum detects all errors involving an odd number of bits. It detects most errors involving an even number of bits. If one or more bits of a segment are damaged and the corresponding bit or bits of opposite value in a second segment are also damaged, the sums of those columns will not change and the receiver will not detect a problem.

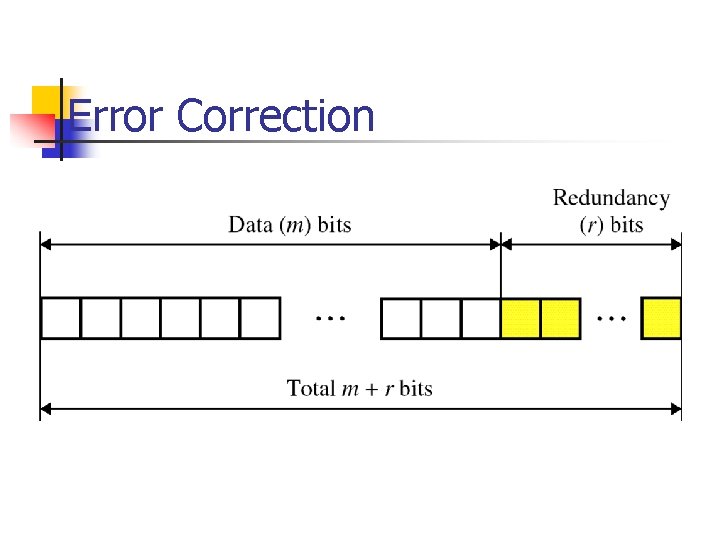
Error Correction It can be handled in two ways: n receiver can have the sender retransmit the entire data unit. n The receiver can use an error-correcting code, which automatically corrects certain errors.

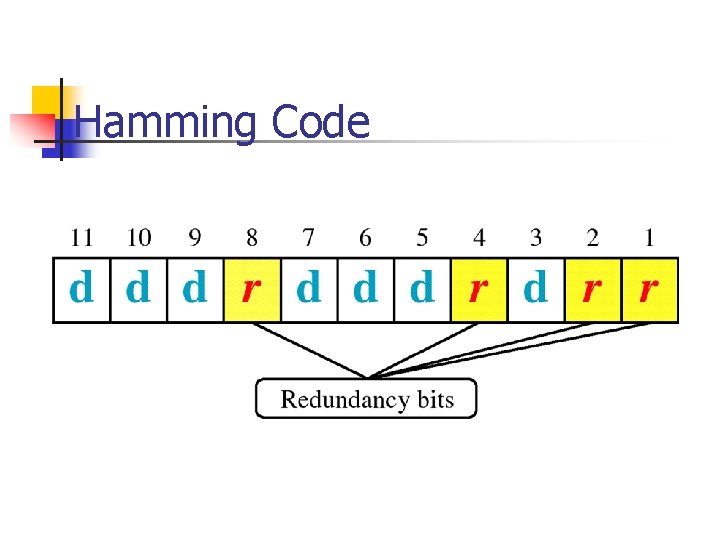
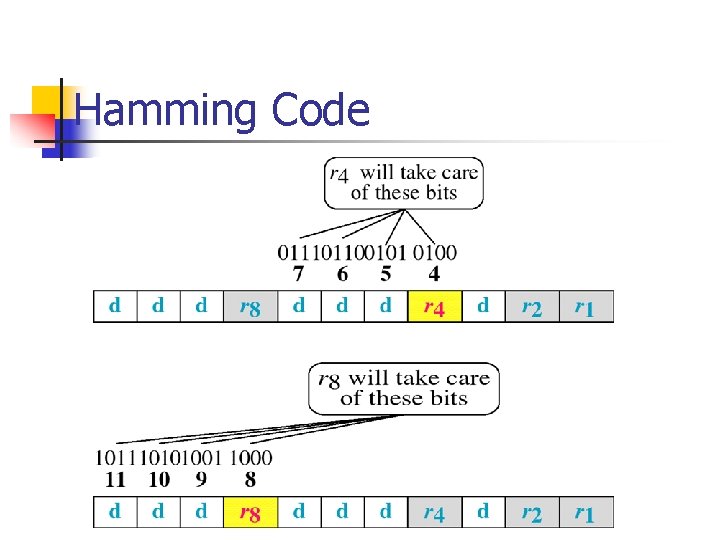
Single-bit Error Correction To correct an error, the receiver reverses the value of the altered bit. To do so, it must know which bit is in error. Number of redundancy bits needed n n Let data bits = m Redundancy bits = r Total message sent = m+r The value of r must satisfy the following relation: 2 r ≥ m+r+1

Error Correction

Hamming Code

Hamming Code

Hamming Code

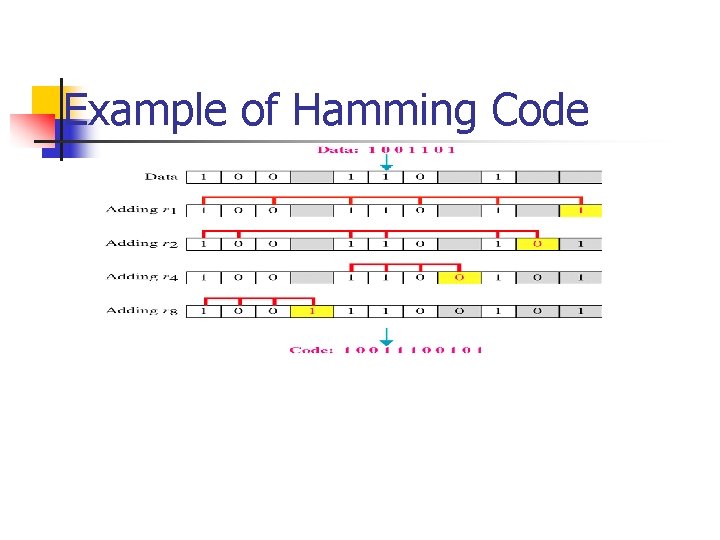
Example of Hamming Code

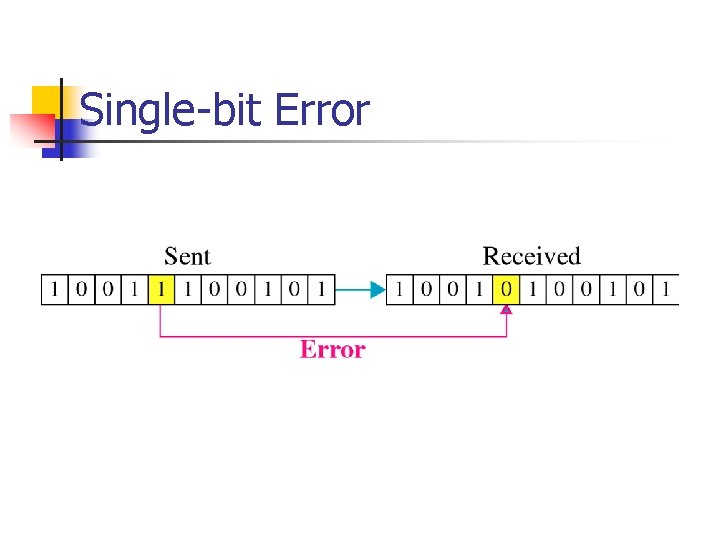
Single-bit Error

Error Detection

Hamming Distance Calculation Step - Ensure the two strings are of equal length. The Hamming distance can only be calculated between two strings of equal length. String 1: "1001 0010 1101" String 2: "1010 0010" n Step 2 - Compare the first two bits in each string. If they are the same, record a "0" for that bit. If they are different, record a "1" for that bit. In this case, the first bit of both strings is "1, " so record a "0" for the first bit. n Step 3 - Compare each bit in succession and record either "1" or "0" as appropriate. String 1: "1001 0010 1101" String 2: "1010 0010" Record: "0011 0000 1111" n Step 4 - Add all the ones and zeros in the record together to obtain the Hamming distance = 0+0+1+1+0+0+1+1 = 6 Tip: -If using a computer, "XOR" can be used to compare the two strings and obtain the "record. " n 60

CRC Q: - What is the CRC? n Ans: - The CRC is an error detecting code in which the code is the remainder resulting from dividing the bits to be checked by a predetermined binary number. 61

62

CRC Vs. Parity Q: - The CRC is an error detecting code in which the code is the remainder resulting from dividing the bits to be checked by a predetermined binary number. 63

CRC Vs. Parity Q: - The CRC is an error detecting code in which the code is the remainder resulting from dividing the bits to be checked by a predetermined binary number. n Ans: - The CRC has more bits and therefore provides more redundancy. That is, it provides more information that can be used to detect errors. 64

65

CRC Algorithm Q: - List three different ways in which the CRC algorithm can be described. 66

Cyclic Redundancy Check (CRC) n n Burst errors will most likely go undetected by a simple parity check scheme Instead, a more elaborate technique called Cyclic Redundancy Check (CRC) is typically implemented CRC appends redundant bits to the frame trailer called Frame Check Sequence (FCS) n FCS is later utilized at RX for error detection In a given frame containing n bits, we define: n k = number of original data bits n (n – k) = number of bits in the FCS field (i. e. additional bits) n So, that the total frame length is k + (n – k) = n bits 67

CRC Generation n n CRC generation is all about finding the FCS given the data (D) and a divisor (P) There are three equivalent ways to generate the CRC code: n Modulo-2 Arithmetic Method n Polynomial Method 68 n Digital Logic Method

Modulo 2 Arithmetic n n Binary arithmetic without carry Equivalent to XOR operation i. e: n 0 0 = 0; 1 0 = 1; 0 1 = 1; 1 1 = 0 n 1 0 = 0; 0 1 = 0; 1 1 = 1 Examples: 1010 +1010 ______ 0000 69

CRC Error Detection Process n n n Given k-bit data (D), the TX generates an (n – k)-bit FCS field (F) such that the total n-bit frame (T) is exactly divisible by some (nk+1)-bit predetermined devisor (P) (i. e. gives a zero remainder) In general, the received frame may or may not be equal, in value, to the sent frame n Let the received frame be (T’) n In error-free transmission T’ = T The RX then divides (T’) by the same known divisor (P) and checks if there is any remainder n If division yields a remainder then the frame is erroneous n If the division yields zero remainder then the frame is error-free unless many erroneous bits in T’ resulted in a new exact division by P n (This is very unlikely but possible, causing an undetected error!) 70

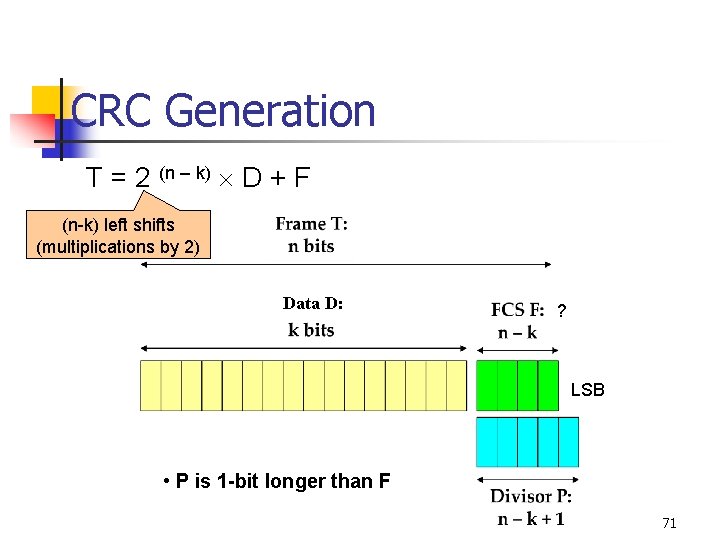
CRC Generation T = 2 (n – k) D + F (n-k) left shifts (multiplications by 2) Data D: ? LSB • P is 1 -bit longer than F 71

CRC Generation n T = 2(n – k) D + F, What is F that makes T divides P exactly ? Claim: F is the remainder obtained from dividing {2(n – k) D} by divisor P n where Q is the quotient and F is the remainder If this is the correct F, T should now divide P with Zero remainder n Note: For F to be a remainder when dividing by P, it should be 1 -bit smaller n 72

CRC Generation – Modulo-2 Arithmetic Method n At TX: CRC Generation (using previous rules): n n Multiply: 2(n – k) D (left shift by (n-k) bits) Divide: 2(n – k) D / P Use the resulting (n – k)-bit remainder as the FCS At RX: CRC Checking: RX divides the received T (i. e. T’) by the known divisor (P) and checks if there is any remainder 73

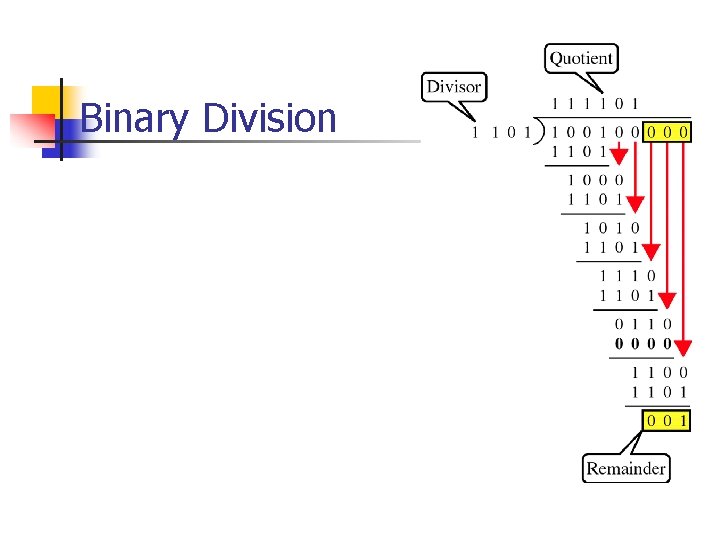
Example – Modulo-2 Arithmetic Method n Given n n D=1010001101 P=110101 Find the FCS field Solution: n First we note that: n n The size of the data block D is k = 10 bits The size of P is (n – k + 1) = 6 bits Hence the FCS length is n – k = 5 Total size of the frame T is n = 15 bits 74

Example – Modulo-2 Arith. Method n Solution (continued): n Multiply 2(n – k) D n n n 2(5) 1 0 0 0 1 1 0 1 = 1 0 0 0 1 1 0 0 0 This is a simple shift to the left by five positions Divide 2(n – k) D / P (see next slide for details) n 1 0 0 0 1 1 0 0 0 ÷ 1 1 0 1 yields: n n Quotient Remainder Q=1101010110 R=01110 So, FCS = R = 0 1 1 1 0: Append it to D to get the full frame T to be transmitted T=101000110101110 M FCS 75

Example – Modulo 2 Arith. Method # of bits < # of bits in P, result of division is 0 Checks you should do (exercise): = FCS = F - Verify correct operation, i. e. that 2(n-k)D = P*Q + R - Verify that obtained T (101000110101110) divides P (110101) exactly 76 (i. e. with zero remainder)