Least Squares Curves Rational Representations Splines and Continuity


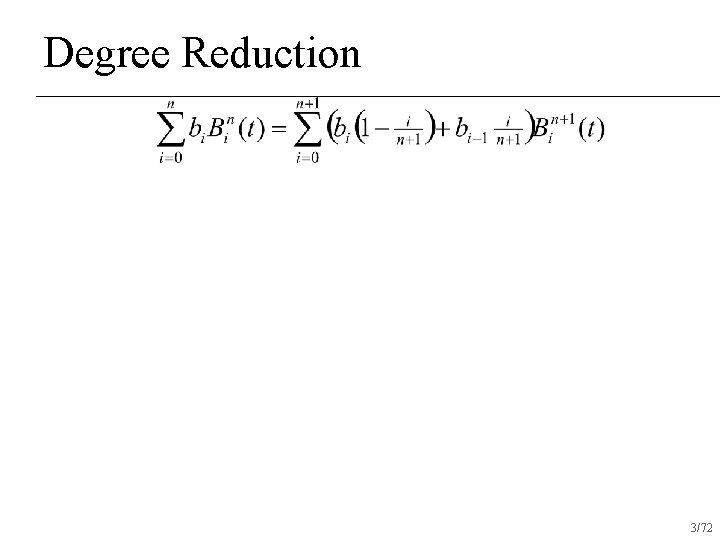
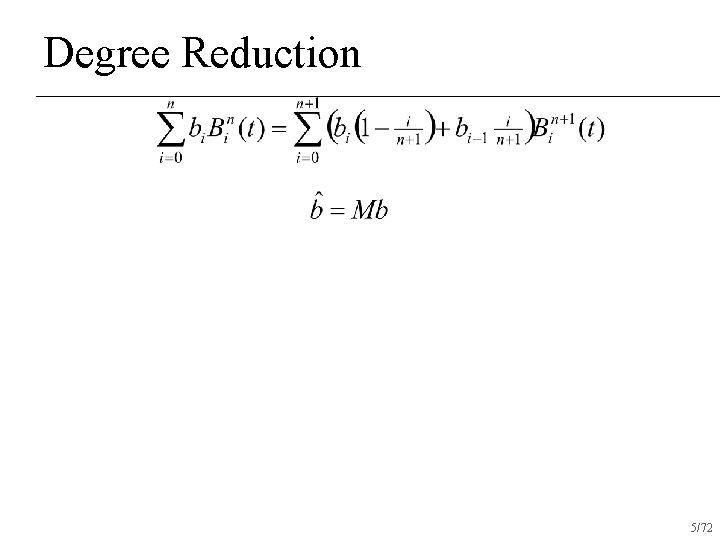
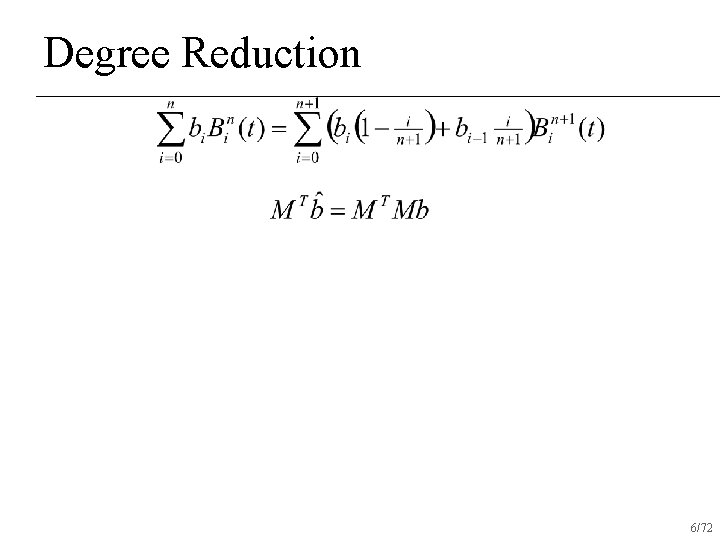
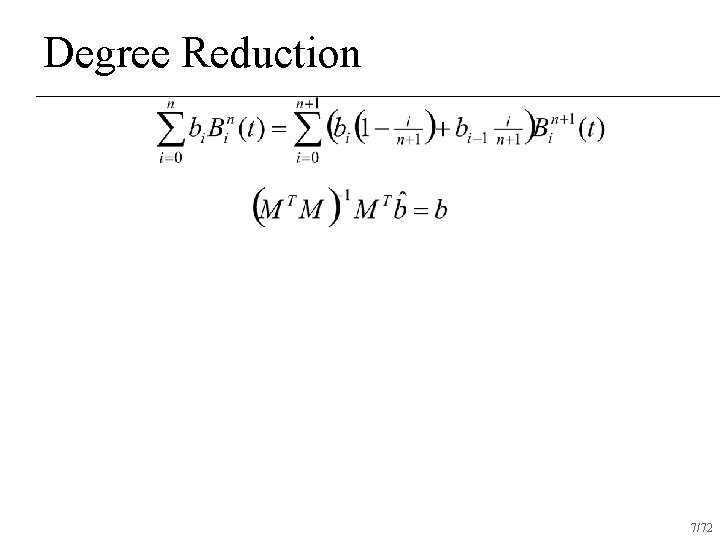
































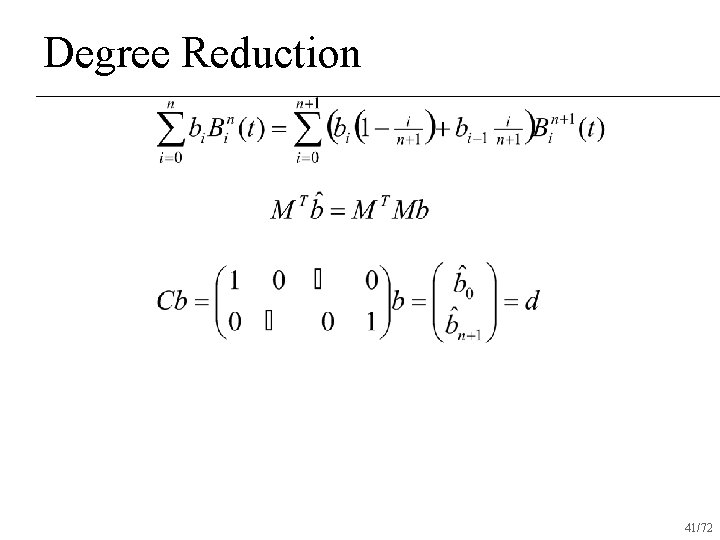
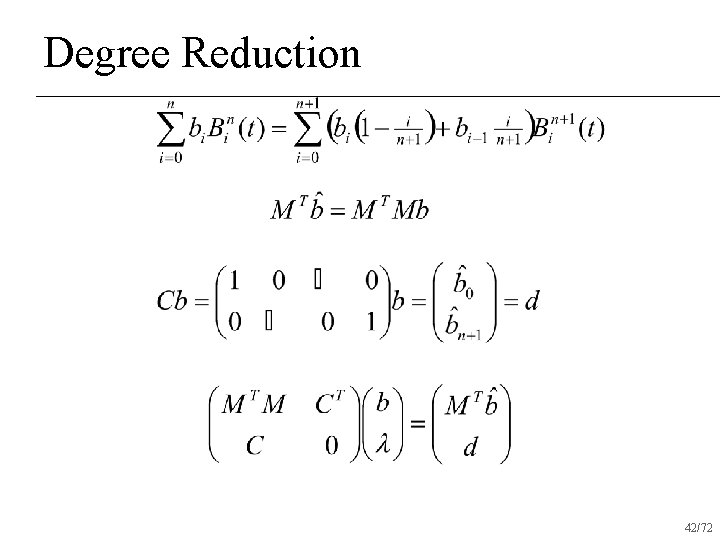






















- Slides: 72

Least Squares Curves, Rational Representations, Splines and Continuity Dr. Scott Schaefer 1

Degree Reduction n Given a set of coefficients for a Bezier curve of degree n+1, find the best set of coefficients of a Bezier curve of degree n that approximate that curve 2/72
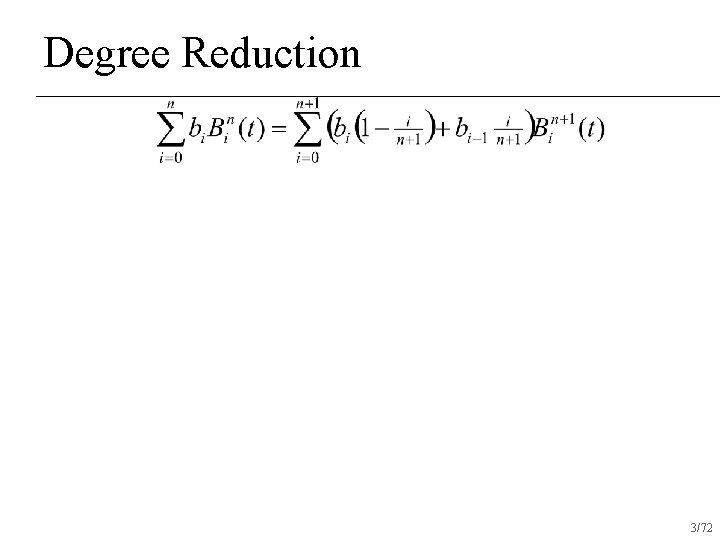
Degree Reduction 3/72

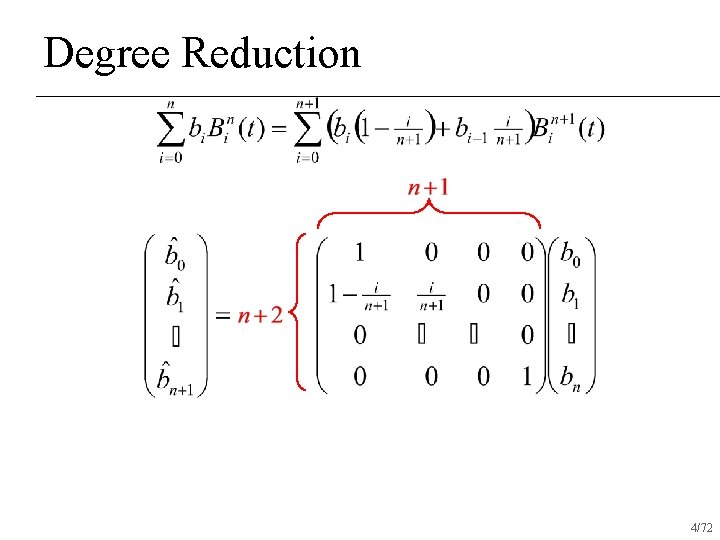
Degree Reduction 4/72
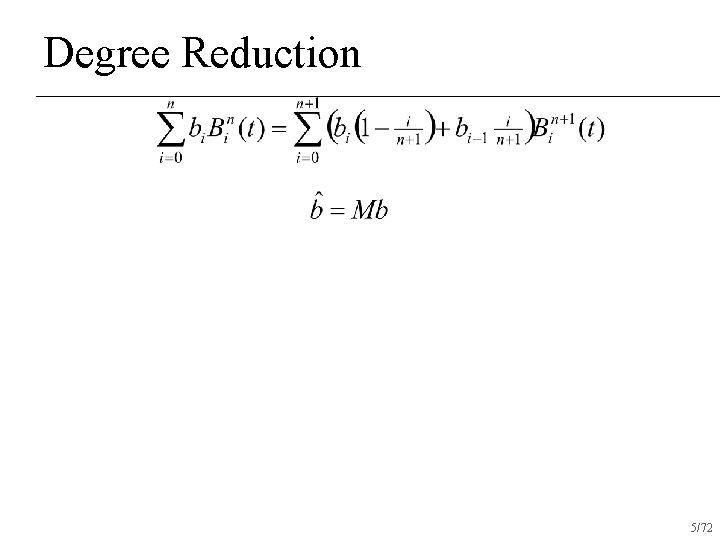
Degree Reduction 5/72
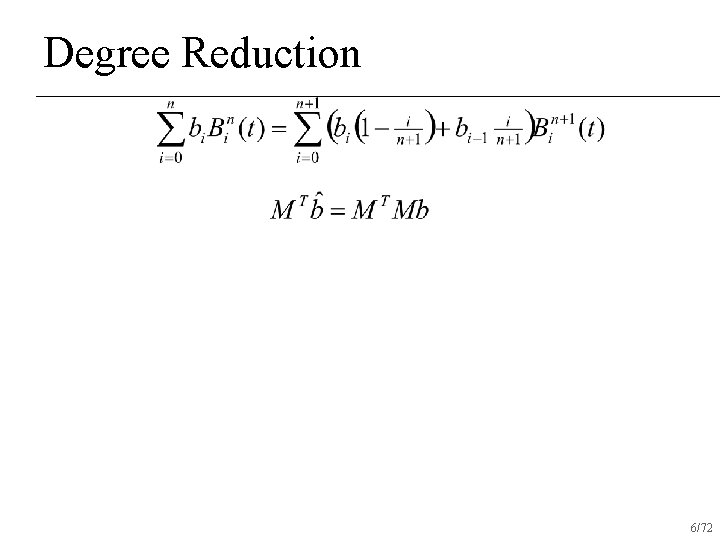
Degree Reduction 6/72
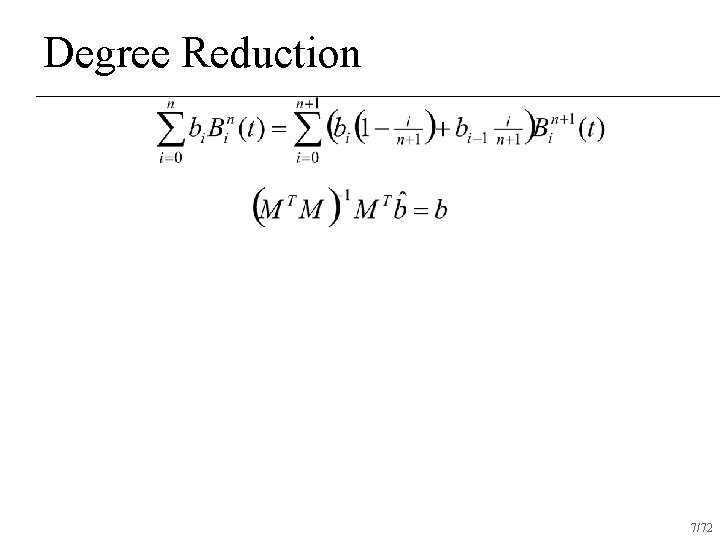
Degree Reduction 7/72

Degree Reduction n Problem: end-points are not interpolated 8/72

Least Squares Optimization 9/72

Least Squares Optimization 10/72

Least Squares Optimization 11/72

Least Squares Optimization 12/72

Least Squares Optimization 13/72

Least Squares Optimization 14/72

The Pseudo. Inverse n What happens when isn’t invertible? 15/72

The Pseudo. Inverse n What happens when isn’t invertible? 16/72

The Pseudo. Inverse n What happens when isn’t invertible? 17/72

The Pseudo. Inverse n What happens when isn’t invertible? 18/72

The Pseudo. Inverse n What happens when isn’t invertible? 19/72

The Pseudo. Inverse n What happens when isn’t invertible? 20/72

The Pseudo. Inverse n What happens when isn’t invertible? 21/72

The Pseudo. Inverse n What happens when isn’t invertible? 22/72

The Pseudo. Inverse n What happens when isn’t invertible? 23/72

The Pseudo. Inverse n What happens when isn’t invertible? 24/72

The Pseudo. Inverse n What happens when isn’t invertible? 25/72

The Pseudo. Inverse n What happens when isn’t invertible? 26/72

The Pseudo. Inverse n What happens when isn’t invertible? 27/72

The Pseudo. Inverse n What happens when isn’t invertible? 28/72

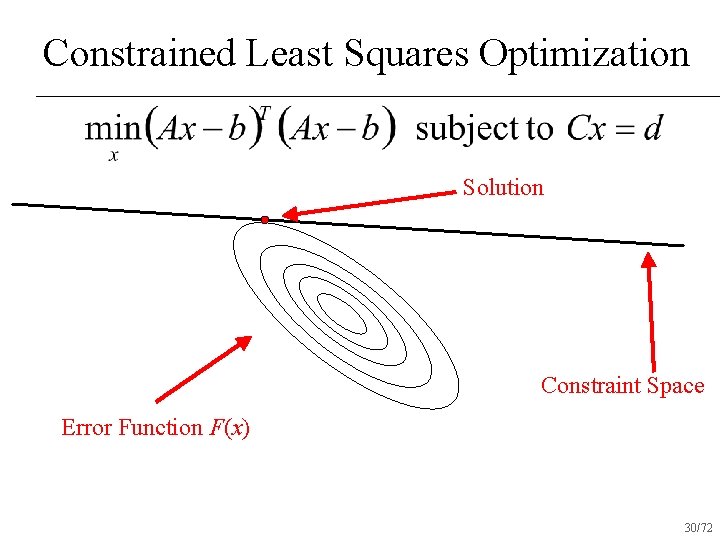
Constrained Least Squares Optimization 29/72

Constrained Least Squares Optimization Solution Constraint Space Error Function F(x) 30/72

Constrained Least Squares Optimization 31/72

Constrained Least Squares Optimization 32/72

Constrained Least Squares Optimization 33/72

Constrained Least Squares Optimization 34/72

Constrained Least Squares Optimization 35/72

Least Squares Curves 36/72

Least Squares Curves 37/72

Least Squares Curves 38/72

Least Squares Curves 39/72

Degree Reduction n Problem: end-points are not interpolated 40/72
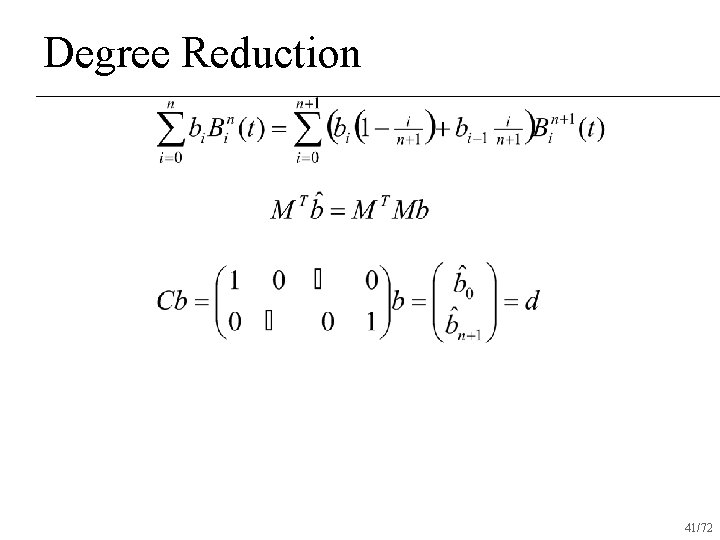
Degree Reduction 41/72
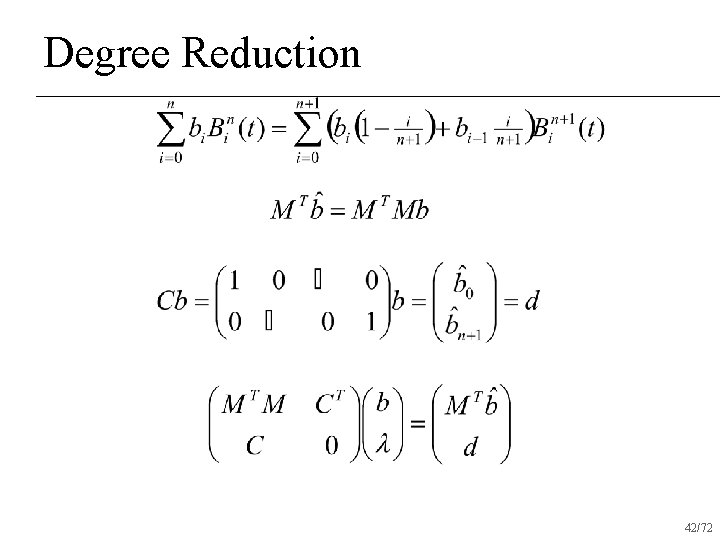
Degree Reduction 42/72

Rational Curves n Curves defined in a higher dimensional space that are “projected” down 43/72

Rational Curves n Curves defined in a higher dimensional space that are “projected” down 44/72

Rational Curves n Curves defined in a higher dimensional space that are “projected” down 45/72

Rational Curves n Curves defined in a higher dimensional space that are “projected” down 46/72

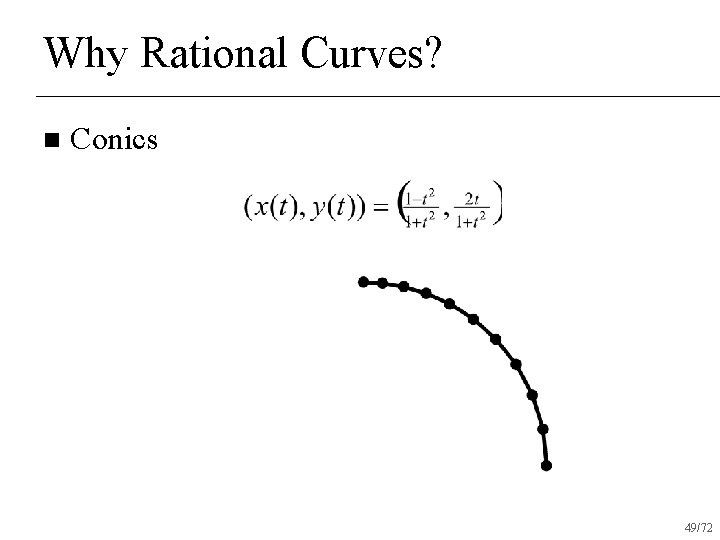
Why Rational Curves? n Conics 47/72

Why Rational Curves? n Conics 48/72

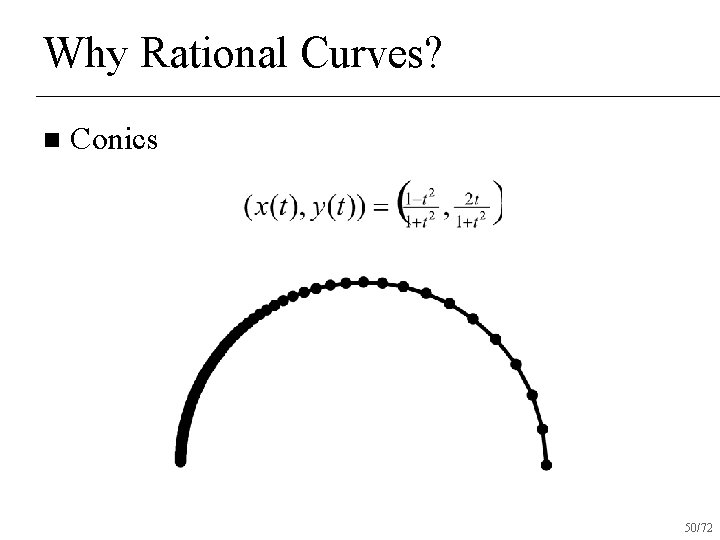
Why Rational Curves? n Conics 49/72

Why Rational Curves? n Conics 50/72

Derivatives of Rational Curves 51/72

Derivatives of Rational Curves 52/72

Derivatives of Rational Curves 53/72

Derivatives of Rational Curves 54/72

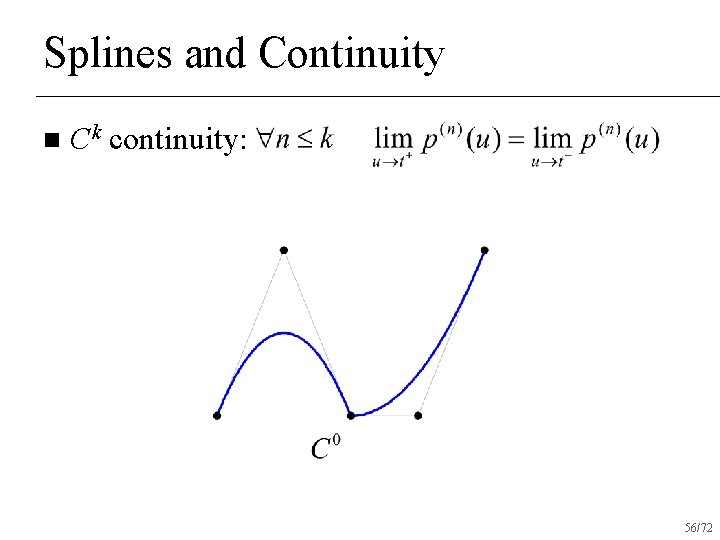
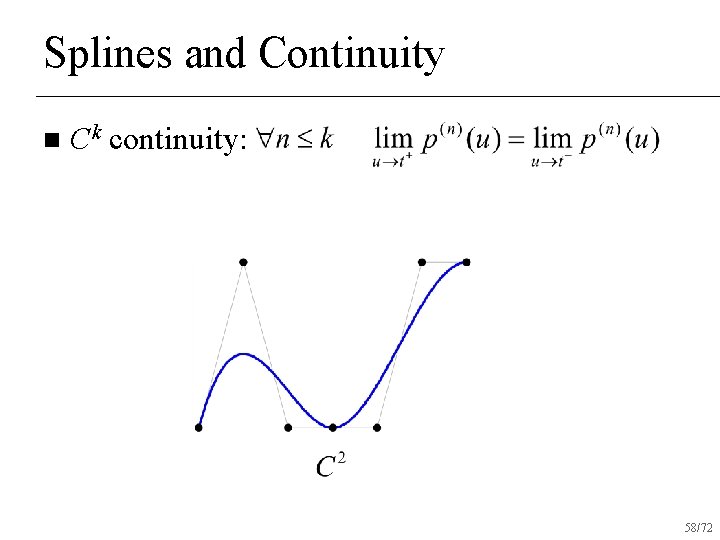
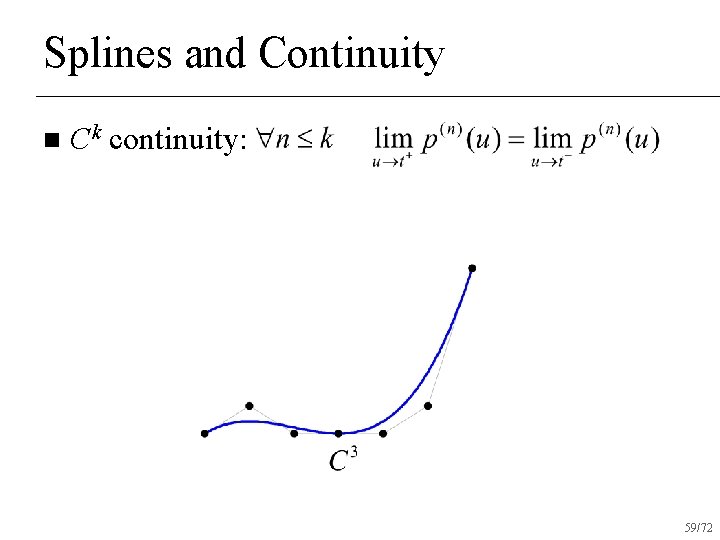
Splines and Continuity n Ck continuity: 55/72

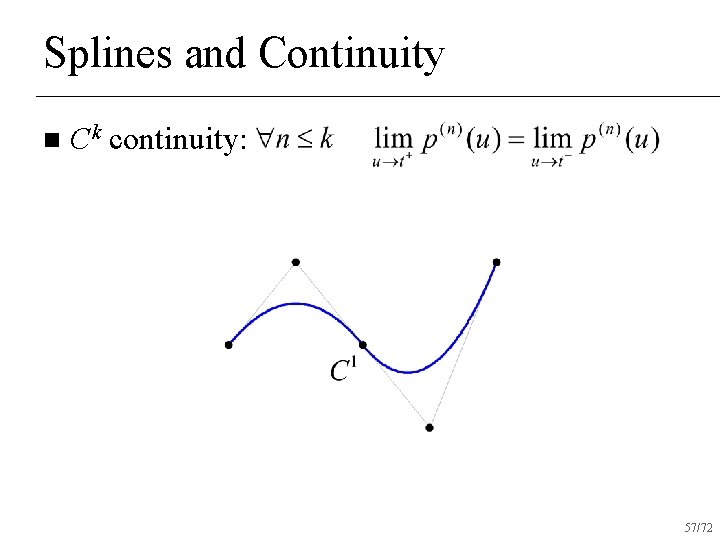
Splines and Continuity n Ck continuity: 56/72

Splines and Continuity n Ck continuity: 57/72

Splines and Continuity n Ck continuity: 58/72

Splines and Continuity n Ck continuity: 59/72

Splines and Continuity n Assume two Bezier curves with control points p 0, …, pn and q 0, …, qm 60/72

Splines and Continuity n Assume two Bezier curves with control points p 0, …, pn and q 0, …, qm n C 0: pn=q 0 61/72

Splines and Continuity n Assume two Bezier curves with control points p 0, …, pn and q 0, …, qm C 0: pn=q 0 n C 1: n(pn-pn-1)=m(q 1 -q 0) n 62/72

Splines and Continuity n Assume two Bezier curves with control points p 0, …, pn and q 0, …, qm C 0: pn=q 0 n C 1: n(pn-pn-1)=m(q 1 -q 0) n C 2: n(n-1)(pn-2 pn-1+pn-2)=m(m-1)(q 0 -2 q 1+q 2) n… n 63/72

Splines and Continuity n Geometric Continuity u A curve is Gk if there exists a reparametrization such that the curve is Ck 64/72

Splines and Continuity n Geometric Continuity u A curve is Gk if there exists a reparametrization such that the curve is Ck 65/72

Splines and Continuity n Geometric Continuity u A curve is Gk if there exists a reparametrization such that the curve is Ck 66/72

Problems with Bezier Curves More control points means higher degree n Moving one control point affects the entire curve n 67/72

Problems with Bezier Curves More control points means higher degree n Moving one control point affects the entire curve n 68/72

Problems with Bezier Curves More control points means higher degree n Moving one control point affects the entire curve n Solution: Use lots of Bezier curves and maintain Ck continuity!!! 69/72

Problems with Bezier Curves More control points means higher degree n Moving one control point affects the entire curve n Solution: Use lots of Bezier curves and maintain Ck continuity!!! Difficult to keep track of all the constraints. 70/72

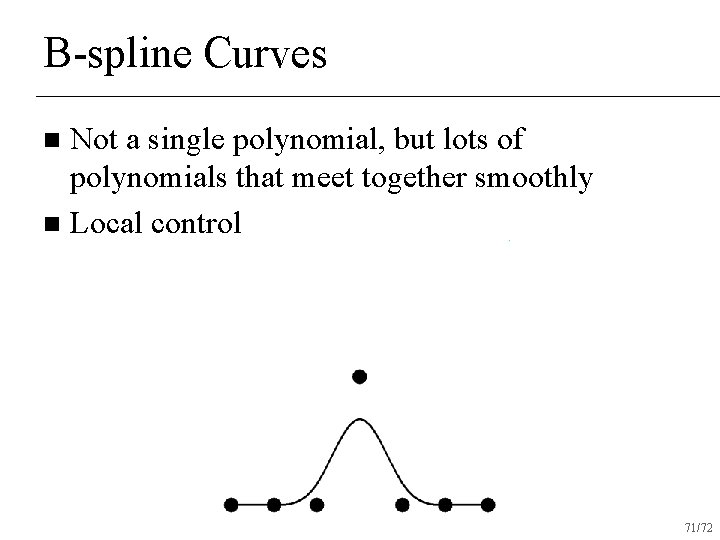
B-spline Curves Not a single polynomial, but lots of polynomials that meet together smoothly n Local control n 71/72

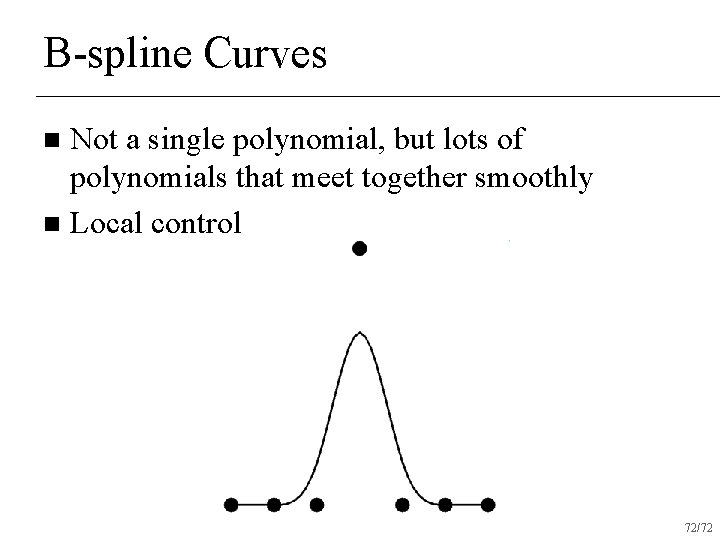
B-spline Curves Not a single polynomial, but lots of polynomials that meet together smoothly n Local control n 72/72