WITHOUT COUNTING THE SQUARES HOW MANY ARE SHADED

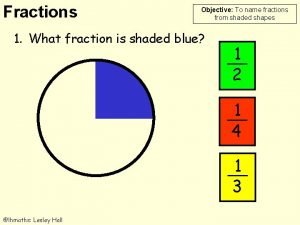
WITHOUT COUNTING THE SQUARES, HOW MANY ARE SHADED? EXPLAIN HOW YOU ARRIVED AT YOUR COUNT.

WHICH OF THE FOLLOWING CAN YOU REPRESENT VISUALLY TO REPRESENT THE TOTAL OF 36 10 X 4 – 4 = 36 8 X 4 + 4 = 36 (10 X 10) – (8 X 8) = 36 10 + 9 X 2 + 8 = 36 2(10 + 8) = 36 2 X 10 + 2 X 8 = 36

Circle Fever CASE 1. HOW DO YOU SEE THE PATTERN 1 2 3 GROWING? 2. WHAT WOULD THE TENTH CASE LOOK LIKE? 3. HOW MANY CIRCLES WOULD BE IN THE 100 TH CASE? WHAT WOULD IT LOOK LIKE? 4. CAN YOU MODEL THE PATTERN WITH AN EXPRESSION?

Pyramids (Session 1 When completing a pyramid, each number above the base is made from Launch) the sum of the two supporting it. 1. Complete the pyramids. 2. Find the value of b for which the pyramid can be filled with whole numbers. Find at least 3 different pyramids using this b value. 3. Find at least 4 different pairs of possible values of x and y. How many solutions are possible? Write an expression that relates x and y

GOAL S Exposure to a variety of “tasks” (2 -5 per session) What course could you use them in? How could you use them? Source Websites Resources to go (10 -12) Powerpoint posted on webpage until school starts (or email request) First 3 Days (for INT I and INT III)

Hollow Squares (Session 2 Launch) In Napoleanic battles a hollow square was a popular formation for an infantry battalion designed to cope with Cavalry charges. Below are 2 diagrams showing symmetrical hollow square formations. 1. Explain two different methods to find the number of dots in each. 2. A general has 960 soldiers. How many different ways cans he arrange his battalion in a symmetric hollow square?

Reach 100 (S 1) You must choose four different digits from 1 -9 to put in a 2 x 2 grid {example shown right}: This gives four two-digit numbers 52 (first row) 19 (second row) 51 (left column) 29 (right column) With a SUM of 151. Your challenge is to find four different digits that give four two digit numbers which have a sum of 100. How many ways can you find of doing it? Also, explain a way to tell if the total is going to be odd or even 5 2 1 9

Reach 200 (S 2) Choose any four digits from 0 -9 to put in a 2 x 2 grid {example shown right}: This gives four two-digit numbers 41 (first row) 26 (second row) 42 (left column) 16 (right column) With a SUM of 125. Is there a quick way to tell if the total is going to be odd or even? Your challenge is to make a sum of 200 {digits can be repeated}. How many ways can you find of doing it? If four 0 s are used, the sum would be 0 and if four 9 s were used 4 1 2 6

Overlap (Part 1: Seven Regions) (S 1) 1. Place the digits 1 to 7, one in each region, so that each circle has the same total. Can you also show that A) You cannot have a circle total of 16 with a 4 in the center? B) You cannot have circle totals greater than 19 or less than 13? C) For a circle total of 13, you cannot have anything other than a 1 in the center

Overlap (Part 2: Nine Regions) (S 2) 1. Place the digits 1 to 9, one in each region, so that the sum of the numbers within each ring is the same. 2. Can you find more than one solution? 3. Can you find the lower and upper bound for the possible ring totals? 4. Is there a solution for each ring total between the upper and lower bounds? If not, can you prove that no solution exists?

DATA CHALLENGES (S 1 & S 2) 1. The mean, median, mode are all 5 in the set: 2, 5, 5, 6, 7. Can you find other sets of 5 positive whole numbers where the mean = median = mode = range 2. Can you find sets of five positive whole numbers that satisfy the following properties: A) mode < median < mean B) mode < mean < median C) mean < mode < median D) mean < median < mode E) median < mean < mode F) median < mean < mode Not all of these can be satisfied by sets of five numbers, can you explain why? 3. Show that some of them can be satisfied with sets of just 4 numbers.

Resource Sites: #1) https: //www. youcubed. org/tasks/ organized by concepts, grades, mathematical practices and topics #2) https: //nrich. maths. org/ great source for tasks (habits of minds) and interactives Shifting Times Tables: https: //nrich. maths. org/6713 Arithmagons: https: //nrich. maths. org/2670 Route to Infinity: https: //nrich. maths. org/5469 Where Can we Visit? https: //nrich. maths. org/746 unusual Sudoku:

CHOICES Who will be in the second session? Choice 1: Short Problem (overlap) Choice 2: Long Problem(data challenge) Choice 3: Private time to review

GOAL S Exposure to a variety of “tasks” (5 -7) What course could you use them in? How could you use them? Source Websites Resources to go (10 -12) Powerpoint posted on webpage until school starts (or email request) First 3 Days (for INT I and INT III) If time/interested

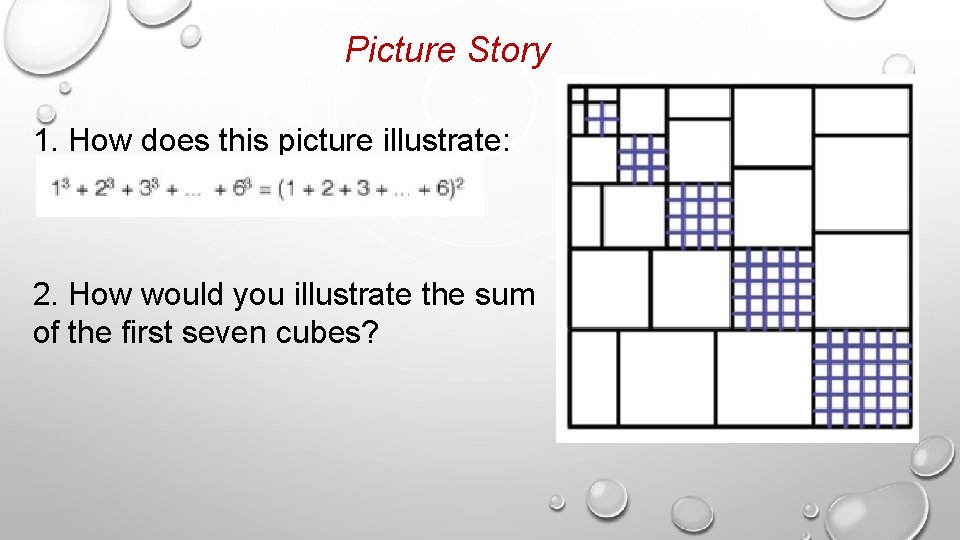
Picture Story 1. How does this picture illustrate: 2. How would you illustrate the sum of the first seven cubes?

FORWARDS ADD BACKWARDS The number 747 can be formed by adding a 3 -digit number with its reversal. 1. Find the other two ways of making 747 this way. 2. Which other numbers between 700 and 800 can be formed from the sum of a number and its reversal {there are more than five}? 3. How many numbers between 300 and 400 can be formed from the sum of a number and its reversal? Between 800 and 900? 4. The number 1251 can be formed by adding a 3 digit number with its reversal. Which other numbers between 1200 and 1300

WIPEOUT Take the numbers 1, 2, 3, 4, 5, 6 and choose one to wipe out. For example, if you wipe out 5, you are left with 1, 2, 3, 4, 6 and the mean is 3. 2. 1. Can you wipe out 1 number from 1 to 6 leaving behind a mean that is a whole number? 2. If you start with sets of numbers 1 to N, where N is even, which number can be wiped out so the mean of the remaining numbers is a whole number? What happens when N is odd? 3. One of the numbers from 1 to 6 is wiped out and the mean is 3. 6, what number was wiped out? 4. One of the numbers from 1 to N is wiped out and the mean is 6. 83, what is N and what number was wiped out?

Can They Be Equal? Charlie has been drawing rectangles. The first rectangle has a perimeter of 30 units and an area of 50 square units. The second has a perimeter of 24 units an area of 20 square units. 1) Charlie wonders if he can find a rectangle of side length 10 units whose area and perimeter have the same numerical value. Can you find a rectangle that satisfies this condition? 2) Can you find more examples of rectangles whose area and perimeter have the same value?

Leo the Rabbit is climbing up a flight of 10 steps. Leo can only hop up 1 or 2 steps each time he hops. He never hops down, only up. How many different ways can Leo hop up the flight of 10 steps? Provide evidence to justify you thinking. Broken Eggs An old woman goes to market and a horse steps on her basket and crushes the eggs. The rider offers to pay for damages and asks her how many eggs she has bought. She does not remember the exact number, but when she takes them out two at a time, there is 1 egg left. The same happened when she picked them out three, four, five and six at a time, but when she took them out seven at a time they came out even. What is the

Blue and White In the examples below, identical squares of side 1 unit contain some circles in blue. In which of the four examples is the shaded area the greatest? Explain and justify your answer.

FIVE NUMBERS Five numbers are added together in pairs to produce the following answers: 0, 2, 4, 4, 6, 8, 9, 11, 13, 15 ISOSCELES TRIANGLES An isosceles triangle with an area of 9 square cm has a vertex at (20, 20). If all vertices will have whole number coordinates, how many triangles can be formed? Be prepared to explain how you know that you have found all possible triangles.

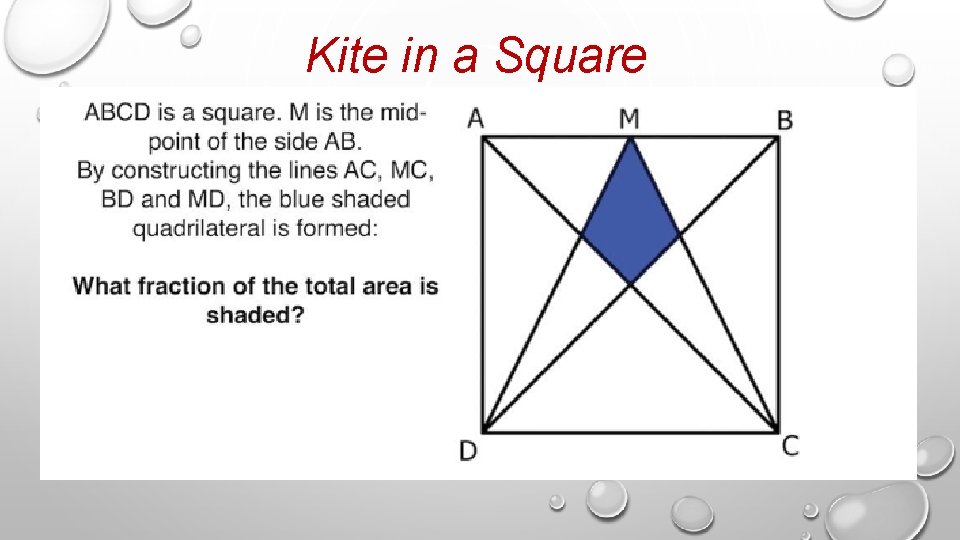
Kite in a Square