Packing squares in squares SASMS fall 2008 David

Packing squares in squares SASMS fall, 2008 David Rhee

1. Introduction • Packing circles has been studied by Gauss and Kepler since 1600’s • Axel Thue(1890) and Thomas Hales (1998) proved that the hexagonal packing is the densest of all possible sphere packings in 2 D and 3 D • Packing squares began to be studied recently (~1970)

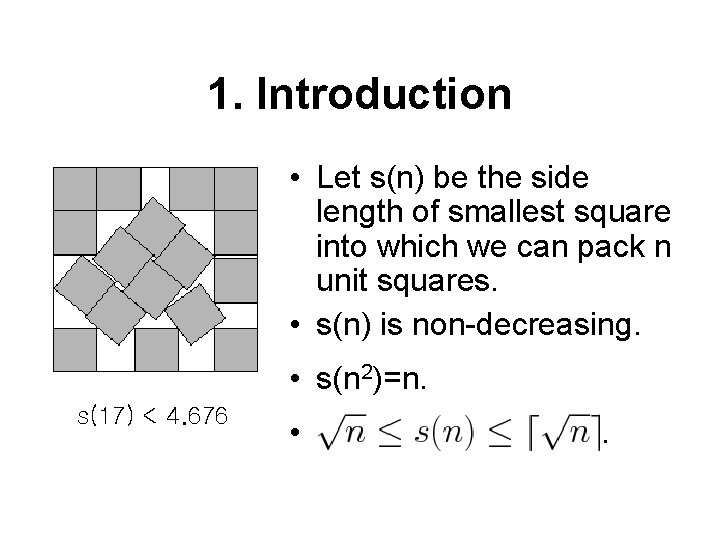
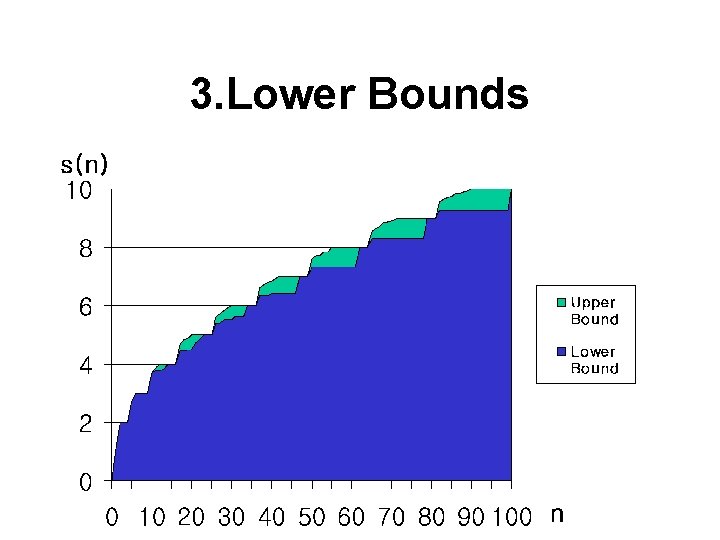
1. Introduction • Let s(n) be the side length of smallest square into which we can pack n unit squares. • s(n) is non-decreasing. • s(n 2)=n. s(17) < 4. 676 • .

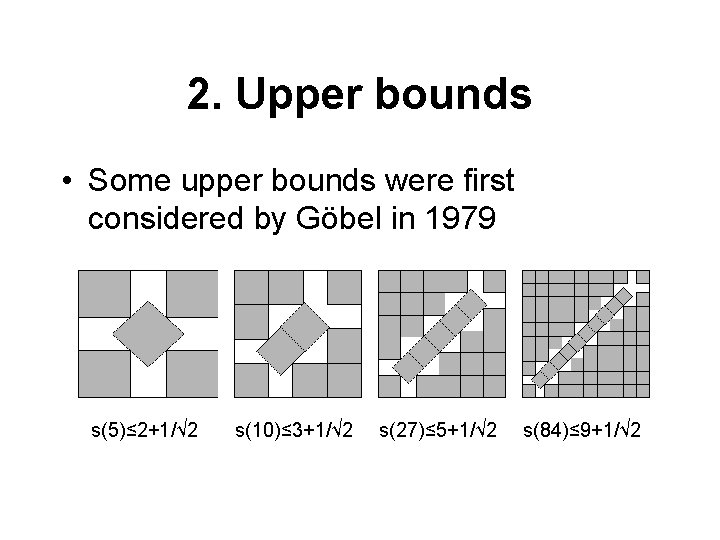
2. Upper bounds • Some upper bounds were first considered by Göbel in 1979 s(5)≤ 2+1/√ 2 s(10)≤ 3+1/√ 2 s(27)≤ 5+1/√ 2 s(84)≤ 9+1/√ 2

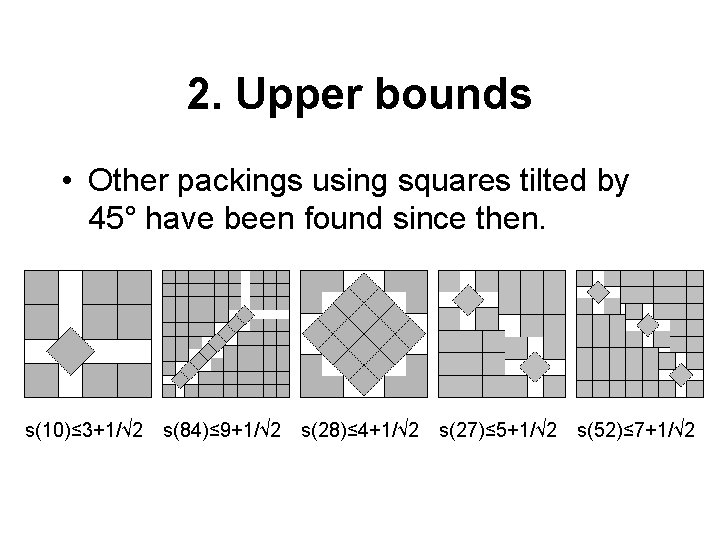
2. Upper bounds • Other packings using squares tilted by 45° have been found since then. s(10)≤ 3+1/√ 2 s(84)≤ 9+1/√ 2 s(28)≤ 4+1/√ 2 s(27)≤ 5+1/√ 2 s(52)≤ 7+1/√ 2

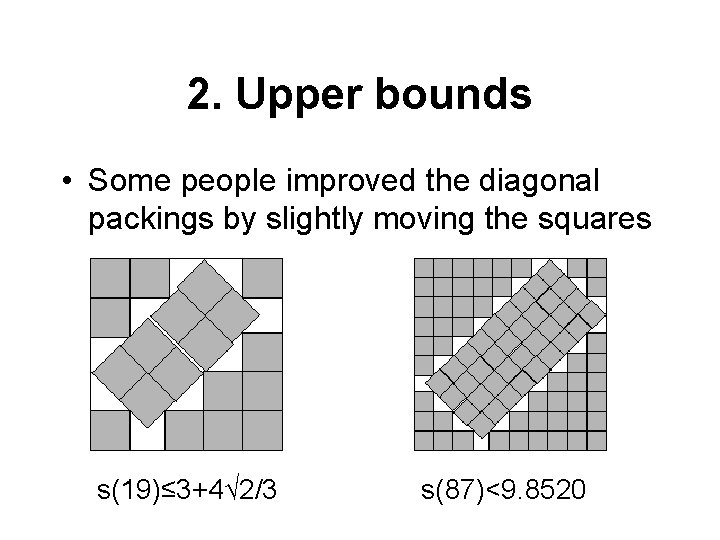
2. Upper bounds • Some people improved the diagonal packings by slightly moving the squares s(19)≤ 3+4√ 2/3 s(87)<9. 8520

2. Upper bounds • Generally, packings are more complicated. Many of these results were found by a new efficient algorithm found in 2005. s(11)<3. 8771 s(17)<4. 6756 s(29)≤ 5. 9344 s(68)≤ 15/2+√ 7/2 s(71)≤ 8. 9633

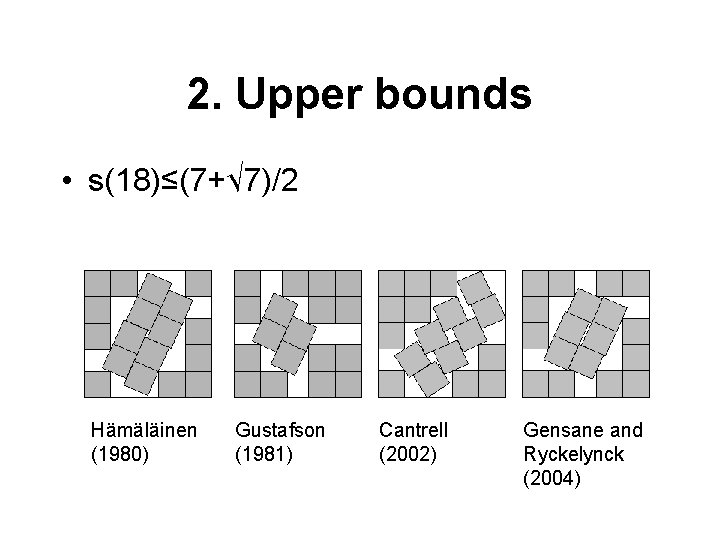
2. Upper bounds • s(18)≤(7+√ 7)/2 Hämäläinen (1980) Gustafson (1981) Cantrell (2002) Gensane and Ryckelynck (2004)

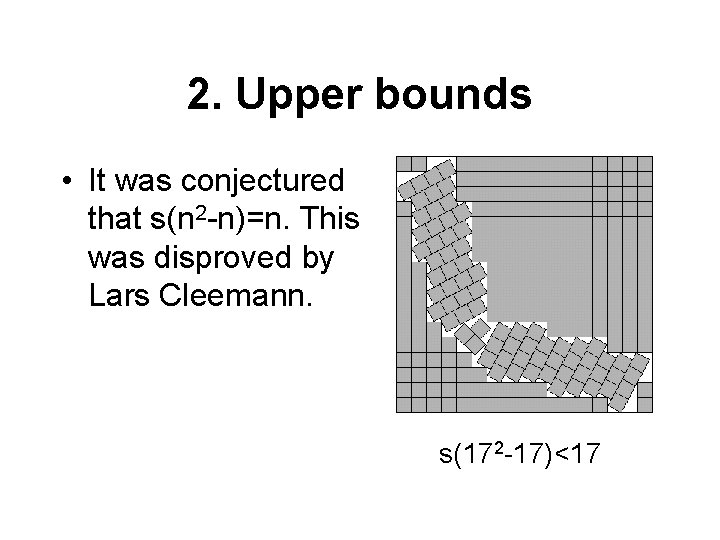
2. Upper bounds • It was conjectured that s(n 2 -n)=n. This was disproved by Lars Cleemann. s(172 -17)<17

2. Upper bounds • W(s): =s 2 -max{n: s(n)≤s}, then W(s) is O(s 7/11) (Erdös and Graham, 1975) • W(s)=O(s(3 -√ 3)/2+ε) for every ε>0 (Montgomery, 1978? ) • W(s) is not O(sα) when α<1/2 (Roth and Vaughan, 1978)

3. Lower bounds • Lemma 1. (corner) Any unit square inside the first quadrant whose center is in [0, 1]2 contains the point (1, 1). • Lemma 2. (edge) Let 0<x≤ 1, 0<y≤ 1, and x+2 y<2√ 2. Then any unit square inside the first quadrant whose center is contained in [1, 1+x]x[0, y] contains either the point (1, y) or the point (1+x, y).

3. Lower bounds • Lemma 3. (triangle) If the center of a unit square u is contained in ABC, and each side of the triangle has length no more than 1, then u contains A, B, or C.

3. Lower bounds • Lemma 4. (rectangle) If the center of a unit square u is contained in the rectangle R=[0, 1]x[0, 0. 4], then u contains a vertex of R.

3. Lower bounds • Lemma 5. (trapezoid) If the unit square u has its center in [0, 1]2, u is completely above the xaxis, and u does not contain (0, 1) and (1, 1) then u covers the following: 1) the segment from (0. 2, 1) to (0. 8, 1) 2) some point (0, y) for 1/2≤y≤ 1 and some point (1, y) for 1/2≤y≤ 1. 3) either the point (0, √ 2 -1/2) or the point (1, √ 21/2).

3. Lower bounds To show s(n)≥k: • Find a set of n-1 “unavoidable” points in a square with side length k • Shrink this diagram by a factor of (1 -ε/k) to get a square with side length k-ε • Unit squares must contain one of these n 1 points in the interior, so we can pack at most n-1 squares • Therefore, s(n)>k-ε

3. Lower bounds s(2)=s(3)=2 • (1, 1) is unavoidable in [0, 2]2 by lemma 1 s(5)=2+1/√ 2 • P={ (1, 1), (1, 1+1/√ 2), (1+1/√ 2, 1+1/√ 2) } is unavoidable in [0, 2+1/√ 2]2 by lemma 1, 2, 3

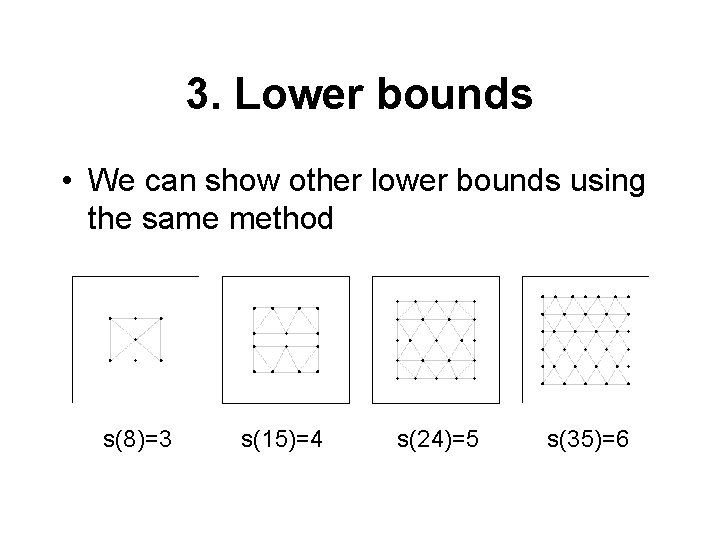
3. Lower bounds • We can show other lower bounds using the same method s(8)=3 s(15)=4 s(24)=5 s(35)=6

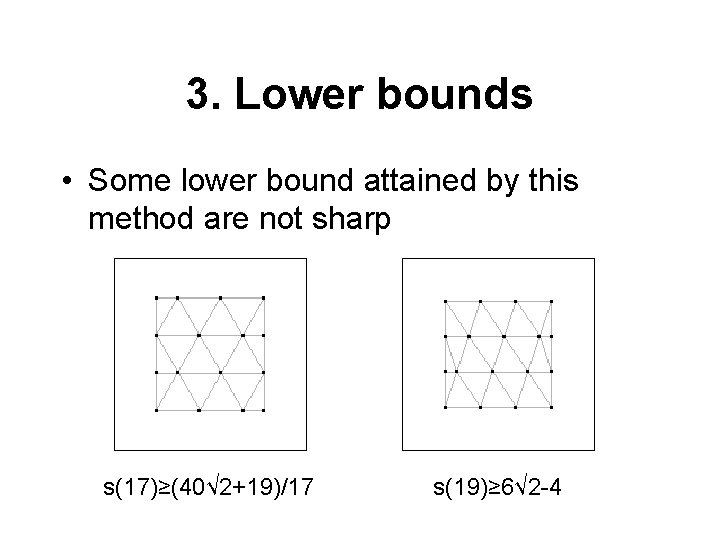
3. Lower bounds • Some lower bound attained by this method are not sharp s(17)≥(40√ 2+19)/17 s(19)≥ 6√ 2 -4

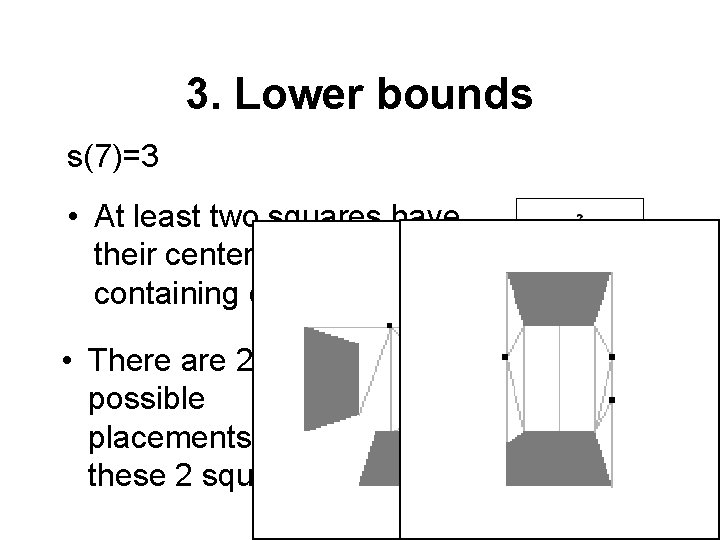
3. Lower bounds s(7)=3 • At least two squares have their centers in the regions containing question marks • There are 2 possible placements of these 2 squares

3. Lower bounds • s(n 2+ n/2 +1) ≥ 2√ 2 + 2(n-2)/√ 5 (Green, 2000) • s(n 2 -2)=s(n 2 -1)=n (Nagamochi, 2005) • Conjecture: If s(n 2 -k)=n, then s((n+1)2 k)=n+1

3. Lower Bounds

4. More problems • Packings of many shapes other than squares are studied

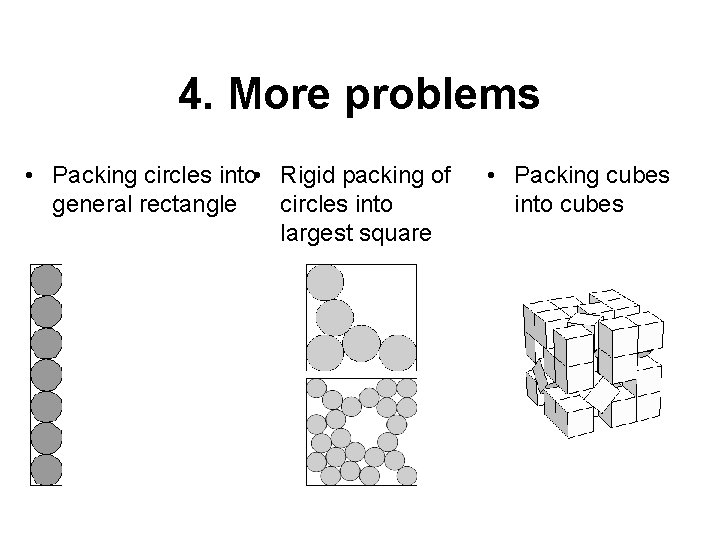
4. More problems • Packing circles into • Rigid packing of general rectangle circles into largest square • Packing cubes into cubes

References • http: //www. stetson. edu/~efriedma/paper s/squares. html - retrived Nov. 8, 2008 • http: //en. wikipedia. org/wiki/Packing_pro blem - retrived Nov. 8, 2008