WELCOME TO THE 4 TH ANNUAL DAMIEN HIGH













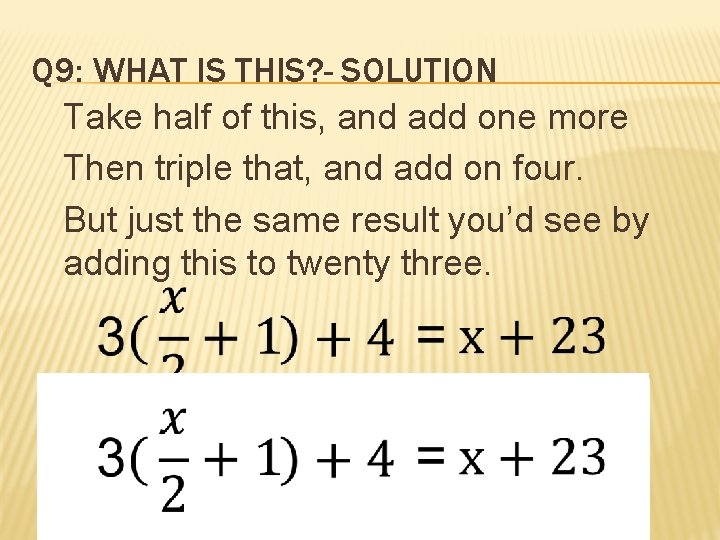







- Slides: 36

WELCOME TO THE 4 TH ANNUAL DAMIEN HIGH SCHOOL MATH COMPETITION 2013 If your school has not checked in, please send one student and one adult to the registration table at the front of the Activity Center.

SUPER QUIZ BOWL • This is a group competition in which many problems must be solved through collaboration. • Scratch paper is available at your tables, but the final answer for each problem must be written legibly in the box on the provided answer forms. • The final solution must be true for all the given clues. • Each question is worth different amounts of

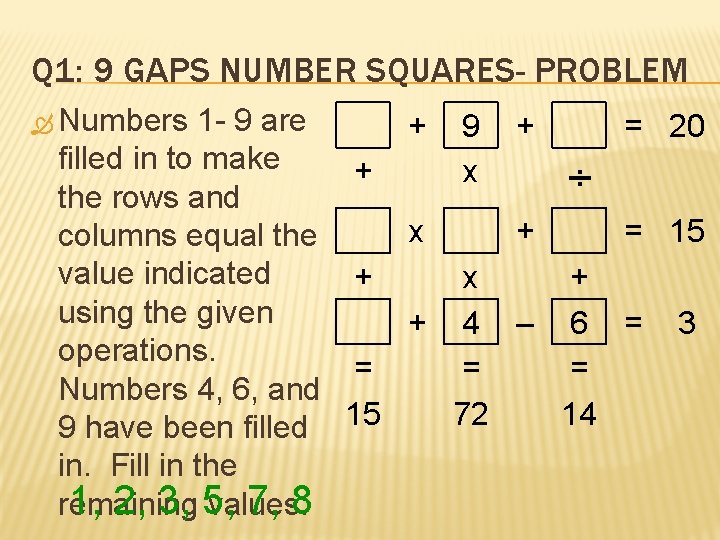
Q 1: 9 GAPS NUMBER SQUARES- PROBLEM Numbers 1 - 9 are filled in to make the rows and columns equal the value indicated using the given operations. Numbers 4, 6, and 9 have been filled in. Fill in the 1, 2, 3, 5, 7, 8 remaining values: + + x 9 x + = 20 ÷ + = 15 + x + + 4 – 6 = = 15 72 14 3

Q 1: 9 GAPS NUMBER SQUARES- SOLUTION 1 2 3 5 7 8 + + x 9 x + = 20 ÷ + = 15 + x + + 4 – 6 = = 15 72 14 3

Q 2: MID-POINT: PROBLEM

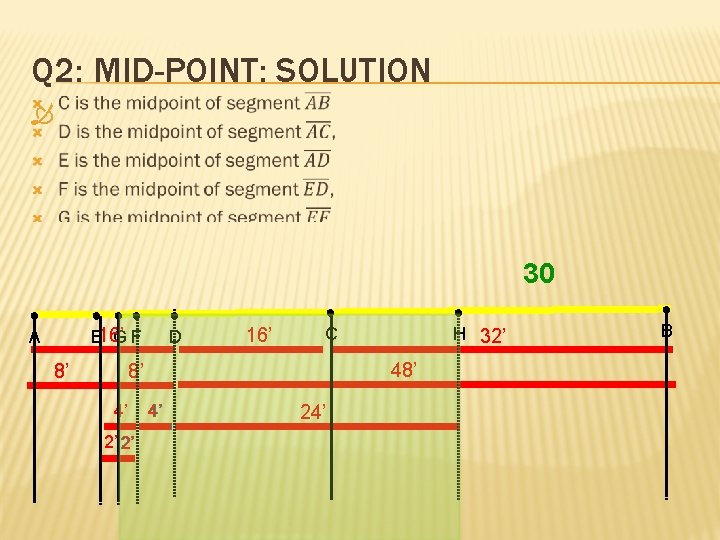
Q 2: MID-POINT: SOLUTION 30 ● A ● ●● E 16’ GF 8’ ● D 16’ ● C 48’ 8’ 4’ 2’ 2’ ● H 32’ 4’ 24’ ● B

Q 3: NUMBER MASTER MIND- INTRODUCTION I’m thinking of a 2 -digit number. The number does not begin with a 0 and none of the digits in the number are the same. (ex: 77 is not allowed). If you guess what my number is, I’ll tell you if any of the numbers in it are correct, and then I’ll tell you if any of them are in the correct place. Guess Number Places Correct Answer 62 31 75 47 17 Correct 0 1 1 1 2 0 0 0 1 2 We can play this game with any size number.

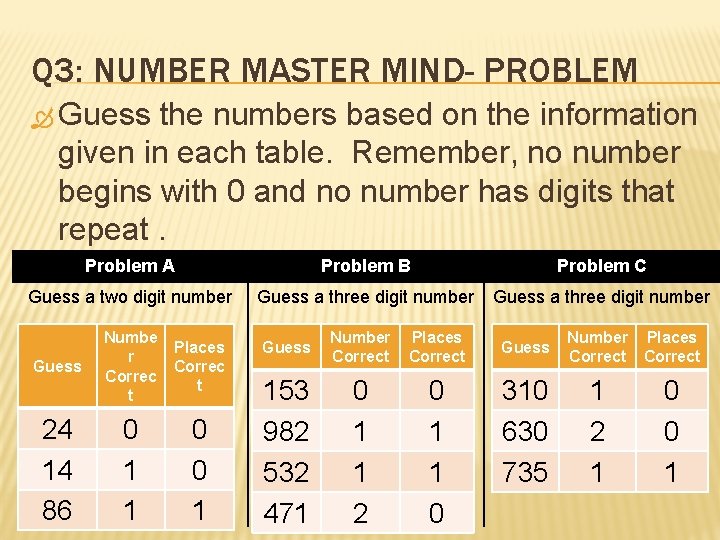
Q 3: NUMBER MASTER MIND- PROBLEM Guess the numbers based on the information given in each table. Remember, no number begins with 0 and no number has digits that repeat. Problem A Problem B Problem C Guess a two digit number Guess a three digit number Guess 24 14 86 Numbe Places r Correc t t 0 1 1 0 0 1 Guess Number Correct Places Correct 153 982 532 471 0 1 1 2 0 1 1 0 Guess 310 630 735 Number Places Correct 1 2 1 0 0 1

Q 3: NUMBER MASTER MIND- SOLUTIONS Each clue tells us something about our number Problem A Guess a two digit number Guess 24 14 86 Numbe Places r Correc t t 0 1 1 X 8 Y 1 0 0 1 Problem B Problem C Guess a three digit number Guess Number Correct Places Correct 153 982 532 471 0 1 1 2 0 1 1 0 A 7 B 4 C 2 Guess 310 630 735 Number Places Correct 1 2 1 0 0 1 If 6 & 0 _06 or 06_ If 6 & 3 _63 0 N 7 M L 6

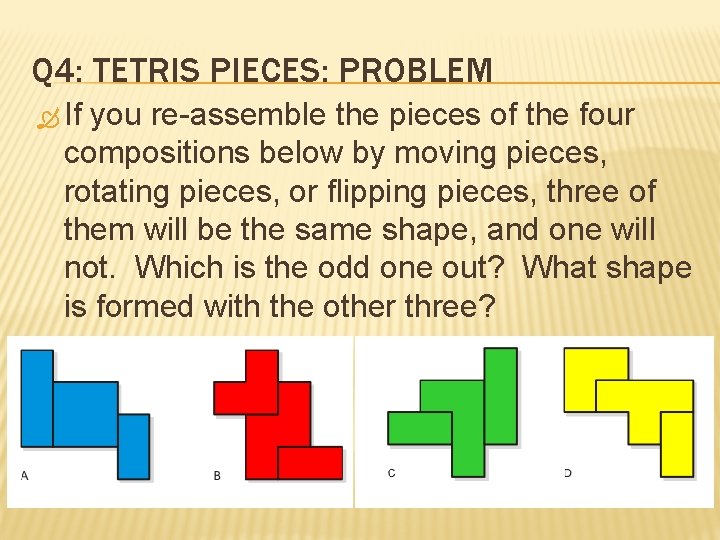
Q 4: TETRIS PIECES: PROBLEM If you re-assemble the pieces of the four compositions below by moving pieces, rotating pieces, or flipping pieces, three of them will be the same shape, and one will not. Which is the odd one out? What shape is formed with the other three?

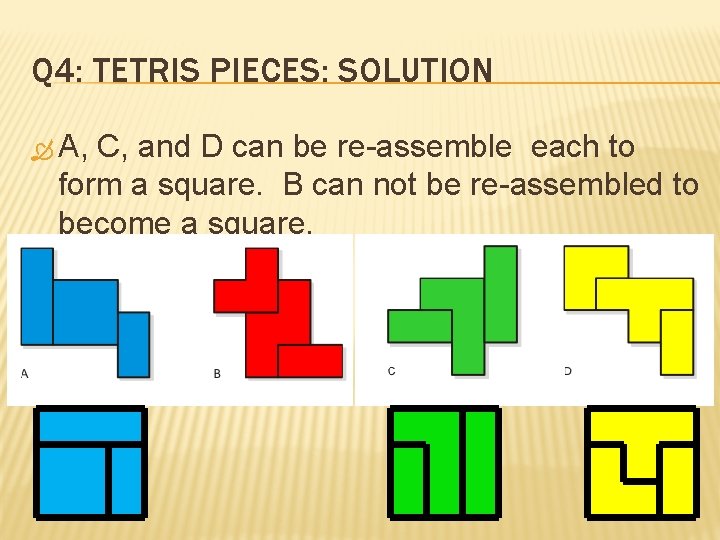
Q 4: TETRIS PIECES: SOLUTION A, C, and D can be re-assemble each to form a square. B can not be re-assembled to become a square.

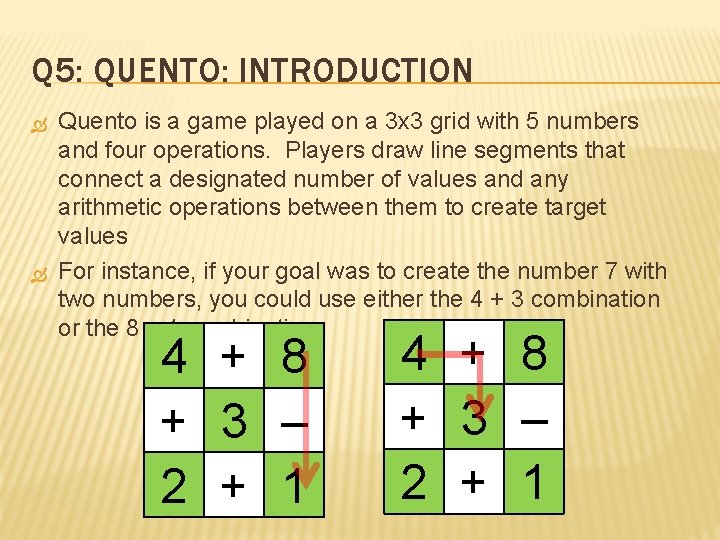
Q 5: QUENTO: INTRODUCTION Quento is a game played on a 3 x 3 grid with 5 numbers and four operations. Players draw line segments that connect a designated number of values and any arithmetic operations between them to create target values For instance, if your goal was to create the number 7 with two numbers, you could use either the 4 + 3 combination or the 8 – 1 combination 4 + 8 + 3 – 2 + 1

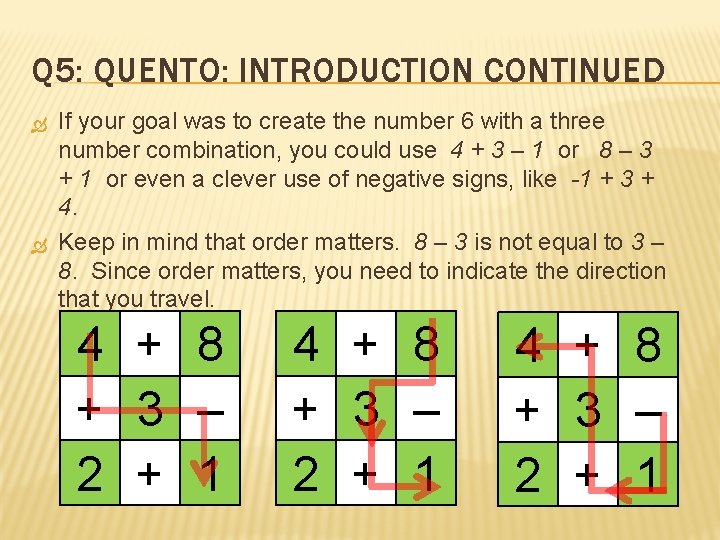
Q 5: QUENTO: INTRODUCTION CONTINUED If your goal was to create the number 6 with a three number combination, you could use 4 + 3 – 1 or 8 – 3 + 1 or even a clever use of negative signs, like -1 + 3 + 4. Keep in mind that order matters. 8 – 3 is not equal to 3 – 8. Since order matters, you need to indicate the direction that you travel. 4 + 8 + 3 – 2 + 1

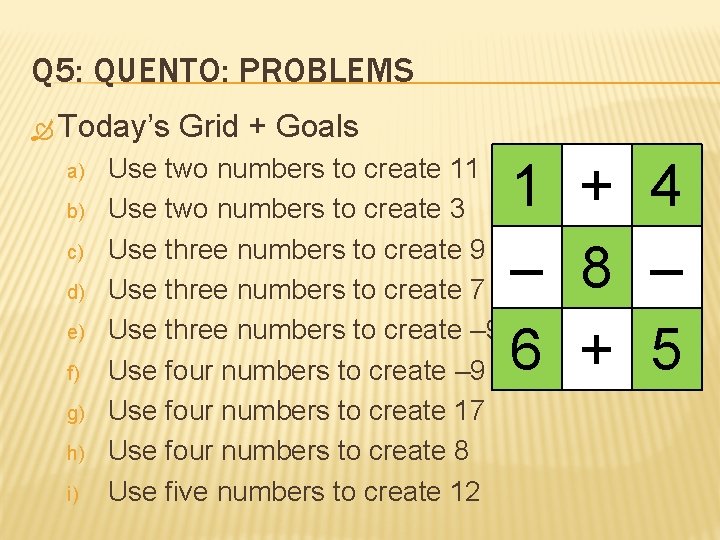
Q 5: QUENTO: PROBLEMS Today’s Grid + Goals a) b) c) d) e) f) g) h) i) Use two numbers to create 11 Use two numbers to create 3 Use three numbers to create 9 Use three numbers to create 7 Use three numbers to create – 9 Use four numbers to create – 9 Use four numbers to create 17 Use four numbers to create 8 Use five numbers to create 12 1 + 4 – 8 – 6 + 5

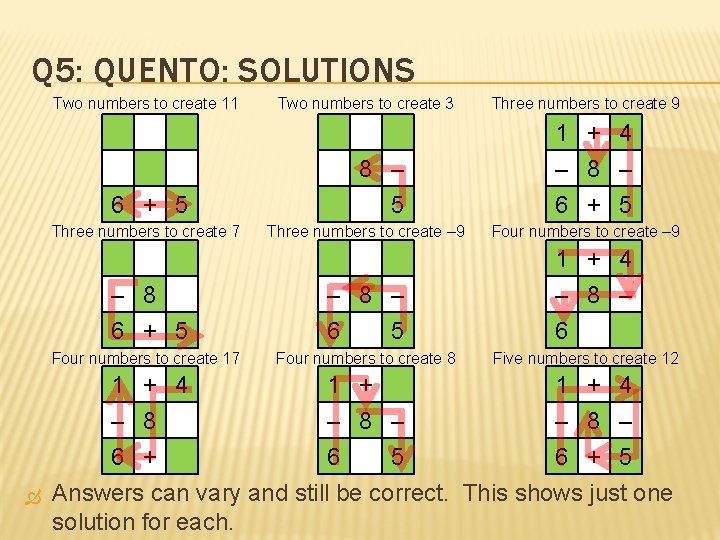
Q 5: QUENTO: SOLUTIONS Two numbers to create 11 6 + 5 Three numbers to create 7 Two numbers to create 3 8 – 5 Three numbers to create – 9 – 8 6 + 5 – 8 – 6 5 Four numbers to create 17 Four numbers to create 8 1 + 4 – 8 6 + 1 + – 8 – 6 5 Three numbers to create 9 1 + 4 – 8 – 6 + 5 Four numbers to create – 9 1 + 4 – 8 – 6 Five numbers to create 12 1 + 4 – 8 – 6 + 5 Answers can vary and still be correct. This shows just one solution for each.

Q 6: 6 NUMBERS: INTRODUCTION The game 6 NUMBERS allows players to use addition signs, subtraction signs, multiplication signs, division signs, (parentheses by grouping) and 6 numbers to write an expression equivalent to a target value. You do not need to use all the numbers, nor all the signs. Though you may repeat signs, but you may not use a number twice.

Q 6: 6 NUMBERS: INTRODUCTION CONTINUED Example: Create 106 from 2, 4, 3, 6, 10, and 100 Here are just some of the ways you can achieve your goal. You only need one. 100 + 6 = 106 100 + (2 x 3) = 106 (100 + 10) – (6 / 3) – (4 / 2) = 106

Q 6: 6 NUMBERS: PROBLEMS Goal 210 117 230 Numbers 1, 2, 4, 10, 25, 100 3, 4, 9, 10, 25, 50 1, 2, 8, 10, 75, 100 387 945 3, 4, 5, 12, 50, 100 1, 2, 8, 9, 50, 100 Using addition signs, subtraction signs, multiplication signs, division signs, parentheses, and only the 6 numbers given in each set, write an expression equivalent to each target value. Remember, you do not need to use all the numbers or all the signs. You can repeat signs, but you may

Q 6: 6 NUMBERS: SOLUTIONS This is just one solution. Others may be possible. Goal Numbers One Solution 210 1, 2, 4, 10, 25, 100 (100 x 2) + 10 117 3, 4, 9, 10, 25, 50 (10 + 3) x 9 230 1, 2, 8, 10, 75, 100 (75 x 2) + (10 x 8) (100+ 5 + (6 x 4)) x 387 3, 4, 5, 12, 50, 100 3 945 1, 2, 8, 9, 50, 100 (50+9) x (8 x 2) + 1

Q 7: MATH- DOKU: INTRODUCTION In variations of the popular puzzle game, Sudoku, each row and column in an n x n square has the numbers 1 to n listed only once in each row and column. For example, on a 3 x 3 grid, the numbers 1, 2, & 3 are listed once in each row and once in each column. For instance. 1 3 2 2 1 3 3 2 1

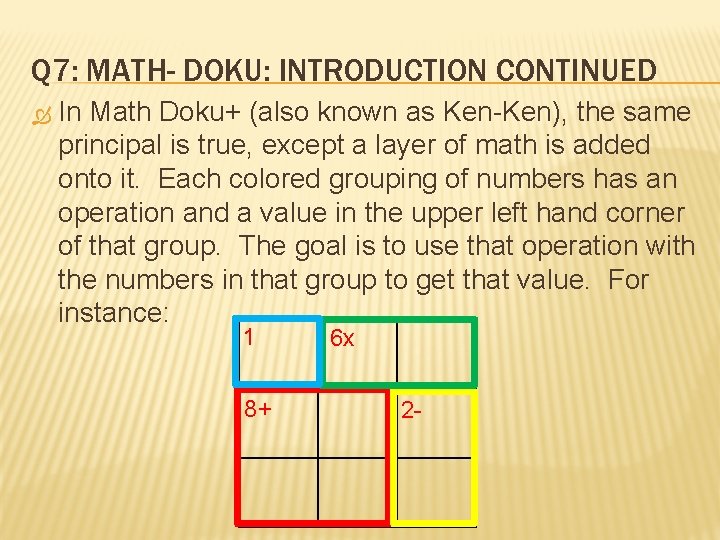
Q 7: MATH- DOKU: INTRODUCTION CONTINUED In Math Doku+ (also known as Ken-Ken), the same principal is true, except a layer of math is added onto it. Each colored grouping of numbers has an operation and a value in the upper left hand corner of that group. The goal is to use that operation with the numbers in that group to get that value. For instance: 1 8+ 6 x 2 -

Q 7: MATH- DOKU: INTRODUCTION CONTINUED The Sum (addition) of the numbers in the red grouping is 8 The difference (subtraction) of the two numbers in the yellow group is 2 (here there’s no need for a negative) The product (multiplication) of the numbers in the green group is 6 For this blue group, the number 1 goes inside. 1 1 8+ 6 x 3 2 1 3 2 2 2– 3 1 Remember, each row and column has the numbers 1, 2 and 3 with no repeats. This can be played on square grids as large as

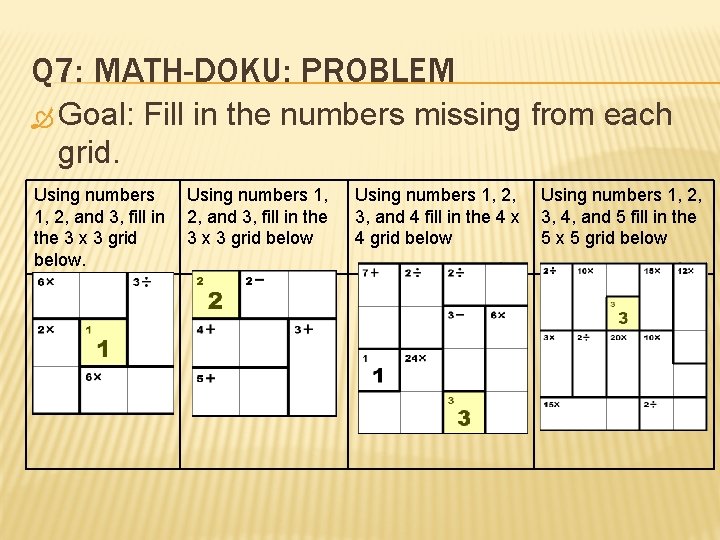
Q 7: MATH-DOKU: PROBLEM Goal: Fill in the numbers missing from each grid. Using numbers 1, 2, and 3, fill in the 3 x 3 grid below. Using numbers 1, 2, 3, and 4 fill in the 4 x 3, 4, and 5 fill in the 4 grid below 5 x 5 grid below

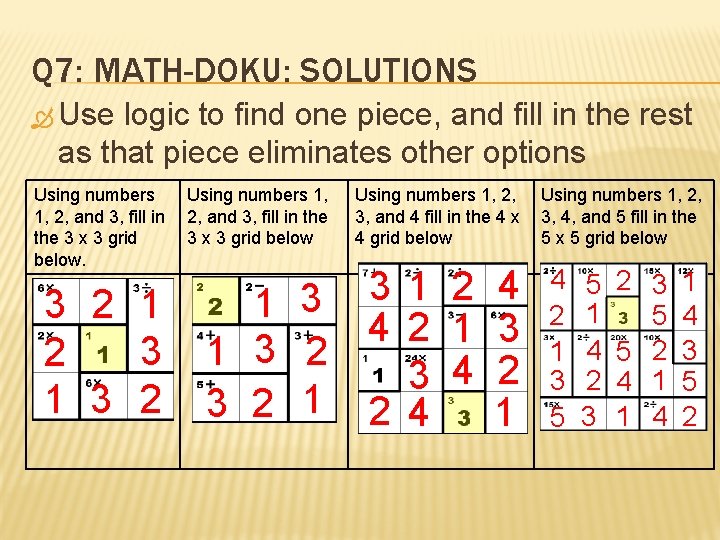
Q 7: MATH-DOKU: SOLUTIONS Use logic to find one piece, and fill in the rest as that piece eliminates other options Using numbers 1, 2, and 3, fill in the 3 x 3 grid below. 3 2 1 3 2 3 2 1 Using numbers 1, 2, 3, and 4 fill in the 4 x 3, 4, and 5 fill in the 4 grid below 5 x 5 grid below 3 1 2 4 2 1 3 4 2 4 4 3 2 1 4 2 1 3 5 5 1 4 2 3 5 5 2 4 1 1 4 3 5 2

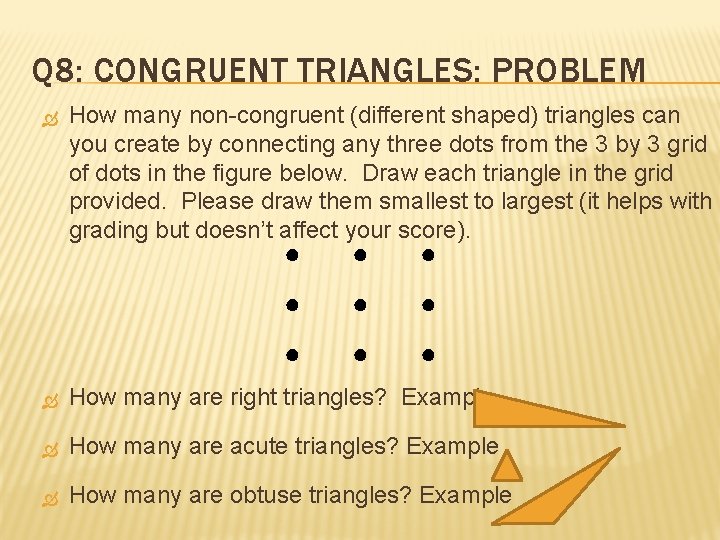
Q 8: CONGRUENT TRIANGLES: PROBLEM How many non-congruent (different shaped) triangles can you create by connecting any three dots from the 3 by 3 grid of dots in the figure below. Draw each triangle in the grid provided. Please draw them smallest to largest (it helps with grading but doesn’t affect your score). ● ● ● ● ● How many are right triangles? Example How many are acute triangles? Example How many are obtuse triangles? Example

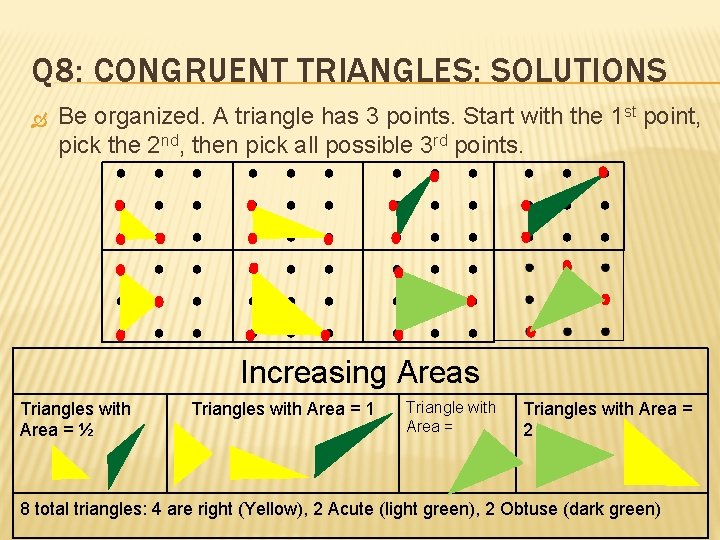
Q 8: CONGRUENT TRIANGLES: SOLUTIONS Be organized. A triangle has 3 points. Start with the 1 st point, pick the 2 nd, then pick all possible 3 rd points. ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● Increasing Areas Triangles with Area = ½ Triangles with Area = 1 Triangle with Area = Triangles with Area = 2 8 total triangles: 4 are right (Yellow), 2 Acute (light green), 2 Obtuse (dark green)

Q 9: WHAT IS THIS? - PROBLEM Another Classic Riddle: Take half of this, and add one more Then treble that, and add on four. But just the same result you’d see by adding this to twenty three. So what is this? You’ll have to say! Your fun with figures for today. Find what number represents This Hint: “Treble” means multiple by 3
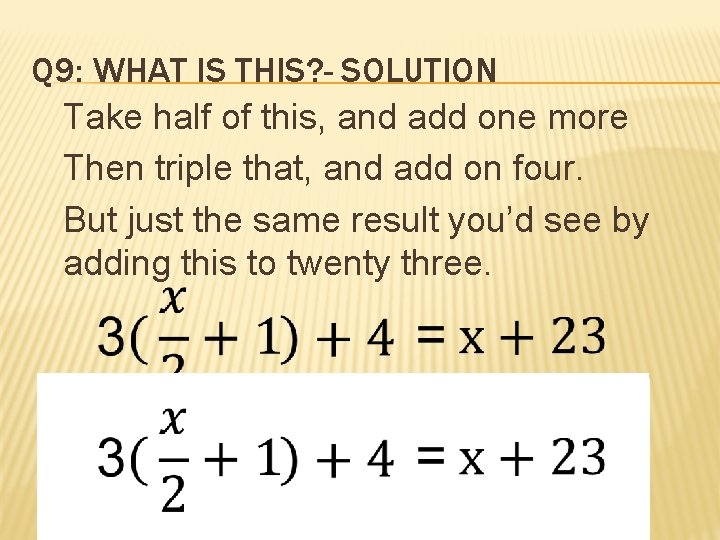
Q 9: WHAT IS THIS? - SOLUTION Take half of this, and add one more Then triple that, and add on four. But just the same result you’d see by adding this to twenty three.

Q 10: A CLOSE SECRET- PROBLEM A classic riddle “My age? ” She smiled. “You’ll have to guess. Just let me think. Ah that’s it yes. Reverse my age: divide by three: add thirty-four. My age you’ll see. ” That’s what she said. So can you say how old she must have been that day? Determine the woman’s age in the poem.

Q 10: A CLOSE SECRET- SOLUTION Her Age X 4 Y 2 2 X 4 “Reverse my age“Y (YX)/ “divide by three” 24/3 3 “add thirty-four” [(YX)/3] + 34 8 + 34 X 4 Y 2 “My age. ”

Q 11: NUMBER BROKEN INTO 4 PARTSPROBLEM The number 80 is the sum of four positive numbers a, b, c, d such that a increased by 4, b decreased by 4, c multiplied by 4, and d divided by 4 all equal the same number. Determine what this same number is (hint: it is a decimal) 2 Points for finding 2 consecutive positive integers that the number is trapped between. 2 Points for finding the number 3 Points for finding the values of a, b, c, and d.

Q 11: NUMBER BROKEN INTO 4 PARTSSOLUTION

Q 11: NUMBER BROKEN INTO 4 PARTSSOLUTION

CREDITS • • • Students Ambassadors AP Calculus Students Members of Math Department Parents, Teachers, and Principals Participants

SOURCES • Many of these problems, as past problems from math Competitions, were inspired by apps from smart phones. If you’re going play on your phone, play smart! Nine. Gaps 6 Numbers Math Doku+ Quento

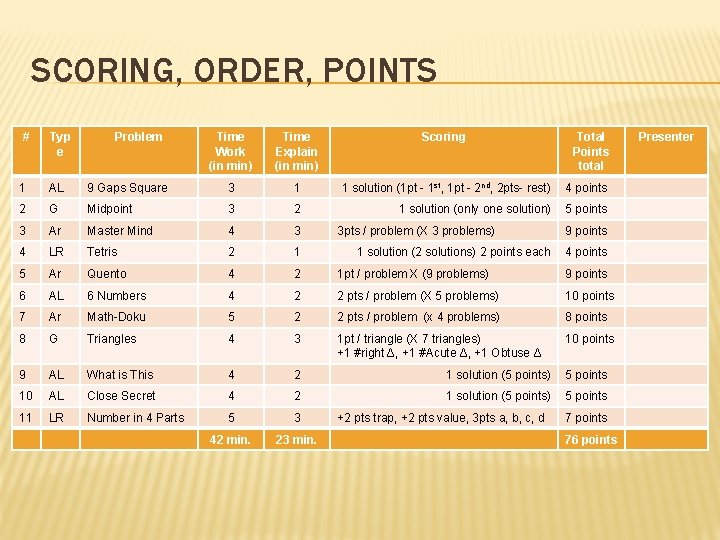
SCORING, ORDER, POINTS # Typ e Problem Time Work (in min) Time Explain (in min) Scoring Total Points total 1 AL 9 Gaps Square 3 1 1 solution (1 pt - 1 st, 1 pt - 2 nd, 2 pts- rest) 4 points 2 G Midpoint 3 2 1 solution (only one solution) 3 Ar Master Mind 4 3 4 LR Tetris 2 1 5 Ar Quento 4 2 1 pt / problem X (9 problems) 9 points 6 AL 6 Numbers 4 2 2 pts / problem (X 5 problems) 10 points 7 Ar Math-Doku 5 2 2 pts / problem (x 4 problems) 8 points 8 G Triangles 4 3 1 pt / triangle (X 7 triangles) +1 #right Δ, +1 #Acute Δ, +1 Obtuse Δ 10 points 9 AL What is This 4 2 1 solution (5 points) 5 points 10 AL Close Secret 4 2 1 solution (5 points) 11 LR Number in 4 Parts 5 3 42 min. 23 min. 3 pts / problem (X 3 problems) 1 solution (2 solutions) 2 points each +2 pts trap, +2 pts value, 3 pts a, b, c, d 5 points 9 points 4 points 5 points 76 points Presenter
 Damien ah yen
Damien ah yen Dr damien ringuenet
Dr damien ringuenet Pauquet diététicien
Pauquet diététicien Damien givry
Damien givry Damien darcy
Damien darcy Damien ettere
Damien ettere Damien neven
Damien neven Away from the flock damien hirst
Away from the flock damien hirst Away from the flock damien hirst
Away from the flock damien hirst Damien jolley
Damien jolley Lhc location
Lhc location Damien
Damien Marie louise damien
Marie louise damien Pauquet
Pauquet O que é um ponto na linguagem visual
O que é um ponto na linguagem visual Damien coleman
Damien coleman Damien kiernan
Damien kiernan Damien contandriopoulos
Damien contandriopoulos Damien charles weber
Damien charles weber Damien dupré
Damien dupré 4 squares = 5 9 squares =
4 squares = 5 9 squares = Ls agenda
Ls agenda Damien devaux
Damien devaux Damien stanley
Damien stanley Wise men three clever are we
Wise men three clever are we Welcome to super hero high
Welcome to super hero high Welcome to your senior year of high school
Welcome to your senior year of high school Welcome to hillcrest high
Welcome to hillcrest high Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Slidetodoc
Slidetodoc Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Tư thế worm breton là gì
Tư thế worm breton là gì Chúa yêu trần thế
Chúa yêu trần thế Kể tên các môn thể thao
Kể tên các môn thể thao Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất