Vector Functions and Space Curves Vector Functions and

Vector Functions and Space Curves

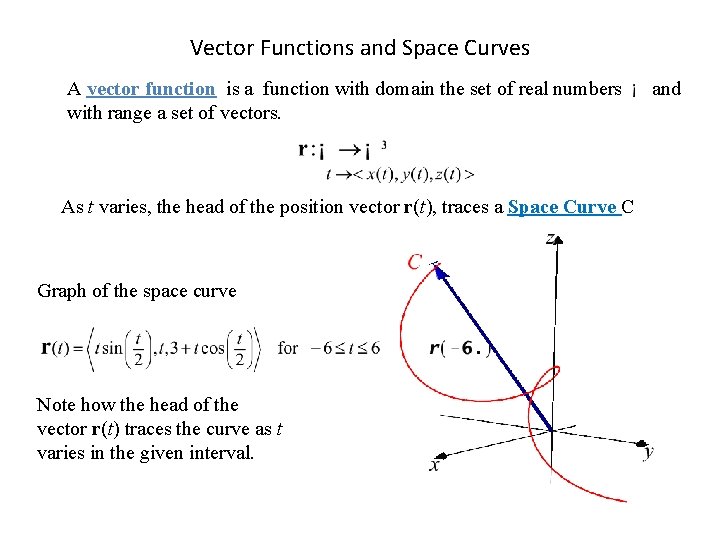
Vector Functions and Space Curves A vector function is a function with domain the set of real numbers with range a set of vectors. As t varies, the head of the position vector r(t), traces a Space Curve C Graph of the space curve Note how the head of the vector r(t) traces the curve as t varies in the given interval. and

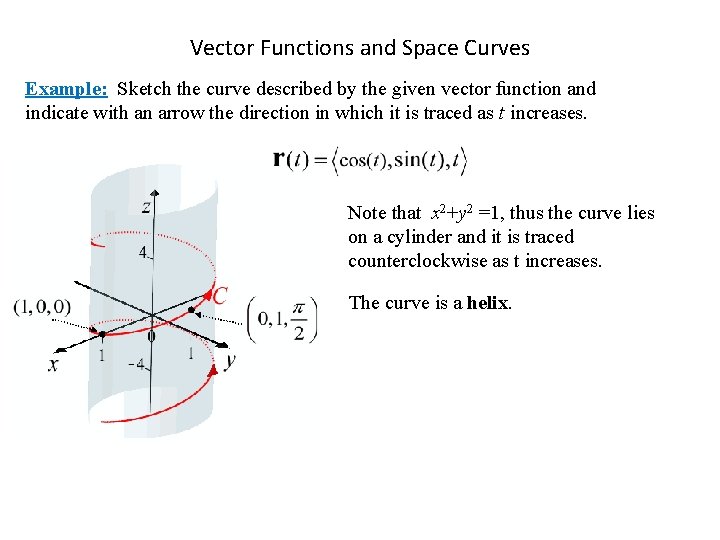
Vector Functions and Space Curves Example: Sketch the curve described by the given vector function and indicate with an arrow the direction in which it is traced as t increases. Note that x 2+y 2 =1, thus the curve lies on a cylinder and it is traced counterclockwise as t increases. The curve is a helix.

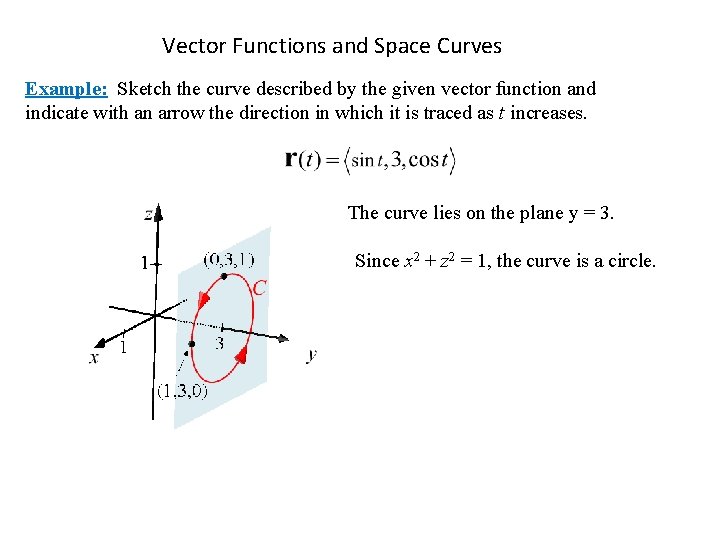
Vector Functions and Space Curves Example: Sketch the curve described by the given vector function and indicate with an arrow the direction in which it is traced as t increases. The curve lies on the plane y = 3. Since x 2 + z 2 = 1, the curve is a circle.

Vector Functions and Space Curves The domain of a vector function r(t) consists of all values of t for which r(t) is defined. Example: Find the domain of is defined for all t is defined for t ≥ 1 is defined for t ≤ 5 Domain of r(t) = {t | 1 ≤ t ≤ 5} The Limit of a vector function r(t) is the limit of its function components. Provided each limit exists. Example:

Vector Functions and Space Curves A curve can be represented also by the intersection of two surfaces. For instance, a line is the intersection of two planes. Given the surfaces F(x, y, z) = 0 G(x, y, z) = 0 To find parametric equations of the curve of intersection: Choose one of x, y or z as a function of t and solve F(x, y, z) = 0, G(x, y, z) = 0 for the remaining variables.

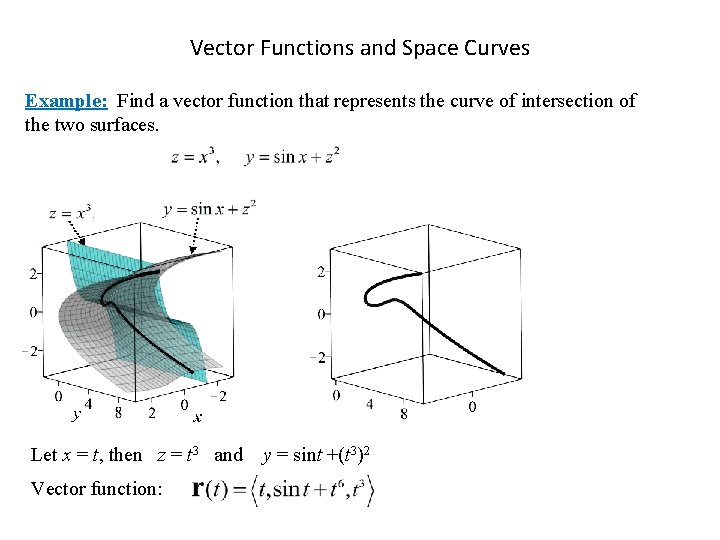
Vector Functions and Space Curves Example: Find a vector function that represents the curve of intersection of the two surfaces. Let x = t, then z = t 3 and Vector function: y = sint +(t 3)2

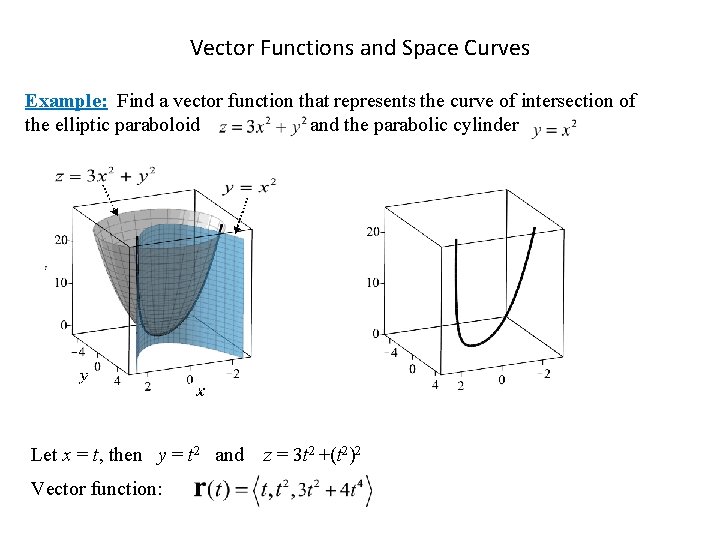
Vector Functions and Space Curves Example: Find a vector function that represents the curve of intersection of the elliptic paraboloid and the parabolic cylinder Let x = t, then y = t 2 and Vector function: z = 3 t 2 +(t 2)2

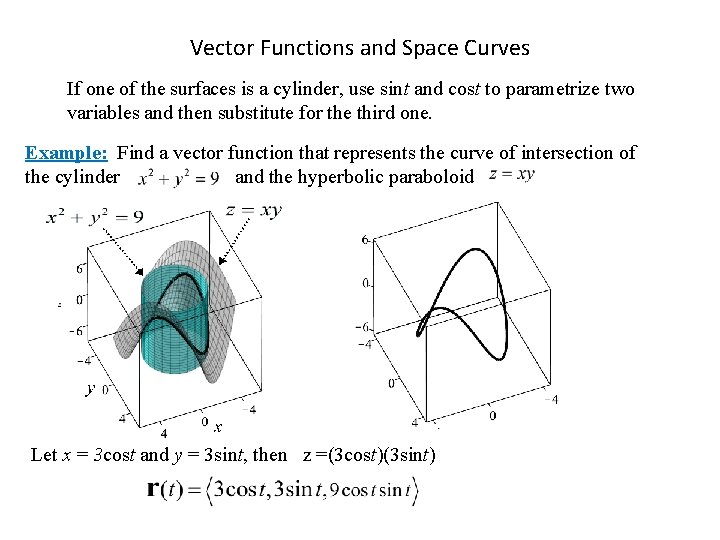
Vector Functions and Space Curves If one of the surfaces is a cylinder, use sint and cost to parametrize two variables and then substitute for the third one. Example: Find a vector function that represents the curve of intersection of the cylinder and the hyperbolic paraboloid Let x = 3 cost and y = 3 sint, then z =(3 cost)(3 sint)

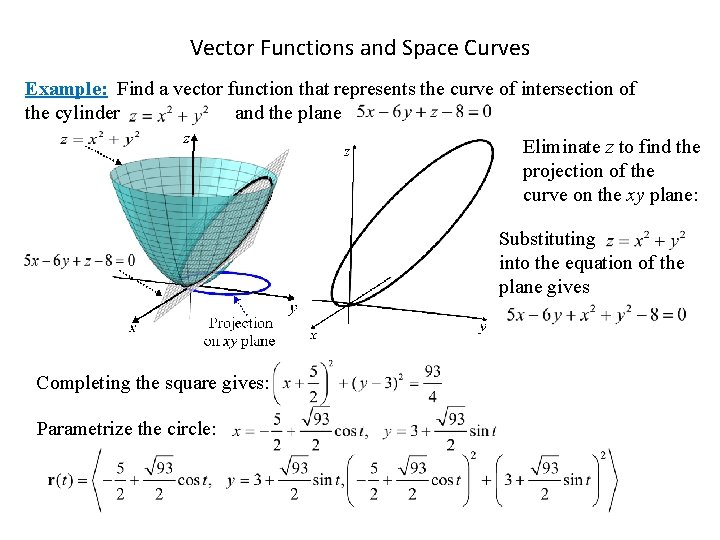
Vector Functions and Space Curves Example: Find a vector function that represents the curve of intersection of the cylinder and the plane Eliminate z to find the projection of the curve on the xy plane: Substituting into the equation of the plane gives Completing the square gives: Parametrize the circle:

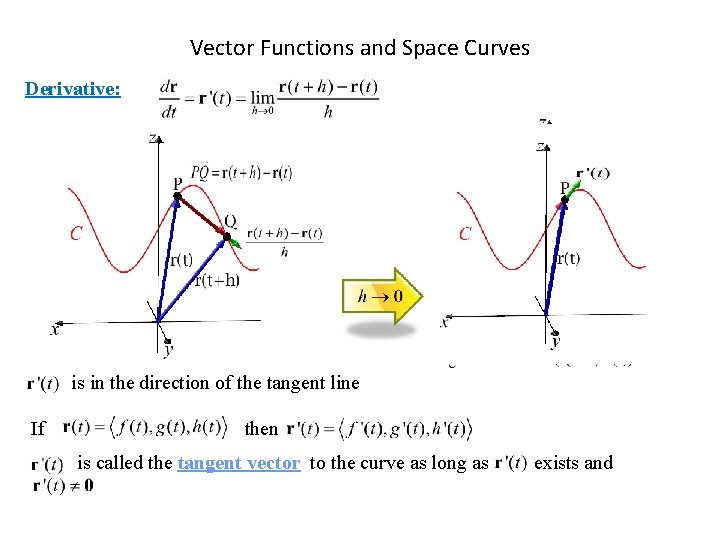
Vector Functions and Space Curves Derivative: is in the direction of the tangent line If then is called the tangent vector to the curve as long as exists and

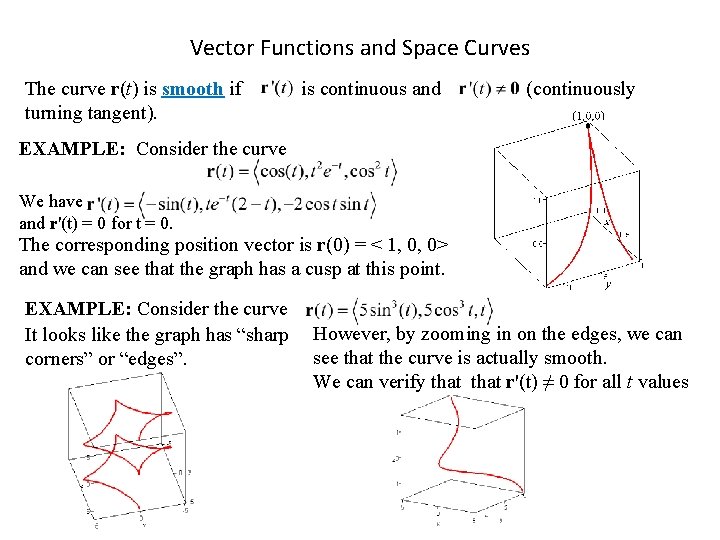
Vector Functions and Space Curves The curve r(t) is smooth if turning tangent). is continuous and (continuously EXAMPLE: Consider the curve We have and r'(t) = 0 for t = 0. The corresponding position vector is r(0) = < 1, 0, 0> and we can see that the graph has a cusp at this point. EXAMPLE: Consider the curve It looks like the graph has “sharp corners” or “edges”. However, by zooming in on the edges, we can see that the curve is actually smooth. We can verify that r'(t) ≠ 0 for all t values

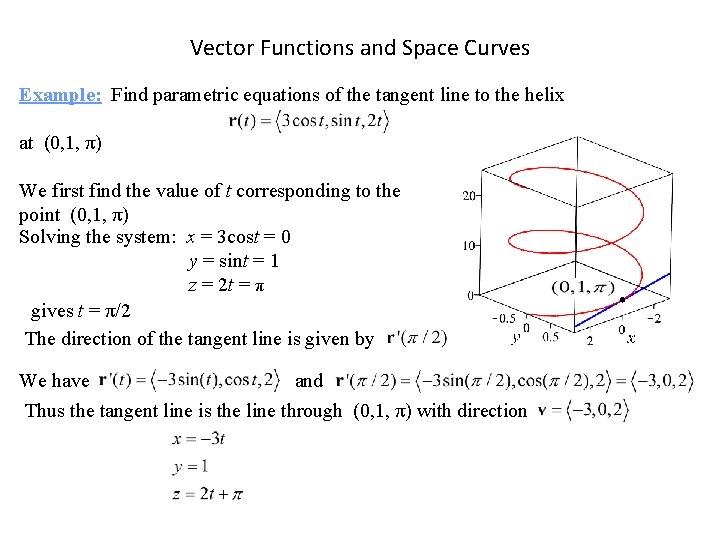
Vector Functions and Space Curves Example: Find parametric equations of the tangent line to the helix at (0, 1, π) We first find the value of t corresponding to the point (0, 1, π) Solving the system: x = 3 cost = 0 y = sint = 1 z = 2 t = π gives t = π/2 The direction of the tangent line is given by We have and Thus the tangent line is the line through (0, 1, π) with direction

Vector Functions and Space Curves The Unit Tangent Vector is the unit vector in the direction of Example: Find the unit tangent vector to the curve at t = 1.