In detail this means three conditions 1 f

In detail this means three conditions: 1. f has to be defined at c. 2. the limit on the left hand side of that equation has to exist. 3. the value of this limit must equal f(c).

Definition in terms of limits of sequences One can instead require that for any sequence of points in the domain which converges to c. the corresponding sequence converges to f(c). In mathematical notation

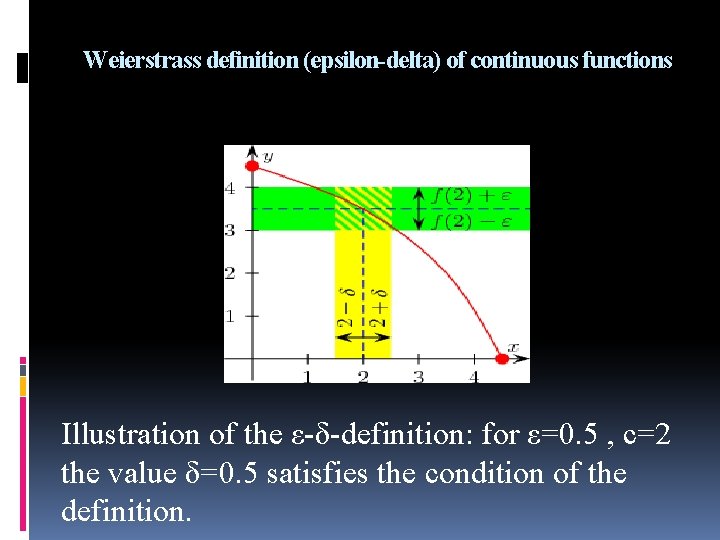
Weierstrass definition (epsilon-delta) of continuous functions Illustration of the ε-δ-definition: for ε=0. 5 , c=2 the value δ=0. 5 satisfies the condition of the definition.

Given a function f as above and an element c of the domain I, f is said to be continuous at the point c if the following holds: For any number ε > 0, however small, there exists some number δ > 0 such that for all x in the domain of f with c − δ < x < c + δ, the value of f(x) satisfies

Alternatively written, continuity of f : I → R at c ∈ I means that for every ε > 0 there exists a δ > 0 such that for all x ∈ I: ,

The following functions are continuous everywhere üPolynomials üRational functions üTrigonometric functions üInverse trigonometric functions üExponential and log functions üPower functions

A right-continuous function Directional and semi-continuity A right-continuous function A left-continuous function

f is said to be right-continuous at the point c if the following holds: For any number ε > 0 however small, there exists some number δ > 0 such that for all x in the domain with c < x < c + δ, the value of f(x) will satisfy

This is the same condition as for continuous functions, except that it is required to hold for x strictly larger than c only. Requiring it instead for all x with c − δ < x < c yields the notion of left-continuous functions. A function is continuous if and only if it is both rightcontinuous and left-continuous.

Definition : Let f be a function with domain D < R and let a be an element of D. We will say that f is continuous at a if, for each ϵ > 0, there is a > 0 , such that whenever xЄ D and

Example : Prove that f(x) = x^2 is continuous at x = 2. Solution: We have If we insist that , then 1 < x < 3 and so . Thus, given ϵ > 0, if we choose, then

Whenever This proves that f is continuous at 2.

uniformly continuous Example uniformly continuous

Uniform continuity Definition for functions on metric spaces Given metric spaces (X, d 1) and (Y, d 2), a function f : X → Y is called uniformly continuous if for every real number ε > 0 there exists δ > 0 such that for every x, y ∈ X with d 1(x, y) < δ, we have that d 2(f(x), f(y)) < ε. If X and Y are subsets of the real numbers, d 1 and d 2 can be the standard Euclidean norm, || · ||, yielding the definition: for all ε > 0 there exists a δ > 0 such that for all x, y ∈ X, |x − y| < δ implies |f(x) − f(y)| < ε. The difference between being uniformly continuous, and simply being continuous at every point, is that in uniform continuity the value of δ depends only on ε and not on the point in the domain

Discontinuity of the first and second

One-sided Lipschitz Let F(x) be an upper semi-continuous function of x, and that F(x) is a closed, convex set for all x. Then F is one-sided Lipschitz. if for some C for all x 1 and x 2

Pointwise Holder continuity

Lipschitz continuity The function f(x) = √x² + 5 defined for all real numbers is Lipschitz continuous with the Lipschitz constant K =1

Uniform and Local holder continuity:

Holder Continuous / Holder Continuity Example: F(x)=√x defined on [0, 1] is Holder continuous for α ≤ 1/2.

Lipschitz Condition and continuous

Lipschitz Functions Definition: Let f (x) be defined on an interval I and suppose we can find two positive constants M and a such t hat Then f is said to satisfy a Lipschitz Condition o f order a and we say that f ∈ Lip (a ). Example : Take f (x) = x on the interval [a, b ]. Then That implies that f ∈ Lip (1). Now take f (x) = x on the interval [a, b ]. Then

with M = 2 max(|a|, |b |). Hence, again f ∈ Lip (1). The function f (x) = 1 /x on (0, 1). Is it Lip (1) ? How about Lip (1/2)? How about Lip (a )? Lipschitz and Continuity Theorem: If f ∈ Lip (a ) on I, then f is continuous; indeed, uniformly continuous o n I. Last time we did continuity with ε and δ An altrnative definition of continuity familar from calculus is: f is continuous at x = c if:

q. If 0 < α ≤ β ≤ 1 then all Hölder continuous functions on a bounded set Ω are also Hölder continuous. This also includes β = 1 and therefore all lipschitz continuous functions on a bounded set are also C 0, α Hölder continuous. q. The function defined on [0, 1] is not Lipschitz continuous, but is C 0, α Hölder continuous for α≥ ½ q. In the same manner, the function f (x) = xβ (with β ≤ 1) defined on [0, 1] serves as a prototypical example of a function that is C 0, α Hölder continuous for 0 < α ≤ β, but not for α > β. q. There are examples of uniformly continuous functions that are not α– Hölder continuous for any α. For instance, the function defined on [0, 1/2] by f(0) = 0 and by f(x) = 1 / log(x) otherwise is continuous, and therefore uniformly continuous by the. Heine-Cantor theorem. It does not satisfy a Hölder condition of any order, however. q. For α > 1, any α–Hölder continuous function on [0, 1] is a constant.

absolutely continuous Definition Let I be an interval in the real line R. A function f: I → R is absolutely continuous on I if for every positive number ε, there is a positive number δ. then such that whenever a finite sequence of pair wise disjoint subintervals (xk, yk) of I satisfies

Equivalent definitions for all x on [a, b. [ If these equivalent conditions are satisfied then necessarily g = f ′ almost everywhere. The following conditions on a real-valued function f on a compact interval [a, b] are equivalent: (1) f is absolutely continuous; (2) f has a derivative f ′ almost everywhere , the derivative is Lebesgue integrable, and for all x on[a, b] ; (3) there exists a Lebesgue integrable function g on [a, b] such that for all x on [a, b]

Every absolutely continuous function is uniformly continuous and, therefore, continuous Every lipschitz - continuous function is absolutely continuous

Examples The following functions are continuous everywhere but not absolutely continuous: • the cantor function ; • the function on a finite interval containing the origin;

Generalizations Let (X, d) be a metric space and let I be an interval in the real line R. A function f: I → X is absolutely continuous on I if for every positive number ε , there is a positive number δ such that whenever a finite sequence of pairwise disjointsub-intervals [xk, yk] of I satisfies

Absolute continuity of measures A measure μ on Borel subsets of the real line is absolutely continuous with respect to Lebesgue measure λ (in other words, dominated by λ) if μ(A) = 0 for every set A for which λ(A) = 0. This is written as “μ << λ. ” In most applications, if a measure on the real line is simply said to be absolutely continuous — without specifying with respect to which other measure it is absolutely continuous — then absolute continuity with respect to Lebesgue measure is meant. The same holds for Rn for all n=1, 2, 3,

Let X and Y be metric space, and let f be a function from X to Y. Then f is Cauchy-continuous if and only if, given any Cauchy sequence (x 1, x 2, …) in X, the sequence (f(x 1), f(x 2), …) is a Cauchy sequence in Y.

equicontinuous Let X and Y be two metric space, and F a family of functions from X to Y. The family F is equicontinuous at a point x 0 ∈ X if for every ε > 0, there exists a δ > 0 such that d (ƒ(x 0), ƒ(x)) < ε for all ƒ ∈ F and all x such that d(x 0, x) < δ. The family is equicontinuous if it is equicontinuous at each point of X. The family F is uniformly equicontinuous if for every ε > 0, there exists a δ > 0 such that d(ƒ(x 1), ƒ(x 2)) < ε for all ƒ ∈ F and all x 1, x 2 ∈ X such that d(x 1, x 2) < δ. [ For comparison, the statement 'all functions ƒ in F are continuous' means that for every ε > 0, every ƒ ∈ F, and every x 0 ∈ X, there exists a δ > 0 such that d(ƒ(x 0), ƒ(x)) < ε for all x ∈ X such that d(x 0, x) < δ. For continuity, δ may depend on ε, x 0 and ƒ. For uniform continuity, δ may depend on ε, and ƒ. For equicontinuity, δ may depend on ε, and x 0. For uniform equicontinuity, δ may solely depend on ε.

Every Lipschitz continuous map between two metric spaces is uniformly continuous. In particular, every function which is differentiable and has bounded derivative is uniformly continuous. More generally, every Holder continuous function is uniformly continuous. Every member of a uniformly equi continuous set of functions is uniformly continuous. The tangent function is continuous on the interval (−π/2, π/2) but is not uniformly continuous on that interval. exponential function x → ex is continuous everywhere The on the real line but is not uniformly continuous on the line.

Uniformly Continuous continuous

If f is continuous on [a, b], then f is uniformly continuous on [a, b]. If f is a Continuous functions of a compact set , it is uniformly Continuous on that set.

uniformly continuous and not lipschitz continuous Converse Example F(x)=√x on [0, 1] Every lipschitz continuous map is uniformly continuous

uniformly continuous functions that are not α– Holder continuous There are examples of uniformly continuous functions that are not α–Holder continuous for any α. For instance, the function defined on [0, 1/2] by f (0) = 0 and by f(x) = 1 / log(x) otherwise is continuous, and therefore uniformly continuous by the Heine-Cantor theorem. It does not satisfy a Holder condition of any order. Any Holder continuous function is uniformly continuous

Absolute continuity implies uniform continuity For a uniformly continuous function f defined on an interval of the real line, if it is piecewise convex, then it is also absolutely continuous.

Every uniformly continuous function is also Cauchy-continuous uniformly continuous function For example, define a two-valued function so that f(x) is 0 when x 2 is less than 2 but 1 when x 2 is greater than 2. (Note that x 2 is never equal to 2 for any rational number x. ) This function is continuous on ℚ but not Cauchy-continuous, since it can't be extended to ℝ. On the other hand, any uniformly continuous function on ℚ must be Cauchy-continuous. For a non-uniform example on ℚ, let f(x) be 2 x; this is not uniformly continuous (on all of ℚ), but it is Cauchy-continuous.

Lipschitz and holder continuous Let f satisfies |f(x+u)−f(x)|≤L|u|^ α for some constants L and α. If α=1 then f is called Lipschitz continuous, and if 0<α<1 then f is Hölder continuous

A generalization of Lipschitz continuity is called holder continuity If f is Lipschitz continuity , then f is absolutely Every member of a uniformly equicontinuous set of function s is uniformly continuous A set of functions with the same lipschitz constant is (uniformly) equicontinuous.

For linear transformations f: V→W, uniform continuity is equivalent to continuity.