COMP 482 Design and Analysis of Algorithms Spring

COMP 482: Design and Analysis of Algorithms Spring 2012 Lecture 16 Prof. Swarat Chaudhuri

6. 3 Segmented Least Squares

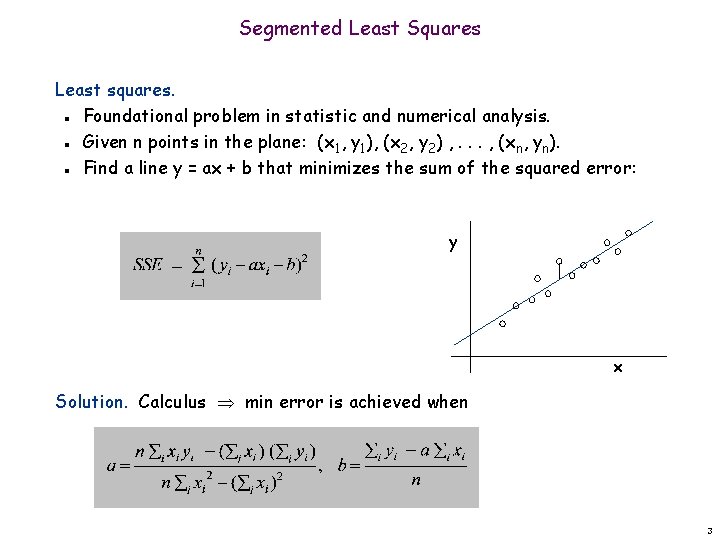
Segmented Least Squares Least squares. Foundational problem in statistic and numerical analysis. Given n points in the plane: (x 1, y 1), (x 2, y 2) , . . . , (xn, yn). Find a line y = ax + b that minimizes the sum of the squared error: n n n y x Solution. Calculus min error is achieved when 3

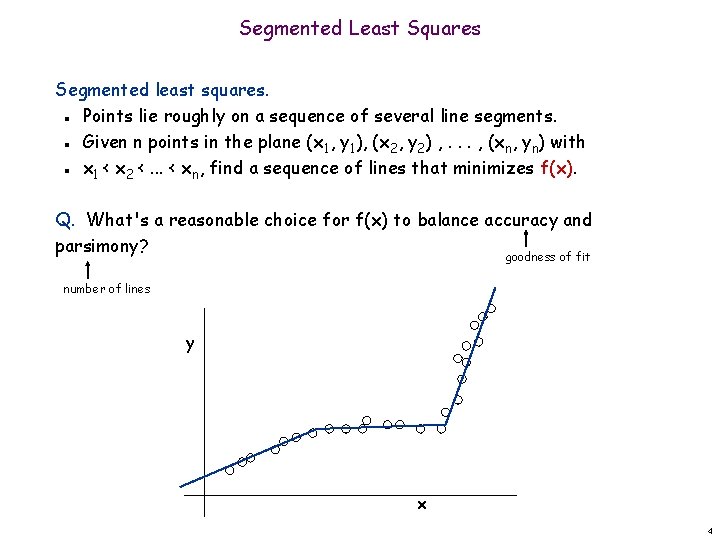
Segmented Least Squares Segmented least squares. Points lie roughly on a sequence of several line segments. Given n points in the plane (x 1, y 1), (x 2, y 2) , . . . , (xn, yn) with x 1 < x 2 <. . . < xn, find a sequence of lines that minimizes f(x). n n n Q. What's a reasonable choice for f(x) to balance accuracy and parsimony? goodness of fit number of lines y x 4

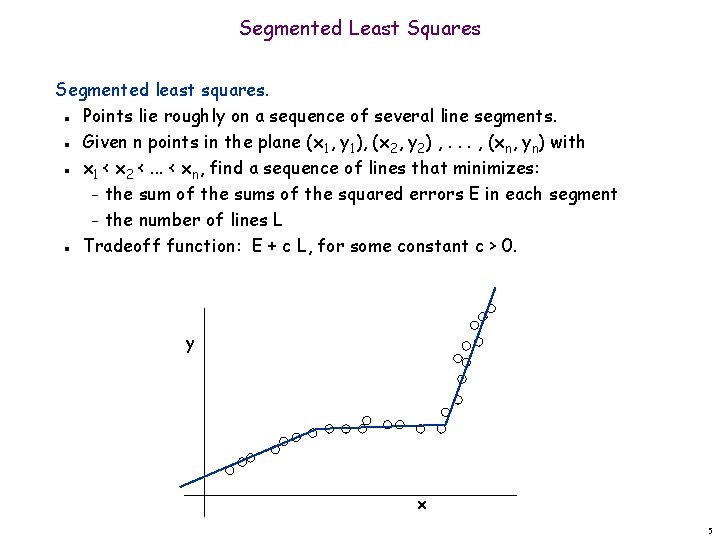
Segmented Least Squares Segmented least squares. Points lie roughly on a sequence of several line segments. Given n points in the plane (x 1, y 1), (x 2, y 2) , . . . , (xn, yn) with x 1 < x 2 <. . . < xn, find a sequence of lines that minimizes: – the sum of the sums of the squared errors E in each segment – the number of lines L Tradeoff function: E + c L, for some constant c > 0. n n y x 5

Dynamic Programming: Multiway Choice Notation. OPT(j) = minimum cost for points p 1, pi+1 , . . . , pj. e(i, j) = minimum sum of squares for points pi, pi+1 , . . . , pj. n n To compute OPT(j): Last segment uses points pi, pi+1 , . . . , pj for some i. Cost = e(i, j) + c + OPT(i-1). n n 6

Segmented Least Squares: Algorithm INPUT: n, p 1, …, p. N , c Segmented-Least-Squares() { M[0] = 0 for j = 1 to n for i = 1 to j compute the least square error eij for the segment pi, …, pj for j = 1 to n M[j] = min 1 i j (eij + c + M[i-1]) return M[n] } O(n 3). can be improved to O(n 2) by pre-computing various statistics Running time. Bottleneck = computing e(i, j) for O(n 2) pairs, O(n) per pair using previous formula. n 7

6. 6 Sequence Alignment

String Similarity How similar are two strings? n ocurrance n occurrence o c u r r o c c u r a n c e - r e n c e 5 mismatches, 1 gap o c - u r o c c u r r a n c e r e n c e 1 mismatch, 1 gap o c - u r o c c u r r - r e a n c e - n c e 0 mismatches, 3 gaps 9

Edit Distance Applications. Basis for Unix diff. Speech recognition. Computational biology. n n n Edit distance. [Levenshtein 1966, Needleman-Wunsch 1970] Gap penalty ; mismatch penalty pq. Cost = sum of gap and mismatch penalties. n n C T G A C C T - C T G A C C T G A C T A C A T C C T G A C - T A C A T TC + GT + AG+ 2 CA 2 + CA 10

Sequence Alignment Goal: Given two strings X = x 1 x 2. . . xm and Y = y 1 y 2. . . yn find alignment of minimum cost. Def. An alignment M is a set of ordered pairs xi-yj such that each item occurs in at most one pair and no crossings. Def. The pair xi-yj and xi'-yj' cross if i < i', but j > j'. Ex: CTACCG vs. TACATG. Sol: M = x 2 -y 1, x 3 -y 2, x 4 -y 3, x 5 -y 4, x 6 -y 6. x 1 x 2 x 3 x 4 x 5 C T A C C - G - T A C A T G y 1 y 2 y 3 y 4 y 5 y 6 x 6 11

Sequence Alignment: Problem Structure Def. OPT(i, j) = min cost of aligning strings x 1 x 2. . . xi and y 1 y 2. . . yj. Case 1: OPT matches xi-yj. – pay mismatch for xi-yj + min cost of aligning two strings x 1 x 2. . . xi-1 and y 1 y 2. . . yj-1 Case 2 a: OPT leaves xi unmatched. – pay gap for xi and min cost of aligning x 1 x 2. . . xi-1 and y 1 y 2. . . yj Case 2 b: OPT leaves yj unmatched. – pay gap for yj and min cost of aligning x 1 x 2. . . xi and y 1 y 2. . . yj-1 n n n 12

Sequence Alignment: Algorithm Sequence-Alignment(m, n, x 1 x 2. . . xm, y 1 y 2. . . yn, , ) { for i = 0 to m M[0, i] = i for j = 0 to n M[j, 0] = j for i = 1 to m for j = 1 to n M[i, j] = min( [xi, yj] + M[i-1, j-1], + M[i-1, j], + M[i, j-1]) return M[m, n] } Analysis. (mn) time and space. English words or sentences: m, n 10. Computational biology: m = n = 100, 000. 10 billions ops OK, but 10 GB array? (Solution: sequence alignment in linear space) 13

Q 1: Least-cost concatenation You have a DNA sequence A of length n; you also have a “library” of shorter strings each of length m < n. Your goal is to generate a concatenation C of strings B 1, …, Bk in the library that the cost of aligning C to A is as low as possible. You can assume a gap cost δ and a mismatch cost αpq for determining the cost of alignment. 14

Answer Let A[x: y] denote the substring of A consisting of its symbols from position x to position y. Let c(x, y) be the cost of optimally aligning A[x: y] to any string in the library. Let OPT(j) be the alignment cost for the optimal solution on the string A[1: j]. OPT(j) = mint < j c(t, j) + OPT(t – 1) for j ≥ 1 OPT(0) = 0 [Essentially, t is a “breakpoint” where you choose to use a new library component. ] 15

6. 4 Knapsack Problem

Q 2: Knapsack Problem Knapsack problem. Given n objects and a "knapsack. " Item i weighs wi > 0 kilograms and has value vi > 0. Knapsack has capacity of W kilograms. Goal: fill knapsack so as to maximize total value. n n Ex: { 3, 4 } has value 40. W = 11 Item Value Weight 1 1 1 2 6 2 3 18 5 4 22 6 5 28 7 Greedy: repeatedly add item with maximum ratio vi / wi. Ex: { 5, 2, 1 } achieves only value = 35 greedy not optimal. 17

Dynamic Programming: False Start Def. OPT(i) = max profit subset of items 1, …, i. n n Case 1: OPT does not select item i. – OPT selects best of { 1, 2, …, i-1 } Case 2: OPT selects item i. – accepting item i does not immediately imply that we will have to reject other items – without knowing what other items were selected before i, we don't even know if we have enough room for i Conclusion. Need more sub-problems! 18

Dynamic Programming: Adding a New Variable Def. OPT(i, w) = max profit subset of items 1, …, i with weight limit w. n n Case 1: OPT does not select item i. – OPT selects best of { 1, 2, …, i-1 } using weight limit w Case 2: OPT selects item i. – new weight limit = w – wi – OPT selects best of { 1, 2, …, i– 1 } using this new weight limit 19

Knapsack Problem: Bottom-Up Knapsack. Fill up an n-by-W array. Input: n, w 1, …, w. N, v 1, …, v. N for w = 0 to W M[0, w] = 0 for i = 1 to n for w = 1 to W if (wi > w) M[i, w] = M[i-1, w] else M[i, w] = max {M[i-1, w], vi + M[i-1, w-wi ]} return M[n, W] 20

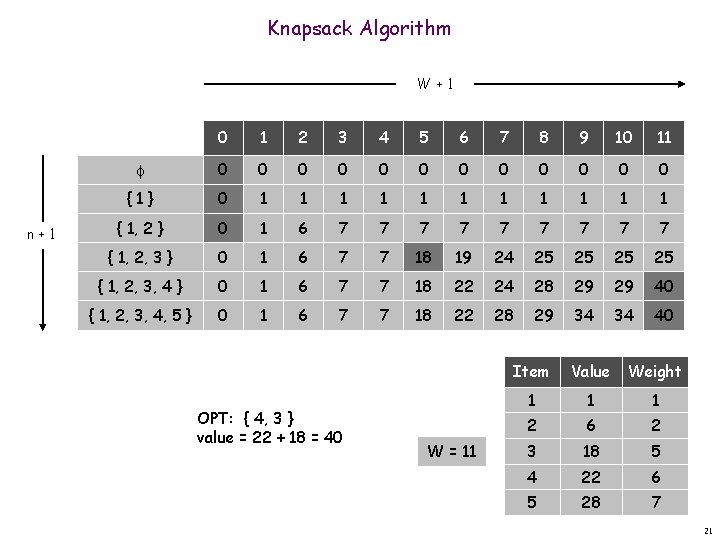
Knapsack Algorithm W+1 n+1 0 1 2 3 4 5 6 7 8 9 10 11 0 0 0 {1} 0 1 1 1 { 1, 2 } 0 1 6 7 7 7 7 7 { 1, 2, 3 } 0 1 6 7 7 18 19 24 25 25 { 1, 2, 3, 4 } 0 1 6 7 7 18 22 24 28 29 29 40 { 1, 2, 3, 4, 5 } 0 1 6 7 7 18 22 28 29 34 34 40 OPT: { 4, 3 } value = 22 + 18 = 40 W = 11 Item Value Weight 1 1 1 2 6 2 3 18 5 4 22 6 5 28 7 21

Knapsack Problem: Running Time Running time. (n W). Not polynomial in input size! "Pseudo-polynomial. " Decision version of Knapsack is NP-complete. [Chapter 8] n n n Knapsack approximation algorithm. There exists a polynomial algorithm that produces a feasible solution that has value within 0. 01% of optimum. [Section 11. 8] 22

Q 3: Longest palindromic subsequence Give an algorithm to find the longest subsequence of a given string A that is a palindrome. “amantwocamelsacrazyplanacanalpanama” 23

Q 3 -a: Palindromes (contd. ) �Every string can be decomposed into a sequence of palindromes. Give an efficient algorithm to compute the smallest number of palindromes that makes up a given string. 24