Circular Motion Highway Curves Highway Curves Banked Unbanked

Circular Motion & Highway Curves

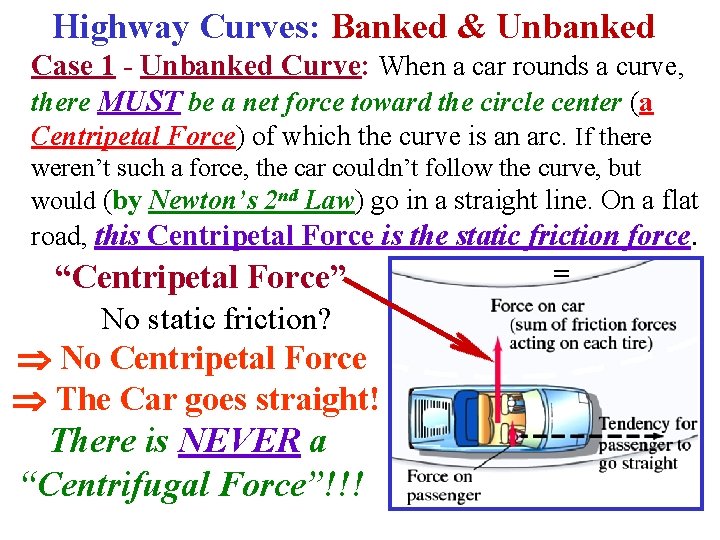
Highway Curves: Banked & Unbanked Case 1 - Unbanked Curve: When a car rounds a curve, there MUST be a net force toward the circle center (a Centripetal Force) of which the curve is an arc. If there weren’t such a force, the car couldn’t follow the curve, but would (by Newton’s 2 nd Law) go in a straight line. On a flat road, this Centripetal Force is the static friction force. = “Centripetal Force” No static friction? No Centripetal Force The Car goes straight! There is NEVER a “Centrifugal Force”!!!

Centripetal Acceleration: Car on a Curve • A car rounding a curve travels in an approximate circle. The radius of this circle is called the radius of curvature. • Forces in the y-direction – Gravity and the normal force • Forces in the x-direction – Friction is directed toward the center of the circle • Since friction is the only force acting in the xdirection, it supplies the centripetal force:

Centripetal Acceleration: Car on a Curve • A car rounding a curve travels in an approximate circle. The radius of this circle is called the radius of curvature. • Forces in the y-direction – Gravity and the normal force • Forces in the x-direction – Friction is directed toward the center of the circle • Since friction is the only force acting in the xdirection, it supplies the centripetal force: • Solving for the maximum velocity at which the car can safely round the curve gives

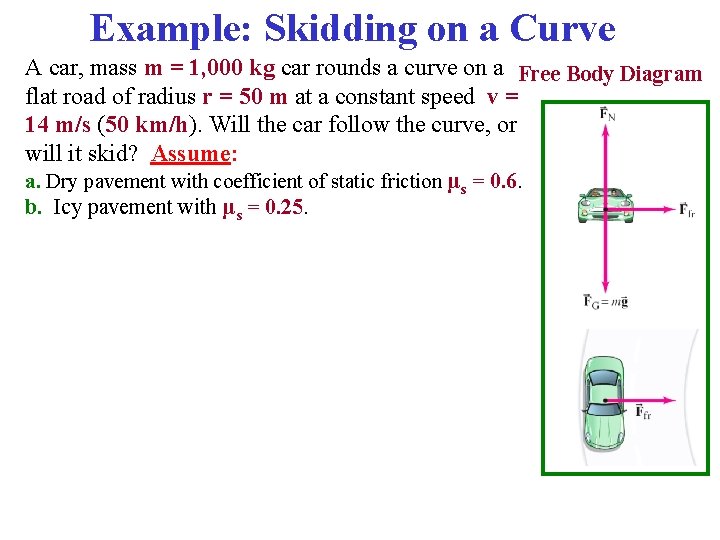
Example: Skidding on a Curve A car, mass m = 1, 000 kg car rounds a curve on a Free Body Diagram flat road of radius r = 50 m at a constant speed v = 14 m/s (50 km/h). Will the car follow the curve, or will it skid? Assume: a. Dry pavement with coefficient of static friction μs = 0. 6. b. Icy pavement with μs = 0. 25.

Example: Skidding on a Curve A car, mass m = 1, 000 kg car rounds a curve on a Free Body Diagram flat road of radius r = 50 m at a constant speed v = 14 m/s (50 km/h). Will the car follow the curve, or will it skid? Assume: a. Dry pavement with coefficient of static friction μs = 0. 6. b. Icy pavement with μs = 0. 25. Newton’s 2 nd Law: ∑F = ma x: ∑Fx = max Ffr = ma. R = m(v 2/r) y: ∑Fy = may = 0 FN - mg = 0, FN = mg Centripetal Force: m(v 2/r) = 3900 N

Example: Skidding on a Curve A car, mass m = 1, 000 kg car rounds a curve on a Free Body Diagram flat road of radius r = 50 m at a constant speed v = 14 m/s (50 km/h). Will the car follow the curve, or will it skid? Assume: a. Dry pavement with coefficient of static friction μs = 0. 6. b. Icy pavement with μs = 0. 25. Newton’s 2 nd Law: ∑F = ma x: ∑Fx = max Ffr = ma. R = m(v 2/r) y: ∑Fy = may = 0 FN - mg = 0, FN = mg Centripetal Force: m(v 2/r) = 3900 N The maximum static friction is Ffr = μs. FN a. μs = 0. 6. Maximum Ffr = 5900 N (It stays on the curve!)

Example: Skidding on a Curve A car, mass m = 1, 000 kg car rounds a curve on a Free Body Diagram flat road of radius r = 50 m at a constant speed v = 14 m/s (50 km/h). Will the car follow the curve, or will it skid? Assume: a. Dry pavement with coefficient of static friction μs = 0. 6. b. Icy pavement with μs = 0. 25. Newton’s 2 nd Law: ∑F = ma x: ∑Fx = max Ffr = ma. R = m(v 2/r) y: ∑Fy = may = 0 FN - mg = 0, FN = mg Centripetal Force: m(v 2/r) = 3900 N The maximum static friction is Ffr = μs. FN a. μs = 0. 6. Maximum Ffr = 5900 N (It stays on the curve!) b. μs = 0. 25. Maximum Ffr = 2500 N (It skids off the curve!)

If the friction force isn’t sufficient, the car will tend to move more nearly in a straight line (Newton’s 1 st Law) as the skid marks show. As long as the tires don’t slip, the friction is static. If the tires start to slip, the friction is kinetic, which is bad in 2 ways!! 1. The kinetic friction force is smaller than the static friction force. 2. The static friction force points toward the circle center, but the kinetic friction force opposes the direction of motion, making it difficult to regain control of the car & continue around the curve.

Example: Car on Banked Curve • The maximum speed can be increased by banking the curve. Assume no friction between tires & the road. So, the only forces on the car are gravity & the normal force. • The centripetal force is the horizontal component of the normal force. For every banked curve, there is one speed v at which the Centripetal Force is the horizontal component of the normal force N, so that no friction is required!! Let the horizontal be the x-direction.

Example: Car on Banked Curve • The maximum speed can be increased by banking the curve. Assume no friction between tires & the road. So, the only forces on the car are gravity & the normal force. • The centripetal force is the horizontal component of the normal force. For every banked curve, there is one speed v at which the Centripetal Force is the horizontal component of the normal force N, so that no friction is required!! Let the horizontal be the x-direction. Newton’s 2 nd Law x-direction: ∑Fx = ma. C Nx = Nsin θ = m(v 2/r) (1) y-direction: ∑Fy = may = 0 Ny - mg = 0, but Ny = Ncosθ So, Ncosθ = mg, which gives N = (mg/cosθ) (2)

Example: Car on Banked Curve • The maximum speed can be increased by banking the curve. Assume no friction between tires & the road. So, the only forces on the car are gravity & the normal force. • The centripetal force is the horizontal component of the normal force. For every banked curve, there is one speed v at which the Centripetal Force is the horizontal component of the normal force N, so that no friction is required!! Let the horizontal be the x-direction. Newton’s 2 nd Law x-direction: ∑Fx = ma. C Nx = Nsin θ = m(v 2/r) (1) y-direction: ∑Fy = may = 0 Ny - mg = 0, but Ny = Ncosθ So, Ncosθ = mg, which gives N = (mg/cosθ) (2) • Put (2) into (1): g(sinθ/cosθ) = (v 2/r) or tanθ = (v 2/gr) So,

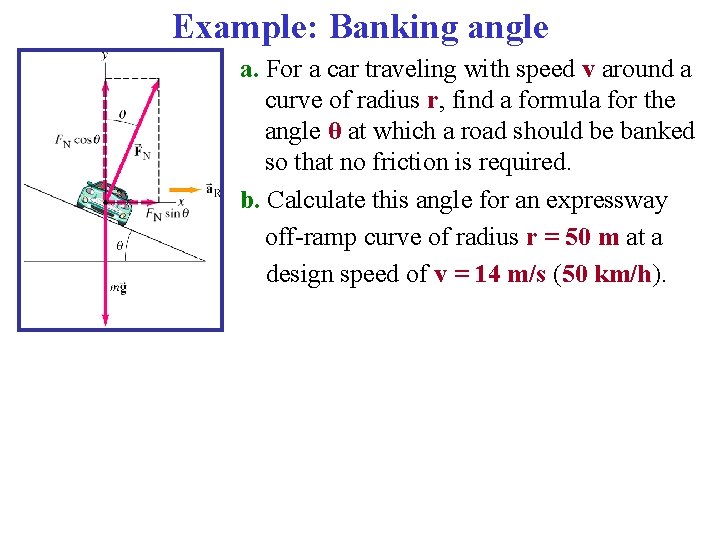
Example: Banking angle a. For a car traveling with speed v around a curve of radius r, find a formula for the angle θ at which a road should be banked so that no friction is required. b. Calculate this angle for an expressway off-ramp curve of radius r = 50 m at a design speed of v = 14 m/s (50 km/h).

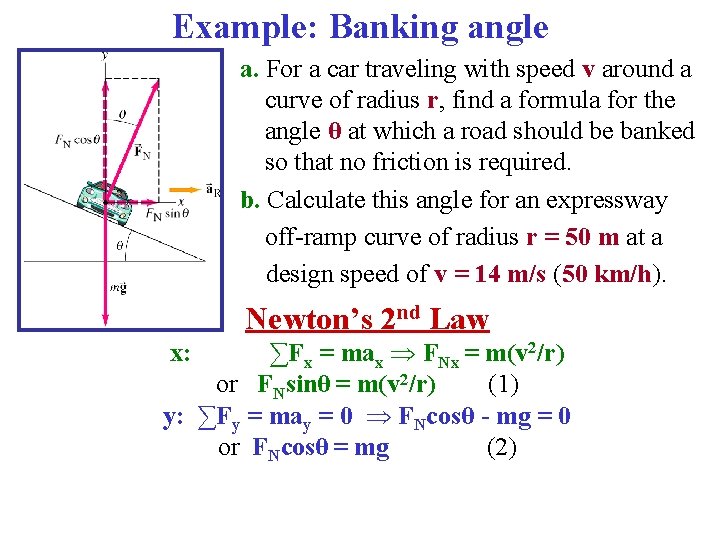
Example: Banking angle a. For a car traveling with speed v around a curve of radius r, find a formula for the angle θ at which a road should be banked so that no friction is required. b. Calculate this angle for an expressway off-ramp curve of radius r = 50 m at a design speed of v = 14 m/s (50 km/h). Newton’s 2 nd Law ∑Fx = max FNx = m(v 2/r) or FNsinθ = m(v 2/r) (1) y: ∑Fy = may = 0 FNcosθ - mg = 0 or FNcosθ = mg (2) x:

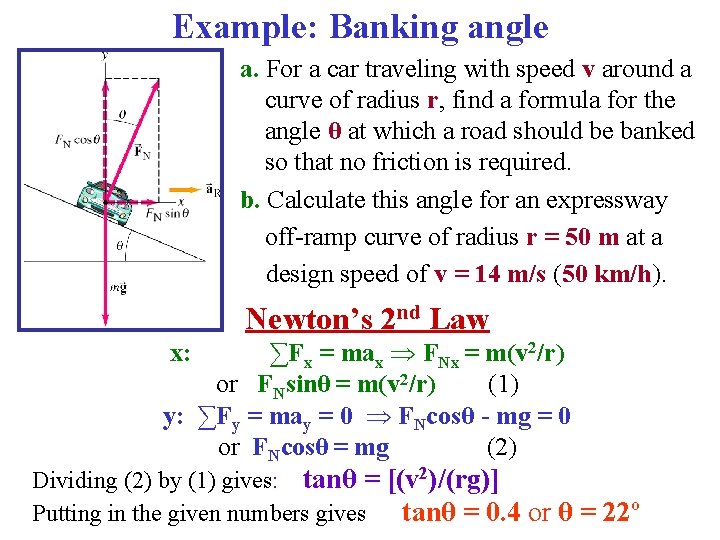
Example: Banking angle a. For a car traveling with speed v around a curve of radius r, find a formula for the angle θ at which a road should be banked so that no friction is required. b. Calculate this angle for an expressway off-ramp curve of radius r = 50 m at a design speed of v = 14 m/s (50 km/h). Newton’s 2 nd Law ∑Fx = max FNx = m(v 2/r) or FNsinθ = m(v 2/r) (1) y: ∑Fy = may = 0 FNcosθ - mg = 0 or FNcosθ = mg (2) x: Dividing (2) by (1) gives: tanθ = [(v 2)/(rg)] Putting in the given numbers gives tanθ = 0. 4 or θ = 22º

Circular Motion Example: Roller Coaster • The roller coaster’s path is nearly circular at the minimum or maximum points on the track. • When at the top, there is a maximum speed at which the coaster will not leave the top of the track.

Circular Motion Example: Roller Coaster • The roller coaster’s path is nearly circular at the minimum or maximum points on the track. • When at the top, there is a maximum speed at which the coaster will not leave the top of the track. Newton’s 2 nd Law • Let down be positive: ∑Fy = ma. C mg – N = (mv 2/r) (1) • v is maximized when N = 0. Solve (1) for v when N = 0.

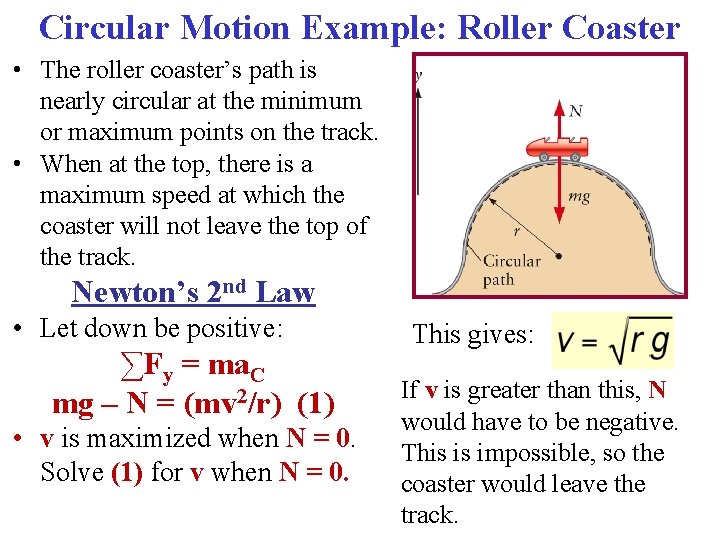
Circular Motion Example: Roller Coaster • The roller coaster’s path is nearly circular at the minimum or maximum points on the track. • When at the top, there is a maximum speed at which the coaster will not leave the top of the track. Newton’s 2 nd Law • Let down be positive: ∑Fy = ma. C mg – N = (mv 2/r) (1) • v is maximized when N = 0. Solve (1) for v when N = 0. This gives: If v is greater than this, N would have to be negative. This is impossible, so the coaster would leave the track.

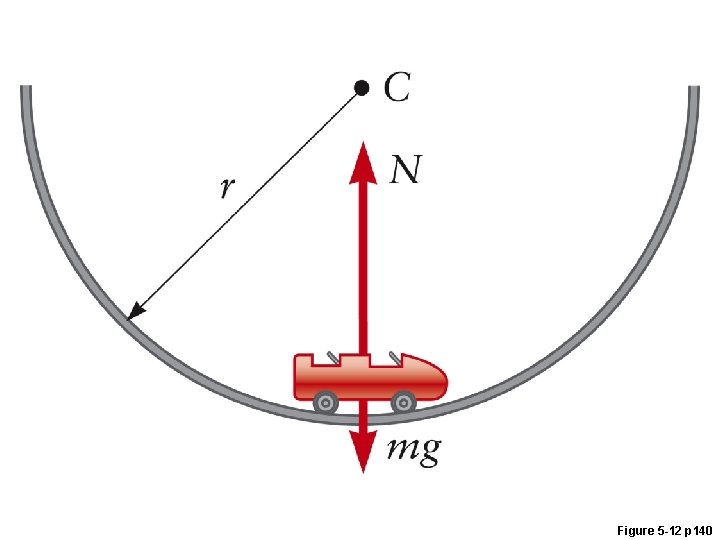
Figure 5 -12 p 140

Circular Motion Example: Artificial Gravity • Circular motion can be used to create “artificial gravity”. • The normal force acting on the passengers due to the floor would be • If N = mg it would feel like the passengers are experiencing normal Earth gravity.