CIRCULAR MOTION MEASURING CIRCULAR MOTION METHOD 1 1

MEASURING CIRCULAR MOTION (METHOD 1) 1 complete rotation = 1 revolution Measure rotational motion

MEASURING CIRCULAR MOTION (METHOD 2) 360° Can also measure using degrees 1 rotation =

MEASURING CIRCULAR MOTION (METHOD 3) Θ=s/r Radian (rad): angle with vertex at center of

CONVERTING BETWEEN DIFFERENT MEASUREMENT By definition: 1 rev = 360° = 2π rad Convert

CONVERTING FROM DEGREE TO RAD θrad=(π/180)θdegrees Convert 75 degrees to radians

ANGULAR DISPLACEMENT Distance through which any point on rotating body moves (angular distance instead

ANGULAR VELOCITY Similar to linear velocity, except instead of linear displacement, use angular displacement

EXAMPLE A motorcycle wheel turns 7200 times while being ridden for 10 min. What

LINEAR VELOCITY The linear speed on any point on rotating circle = v =

EXAMPLE: LINEAR VELOCITY A wheel of 1. 00 m radius turns at 1000 rpm.

ANGULAR ACCELERATION Angular acceleration = rate of change of angular velocity α α= Δω

EQUATIONS: LINEAR VS. ROTATIONAL MOTION Linear Motion Equations s = vavgt Rotational Motion Equations

SAMPLE CALCULATIONS To calculate various components of angular motion, click on the link listed

Slides: 14

Download presentation

CIRCULAR MOTION

MEASURING CIRCULAR MOTION (METHOD 1) 1 complete rotation = 1 revolution Measure rotational motion by counting the number of rotations Most common unit of measurement = revolution (abbreviated rev)

MEASURING CIRCULAR MOTION (METHOD 2) 360° Can also measure using degrees 1 rotation = 1 revolution = 360°

MEASURING CIRCULAR MOTION (METHOD 3) Θ=s/r Radian (rad): angle with vertex at center of circle whose sides cut off an arc on circle equal to its radius Radius = r Length of arc = s angle = 1 radian Unitless dimension – use rad to avoid confusion

CONVERTING BETWEEN DIFFERENT MEASUREMENT By definition: 1 rev = 360° = 2π rad Convert 10π rad to revolutions

CONVERTING FROM DEGREE TO RAD θrad=(π/180)θdegrees Convert 75 degrees to radians

ANGULAR DISPLACEMENT Distance through which any point on rotating body moves (angular distance instead of linear distance) Example: when a wheel makes one complete rotation, it’s angular displacement has been 1 rev, 2π rad, or 360°

ANGULAR VELOCITY Similar to linear velocity, except instead of linear displacement, use angular displacement Angular velocity = rev/time OR ω = angular displacement (θ)/time (t) Units = rad/s or rev/min ω= θ t

EXAMPLE A motorcycle wheel turns 7200 times while being ridden for 10 min. What is the angular velocity in rev/min?

LINEAR VELOCITY The linear speed on any point on rotating circle = v = ωr v = linear velocity ω = angular velocity r = radius Can measure using stroboscope or strobe light

EXAMPLE: LINEAR VELOCITY A wheel of 1. 00 m radius turns at 1000 rpm. Find the linear speed of a point on the rim of the wheel.

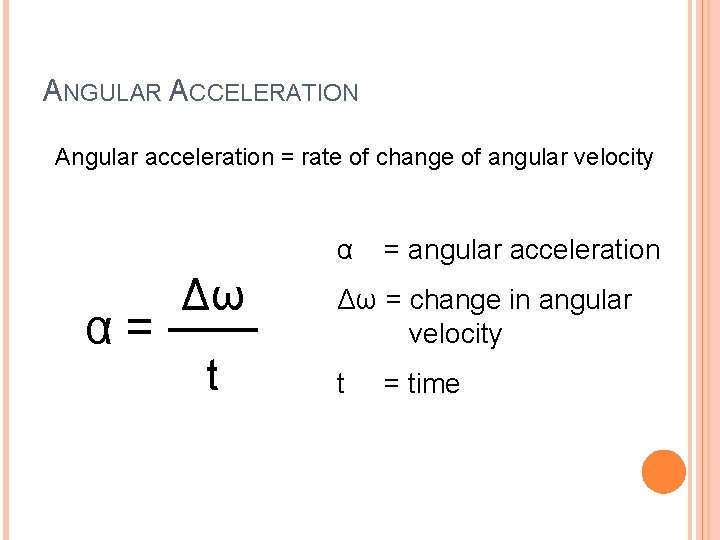
ANGULAR ACCELERATION Angular acceleration = rate of change of angular velocity α α= Δω t = angular acceleration Δω = change in angular velocity t = time

EQUATIONS: LINEAR VS. ROTATIONAL MOTION Linear Motion Equations s = vavgt Rotational Motion Equations θ = ωavgt s = vit + ½aavgt 2 θ = ωit + ½αavg t 2 vavg = (vf + vi)/t ωavg = (ωf + ωi)/t aavg = (vf – vi)/t αavg = (ωf – ωi)/t 2 aavgs = vf 2 – vi 2 2αavgθ = ωf 2 – ωi 2

SAMPLE CALCULATIONS To calculate various components of angular motion, click on the link listed below: http: //canario. iqm. unicamp. br/MATDID/Hyper. Physics/ hbase/rotq. html