Physics Example 5 11 Estimate Estimate the force

Example 5 -11 (Estimate) Estimate the force a person must exert on a string

Example 5 -12: Revolving ball (vertical circle) A ball, mass m = 0. 1

A Similar Problem r = 0. 72 m, v = 4 m/s = constant

Example: F, p. 124 A Ferris wheel rider moves in a vertical circle of

Conceptual Example A tether ball is hit so that it revolves around a pole

Example 5 -13: Conical pendulum A ball of mass m, suspended by a cord

Sect. 5 -4: Highway Curves: Banked & Unbanked Case 1: Unbanked Curve. When a

Example 5 -14: Skidding on a curve A car, mass m = 1, 000

If the friction force is insufficient, the car will tend to move more nearly

Banked Curves Banking a curve helps keep cars from skidding. For every banked curve,

Example 5 -15: Banking angle a. For a car traveling with speed v around

Slides: 16

Download presentation

Physics”

Example 5 -11 (Estimate) Estimate the force a person must exert on a string attached to a 0. 15 -kg ball to make the ball revolve in a horizontal circle of radius 0. 6 m. The ball makes 2 rev/s. Ignore the string mass. m = 0. 15 kg, r = 0. 6 m, f = 2 rev/s T = 0. 5 s Assumption: Circular path is in a horizontal plane, so φ 0 cos(φ) 1

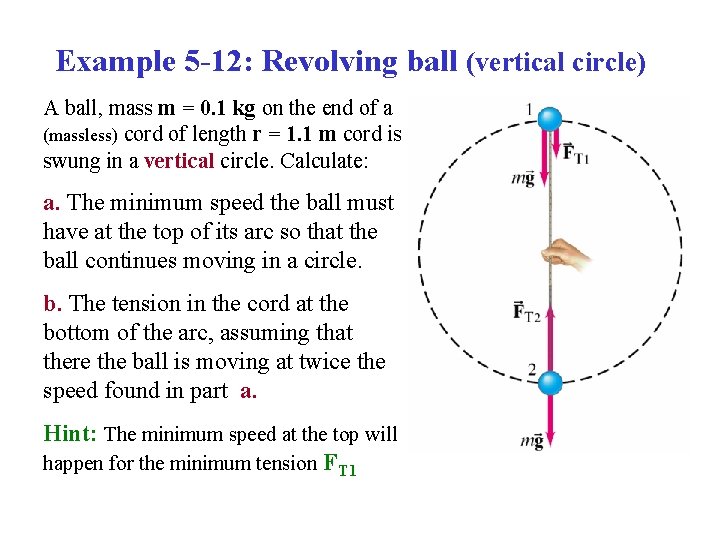
Example 5 -12: Revolving ball (vertical circle) A ball, mass m = 0. 1 kg on the end of a (massless) cord of length r = 1. 1 m cord is swung in a vertical circle. Calculate: a. The minimum speed the ball must have at the top of its arc so that the ball continues moving in a circle. b. The tension in the cord at the bottom of the arc, assuming that there the ball is moving at twice the speed found in part a. Hint: The minimum speed at the top will happen for the minimum tension FT 1

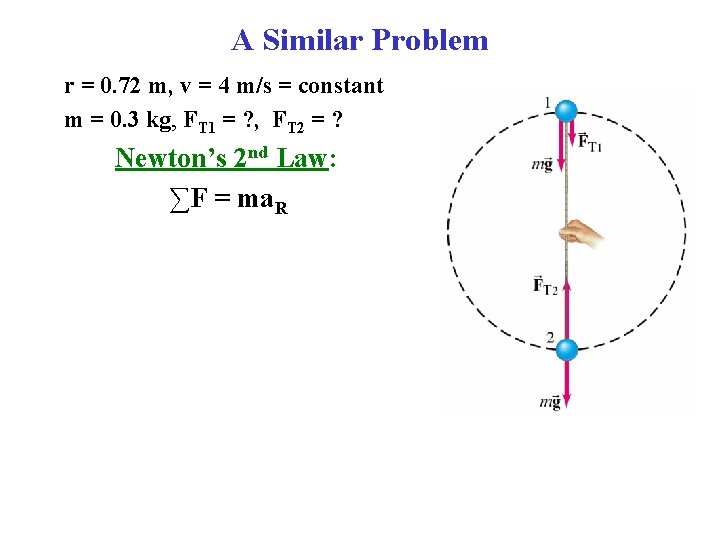
A Similar Problem r = 0. 72 m, v = 4 m/s = constant m = 0. 3 kg, FT 1 = ? , FT 2 = ? Newton’s 2 nd Law: ∑F = ma. R

A Similar Problem r = 0. 72 m, v = 4 m/s = constant m = 0. 3 kg, FT 1 = ? , FT 2 = ? Newton’s 2 nd Law: ∑F = ma. R • At the top of the circle, vertical forces: (down is positive!) FT 1 + mg = m(v 2/r) FT 1 = 3. 73 N • At the bottom of the circle, vertical forces: (up is positive!) FT 2 - mg = m(v 2/r) FT 2 = 9. 61 N

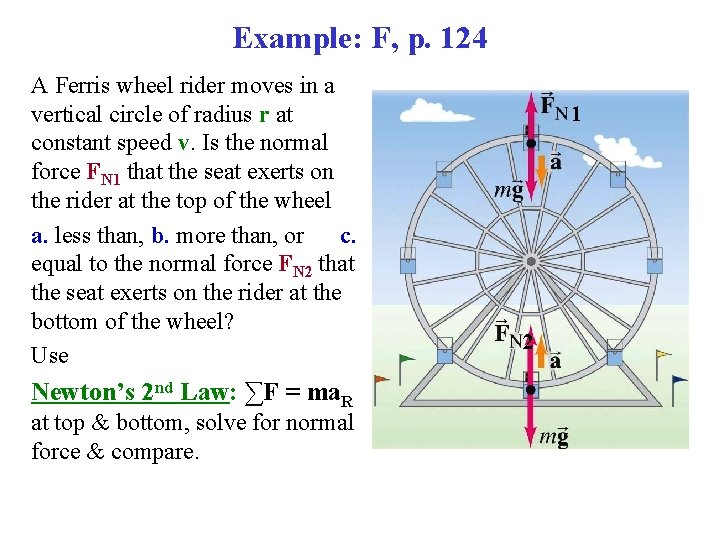
Example: F, p. 124 A Ferris wheel rider moves in a vertical circle of radius r at constant speed v. Is the normal force FN 1 that the seat exerts on the rider at the top of the wheel a. less than, b. more than, or c. equal to the normal force FN 2 that the seat exerts on the rider at the bottom of the wheel? Use Newton’s 2 nd Law: ∑F = ma. R at top & bottom, solve for normal force & compare. 1 2

Conceptual Example A tether ball is hit so that it revolves around a pole in a circle of radius r at constant speed v. In what direction is the acceleration & what force causes it? Newton’s 2 nd Law: ∑F = ma x: ∑Fx = max FTx = ma. R = m(v 2/r) y: ∑Fy = may = 0 FTy - mg = 0, FTy = mg

Example 5 -13: Conical pendulum A ball of mass m, suspended by a cord of length ℓ, revolves in a circle of radius r = ℓsinθ, where θ is the angle the string makes with the vertical. a. In what direction is the ball’s acceleration & what causes it? b. Calculate the speed & period (time for one revolution) of the ball in terms of ℓ, θ, g, & m.

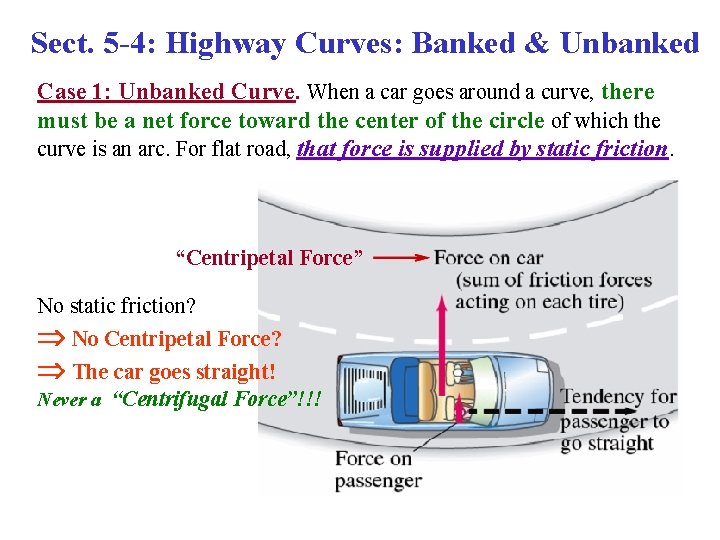
Sect. 5 -4: Highway Curves: Banked & Unbanked Case 1: Unbanked Curve. When a car goes around a curve, there must be a net force toward the center of the circle of which the curve is an arc. For flat road, that force is supplied by static friction. “Centripetal Force” No static friction? No Centripetal Force? The car goes straight! Never a “Centrifugal Force”!!!

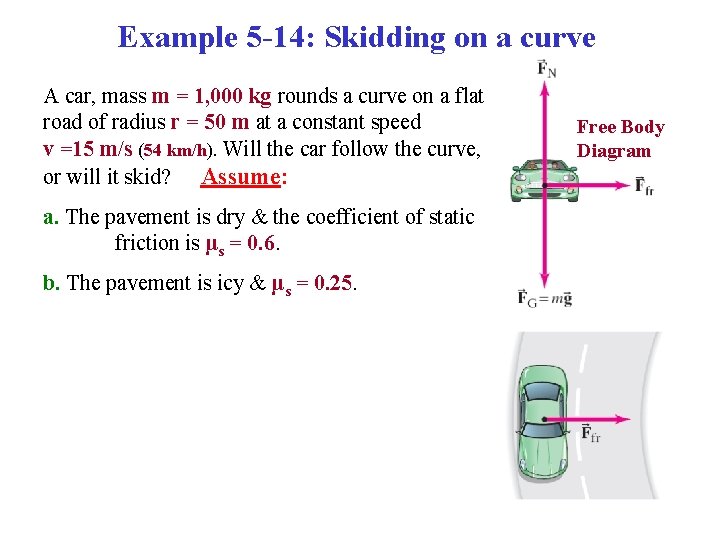
Example 5 -14: Skidding on a curve A car, mass m = 1, 000 kg rounds a curve on a flat road of radius r = 50 m at a constant speed v =15 m/s (54 km/h). Will the car follow the curve, or will it skid? Assume: a. The pavement is dry & the coefficient of static friction is μs = 0. 6. b. The pavement is icy & μs = 0. 25. Newton’s 2 nd Law: ∑F = ma x: ∑Fx = max Ffr = ma. R = m(v 2/r) y: ∑Fy = may = 0 FN - mg = 0; FN = mg Maximum static friction: Ffr = μs. FN Free Body Diagram

If the friction force is insufficient, the car will tend to move more nearly in a straight line, as the skid marks show. As long as the tires don’t slip, the friction is static. If the tires do start to slip, the friction is kinetic, which is bad in 2 ways: 1. The kinetic friction force is smaller than the static one. 2. The static friction force can point toward the center of the circle, but the kinetic friction force opposes the direction of motion, making it very difficult to regain control of the car & continue around the curve.

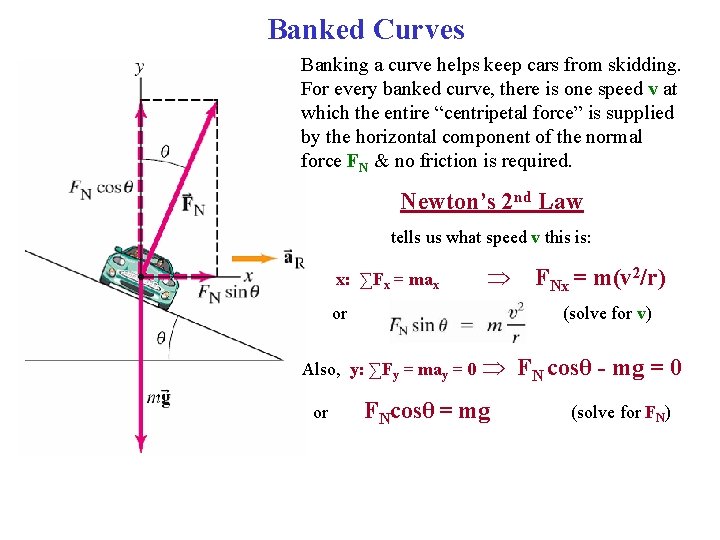
Banked Curves Banking a curve helps keep cars from skidding. For every banked curve, there is one speed v at which the entire “centripetal force” is supplied by the horizontal component of the normal force FN & no friction is required. Newton’s 2 nd Law tells us what speed v this is: x: ∑Fx = max or FNx = m(v 2/r) (solve for v) Aa Also, y: ∑Fy = may = 0 or FNcosθ = mg FN cosθ - mg = 0 (solve for FN)

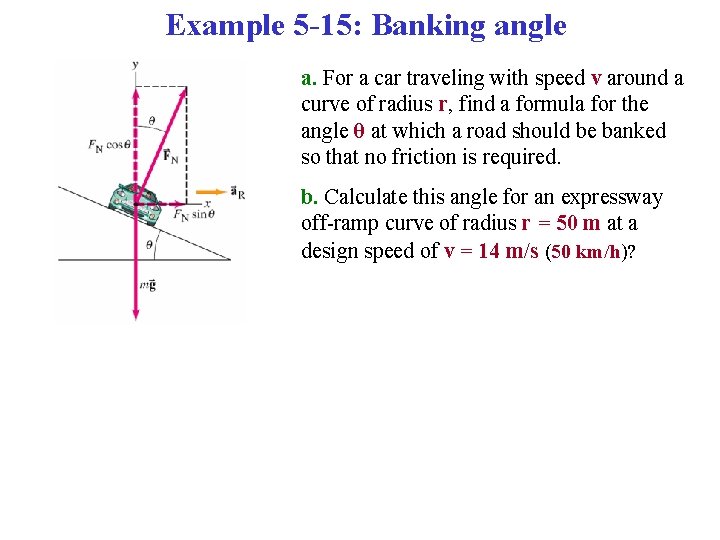
Example 5 -15: Banking angle a. For a car traveling with speed v around a curve of radius r, find a formula for the angle θ at which a road should be banked so that no friction is required. b. Calculate this angle for an expressway off-ramp curve of radius r = 50 m at a design speed of v = 14 m/s (50 km/h)? Newton’s 2 nd Law x: ∑Fx = max FNx = m(v 2/r) or FNsinθ = m(v 2/r) y: ∑Fy = may = 0 FN cosθ - mg = 0 or FNcosθ = mg tanθ = [(v 2)/(rg)] Putting in the given numbers, tanθ = 0. 4 or θ = 22º Dividing (2) by (1) gives: (1) (2)