6 Orthogonality and Least Squares 6 5 LEASTSQUARES
















- Slides: 16

6 Orthogonality and Least Squares 6. 5 LEAST-SQUARES PROBLEMS © 2012 Pearson Education, Inc.

LEAST-SQUARES PROBLEMS § Definition: If A is squares solution of for all x in and b is in , a leastis an in such that . § The most important aspect of the least-squares problem is that no matter what x we select, the vector Ax will necessarily be in the column space, Col A. § So we seek an x that makes Ax the closest point in Col A to b. See the figure on the next slide. © 2012 Pearson Education, Inc. Slide 6. 5 - 2

LEAST-SQUARES PROBLEMS § Solution of the General Least-Squares Problem § Given A and b, apply the Best Approximation Theorem to the subspace Col A. § Let © 2012 Pearson Education, Inc. Slide 6. 5 - 3

SOLUTION OF THE GENREAL LEASTSQUARES PROBLEM § Because is in the column space A, the equation is consistent, and there is an in such that ----(1) § Since is the closest point in Col A to b, a vector is a least-squares solution of if and only if satisfies (1). § Such an in is a list of weights that will build out of the columns of A. See the figure on the next slide. © 2012 Pearson Education, Inc. Slide 6. 5 - 4

SOLUTION OF THE GENREAL LEASTSQUARES PROBLEM § Suppose satisfies. § By the Orthogonal Decomposition Theorem, the projection has the property that is orthogonal to Col A, so is orthogonal to each column of A. § If aj is any column of A, then , and. © 2012 Pearson Education, Inc. Slide 6. 5 - 5

SOLUTION OF THE GENREAL LEASTSQUARES PROBLEM § Since each is a row of AT, ----(2) § Thus § These calculations show that each least-squares solution of satisfies the equation ----(3) § The matrix equation (3) represents a system of equations called the normal equations for. § A solution of (3) is often denoted by. © 2012 Pearson Education, Inc. Slide 6. 5 - 6

SOLUTION OF THE GENREAL LEASTSQUARES PROBLEM § Theorem 13: The set of least-squares solutions of coincides with the nonempty set of solutions of the normal equation. § Proof: The set of least-squares solutions is nonempty and each least-squares solution satisfies the normal equations. § Conversely, suppose satisfies. § Then satisfies (2), which shows that is orthogonal to the rows of AT and hence is orthogonal to the columns of A. § Since the columns of A span Col A, the vector is orthogonal to all of Col A. © 2012 Pearson Education, Inc. Slide 6. 5 - 7

SOLUTION OF THE GENREAL LEASTSQUARES PROBLEM § Hence the equation is a decomposition of b into the sum of a vector in Col A and a vector orthogonal to Col A. § By the uniqueness of the orthogonal decomposition, must be the orthogonal projection of b onto Col A. § That is, © 2012 Pearson Education, Inc. and is a least-squares solution. Slide 6. 5 - 8

SOLUTION OF THE GENREAL LEASTSQUARES PROBLEM § Example 1: Find a least-squares solution of the inconsistent system for § Solution: To use normal equations (3), compute: © 2012 Pearson Education, Inc. Slide 6. 5 - 9

SOLUTION OF THE GENREAL LEASTSQUARES PROBLEM § Then the equation © 2012 Pearson Education, Inc. becomes Slide 6. 5 - 10

SOLUTION OF THE GENREAL LEASTSQUARES PROBLEM § Row operations can be used to solve the system on the previous slide, but since ATA is invertible and , it is probably faster to compute and then solve © 2012 Pearson Education, Inc. as Slide 6. 5 - 11

SOLUTION OF THE GENREAL LEASTSQUARES PROBLEM § § Theorem 14: Let A be an matrix. The following statements are logically equivalent: a. The equation has a unique leastsquares solution for each b in. b. The columns of A are linearly independent. c. The matrix ATA is invertible. When these statements are true, the least-squares solution is given by ----(4) When a least-squares solution is used to produce as an approximation to b, the distance from b to is called the least-squares error of this approximation. © 2012 Pearson Education, Inc. Slide 6. 5 - 12

ALTERNATIVE CALCULATIONS OF LEAST-SQUARES SOLUTIONS § Example 2: Find a least-squares solution of for § Solution: Because the columns a 1 and a 2 of A are orthogonal, the orthogonal projection of b onto Col A is given by ----(5) © 2012 Pearson Education, Inc. Slide 6. 5 - 13

ALTERNATIVE CALCULATIONS OF LEAST-SQUARES SOLUTIONS § Now that is known, we can solve. § But this is trivial, since we already know weights to place on the columns of A to produce. § It is clear from (5) that © 2012 Pearson Education, Inc. Slide 6. 5 - 14

ALTERNATIVE CALCULATIONS OF LEAST-SQUARES SOLUTIONS § Theorem 15: Given an matrix A with linearly independent columns, let be a QR factorization of A. Then, for each b in , the equation has a unique least-squares solution, given by ----(6) § Proof: Let . § Then © 2012 Pearson Education, Inc. Slide 6. 5 - 15

ALTERNATIVE CALCULATIONS OF LEAST-SQUARES SOLUTIONS § The columns of Q form an orthonormal basis for Col A. § Hence, by Theorem 10, QQTb is the orthogonal projection of b onto Col A. § Then , which shows that is a least-squares solution of. § The uniqueness of © 2012 Pearson Education, Inc. follows from Theorem 14. Slide 6. 5 - 16
 Least squares example
Least squares example Youcubed squares and more squares answers
Youcubed squares and more squares answers Damien thiesson
Damien thiesson Inner product length and orthogonality
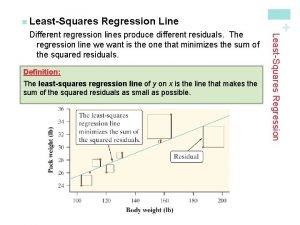
Inner product length and orthogonality Least squares regression line definition
Least squares regression line definition Residual in surveying
Residual in surveying Least squares regression line statcrunch
Least squares regression line statcrunch Least mean squares
Least mean squares Recursive least squares derivation
Recursive least squares derivation Explain the constrained least square filtering.
Explain the constrained least square filtering. 4d3d41669541f1bf19acde21e19e43d23ebbd23b
4d3d41669541f1bf19acde21e19e43d23ebbd23b Recursive least square method
Recursive least square method Least squares example
Least squares example Least squared regression line
Least squared regression line Nonlinear regression lecture notes
Nonlinear regression lecture notes Least square solution
Least square solution Qr factorization least squares
Qr factorization least squares