Regents Chemistry Physical Behavior of Matter Different Phases

Regents Chemistry Physical Behavior of Matter

Different Phases of Matter • An element, compound or mixture can exist in the form of a solid, liquid or a gas • Solid – rigid form, definite volume and shape, strong attractive forces and crystalline structure • Liquid – not held together as well, can move past one another, no definite shape but definite volume • Gas – minimal attractive forces, no definite shape or volume, expand to shape of container

Other Phases • Vapor – is the gaseous phase of a substance that is a liquid or a solid at normal conditions: ex: water vapor • Plasma – is a gas or vapor in which some or all of the electrons have been removed from the atoms. ex: In a planet’s core!

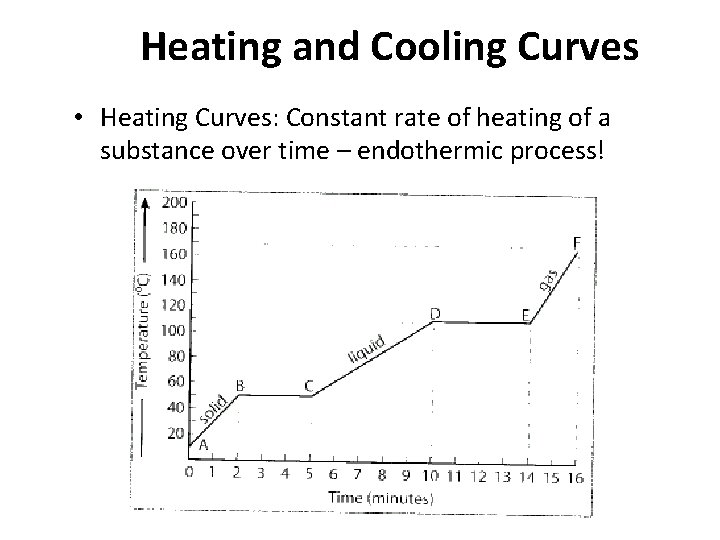
Heating and Cooling Curves • Heating Curves: Constant rate of heating of a substance over time – endothermic process!

What Can We Learn From a Heating Curve? • AB: heating of a solid, one phase present, kinetic energy increases • BC: melting of a solid (melting), two phases present, potential energy increases, kinetic energy remains constant • CD: heating of a liquid, one phase present, kinetic energy increases

What Can We Learn From a Heating Curve? • DE: boiling of a liquid (Vaporization), two phases present, potential energy increases, kinetic energy remains constant • EF: heating of a gas, one phase present, kinetic energy increases ***We can tell when the kinetic energy remains constant because the temperature is not increasing!***

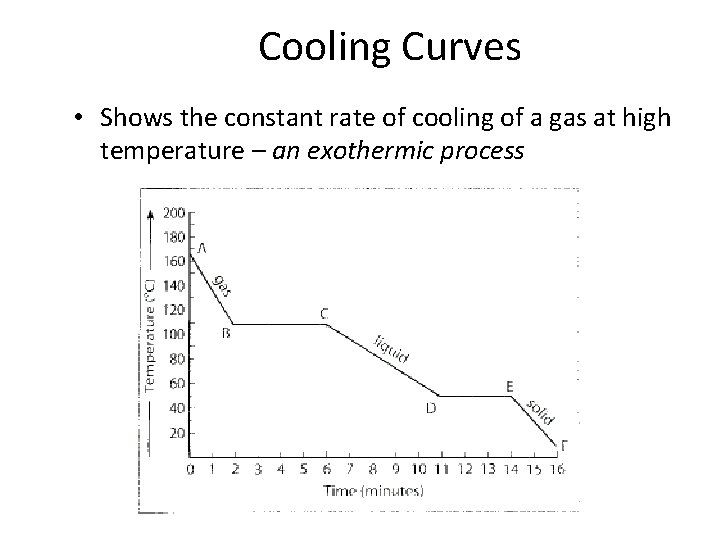
Cooling Curves • Shows the constant rate of cooling of a gas at high temperature – an exothermic process

Summary of a Cooling Curve • AB: cooling of a gas (vapor), one phase present, kinetic energy decreases • BC: condensation of the gas (vapor) to liquid, two phases present, potential energy decreases, kinetic energy remains constant • CD: cooling of a liquid, one phase present, kinetic energy decreases

Summary of a Cooling Curve • DE: solidification (freezing) of a liquid, two phases present, potential energy decreases, kinetic energy remains the same • EF: cooling of a solid, one phase present, kinetic energy decreases

Substances That Do Not Follow the Curves • Some substances change directly from a solid to a gas – Sublimation – Example: CO 2 changes from a solid to a gas a normal atmospheric pressure • Some substances change directly from gas to a solid – Deposition

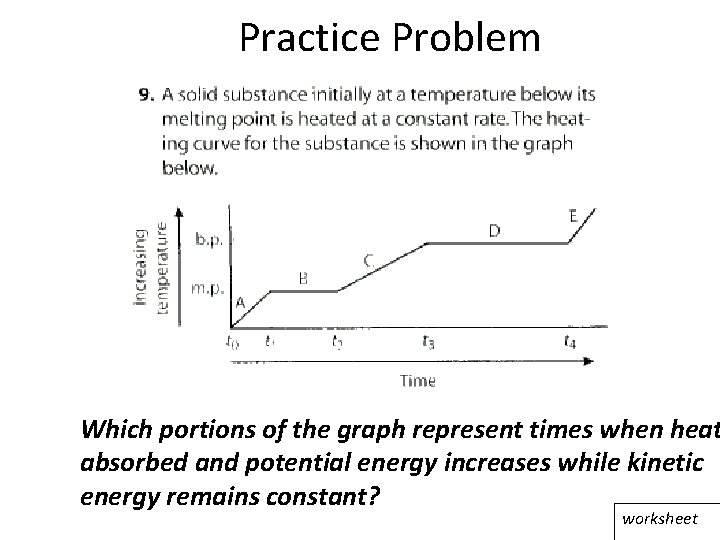
Practice Problem Which portions of the graph represent times when heat absorbed and potential energy increases while kinetic energy remains constant? worksheet

Regents Chemistry • Temperature Scales

Temperature Scales ®Celsius ® Based °C on boiling point/freezing point of water ®Kelvin ® Based K on absolute zero ®Fahrenheit ® Used °F in U. S. and Great Britain

Conversions ® Key Equations Celsius to Kelvin K = °C + 273 Fahrenheit to Celsius °C = 5/9 (°F - 32) Kelvin to Celsius °C = K - 273 Celsius to Fahrenheit °F = 9/5(°C) + 32 **Add the conversions on the right to your worksheet

Practice Problems ® Convert 10 °C to °F °F = 9/5(°C) + 32 = 9/5 (10 °C) + 32 = 50°F Convert 25°C to K K = °C + 273

Regents Chemistry • Measurement of Heat Energy

Energy and Energy Changes ® Energy is the capacity to do work. In other words, it allows us to do things! ® Energy surrounds us and is involved in all of life’s daily functions. ® It comes in many forms!

Energy and Energy Changes ® Energy can be used to change the temperature of a substance ® As we heat a substance (put in heat), the vibration of molecules in a substance increases. ® Example: When a solid is heated, the molecules vibrate until they break free and the substance melts.

Specific Heat Capacity • The specific heat capacity of a substance is the amount of heat required to raise 1 gram of the substance by 1 degree Celsius • For water it is 4. 184 J / g • Compared to other substances, water has a very high specific heat. . what does this mean?

If a substance has a high specific heat capacity… • This simply means that there will be more energy stored in every 1 gram of water. This also means it will take longer to cool down.

Specific Heat Capacities • Check out the specific heat capacities of different substances!

Measurement of Heat Energy • Question: Your pool containing 100, 000 grams of water absorbs how much heat energy when it warms from 20 °C to 30 °C? • It is easy! We use a formula on our reference tables! q = m. C T

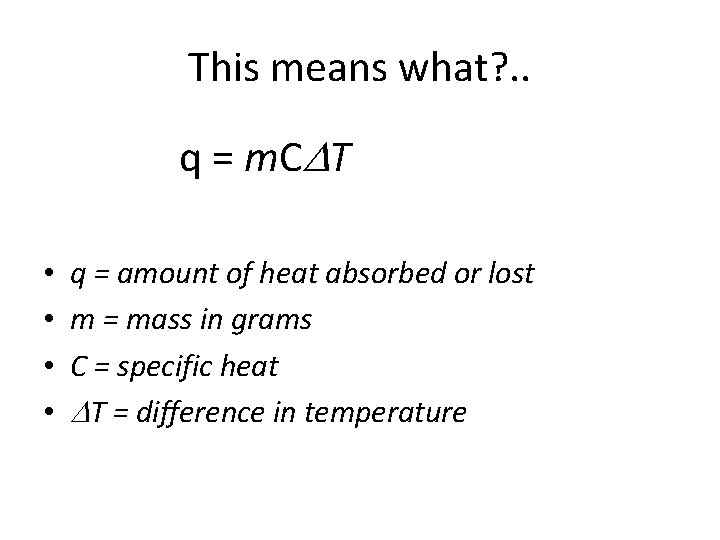
This means what? . . q = m. C T • • q = amount of heat absorbed or lost m = mass in grams C = specific heat T = difference in temperature

Back to our problem… • Question: Your pool containing 100, 000 g of water absorbs how much heat energy when it warms from 20 °C to 30 °C? • q = m. C T q = (100, 000 g)(4. 184 J / g • C) (10 °C) = q = 4, 184, 000 Joules!

Rearranging the formula. . • You need to be able to solve for any of the variables in the equation q = m. C T

Making it easy. . • If we are finding the heat change during the melting or boiling phases, we can use the Heat of Fusion or the Heat of Vaporization. . • Why? ? Because temperature remains constant during these periods!

Heat of Fusion and Vaporization • Heat of Fusion – amount of heat energy required to melt a unit mass of a substance • For water : HOF = 334 J/g • Heat of Vaporization – amount of energy required to convert a unit mass from liquid to vapor phase • For Water: HOV = 2260 J/g

Practice Problem • How many joules are required to melt 255 g of ice at 0°C? • q = m x Heat of Fusion q = 255 g x 334 J/g = 85, 170 J

Measuring Heat Change ® Calorie = the amount of energy(heat) required to raise the temperature of one gram of water by one Celsius degree. ® 1 Calorie (cal) = 4. 184 Joules (J) Metric system SI system

Converting Calories to Joules ® Convert 60. 1 cal of energy into joules 1 cal = 4. 184 J 60. 1 cal X 4. 184 J = 1 cal 251 J

Converting Joules to Calories ® Convert 50. 3 J to cal 1 cal = 4. 184 J 50. 3 J X 1 cal = 12. 0 cal 4. 184 J

Kilojoules and Kilocalories ® The prefix kilo means 1000 ® energy is often expressed in kilos because the numbers are large ® We can use Dimensional Analysis to convert. 4. 0 J x 1 k. J 1000 J = 0. 0040 k. J

Converting kilojoules to kilocalories 1 cal = 4. 184 J 1000 kcal = 4184 k. J 500. 0 k. J x 1000 kcal = 2092 kcal 4184 k. J