Geometria e Trigonometria Geometria e Trigonometria Elementos de

Geometria e Trigonometria

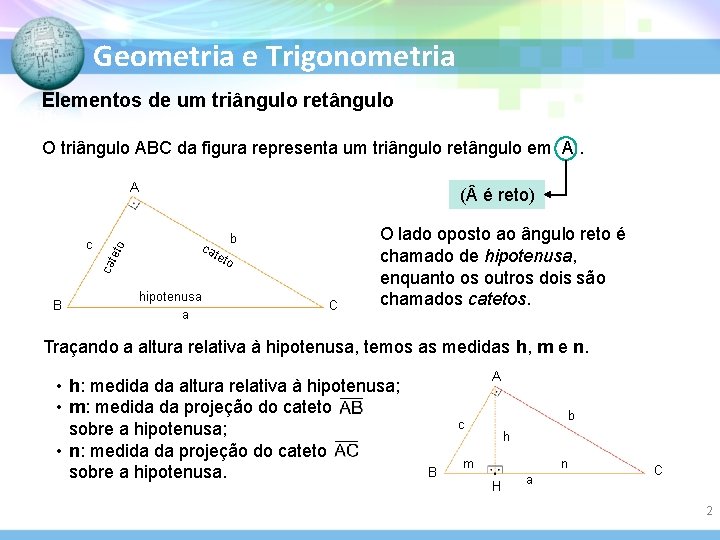
Geometria e Trigonometria Elementos de um triângulo retângulo O triângulo ABC da figura representa um triângulo retângulo em A. ca te c to A B ( é reto) b ca tet hipotenusa a o C O lado oposto ao ângulo reto é chamado de hipotenusa, enquanto os outros dois são chamados catetos. Traçando a altura relativa à hipotenusa, temos as medidas h, m e n. • h: medida da altura relativa à hipotenusa; • m: medida da projeção do cateto sobre a hipotenusa; • n: medida da projeção do cateto sobre a hipotenusa. A b c B h m n H a C 2

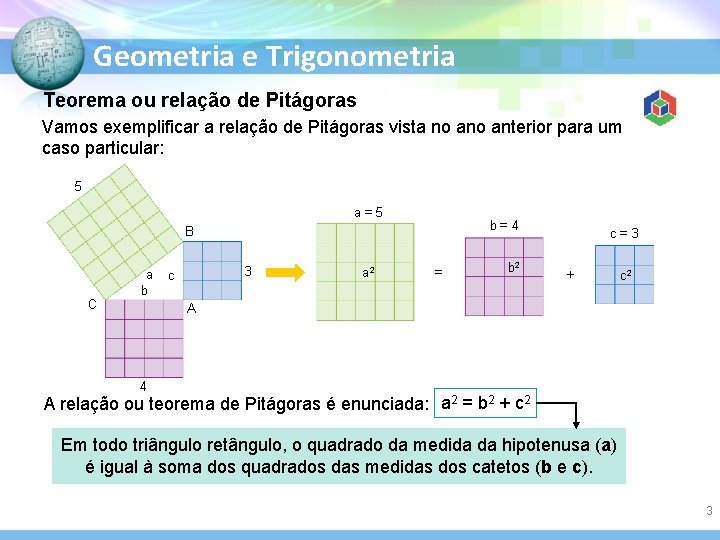
Geometria e Trigonometria Teorema ou relação de Pitágoras Vamos exemplificar a relação de Pitágoras vista no anterior para um caso particular: 5 a=5 b=4 B C a b 3 c a 2 = b 2 c=3 + c 2 A 4 A relação ou teorema de Pitágoras é enunciada: a 2 = b 2 + c 2 Em todo triângulo retângulo, o quadrado da medida da hipotenusa (a) é igual à soma dos quadrados das medidas dos catetos (b e c). 3

Geometria e Trigonometria Demonstração do teorema de Pitágoras Existem muitas formas de demonstrar esse teorema. Vejamos uma delas, baseada na semelhança de triângulos. Considere um triângulo ABC, retângulo em A, com altura hipotenusa. relativa à A b c Temos que: a = m + n 1 h B n m H C a 4

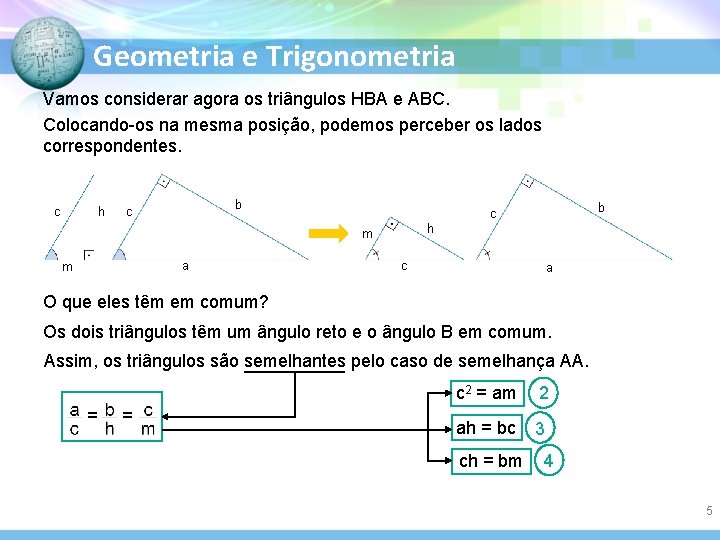
Geometria e Trigonometria Vamos considerar agora os triângulos HBA e ABC. Colocando-os na mesma posição, podemos perceber os lados correspondentes. h c b c h m a m b c c a O que eles têm em comum? Os dois triângulos têm um ângulo reto e o ângulo B em comum. Assim, os triângulos são semelhantes pelo caso de semelhança AA. = = c 2 = am 2 ah = bc 3 ch = bm 4 5

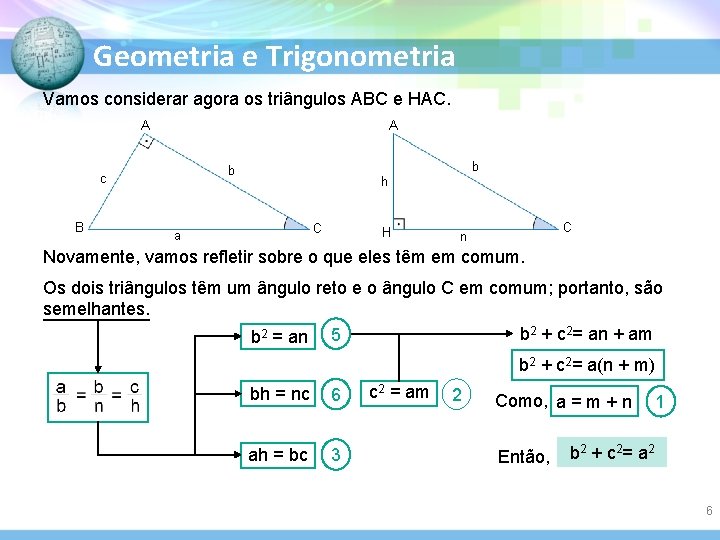
Geometria e Trigonometria Vamos considerar agora os triângulos ABC e HAC. A A B b b c h C a H C n Novamente, vamos refletir sobre o que eles têm em comum. Os dois triângulos têm um ângulo reto e o ângulo C em comum; portanto, são semelhantes. b 2 + c 2= an + am b 2 = an 5 b 2 + c 2= a(n + m) bh = nc 6 ah = bc 3 c 2 = am 2 Como, a = m + n Então, 1 b 2 + c 2 = a 2 6

Geometria e Trigonometria Outras relações métricas importantes no triângulo retângulo A A b c B m h h H H n C Assim como fizemos anteriormente, ao observar os dois triângulos podemos verificar que eles são semelhantes. Logo, = De. = = h 2 = mn , obtemos que Em qualquer triângulo retângulo, o quadrado da medida da altura relativa à hipotenusa é igual ao produto das medidas projeções dos catetos sobre a hipotenusa. 7

Geometria e Trigonometria Da demonstração do teorema de Pitágoras, você pôde notar que foram estabelecidas outras relações: c 2 = am b 2 = an O quadrado da medida de um cateto é igual ao produto da medida da hipotenusa pela medida da projeção desse cateto sobre a hipotenusa. Também da demonstração, temos outra relação: ah = bc 3 Em qualquer triângulo retângulo, o produto das medidas dos catetos é igual ao produto da medida da hipotenusa pela medida da altura relativa à hipotenusa. 8

Geometria e Trigonometria Resumindo, as relações métricas do triângulo retângulo são: h 2 = mn a=m+n ah = bc a 2 = b 2 + c 2 b c h c 2 = am m b 2 = an n a 9

Geometria e Trigonometria Aplicações importantes do teorema de Pitágoras Diagonal de um quadrado Dado um quadrado ABCD qualquer, cujo lado mede ℓ, como encontrar a medida (d) da diagonal desse quadrado em função de ℓ? O triângulo ADC é retângulo em D. A ℓ B Podemos aplicar então o teorema de Pitágoras: d 2 = ℓ 2 + ℓ 2 d 2 = 2 ℓ 2 2 d= ℓ d=ℓ ℓ ℓ d D ℓ C Portanto, a medida da diagonal de um quadrado é sempre igual ao produto da medida de um lado por. 10

Geometria e Trigonometria Altura de um triângulo equilátero Dado um triângulo equilátero ABC qualquer, cujo lado mede ℓ, como podemos encontrar a medida (h) da altura desse triângulo em função de ℓ? A O triângulo ABH é retângulo em H. Vamos aplicar o teorema de Pitágoras: h 2 + ℓ h 2 = ℓ 2 _ ℓ h 2 = ℓ 2 =ℓ 2 2 ℓ 2 h= h= ℓ ℓ ℓ ou h ou ℓ ℓ B h= ℓ. H C ℓ Portanto, a medida da altura é igual ao produto da metade da medida de um lado por. 11

Geometria e Trigonometria Diagonal de um bloco retangular Consideremos um bloco retangular cujas arestas medem a, b, c, a diagonal de uma face mede d e a diagonal do bloco mede D. O triângulo BEH é retângulo em E e sua hipotenusa mede D, mas para calculá-la precisamos encontrar o valor de d. B Aplicando o teorema de Pitágoras: d 2 = a 2 + D 2 b 2 = a 2 + b 2 + c 2 I A D 2 = d 2 + c 2 E F d a H Caso particular: diagonal do cubo O cubo é um caso particular do bloco retangular em que a = b = c = ℓ; assim: D= ℓ 2 + 2ℓ = c D D= H B I ℓ D E F d G b C A ℓ 2 = ℓ C ℓ H ℓ 12

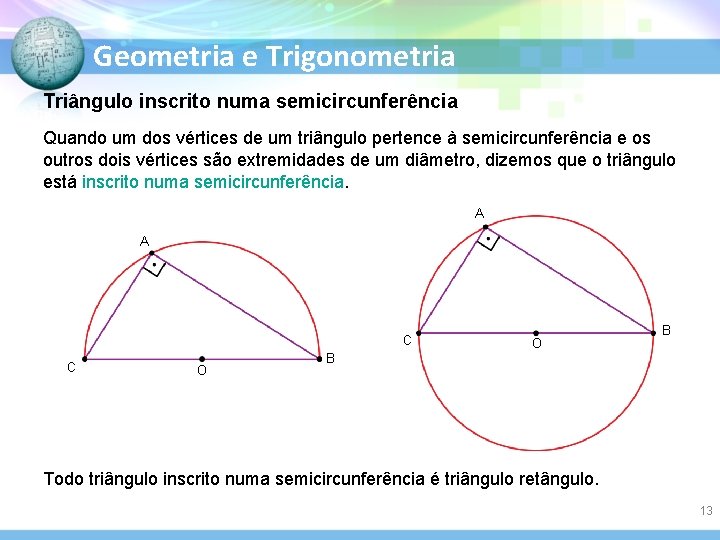
Geometria e Trigonometria Triângulo inscrito numa semicircunferência Quando um dos vértices de um triângulo pertence à semicircunferência e os outros dois vértices são extremidades de um diâmetro, dizemos que o triângulo está inscrito numa semicircunferência. A A C C O O B B Todo triângulo inscrito numa semicircunferência é triângulo retângulo. 13

Geometria e Trigonometria Outras situações que envolvem as relações métricas no triângulo retângulo Os ternos pitagóricos Ternos de números inteiros positivos a, b e c que obedecem à relação a 2 = b 2 + c 2 são chamados ternos pitagóricos. Tente pensar em um terno pitagórico! Os mais conhecidos são: 3, 4, 5 5 3 5, 12, 13 4 14

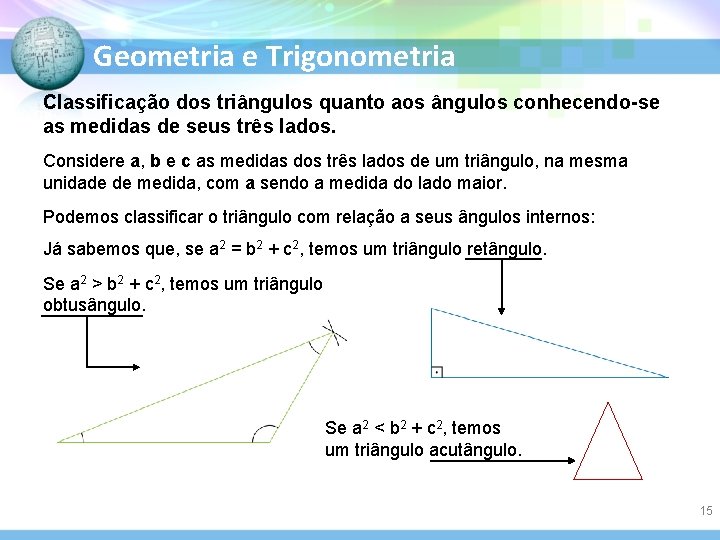
Geometria e Trigonometria Classificação dos triângulos quanto aos ângulos conhecendo-se as medidas de seus três lados. Considere a, b e c as medidas dos três lados de um triângulo, na mesma unidade de medida, com a sendo a medida do lado maior. Podemos classificar o triângulo com relação a seus ângulos internos: Já sabemos que, se a 2 = b 2 + c 2, temos um triângulo retângulo. Se a 2 > b 2 + c 2, temos um triângulo obtusângulo. Se a 2 < b 2 + c 2, temos um triângulo acutângulo. 15

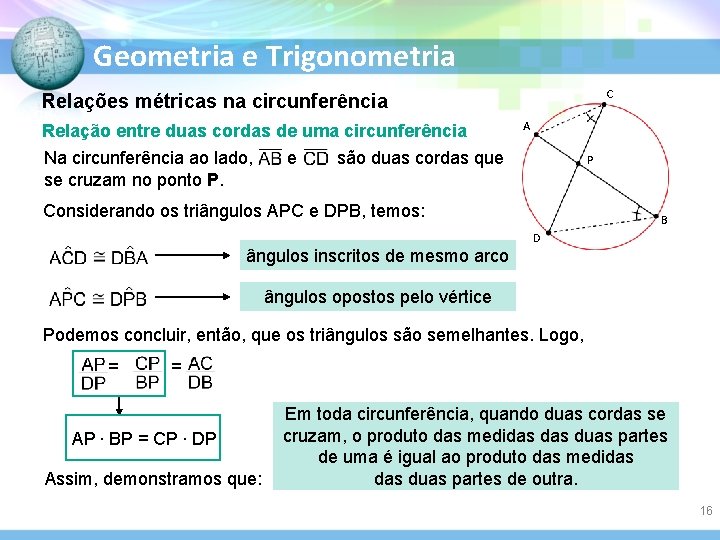
Geometria e Trigonometria C Relações métricas na circunferência Relação entre duas cordas de uma circunferência Na circunferência ao lado, se cruzam no ponto P. e A são duas cordas que P Considerando os triângulos APC e DPB, temos: B D ângulos inscritos de mesmo arco ângulos opostos pelo vértice Podemos concluir, então, que os triângulos são semelhantes. Logo, = = AP. BP = CP. DP Assim, demonstramos que: Em toda circunferência, quando duas cordas se cruzam, o produto das medidas duas partes de uma é igual ao produto das medidas duas partes de outra. 16

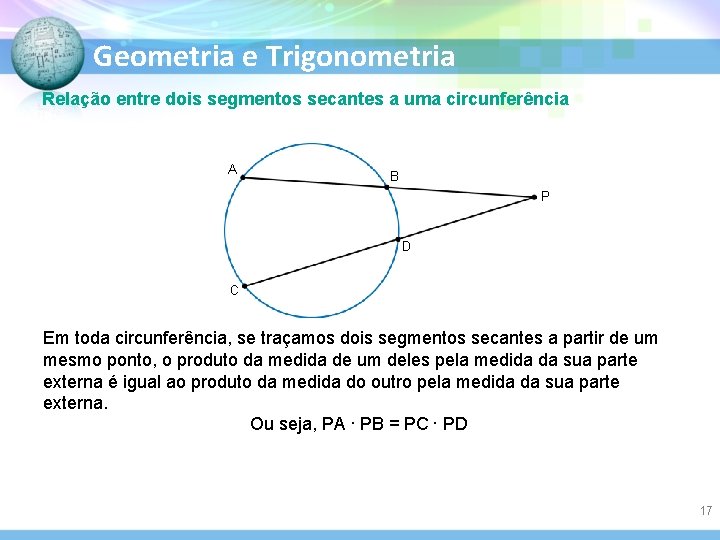
Geometria e Trigonometria Relação entre dois segmentos secantes a uma circunferência A B P D C Em toda circunferência, se traçamos dois segmentos secantes a partir de um mesmo ponto, o produto da medida de um deles pela medida da sua parte externa é igual ao produto da medida do outro pela medida da sua parte externa. Ou seja, PA. PB = PC. PD 17

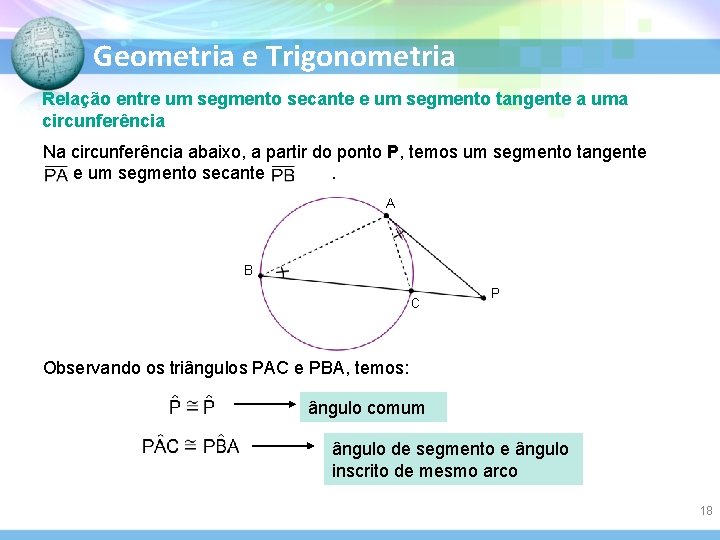
Geometria e Trigonometria Relação entre um segmento secante e um segmento tangente a uma circunferência Na circunferência abaixo, a partir do ponto P, temos um segmento tangente e um segmento secante. A B C P Observando os triângulos PAC e PBA, temos: ângulo comum ângulo de segmento e ângulo inscrito de mesmo arco 18

Geometria e Trigonometria Pelo caso AA, os triângulos PAC e PBA são semelhantes. Portanto, os lados homólogos têm medidas proporcionais: = = (PA)2 = PB. PC Em toda circunferência, se traçamos, a partir de um mesmo ponto, um segmento tangente e um segmento secante, o quadrado da medida do segmento tangente é igual ao produto da medida do segmento secante pela medida da sua parte externa. 19

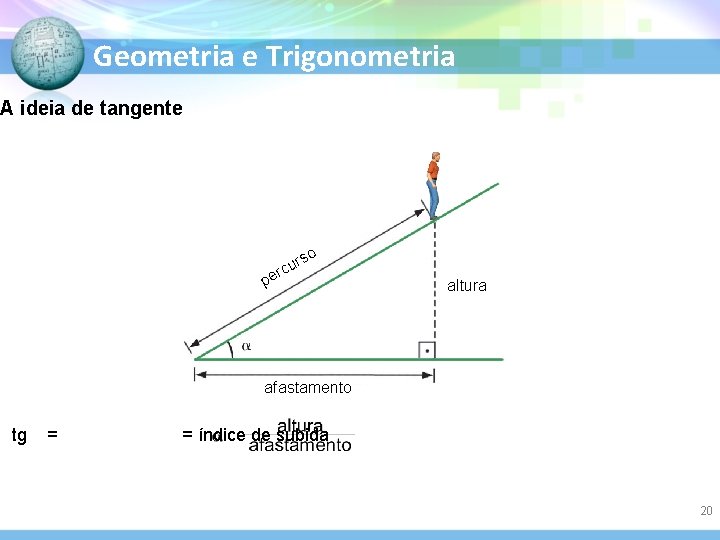
Geometria e Trigonometria A ideia de tangente rso p u erc altura afastamento tg = = índice de subida 20

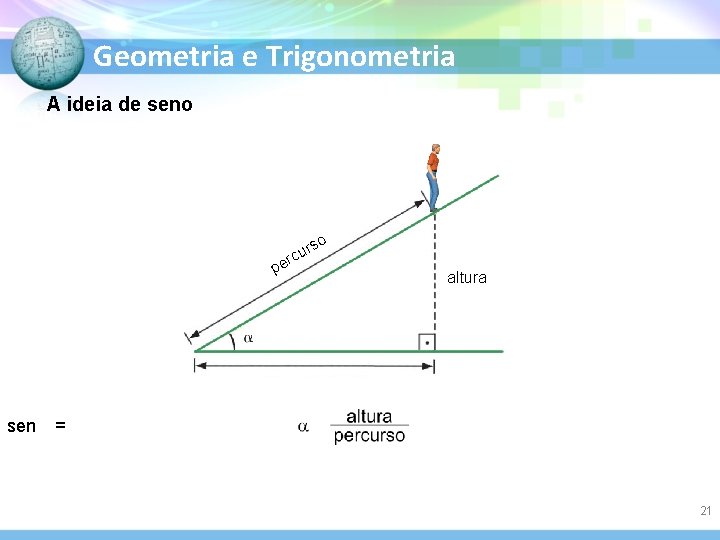
Geometria e Trigonometria A ideia de seno rs u c r pe sen o altura = 21

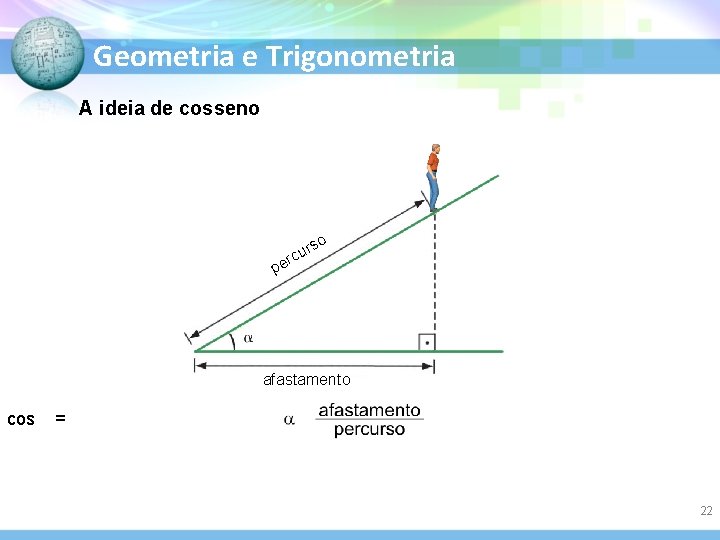
Geometria e Trigonometria A ideia de cosseno rs u c r o pe afastamento cos = 22

Geometria e Trigonometria Definição de seno, cosseno e tangente por semelhança sen θ(0º < θ < 90º) cos θ(0º < θ < 90º) tg θ(0º < θ < 90º) 23

Geometria e Trigonometria Relações entre seno, cosseno e tangente Relação fundamental sen 2 Links para ambiente online + cos 2 = + = = =1 24

Geometria e Trigonometria Relações entre seno, cosseno e tangente Outras relações = tg = = = : = sen = = cos β cos = = sen β = . tg = = = tg β 25

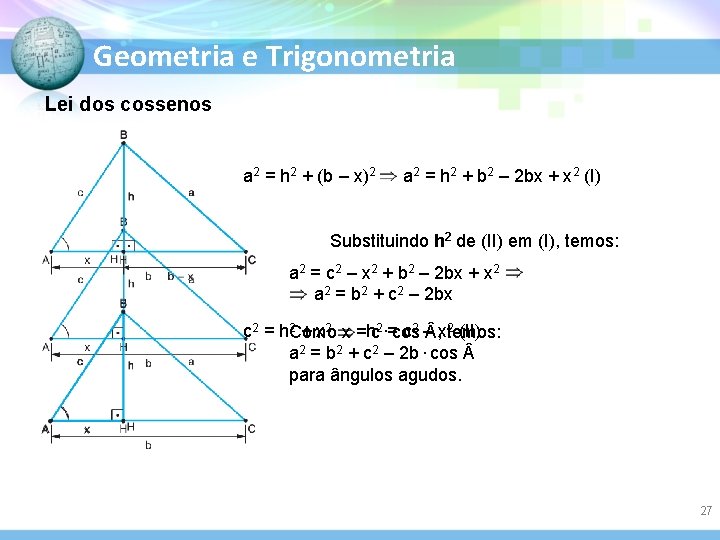
Geometria e Trigonometria Razões trigonométricas para ângulos de 30º, 45º e 60º sen cos tg 30° 45° 1 60° 26

Geometria e Trigonometria Lei dos cossenos a 2 = h 2 + (b – x)2 a 2 = h 2 + b 2 – 2 bx + x 2 (I) Substituindo h 2 de (II) em (I), temos: a 2 = c 2 – x 2 + b 2 – 2 bx + x 2 a 2 = b 2 + c 2 – 2 bx 2 + x 2 x =hc 2. =cos 2 (II) c 2 = h. Como c 2 – , xtemos: a 2 = b 2 + c 2 – 2 b. cos para ângulos agudos. 27

Geometria e Trigonometria Lei dos cossenos a 2 = h 2 + (b + x)2 a 2 = h 2 + b 2 + 2 bx + x 2 (I) Substituindo h 2 de (II) em (I), temos: a 2 = c 2 – x 2 + b 2 + 2 bx + x 2 a 2 = b 2 + c 2 + 2 bx c 2 = Como h 2 + x 2 x = ch. 2 cos = c 2 B H – x 2 e(II) o cosseno de um ângulo é igual ao oposto do cosseno do seu suplemento (cos = –cos(180º – )), temos: a 2 = b 2 + c 2 + 2 b. c. cos B H ou a 2 = b 2 + c 2 – 2 bc. cos para ângulos obtusos. 28

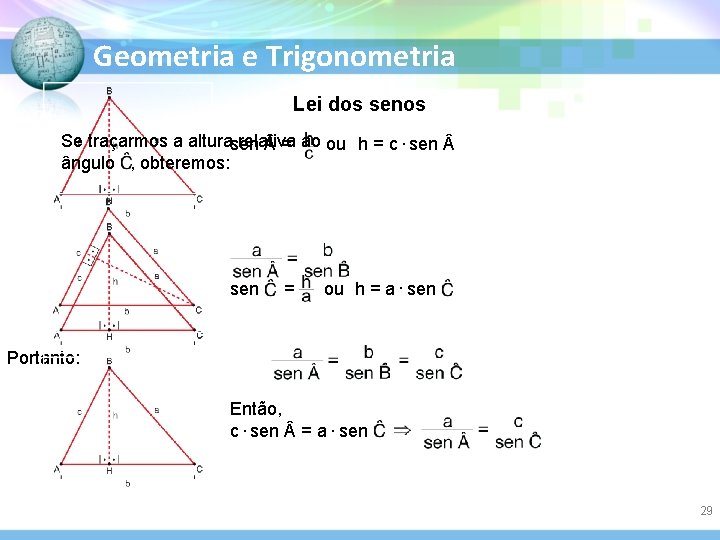
Geometria e Trigonometria Lei dos senos Se traçarmos a alturasen relativa = ao ou h = c. sen ângulo , obteremos: sen = ou h = a. sen Portanto: Então, c. sen = a. sen 29

Geometria e Trigonometria Lei dos senos Considerando a altura relativa sen =ao ângulo ou h = a. sen chegamos a: = sen (180º – ) então sen = Portanto: Então: a. sen e como sen (180º – ) = sen , ou h = c. sen 30

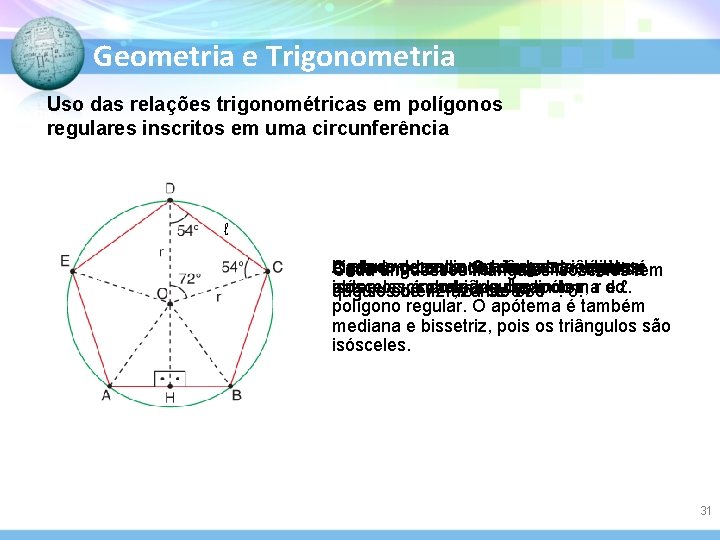
Geometria e Trigonometria Uso das relações trigonométricas em polígonos regulares inscritos em uma circunferência ℓ A altura Ligando de odesses dos centro cada cinco um O a triângulos desses todos 72 os triângulos é ângulo central mede , vértices, medida Cada um triângulos isósceles tem ˚obtidos isósceles obtemos isósceles, cinco écom chamada triângulos. de apótema e ℓ. que se obtém fazendo 360 ângulos de 72 , lados 54˚ emedindo 54. ˚ : 5. r, r do ˚ ˚ polígono regular. O apótema é também mediana e bissetriz, pois os triângulos são isósceles. 31

Geometria e Trigonometria Generalizações: hexágono, quadrado e triângulo regulares Quadrado Triângulo ℓ 6 = r , poisequilátero o triângulo é equilátero. cos 43 = 30˚ = = 2 a 6 = a 43 =a 6 = = 32