Teorema Fundamental da Trigonometria Demonstrao sen 1 sen

Teorema Fundamental da Trigonometria

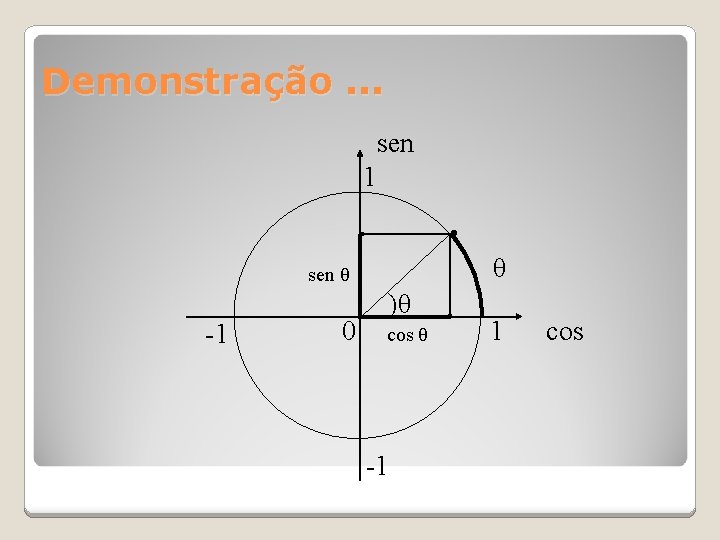
Demonstração. . . sen 1 · sen θ -1 0 )θ cos θ -1 θ 1 cos

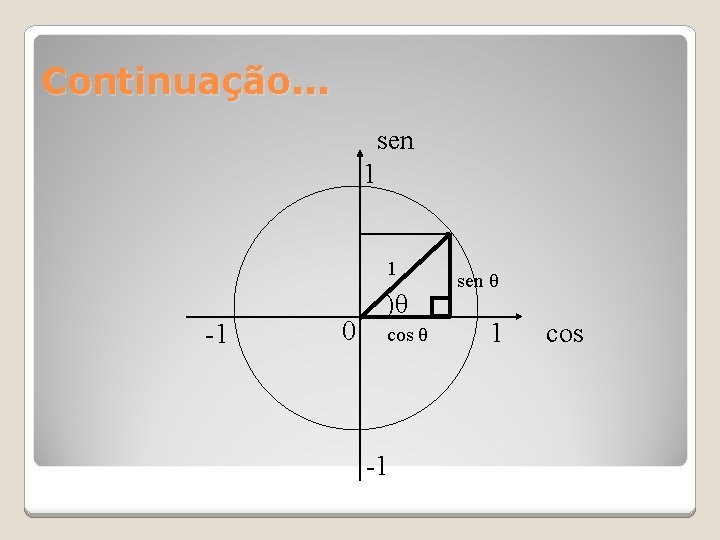
Continuação. . . sen 1 1 -1 0 )θ cos θ -1 sen θ 1 cos

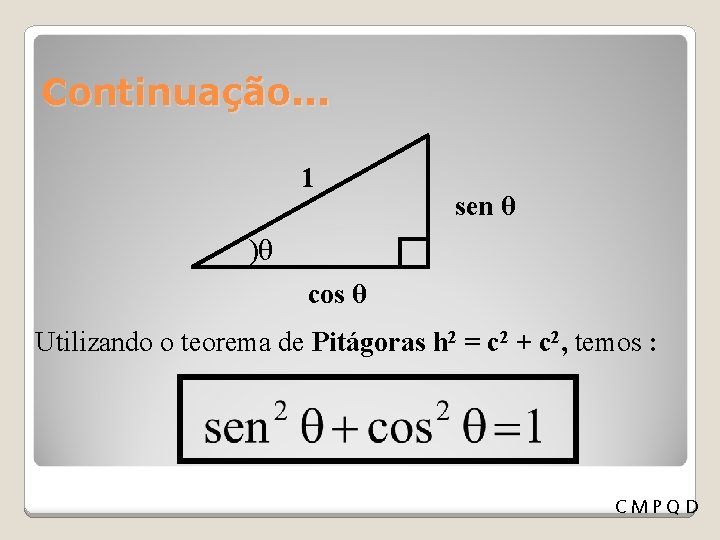
Continuação. . . 1 sen θ )θ cos θ Utilizando o teorema de Pitágoras h 2 = c 2 + c 2, temos : CMPQD

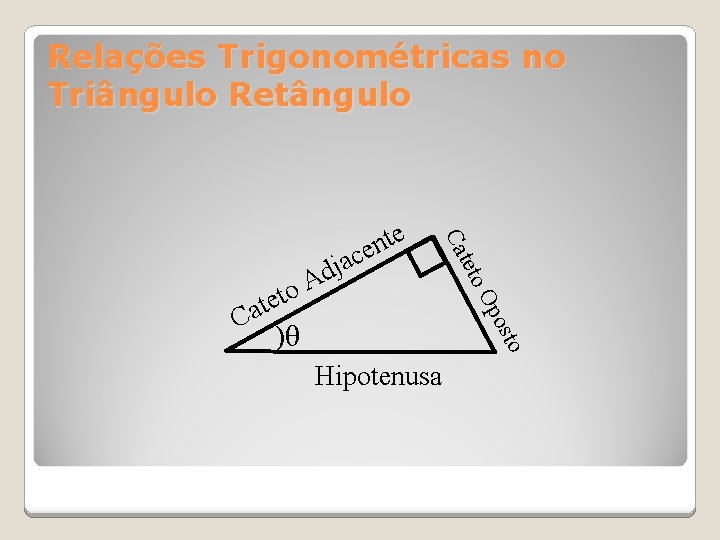
Relações Trigonométricas no Triângulo Retângulo o ost Op )θ teto C to e t a ja d A Ca e t n ce Hipotenusa

Continuação. . . Ente Trigonométrico Seno de θ Cosseno de θ Tangente de θ Cossecante de θ Secante de θ Cotangente de θ Relação no Triângulo Retângulo

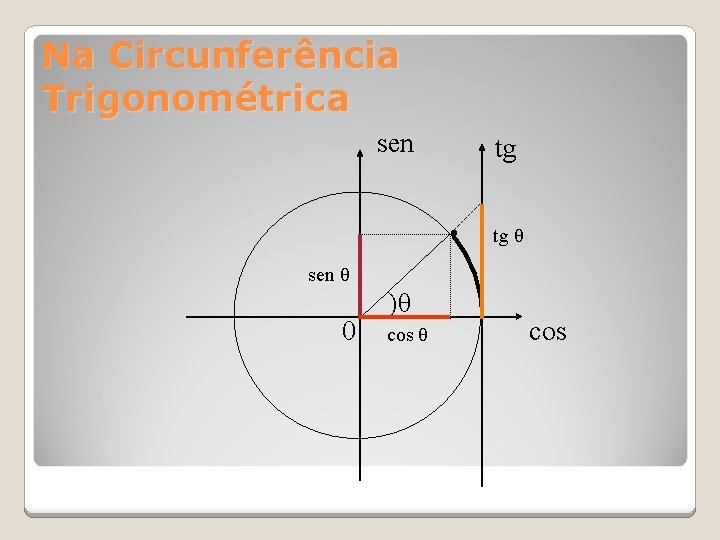
Na Circunferência Trigonométrica sen tg · tg θ sen θ 0 )θ cos

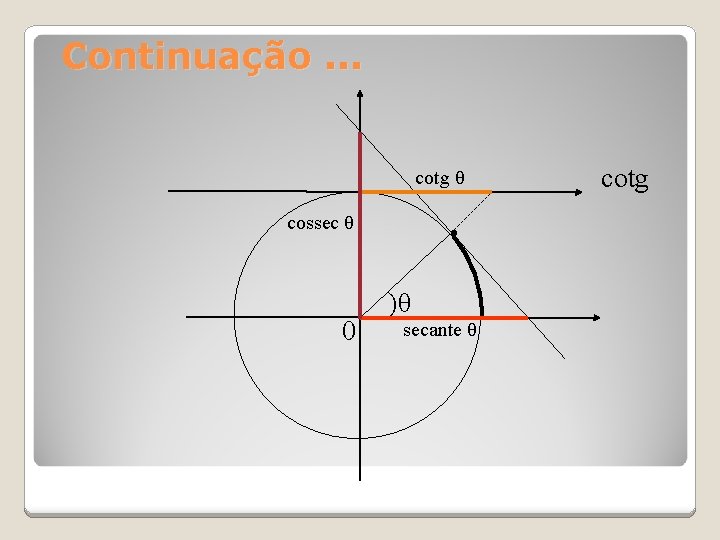
Continuação. . . cotg θ cossec θ 0 · )θ secante θ cotg

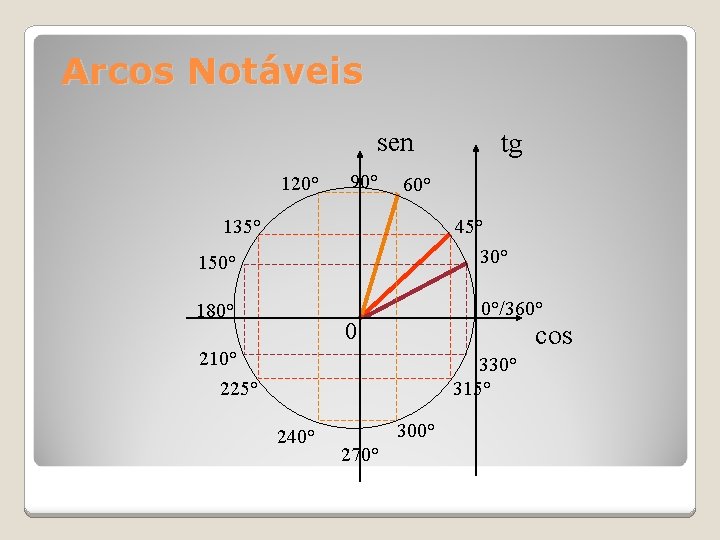
Arcos Notáveis sen 120° 90° tg 60° 135° 45° 30° 150° 180° 0°/360° 0 cos 210° 225° 330° 315° 240° 300° 270°

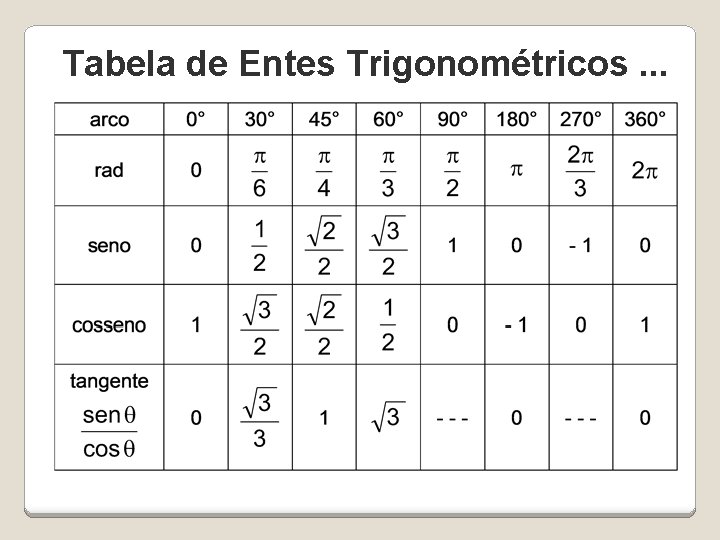
Tabela de Entes Trigonométricos. . .

Exercícios Resolvidos

Que tal fazermos um teste para verificação do que foi apresentado? Observem a figura ao lado 1) Em relação ao ângulo a, podemos dizer que o sen a vale: a) b/c b) a/c c) c/b d) c/a e) a/b

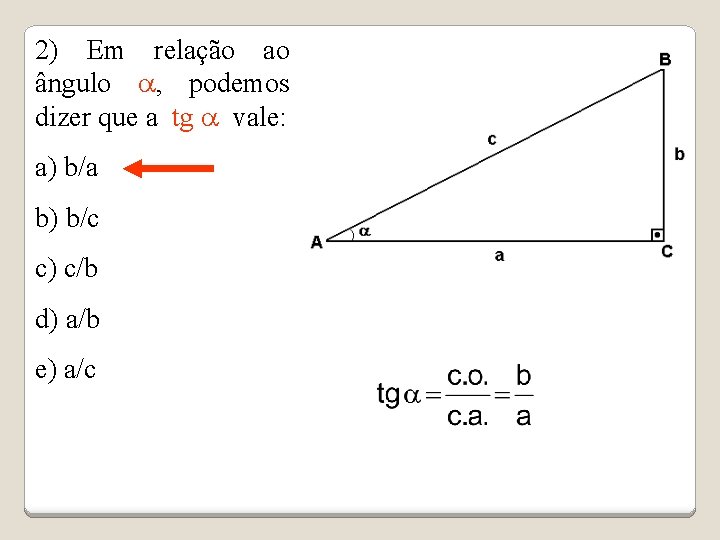
2) Em relação ao ângulo a, podemos dizer que a tg a vale: a) b/a b) b/c c) c/b d) a/b e) a/c

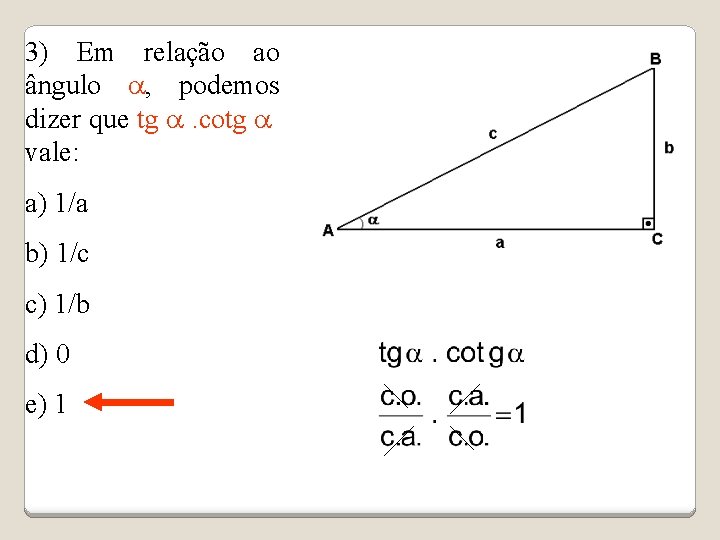
3) Em relação ao ângulo a, podemos dizer que tg a. cotg a vale: a) 1/a b) 1/c c) 1/b d) 0 e) 1

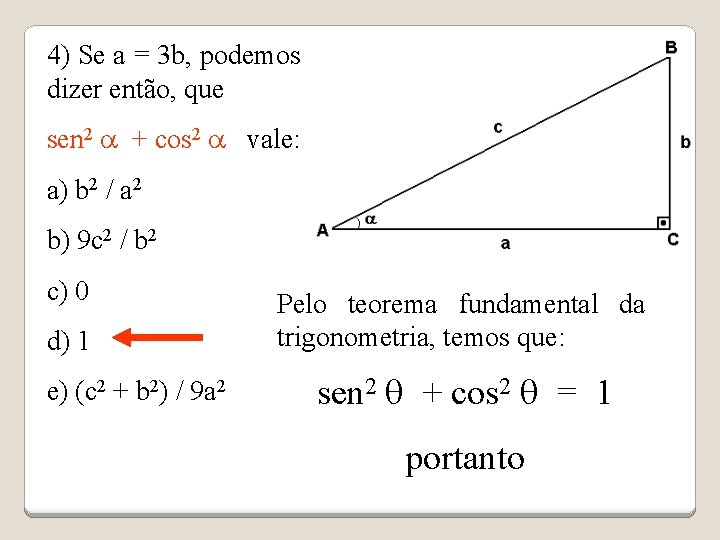
4) Se a = 3 b, podemos dizer então, que sen 2 a + cos 2 a vale: a) b 2 / a 2 b) 9 c 2 / b 2 c) 0 d) 1 e) (c 2 + b 2) / 9 a 2 Pelo teorema fundamental da trigonometria, temos que: sen 2 q + cos 2 q = 1 portanto

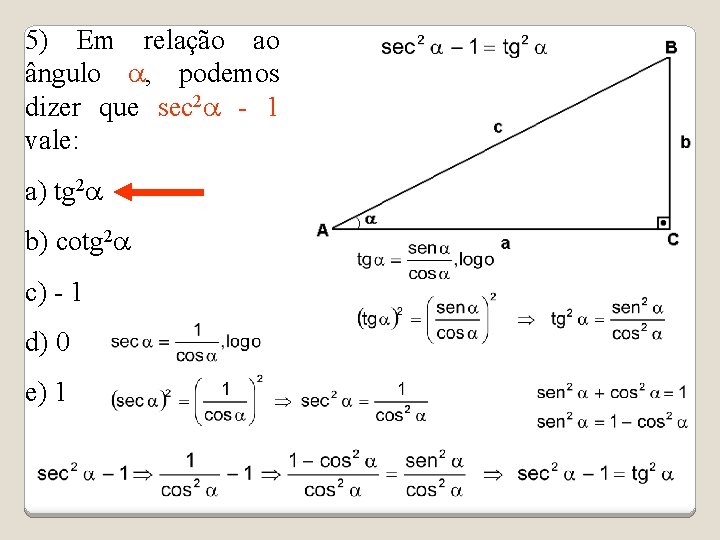
5) Em relação ao ângulo a, podemos dizer que sec 2 a - 1 vale: a) tg 2 a b) cotg 2 a c) - 1 d) 0 e) 1

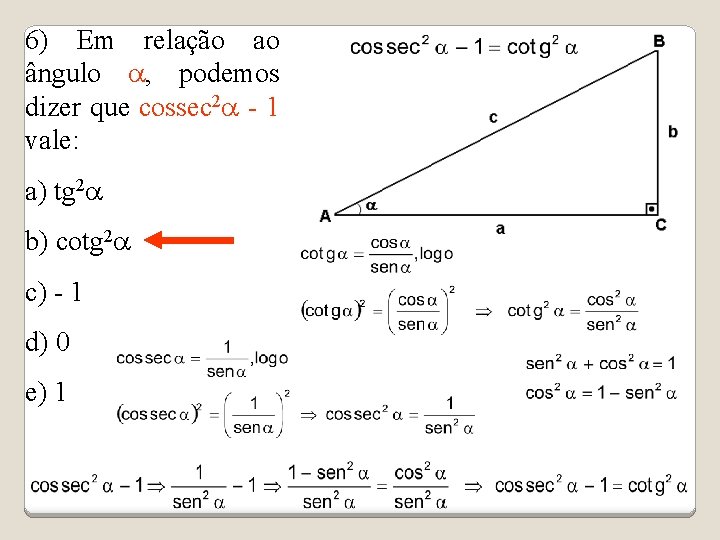
6) Em relação ao ângulo a, podemos dizer que cossec 2 a - 1 vale: a) tg 2 a b) cotg 2 a c) - 1 d) 0 e) 1

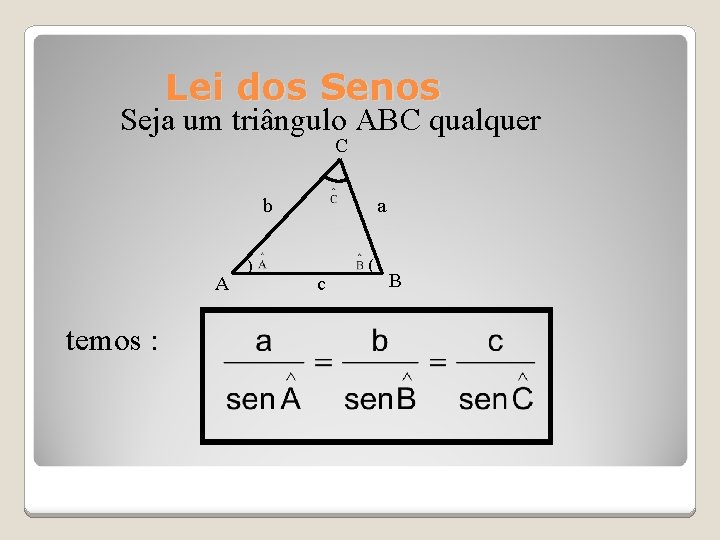
Lei dos Senos Seja um triângulo ABC qualquer C b A temos : ) a c ( B

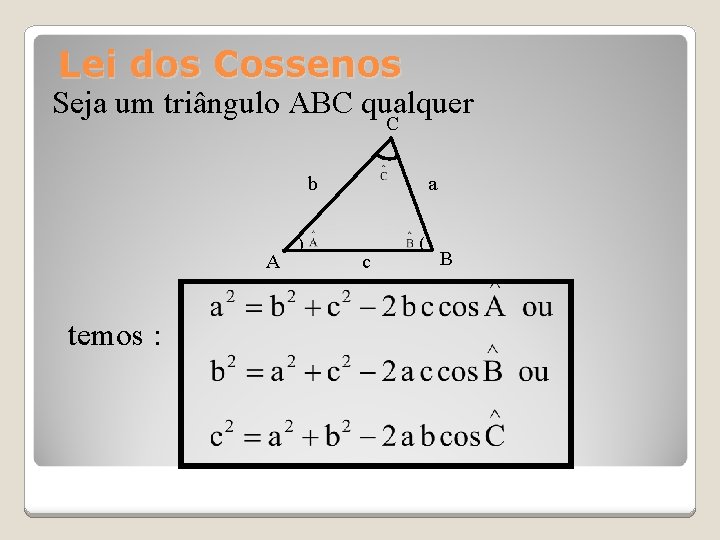
Lei dos Cossenos Seja um triângulo ABC qualquer C b A temos : ) a c ( B

Continuação. . . Curiosidade : Quando um dos ângulos do triângulo é reto, por exemplo, = 90°, temos : Sabe-se que cos 90° = 0, logo. . . Temos, portanto. . . Teorema de Pitágoras

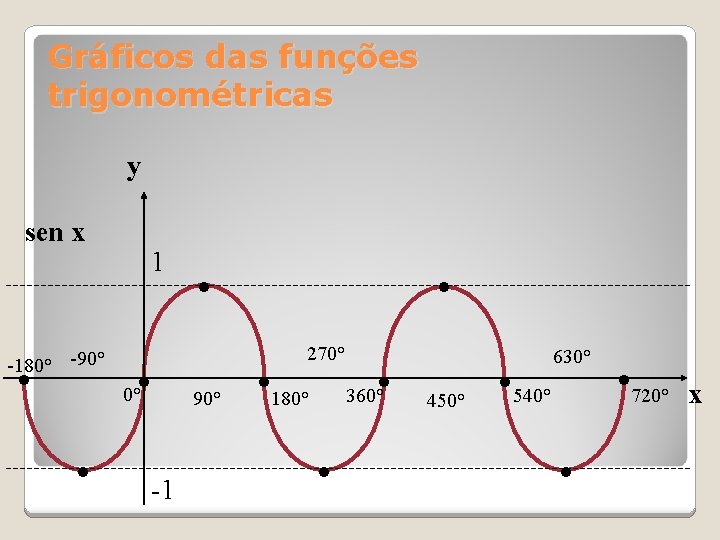
Gráficos das funções trigonométricas y sen x -180° -90° • 1 • 0° • -1 • • 270° 90° • 180° • 360° • 450° • 540° 630° • • 720° x

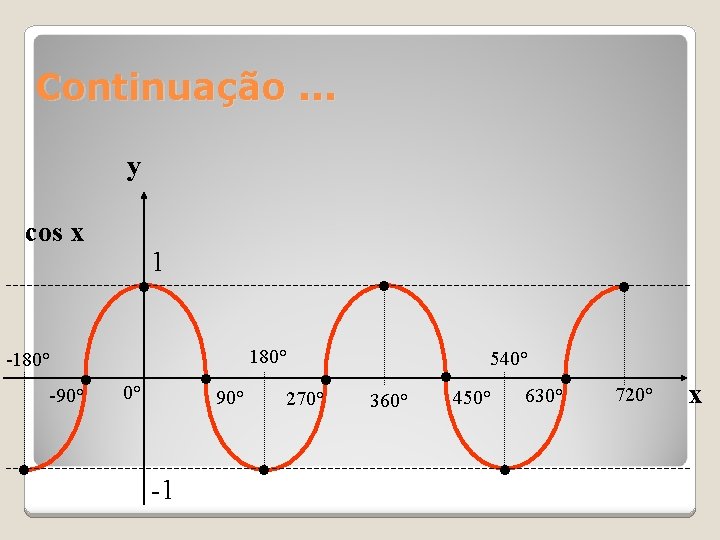
Continuação. . . y cos x • -180° • -90° • 1 • • 90° 0° -1 180° • 270° • • 540° 360° • 450° • 630° • 720° x

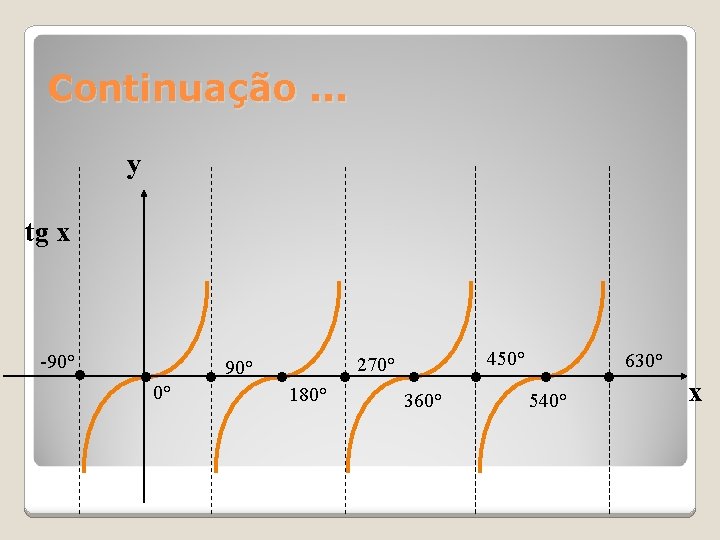
Continuação. . . y tg x -90° • • 0° • 90° • 180° • 270° • 360° • 450° • • 540° 630° x

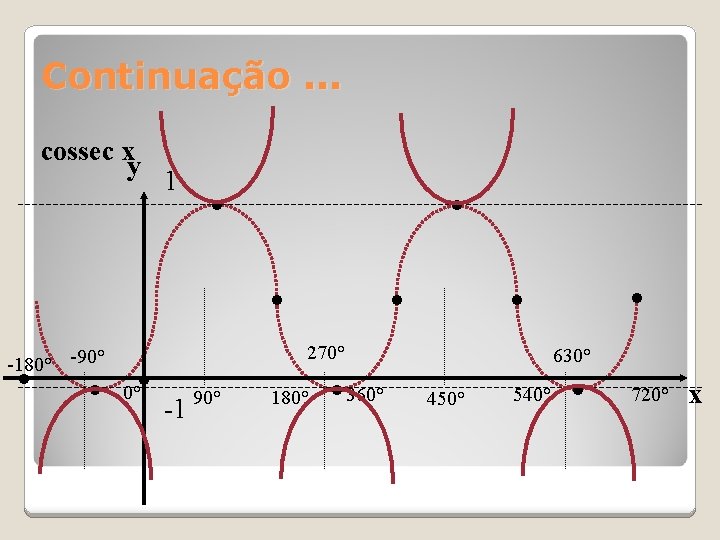
Continuação. . . cossec x y 1 • • 0° • -1 90° 180° • 360° • • 270° -180° -90° • • 630° 450° 540° • 720° x

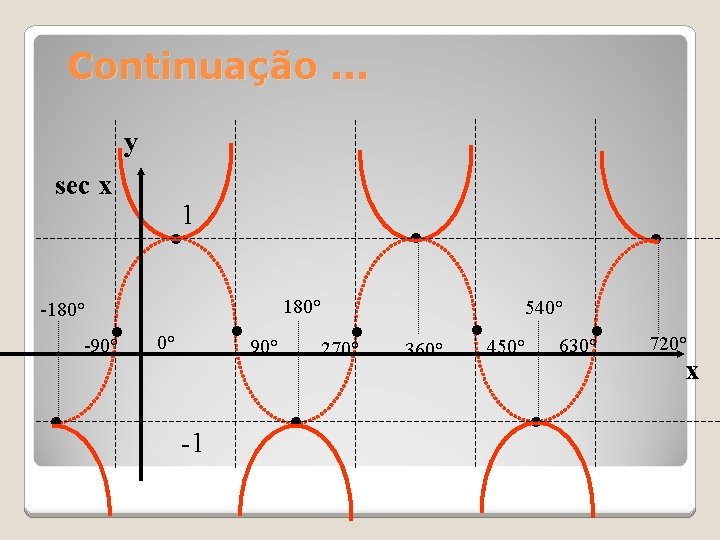
Continuação. . . y sec x 1 • • -180° • -90° • • 90° 0° -1 180° • 270° • • 540° 360° • 450° • 630° • 720° x

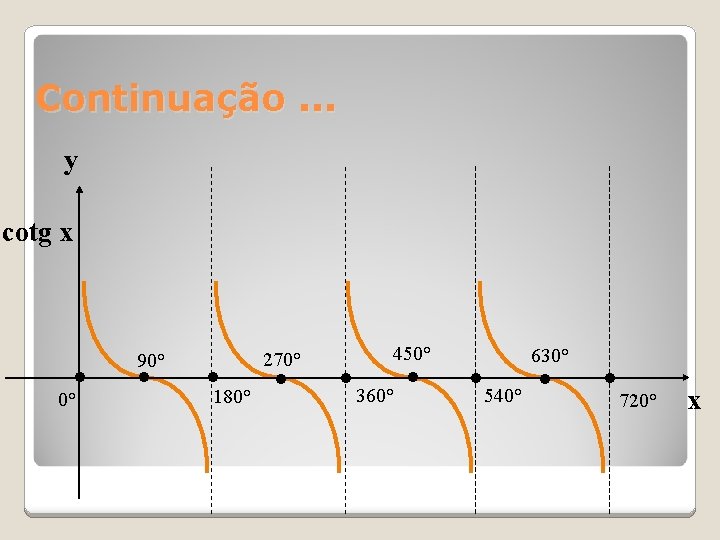
Continuação. . . y cotg x • 0° 90° • 270° • 180° • 450° • 360° • 630° • 540° • • 720° x

• Integração por Substituição trigonométrica Demonstrando o Caso I. . . CMPQD

Trigonometria Algumas Aplicações

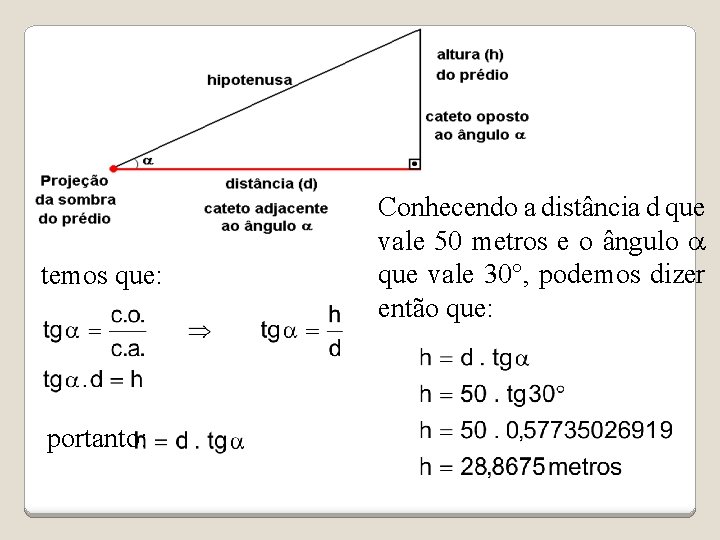
Parte Prática O exemplo clássico da Sombra Para que possamos medir (aproximadamente) a altura de um prédio, sem a necessidade de subir ao terraço, ou utilizar equipamentos sofisticados, seria necessário somente 2 elementos. São eles: uma distância um ângulo Observe a seguir. . .

temos que: portanto: Conhecendo a distância d que vale 50 metros e o ângulo a que vale 30°, podemos dizer então que:

Exemplo 1 A inclinação de uma rampa

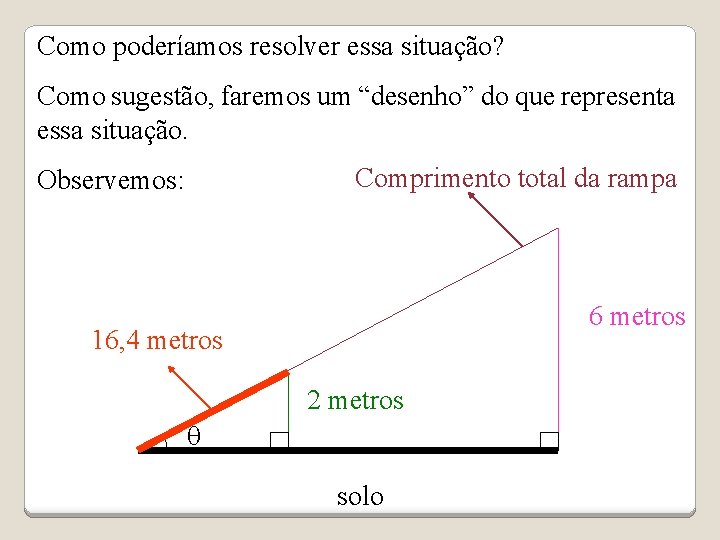
Uma rampa com inclinação constante, (como a que existe em Brasília) tem 6 metros de altura na sua parte mais elevada. Um engenheiro começou a subir, e nota que após ter caminhado 16, 4 metros sobre a rampa está a 2, 0 metros de altura em relação ao solo. Será que este engenheiro somente com esses dados e uma calculadora científica conseguiria determinar o comprimento total dessa rampa e sua inclinação em relação ao solo?

Como poderíamos resolver essa situação? Como sugestão, faremos um “desenho” do que representa essa situação. Comprimento total da rampa Observemos: 6 metros 16, 4 metros 2 metros q solo

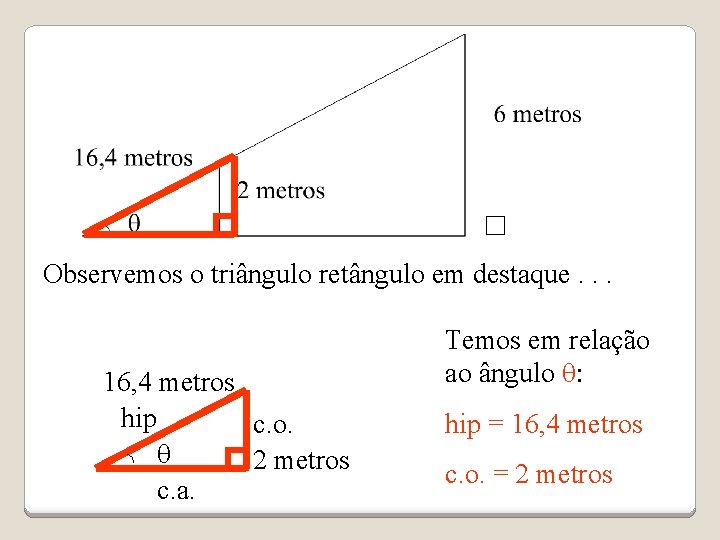
Observemos o triângulo retângulo em destaque. . . 16, 4 metros hip c. o. q 2 metros c. a. Temos em relação ao ângulo q: hip = 16, 4 metros c. o. = 2 metros

Como: hip = 16, 4 metros c. o. = 2 metros 16, 4 metros hip c. o. q 2 metros c. a. Obs. : quando dizemos que arcsen a = 1/2 , podemos transformar essa igualdade em uma pergunta: “qual é o arco, cujo seno vale 1/2? ”, a resposta seria dizer que a = 30°.

Em nosso exercício, chegamos a conclusão que: sen q = 0, 1219512, logo podemos encontrar o ângulo q, com o auxílio da calculadora que normalmente utiliza as funções ASIN ou SIN-1, então, devemos digitar 0, 1219512 e a opção acima de sua calculadora. Se o processo foi realizado corretamente, deverá ser encontrado o valor 7, 00472640907, que iremos considerar como aproximadamente 7°. Encontramos assim, a inclinação da rampa!

Um alpinista muito ágil, percorre um trajeto passando pelos pontos A e B. Não se sabe ao certo o que ocorreu, mas ele conseguiu com o material apropriado chegar a conclusão das medidas abaixo mencionadas. Quando chega até a árvore ele percebe que o único caminho que o levará até o ponto C é escalando -a. (a altura da árvore é representada por h - despreze a largura do tronco) Se sua velocidade média é de 0, 2 m/s, quantos minutos ele demorou para sair do ponto A e chegar ao ponto C? ( )

Solução: Resumidamente, temos o triângulo ao lado que representa nosso desafio.

Igualando o h das equações ( I ) e (II) Como

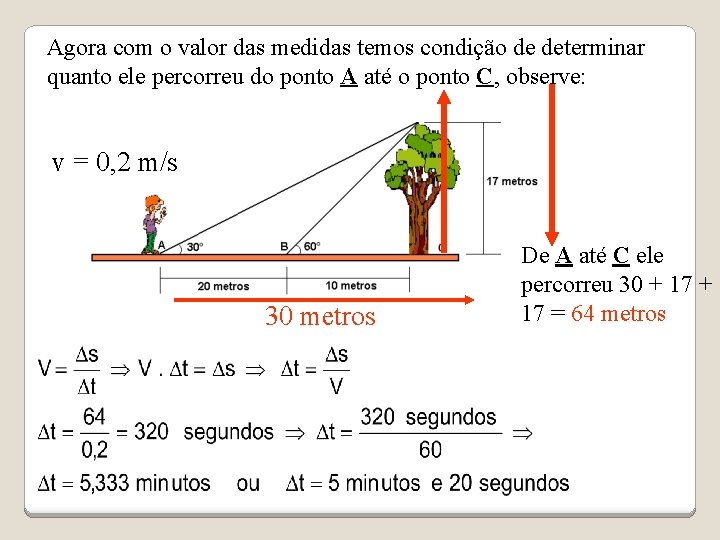
Agora com o valor das medidas temos condição de determinar quanto ele percorreu do ponto A até o ponto C, observe: v = 0, 2 m/s 30 metros De A até C ele percorreu 30 + 17 = 64 metros