Trigonometria e aplicaes A trigonometria possui uma infinidade

Trigonometria e aplicações A trigonometria possui uma infinidade de aplicações práticas. Desde a antiguidade já se usava da trigonometria para obter distâncias impossíveis de serem calculadas por métodos comuns.

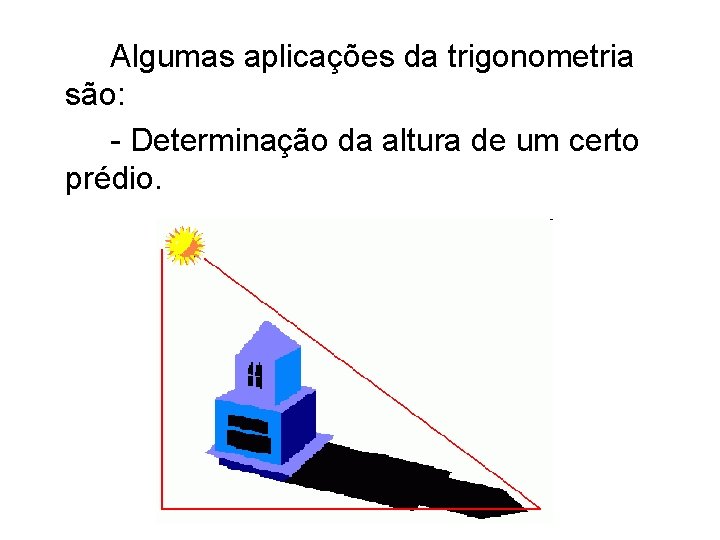
Algumas aplicações da trigonometria são: - Determinação da altura de um certo prédio.

Os gregos determinaram a medida do raio da terra, por um processo muito simples. Um engenheiro precisa saber a largura de um rio para construir uma ponte, o trabalho dele é mais fácil quando ele usa dos recursos trigonométricos. Um cartógrafo (desenhista de mapas) precisa saber a altura de uma montanha, o comprimento de um rio, etc. Sem a trigonometria ele demoraria anos para desenhar um mapa. Tudo isto é possível calcular com o uso da trigonometria do triângulo retângulo.

Triângulo Retângulo É um triângulo que possui um ângulo reto, isto é, um dos seus ângulos mede noventa graus, daí o nome triângulo retângulo. Como a soma das medidas dos ângulos internos de um triângulo é igual a 180°, então os outros dois ângulos medirão 90°.

Observação: Se a soma de dois ângulos mede 90°, estes ângulos são denominados complementares, portanto podemos dizer que o triângulo retângulo possui dois ângulos complementares.

Lados de um triângulo retângulo Os lados de um triângulo retângulo recebem nomes especiais. Estes nomes são dados de acordo com a posição em relação ao ângulo reto. O lado oposto ao ângulo reto é a hipotenusa. Os lados que formam o ângulo reto (adjacentes a ele) são os catetos.

Propriedades do triângulo retângulos: Um triângulo retângulo possui um ângulo reto e dois ângulos agudos complementares. Lados: Um triângulo retângulo é formado por três lados, uma hipotenusa (lado maior) e outros dois lados que são os catetos.

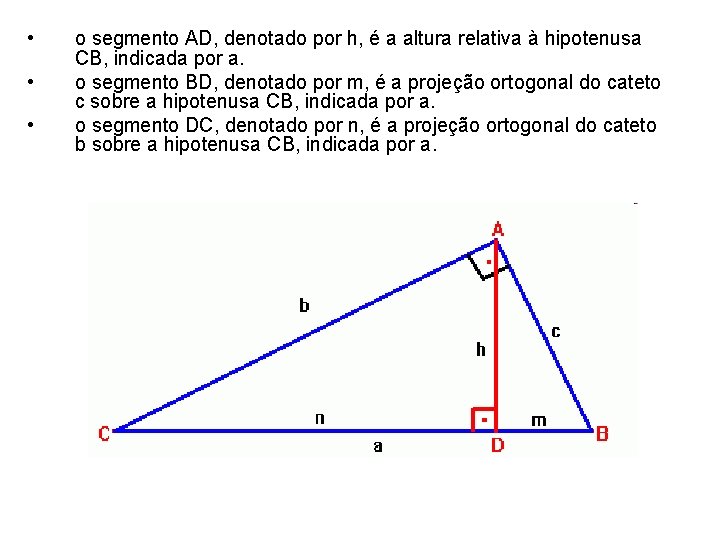
Altura: A altura de um triângulo é um segmento que tem uma extremidade num vértice e a outra extremidade no lado oposto ao vértice, sendo que este segmento é perpendicular ao lado oposto ao vértice. Existem 3 alturas no triângulo retângulo, sendo que duas delas são os catetos. A outra altura (ver gráfico acima) é obtida tomando a base como a hipotenusa, a altura relativa a este lado será o segmento AD, denotado por h e perpendicular à base.

• • • o segmento AD, denotado por h, é a altura relativa à hipotenusa CB, indicada por a. o segmento BD, denotado por m, é a projeção ortogonal do cateto c sobre a hipotenusa CB, indicada por a. o segmento DC, denotado por n, é a projeção ortogonal do cateto b sobre a hipotenusa CB, indicada por a.

Funções trigonométricas básicas As Funções trigonométricas básicas são relações entre as medidas dos lados do triângulo retângulo e seus ângulos. As três funções básicas mais importantes da trigonometria são: seno, cosseno e tangente. O ângulo é indicado pela letra x.

Função Notação sen(x) cosseno cos(x) tangente tan(x) Definição

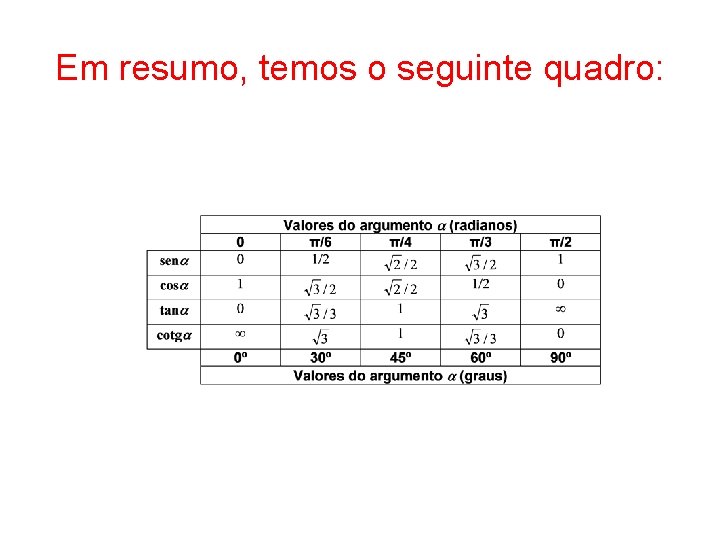
Valores das funções trigonométricas para alguns ângulos-chave Existem alguns ângulos do primeiro quadrante para os quais é possível determinar facilmente os valores tomados pelas funções trigonométricas. Para ângulos de outros quadrantes, torna-se necessário efetuar em primeiro lugar uma redução ao primeiro quadrante.

Em resumo, temos o seguinte quadro:

Exemplos: 1) Um vaivém em órbita terrestre descreve um trajeto tipicamente circular a uma altitude de cerca de 300 km acima da superfície. Sabendo que o raio da Terra é 6380 km, escreva a expressão para a distância do horizonte àquela altitude, e calcule o seu valor.

Solução: Seja R o raio da Terra e h a altitude do vaivém acima da superfície da Terra. Pretende‑se determinar a distância d. O ângulo a é reto porque a reta a que pertence o segmento de comprimento d é perpendicular ao raio da Terra – é tangente à superfície. Aplicando o teorema de Pitágoras, temos:

2)Determine o seno, o cosseno e a tangente do menor ângulo do triângulo retângulo cujos os catetos medem 9 cm e 12 cm.

Resolução: Primeiro usamos o teorema de pitágoras para descobrir o valor da hipotenusa e depois calculamos os valores do seno , cosseno e da tangente.

3) Um avião levanta vôo e sobe fazendo um âmgulo contante de 15º com a horizontal. A que altura estará e qual a distância percorrida, quando alcançar a vertical que passa por uma igreja situada a 2 km do ponto de partida? ( dado: sem 15º = 026 e tg 15º = 0, 27).

Solução O cálculo da altura é feito pela relação da tag de 15º. O cálculo da distância percorrida é feito através do sen 15º.

4) Num triângulo retângulo um cateto mede 15 cm e a hipotenusa 17 cm. Calcule o seno, o cosseno e a tangente do maior ângulo agudo desse triângulo.

Solução: Primeiro aplicamos o teorema de pitágoras para achar o valor do outro cateto. Depois calculamos os valores do seno, cosseno e da tangente.

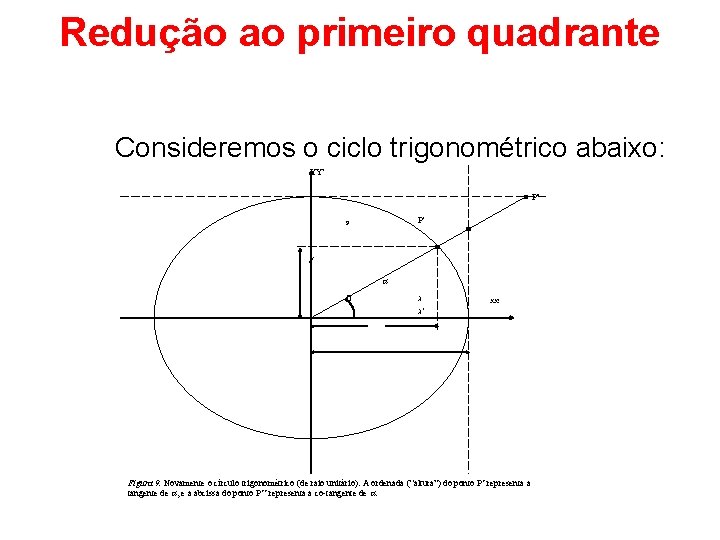
Redução ao primeiro quadrante Consideremos o ciclo trigonométrico abaixo: YY' P' P y a O x XX' x' Figura 9. Novamente o círculo trigonométrico (de raio unitário). A ordenada (“altura”) do ponto P’ representa a tangente de a, e a abcissa do ponto P’’ representa a co tangente de a.

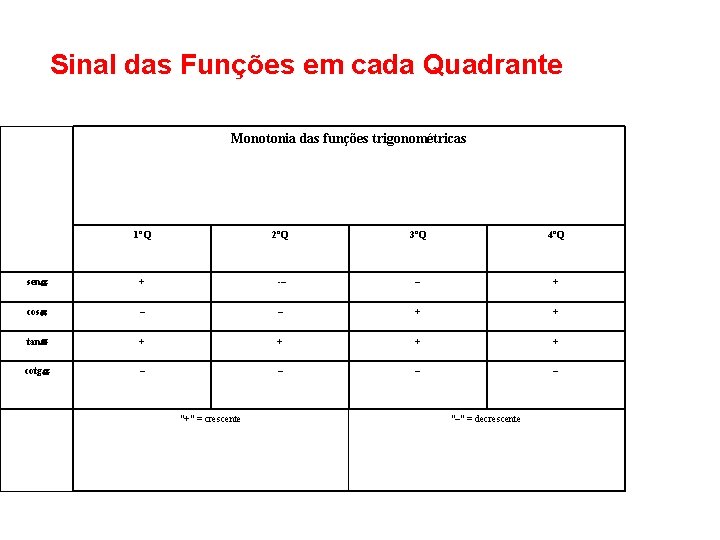
Sinal das Funções em cada Quadrante Monotonia das funções trigonométricas 1ºQ 2ºQ 3ºQ 4ºQ sena + – – + cosa – – + + tana + + cotga – – "+" = crescente "–" = decrescente

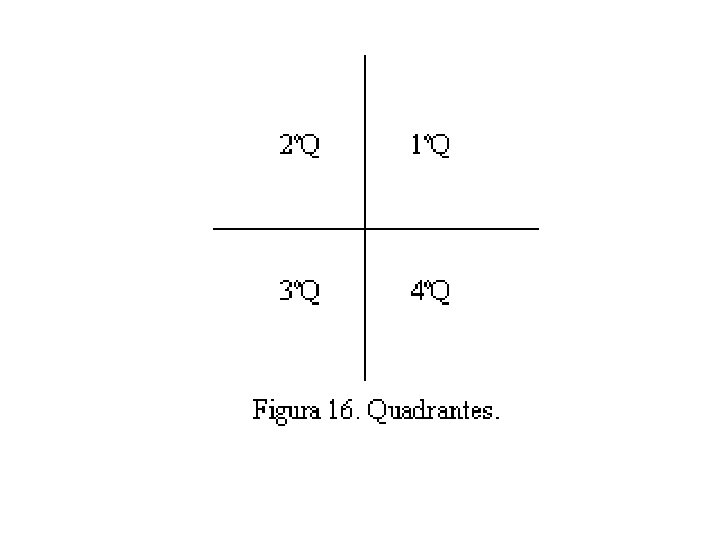
Redução ao primeiro quadrante O círculo trigonométrico é usualmente dividido segundo regiões denominadas quadrantes, como indicado na figura abaixo. São quatro, e indicam-se de acordo com o sentido do crescimento dos ângulos sentido anti-horário.

Assim, iremos descobrir o comportamento das funções trigonométricas nos restantes quadrantes, e compará-lo com os valores tomados pelas funções trigonométricas para ângulos do primeiro quadrante. Na figura vista anteriormente , o 1ºQ corresponde ao intervalo 0 < a < /2, o 2ºQ a /2 < a < , o 3ºQ a < a < 3 /2, e o 4ºQ a 3 /2 < a < 2.

Para fazer a redução do 2º quadrante para o 1º devemos usar a seguinte relação:

Para fazer a redução do 3º quadrante para o 1º devemos usar a seguinte relação:

Para fazer a redução do 4º quadrante para o 1º devemos usar a seguinte relação:

Exercícios: a) b) c) d) e) f) 1) Calcule o seno e o cosseno dos valores abaixo: 210º 150º 330º 240º 1590º 2460º

FIM