FFZS04 Potenciln energie prunost a pevnost hydrostatika a












































































![Viskózní kapaliny II dynamická viskozita (éta) – míra odporu tečení [ ] = kg Viskózní kapaliny II dynamická viskozita (éta) – míra odporu tečení [ ] = kg](https://slidetodoc.com/presentation_image_h2/faeec331e28b0f7e3909fe8dfffb12e8/image-80.jpg)


















- Slides: 102

FFZS-04 Potenciální energie, pružnost a pevnost, hydrostatika a hydrodynamika http: //webak. upce. cz/~stein/lectcz/ffzs_04. html 01. 11. 2010 1

Hlavní body • Gravitace • Gravitační pole v blízkosti Země • Planetární pohyby • Potenciál a potenciální energie • Nauka o pružnosti a pevnosti • Hydrostatika a hydrodynamika • Hydrodynamika krevního oběhu 01. 11. 2010 2

Gravitační pole v blízkosti Země I • Gravitační pole v těsné blízkosti Země lze charakterizovat intenzitou. Její velikost nazýváme gravitačním zrychlením. • Po korekcích gravitačního zrychlení ag = 9. 83 ms-2 na různé vlivy, zvláště rotaci Země, dostáváme měřitelné tíhové zrychlení. Jeho střední hodnota je g = 9. 81 ms-2. 01. 11. 2010 3

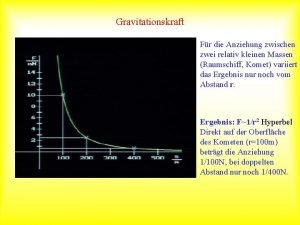
Gravitační pole v blízkosti Země II • Ve vztahu vystupuje součin M. Gravitační konstanta se musí určit z nezávislého měření v laboratoři. Například na torzních vahách. Díky tomu je možné v laboratoři ‘vážit‘ nebeská tělesa. • Tíhové zrychlení vykazuje drobné odchylky v důsledku nepřesně kulového tvaru Země a nehomogenit její hmotnosti a polohy na ní. Toho se využívá při geologickém průzkumu 01. 11. 2010 4

Gravitační pole v blízkosti Země III • Zemi je možné vážit z gravitačního zrychlení nebo z pohybu Měsíce. • Příklad : Určete M a M z a g. 01. 11. 2010 5

Konzervativní pole • Gravitační pole se řadí mezi takzvaná pole konzervativní. • Celková práce potřebná na přenesení hmotnosti po libovolné uzavřené dráze je nulová. • Práce potřebná na přenesení hmotnosti m z bodu A do bodu B nezávisí na cestě, ale jenom na nějaké skalární vlastnosti pole v těchto bodech = potenciálu . W(A->B) = m (B) - m (A) 01. 11. 2010 6

Potenciál I • Je třeba správně chápat rozdíl mezi potenciálem, což je vlastnost pole a potenciální energii, což je vlastnost určitého hmotného tělesa v tomto poli. • Výhody popisu pole pomocí potenciálu : • Skalární • Princip superpozice vede na aritmetické sčítání • Lépe konverguje 01. 11. 2010 7

Potenciál II • Potenciál v jistém bodě centrosymetrického pole získáme rozdělením potenciální energie na vlastnost pole a vlastnost částice: • Potenciál v kalibraci c=0 : 01. 11. 2010 8

Potenciál III • Obecně je pohodlnější popisovat gravitační pole pomocí potenciálu, ale na jeho základě je nutné umět vypočítat intenzitu a sílu : • V centrosymetrickém případě : 01. 11. 2010 9

Gradient I • Gradient skalární funkce je vektor, který má • směr největšího růstu funkce v daném bodě • velikost danou přírustku funkce v jednotkové vzdálenosti od daného bodu v tomto směru : 01. 11. 2010 10

*Gradient II • Gradient je trojrozměrnou obdobou diferenciálu : • Význam gradientu vyplývá z faktu, že skalární součin bude maximální, když jsou jeho činitelé paralelní. 01. 11. 2010 11

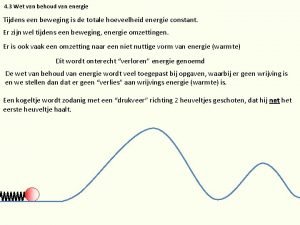
Zákon zachování energie I • Práce dodaná do systému se rovná přírůstku jeho celkové energie, který je roven součtu přírůstku kinetické a přírůstku potenciální energie. • Jak se přírůstky konkrétně rozdělí závisí na dalších podmínkách problému. Je-li práce kladná může se kinetická energie i snížit, ale její pokles musí být vykompenzován odpovídajícím vzrůstem energie potenciální 01. 11. 2010 12

Zákon zachování energie II • Je-li práce dodaná do systému nulová zachovává se celková energie, tedy součet energie kinetické a potenciální. (Zatím uvažujeme jen tyto dva druhy energie). • Jeden druh energie se ale může měnit v druhý. • V těsné blízkosti Země : 01. 11. 2010 13

Pohyb satelitů I • Obecně se tělesa otáčejí kolem společného těžiště. • Je-li satelit podstatně lehčí než centrální těleso lze společné těžiště ztotožnit s těžištěm centrálního tělesa. • Uvažujme pro jednoduchost kruhovou dráhu. V prvním přiblížení je dostředivá síla realizována silou gravitační a platí : 01. 11. 2010 14

Pohyb satelitů II • Můžeme například vyjádřit rychlost oběhu : • Nyní chápeme 3. Keplerův zákon pro satelity obíhající stejné centrální těleso: 01. 11. 2010 15

Pohyb satelitů III • Jsou-li hmotnosti těles srovnatelné, musí se uvažovat pohyb kolem jejich společného těžiště. Čili dochází i k pohybu centrálního tělesa. • Takto lze vysvětlit příliv a odliv nebo odhalit exoplanety u vzdálených hvězd. • Používá se přímého pozorování a moderněji spektroskopických metod (136). 01. 11. 2010 16

*1. Kosmická rychlost • 1. Kosmická rychlost je rychlost oběhu těsně u povrchu vesmírného tělesa. • Tedy zakřivení dráhy vodorovného vrhu akorát kopíruje povrch tělesa. • Takový pohyb je možný pouze, když těleso nemá atmosféru, jinak je zbržděno (a shoří). • V případě Země se jedná o hodnotu fiktivní : 01. 11. 2010 17

*2. Kosmická rychlost • 2. Kosmická neboli úniková rychlost je taková, při které má těleso kinetickou energii dostatečnou k tomu, aby se dostalo z dosahu Země do nekonečna • Opět nesmí dojít ke ztrátám průletem atmosférou • Rozdíl od rychlosti potřebné k dosažení např. Měsíce je ale nepatrný. 01. 11. 2010 18

*3. Kosmická rychlost • 3. Kosmická neboli úniková rychlost je taková, při které má těleso kinetickou energii dostatečnou k tomu, aby se dostalo ze Země z dosahu Slunce do nekonečna • Úniková rychlost z oběžné dráhy Země je • Ms je hmotnost Slunce, rsz je poloměr dráhy Země. • Při vypuštění sondy ve směru obíhání Země lze ale odečíst obvodovou rychlost Země, tedy cca 30 km/s. 01. 11. 2010 19

*Proč shořela Columbie I • Celková energie satelitu : • Kde jsme použili dříve odvozený vztah pro rychlost satelitu: 01. 11. 2010 20

*Proč shořela Columbie II • Podle předchozího se celková energie satelitu musí zvětšit dodáme-li práci. Přitom : • se zvětší její vzdálenost • její rychlost se zmenší(!) • Když naopak satelit vstupuje do atmosféry a je bržděn atmosférou nebo svými motory, klesá jeho výška, ale roste rychlost. Musí tedy (v určité fázi letu, například než může letět jako letadlo nebo být bržděno padáky) vydržet obrovské teploty. 01. 11. 2010 21

*Moderní teorie gravitace • Albert Einstein se zabýval ekvivalencí gravitační a setrvačné hmotnosti na ní a na předpokladu, že fyzikální zákony musí v každé (i neinerciální) soustavě být stejné vybudoval obecnou teorii relativity. • Podle ní hmotnost zakřivuje časoprostor ve svém okolí. • Experimentálními potvrzeními této teorie jsou například ohyb elektromagnetických vln v blízkosti velkých těles (Slunce, Jupiter) a stáčení roviny oběhu Merkura. 01. 11. 2010 22

Atomová hypotéza I • Richard Feynman – jeden z největších fyziků 20. století a autor výborné a nadčasové učebnice “Feynmanovy kurzy fyziky“ – tvrdí, že pokud bychom směli zanechat budoucím generacím jedinou větu, měla by znít : Svět je složen z atomů, malých částic, které jsou v neustálém pohybu, když se přiblíží, přitahují se, ale když se přiblíží ještě více, naopak se odpuzují. • Rozměry atomů se měří v (SI) zakázaných, ale velice praktických jednotkách - angströmech 1Ǻ = 10 -10 m 01. 11. 2010 23

Atomová hypotéza II • Kdybychom zvětšili jablko na rozměr Země (asi 108 krát), atomy by měly rozměr jablka. 6. 10 -2. 108 m = 6. 106 m ~ 6 Ǻ. 108 = ~ 6. 10 -10. 108 m = ~ 6 cm Je zajímavé, že i při tomto zvětšení : by atomové jádro nebylo vidět pouhým okem. Mělo by totiž průměr jen řádově jednotky m ! poloměr Země by nedosáhl k nejbližší hvězdě. Musel by se ještě 60 krát vynásobit! 01. 11. 2010 24

Dalekodosahové síly I Cherchez le puits (de potential) • Součástky hmoty - atomy nebo molekuly na sebe vzájemně působí dalekodosahovými silami, které mají následující vlastnosti: • na velké vzdálenosti jsou zanedbatelné • při menších vzdálenostech jsou přitažlivé • při ještě menších vzdálenostech jsou odpudivé • existuje alespoň jedna rovnovážná vzdálenost, v níž se přitažlivé a odpudivé síly kompenzují 01. 11. 2010 25

Dalekodosahové síly II • Dalekodosahové síly lze zjednodušeně vystihnout průběhem potenciální energie částice, která se blíží k částici, umístěné do počátku – tzv. potenciálovou jámou. • v blízkosti minima ji lze aproximovat parabolou • lze pomocí ní kvalitativně vysvětlit například: • • 01. 11. 2010 existenci a pravidelnost kondenzovaného stavu elastické chování látek teplotní roztažnost mechanické vlastnosti sedlin 26

Pružnost I • Z vzájemného působení součástek hmoty, které jsme si přiblížili pomocí potenciálové jámy, je patrné, že tělesa nemohou být dokonale tuhá. Jejich tvar v každé situaci odpovídá jisté rovnováze vnějších a vnitřních sil. • Změnou působení vnějších sil se mění síly uvnitř. Snaží se vyrovnat účinek této změny. Výsledkem je nová rovnováha odpovídající stavu napjatosti. 01. 11. 2010 27

Pružnost II • Vzájemné působení může být velmi složité a existují látky s bizardními vlastnostmi. • Naše potenciálová jáma je zjednodušení, zhruba fungující pro velké množství látek. • Zatím přijměme tvrzení, že při velmi malých deformacích se při vymizení vnějších sil, vrátí i těleso do původní rovnováhy. • Zaveďme si vhodně veličiny, které jsou ve hře: 01. 11. 2010 28

Napětí I • Experiment ukazuje, že pro deformační účinek je rozhodující veličinou působící síla, vztažená na jednotku plochy, na kterou působí tzv. mechanické napětí • Jednotkou napětí je 1 Pascal [Pa]=Nm-2 01. 11. 2010 29

Napětí II • Odezva látek může být komplikovaná, ale i u nejjednodušších látek (homogenních a izotropních) je rozdílná nejméně v tečném a normálovém směru. Proto má význam rozkládat napětí alespoň na normálové a tečné: 01. 11. 2010 30

Deformace • Odezva látek je vždy úměrná rozměru před deformací, proto je užitečné ji k tomuto původním rozměru vztáhnout. Podle typu deformace používáme například relativní • prodloužení • • Střih dx dy • stlačení 01. 11. 2010 v 31

Závislost napětí na deformaci • Průběh namáhání látek se obvykle (ale ne vždy) zobrazuje jako závislost napětí na deformaci. Má následující oblasti a meze: • úměrnosti. . . zde platí Hookův zákon • elasticity. . . návrat do původního tvaru • plasticity. . . zůstává trvalá deformace • kluzu. . . velká změna chování • pevnosti. . . porušení materiálu 01. 11. 2010 32

Závislost napětí na deformaci oblast tečení elastická oblast mez pevnosti plastická oblast proporcionality – zde platí Hookův zákon 01. 11. 2010 33

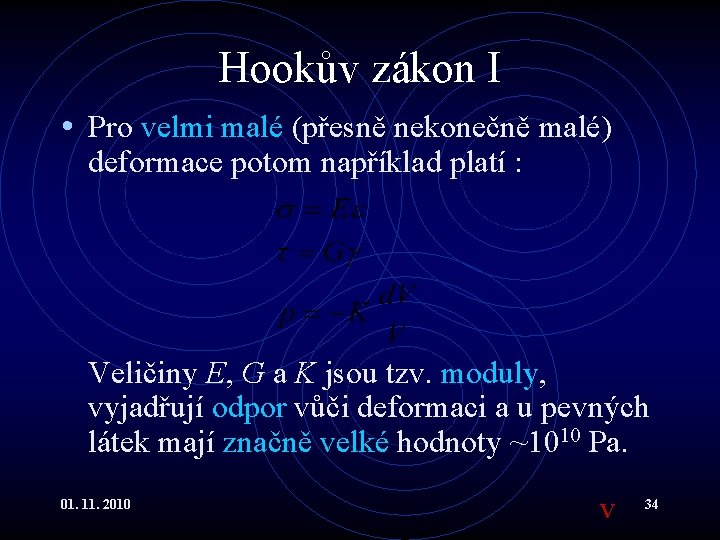
Hookův zákon I • Pro velmi malé (přesně nekonečně malé) deformace potom například platí : Veličiny E, G a K jsou tzv. moduly, vyjadřují odpor vůči deformaci a u pevných látek mají značně velké hodnoty ~1010 Pa. 01. 11. 2010 v 34

Hookův zákon II • Moduly se nazývají : • E …Youngův modul pružnosti v podélném prodloužení • G … Youngův modul pružnosti ve smyku • K … modul objemové pružnosti • Často se používají i reciproké hodnoty modulů. Vyjadřují samozřejmě poddajnost (compliance) materiálů a jsou typicky velmi malé. 01. 11. 2010 35

Hookův zákon III • Mezi ději ve směru namáhání a ve směru kolmém existuje souvislost. Například protahujeme-li drát, dochází v kolmém směru ke zužování. Popisujeme jej relativním příčným zkrácením, které je úměrné normálovému napětí : • Míru změny v příčném směru popisujeme novým materiálovým parametrem Poissonovým číslem (ný) nebo (jeho reciprokou) Poissonovou konstantou m : 01. 11. 2010 36

Hookův zákon IV • Podélný a příčný rozměr po deformaci lze vyjádřit : • Budeme-li krychli V = aaa namáhat hydrostatickým tlakem p = n, projeví se ve změně k každého rozměru i příčné vlivy a objem po deformaci bude : 01. 11. 2010 37

Hookův zákon V • Čili po zanedbání kvadratických a vyšších členů můžeme vyjádřit relativní změnu objemu: • a srovnáním dostáváme součinitel objemové stlačitelnosti γ nebo modul objemové pružnosti K : 01. 11. 2010 38

*Hookův zákon VI • Poissonova konstanta nebo Poissonovo číslo se také uplatní ve vztahu mezi modulem ve smyku a v tahu, takže jednoduché materiály lze charakterizovat jen dvěma materiálovými parametry : 01. 11. 2010 39

*Deformace neizotropních látek I • V obecném případě neizotropních těles je nutné napětí i deformaci vyjádřit pomocí symetrických tenzorů druhého řádu a . • ij je j-tá složka napětí působící na plošku kolmou k ose i. • pq je výchylka plošky kolmé k ose p ve směru osy q. 01. 11. 2010 40

*Deformace neizotropních látek II • Zobecněný Hookův zákon je možné vyjádřit jako: ij = Cijpq pq • Cijpq je obecně 36 nezávislých elastických parametrů. • Každá symetrie materiálu znamená i symetrií v C, tedy nějakou vzájemnou relaci, čili i snížení počtu nezávislých materiálových parametrů. • Nejtriviálnější je symetrie vůči záměně dvojic ij a pq. Ta snižuje počet nezávislých parametrů na 21. Tento počet odpovídá monokrystalům v triklinické soustavě. • Amorfní nebo polykrystalické látky se chovají jako izotropní a zůstávají u nich jen dva parametry E a G. 01. 11. 2010 41

Úvod do mechaniky tekutin I • Tekutiny je společný název pro kapaliny a plyny. Přitažlivé síly v nich jsou kohézního charakteru. • Mají společný téměř nulový modul ve smyku. Díky tomu snadno mění tvar. • Relativně lehce se rozdělují. • Na rozdíl od plynů jsou kapaliny téměř nestlačitelné. • V případě, že se neprojevují efekty, které souvisí s existencí atomové struktury, lze tekutiny, podobně jako pevné látky považovat za tak zvané kontinuum – spojité prostředí. 01. 11. 2010 42

Tekutiny II • Z hlediska elastických vlastností lze tekutiny definovat následovně: • kapaliny. . . K velmi veliké, G malé • plyny. . . K konečné dané EOS, G malé 01. 11. 2010 43

Tekutiny III • Pro odhalení základních mechanických vlastností kapalin a plynů je vhodné začít od ideální kapaliny a později zavádět korekce, popisující reálnější chování například viskozitu a stlačitelnost. • Ideální kapalina má K nekonečné a G nulové. Čili ideální kapalina je nestlačitelná, ale neexistují v ní smyková napětí ani deformace. 01. 11. 2010 44

Hydrostatika ideální kapaliny I • Hydrostatika se zabývá kapalinami nebo plyny v rovnováze, bez ohledu na to, jak a za jak dlouho k ní dojde (např. smůla na stromě není v rovnováze). • Budeme nejprve uvažovat ideální a tedy dokonale nestlačitelnou kapalinu, navíc homogenní a izotropní. • Je pohodlné charakterizovat kapalinu fyzikálními veličinami vztaženými na jednotku objemu, tedy hustotami fyzikálních veličin. 01. 11. 2010 45

Hydrostatika ideální kapaliny II • Nejběžnější jsou : • hustota je hmotnost na jednotku objemu : = m/V, [ ] = kg m-3 • hustota působících sil , tedy síla na jednotku objemu : , [f] = N m-3 • tlak p lze chápat jako hustotu tlakové energie : [p] = N/m 2 = J/m 3 01. 11. 2010 46

*Základní rovnice hydrostatiky I • Pro tenzor napětí u ideální kapaliny platí jednoduše Pascalův zákon : ij=-p ij. ij je tzv. Croneckerovo delta. Nabývá dvou hodnot: ij=1 pro i=j nebo ij=0 pro i j. • p = F/S [Pa] je tlak - normálové napětí. • Budeme upravovat základní vztah pro rovnováhu kontinua : 01. 11. 2010 47

*Základní rovnice hydrostatiky II • Po dosazení za tenzor napětí platí : • Síla působí ve směru největší změny tlaku nebo naopak největší změna tlaku je ve směru působící síly. • Jde-li speciálně o sílu vytvořenou polem majícím potenciál 01. 11. 2010 48

*Základní rovnice hydrostatiky III • Tedy: • A konečně po integraci obdržíme : • Tuto rovnici lze iterpretovat tak, že místa stejného tlaku leží na ekvipotenciálních plochách a s poklesem potenciálu = růstem hloubky se tlak zvětšuje. 01. 11. 2010 49

Základní rovnice hydrostatiky IV • Všechna rozhraní kapalin, samozřejmě včetně hladiny, která je rozhraním kapaliny a plynu, jsou tedy ekvipotenciální plochy. • Hladiny nejsou ve skutečnosti zcela vodorovné : • kopírují například zemský povrch a sledují i jemnější změny potenciálu v důsledku rotace Země, její nehomogenity i společné působení Měsíce a Slunce. • také se zakřivují v blízkosti okrajů nádoby. 01. 11. 2010 50

Tlak v kapalině I Pascalův zákon • V důsledku neexistence tečných napětí působí v každém bodě pouze tlak (=normálové napětí) a je stejný ze všech směrů. • Na tomto principu je založena např. hydraulika. Můžeme-li zanedbat vlastní tíhu kapaliny, je tlak v ní všude stejný a na různě velké plochy tedy působí různě velká síla: F 1/S 1 = p 2 = F 2/S 2 01. 11. 2010 51

Tlak v kapalině II • Předpokládejme • gravitační pole v blízkosti povrchu Země. = gz • svislá osa je z, její kladná část míří vzhůru. • Obecně musíme připustit závislost hustoty na z, potom : 01. 11. 2010 52

Tlak v kapalině III Průběh tlaku v kapalině je lineární • U těžko stlačitelných kapalin lze hustotu považovat za konstantní a tedy : • Integrace vede na lineární pokles tlaku s výškou : • Často uvažujeme naopak vzrůst s hloubkou pod hladinou: 01. 11. 2010 53

Tlak v kapalině IV Průběh tlaku v atmosféře je exponenciální • Předpokládejme izotermickou atmosféru, stlačitelnou podle Boyle-Marriotova zákona • Potom : • Diferenciální rovnici řešíme integrací po separaci proměnných a po odlogaritmování: 01. 11. 2010 54

Archimédův zákon I • Těleso ponořené do tekutiny je nadlehčováno silou, která se rovná tíze tekutiny tělesem vytlačené. • Nadlehčování je způsobeno tlakovými silami, které se snaží tekutinu “vrátit”, do míst, odkud byla tělesem vytlačena nebo kam se může alespoň principiálně dostat. • Protože tlak roste s hloubkou, lze očekávat, že výslednice sil bude směřovat vzhůru. 01. 11. 2010 55

Archimédův zákon II • Archimédův zákon • úzce souvisí s růstem tlaku s hloubkou • lze ilustrovat na tělese speciálního tvaru nebo • dokázat obecně jako rovnováhu objemových a povrchových sil. Druhý důkaz nepožaduje konstantní hustotu, čili nezávisí na možné stlačitelnosti tekutiny a platí tedy i pro plyny a také tělesa, která mohou být v několika prostředích, např. neúplně ponořená. 01. 11. 2010 56

Archimédův zákon III • Mějme rotační válec o výšce h a podstavě S v ideální kapalině o hustotě 0. • Tlakové síly na plášť se v každé hloubce vyrovnají. • Nevykompenzovaná zůstane pouze tlaková síla působící na spodní podstavu a tedy vzhůru, protože tato podstava je hlouběji o výšku válce než podstava horní: F = Sh 0 g. • To je ale přesně tíha vytlačené kapaliny. 01. 11. 2010 57

Archimédův zákon IV • V kapalině, která je v rovnováze si mysleme její určitý objem libovolného tvaru. • Tento objem má svoji hmotnost, a tíha směřuje svisle dolů. • Na povrch objemu působí tlakové síly. Protože je objem v rovnováze, musí jejich výslednice vykompenzovat tíhu, čili musí směřovat svisle vzhůru a její velikost se musí rovnat tíze myšleného objemu. 01. 11. 2010 58

Povrchové napětí I • Částice kapaliny blízko rozhraní mají ve svém okolí prostředí dvojího druhu. To obecně vede k nesymetrii působících sil, jak dovedeme vysvětlit opět pomocí potenciálové jámy. • Takový efekt existuje i na rozhraní dvou pevných látek. Jak jsme poznali, rozhraní kapaliny se vyznačuje tím, že zaujímá v každém bodě směr kolmo k působící síle. 01. 11. 2010 59

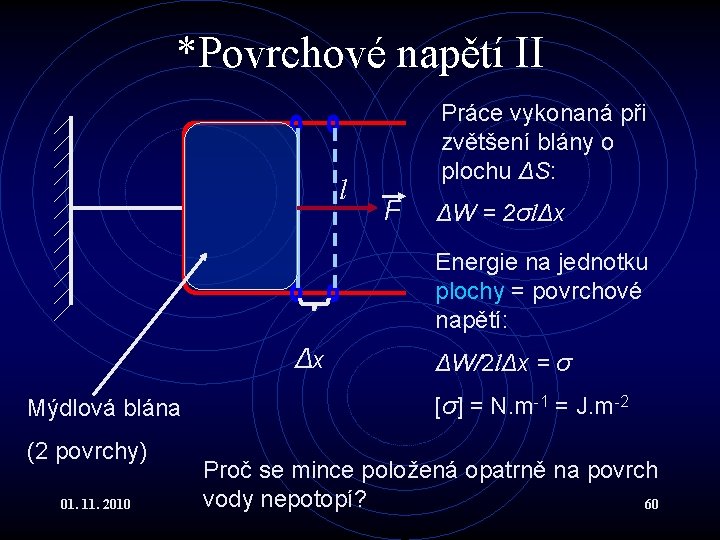
*Povrchové napětí II l Práce vykonaná při zvětšení blány o plochu ΔS: F ΔW = 2σlΔx Energie na jednotku plochy = povrchové napětí: Δx Mýdlová blána (2 povrchy) 01. 11. 2010 ΔW/2 lΔx = σ [σ] = N. m-1 = J. m-2 Proč se mince položená opatrně na povrch vody nepotopí? 60

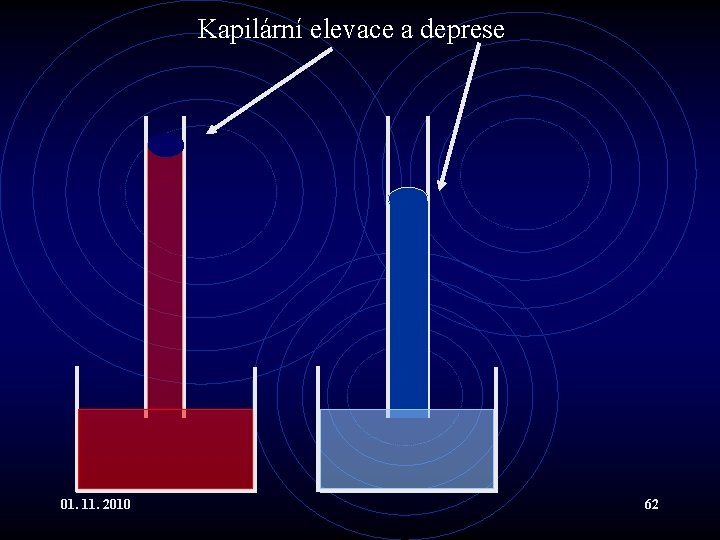
Povrchové napětí III • Například na rozhraní kapalina – plyn působí síly směřující do kapaliny. • Výsledkem je, že se rozhraní snaží zaujímat minimální povrch, např. se tvoří kapky. • Na rozhraní kapalina – pevná látka mohou síly směřovat : • do kapaliny - kapalina látku nesmáčí • z kapaliny ven - kapalina látku smáčí. 01. 11. 2010 61

Kapilární elevace a deprese 01. 11. 2010 62

Úvod do hydrodynamiky • Popsat tekutiny v pohybu patří mezi nejobtížnější problémy, které v klasické fyzice existují. • Pro jednoduchost vyjdeme ze zákonů zachování, které platí pro pomalé proudění neviskózní a nestlačitelné kapaliny. • Později podrobněji popíšeme chování nejjednodušší viskózní, tzv. Newtonovské kapaliny a ukážeme příklady chování některých ne -Newtonovských kapalin. 01. 11. 2010 63

Hydrokinematika I • Proudící kapalinu lze popsat pomocí : • Trajektorií, křivek, po nichž se částice pohybují v čase. Částicí se zde rozumí makroskopicky malý ale mikroskopicky velký objem kapaliny. • Proudnic, křivek tečných v každém bodě k vektorům rychlosti. Proudnice tvoří proudové trubice, jejichž stěnami kapalina neprochází. Jejich vnitřek se nazývá proudová vlákna. 01. 11. 2010 64

Zákony zachování • U ideálních kapalin lze jednoduše využít zákonů zachování. Zachovávají se : • Množství – rovnice kontinuity • Hybnost • Energie – Bernoulliho rovnice 01. 11. 2010 65

Rovnice kontinuity • Časový objemový průtok Q kapaliny určitou proudovou trubicí se zachovává. Jinak by se kapalina musela někde objevovat nebo mizet. • Má-li proudová trubice u nestlačitelné kapaliny v jednom místě průřez S 1 a v druhém S 2, platí : S 1 v 1 = Q 2 = S 2 v 2 • U stlačitelných tekutin je konstantní průtok hmotnostní a platí : S 1 v 1 1 = S 2 v 2 2 01. 11. 2010 66

Zachování hybnosti • Ke změně směru proudové trubice může dojít jen v případě existuje-li impuls síly, který příslušnou změnu hybnosti umožní v čase : • Proudnice musí zpravidla podpírat i síly tlakové, změna rychlosti vede k nové rovnováze. 01. 11. 2010 67

Zachování energie • Bernoulliho rovnice vyjadřuje zákon zachování hustoty energie : • V praxi se vyjadřuje několika způsoby, například v rozměrech délkových : 01. 11. 2010 68

*Odvození Bernoulliho rovnice I • Uvažujme dvě různá místa, ohraničující určitý úsek jedné proudové trubice, která jsou popsána rychlostí vi, tlakem pi a výškou hi. • Působením tlakových sil se určitý objem V se přemístí za čas t z prvního místa do druhého. • Na objemy působí z vnějšku úseku tlakové síly opačné orientace Fi = Si pi. • Práce, kterou vykonají tyto síly za t se musí rovnat přírůstku celkové energie daného objemu. 01. 11. 2010 69

*Odvození Bernoulliho rovnice II • Tedy : • Po dosazení : • Aplikujme rovnici kontinuity : 01. 11. 2010 70

Odvození Bernoulliho rovnice III • Tento vztah, vyjadřující zachování energie, bývá zvykem vztáhnout ke jednotkovému objemu, tedy vydělit V a přeskupit podle uvažovaných míst : • Rci odvodil Švýcar Daniel Bernoulli 1700 -1783 • Celková energie proudící kapaliny má tedy tři složky : tlakovou, kinetickou a potenciální. 01. 11. 2010 71

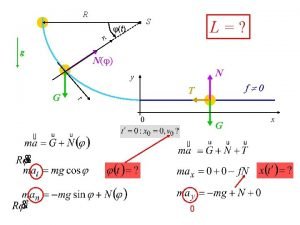
Použití Bernoulliho rovnice I • Bernoulliho rovnice lze použít jako prvního přiblížení při řešení řady praktických problémů. • Uvažujme například výtok kapaliny ze široké (nebo doplňované) nádoby malým otvorem umístěným v hloubce h pod hladinou. V Bernoulliho rovnici můžeme udělat několik úprav a zanedbání : 01. 11. 2010 72

Použití Bernoulliho rovnice II • Oba tlaky jsou atmosférické : p 1= p 2. • Vyjádříme hloubku: h = z 1 – z 2 • Rychlost v 1 můžeme zanedbat. • Po zkrácení a úpravě : Je zajímavé, že tento tzv. Torrichellio vzorec byl znám již sto let před Bernoullim. 01. 11. 2010 73

*Použití Bernoulliho rovnice III • Není-li možné rychlost v 1 zanedbat, použijeme rovnici kontinuity v 1 = v 2 S 2/S 1 : • Po zkrácení , zavedení hloubky a úpravě : (výraz má zjevně smysl jen pro S 1 > S 2) 01. 11. 2010 74

Použití Bernoulliho rovnice IV • Uvažujeme-li místa o stejné výšce je z Bernoulliho rovnice patrná zajímavá vlastnost proudících tekutin a to, že v místech s větší rychlostí je nižší tlak. Na tomto principu je založena řada jevů od bouchání dveří v průvanu, přes střílení rohového kopu ve fotbale, po létání letadel. Protože jsou důsledky na první pohled překvapivé, je tento jev znám jako hydrodynamický paradoxon. • Významné je jeho využití při měření rychlosti. 01. 11. 2010 75

*Použití Bernoulliho rovnice V • Pitotova trubice (fajfka) : • do měřené kapaliny jsou vnořeny dvě trubice, ústí jedné je kolmo, ústí druhé rovnoběžně s jejím proudem (fajfka) v 2 = 0. • v každé trubici vystoupí kapalina do výšky zi podle odpovídající tlaku pi = gzi při jejím ústí • ve vztahu vystupuje pouze rozdíl výšek zi 01. 11. 2010 76

*Použití Bernoulliho rovnice VI • Venturiho trubice (potřebuje zúžení) : • do měřené kapaliny jsou kolmo vnořeny dvě trubice, jedna v místě s průřezem S 1, druhá S 2. • v každé trubici vystoupí kapalina do výšky zi podle odpovídající tlaku pi = gzi při jejím ústí 01. 11. 2010 77

*Použití Bernoulliho rovnice VII • Z obou rovnic : • Pro rychlost v 1 a průtok Q platí po úpravě : 01. 11. 2010 78

Viskózní kapaliny I • Při proudění reálných tekutin se sousední vrstvy ovlivňují tečným napětím, které závisí na vzájemné rychlosti vrstev a viskozitě tekutiny. • Mějme tekutinu proudící ve směru osy x. Potom pro tečné napětí, čili napětí působící ve směru proudění, platí Newtonův zákon: 01. 11. 2010 79
![Viskózní kapaliny II dynamická viskozita éta míra odporu tečení kg Viskózní kapaliny II dynamická viskozita (éta) – míra odporu tečení [ ] = kg](https://slidetodoc.com/presentation_image_h2/faeec331e28b0f7e3909fe8dfffb12e8/image-80.jpg)
Viskózní kapaliny II dynamická viskozita (éta) – míra odporu tečení [ ] = kg m-1 s-1 = Nm-2 s = Pa s Starší jednotka Poise [P]=gcm-1 s-1=0. 1 Pa s Převrácená hodnota se nazývá tekutost: = 1/ • Často se používá viskozita vztažená na hustotu, tzv. kinematická viskozita (ný) = / • D je gradient rychlosti rovný časové změně deformace ve střihu. • • 01. 11. 2010 80

Viskózní kapaliny III • Dynamická a kinematická viskozita některých kapalin: • • • ETOH benzín rtuť olej voda 01. 11. 2010 [Pa s] 1. 2 10 -3 2. 9 10 -4 1. 5 10 -3 0. 26 1. 005 10 -3 (ný) [m 2/s] 1. 51 10 -6 4. 27 10 -7 1. 16 10 -7 2. 79 10 -4 0. 804 10 -6 81

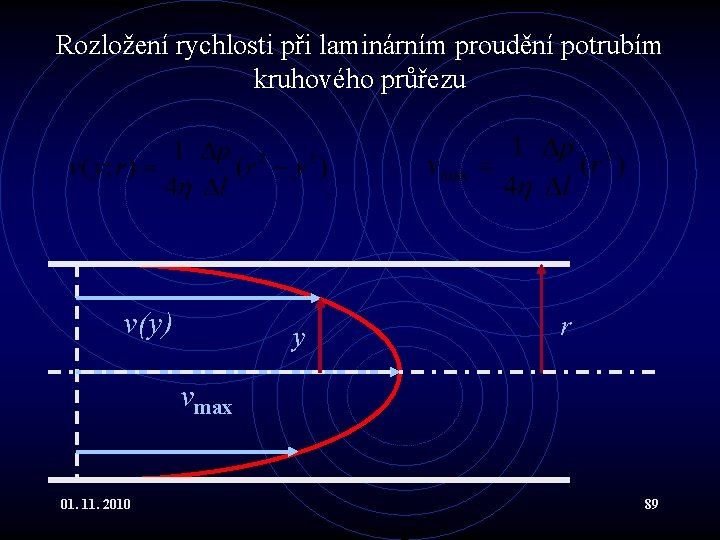
Viskózní kapaliny IV • Viskozita : • snižuje průtok kapaliny (za daných podmínek) • způsobuje, že rychlost v protékaném průřezu není konstantní, ale má určité rozložení, u krajů je minimální (nulová) a uprostřed maximální. • Ukážeme, že v (proudové) trubici kruhového průřezu je rozložení rychlosti na vzdálenosti od osy parabolické. 01. 11. 2010 82

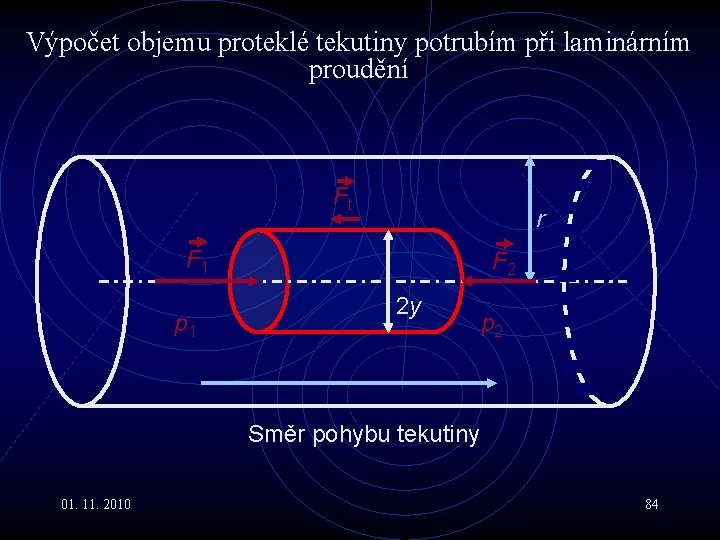
*Viskózní kapaliny V • Mysleme si v laminárně a rovnoměrně proudící kapalině váleček o poloměru y. Na • podstavy působí tlakové síly (p 1 > 0, p 2 < 0) • plášť síla způsobená třením okolních vrstev. • Pohybuje-li se válec rovnoměrně, musí být všechny síly na něj působící, tedy síly působící na podstavy plus na plášť v rovnováze : 01. 11. 2010 83

Výpočet objemu proteklé tekutiny potrubím při laminárním proudění Ft r F 1 p 1 F 2 2 y p 2 Směr pohybu tekutiny 01. 11. 2010 84

*Viskózní kapaliny VI • Předpokládejme, že p 1 > p 2 a tedy kapalina se pohybuje ve směru růstu souřadnice x. • Znaménko + znamená, že třecí sílu bychom považovali (jako obvykle) za kladnou, kdyby měla směr rychlosti. • Protože první člen je kladný, musí být třecí síla záporná, čili brzdící a rychlost klesá směrem od osy. 01. 11. 2010 85

*Viskózní kapaliny VII • Po zavedení p = p 1 – p 2 a úpravě : • Po integraci : 01. 11. 2010 86

*Viskózní kapaliny VIII • Uvažujeme-li trubici o poloměru r. Obdržíme hodnotu integrační konstanty k z okrajové podmínky v(r) = 0 : • a celkově dostáváme parabolickou závislost : 01. 11. 2010 87

*Viskózní kapaliny IX • Důležitou a snadněji měřitelnou veličinou je průtok. Celkový průřez musíme rozdělit na mezikruží o poloměru y, v nichž je vždy rychlost konstantní: • Celkový průtok obdržíme integrací : • To je známá Hagen-Poiseuillova rovnice. 01. 11. 2010 88

Rozložení rychlosti při laminárním proudění potrubím kruhového průřezu v(y) y r vmax 01. 11. 2010 89

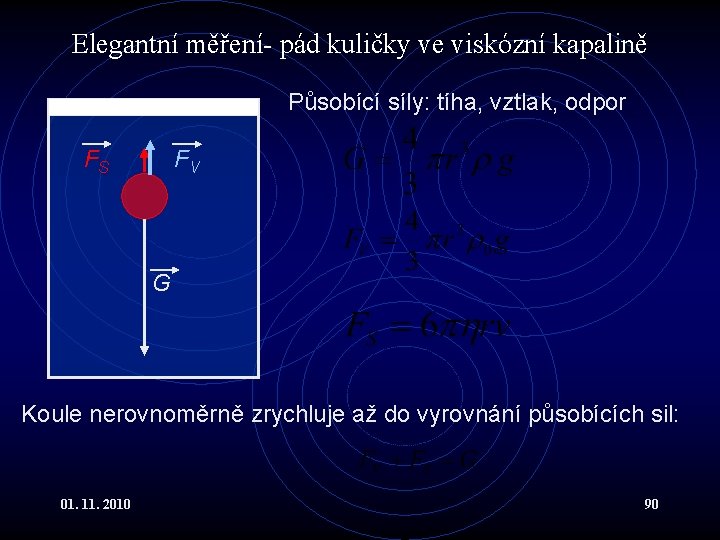
Elegantní měření- pád kuličky ve viskózní kapalině Působící síly: tíha, vztlak, odpor FS FV G Koule nerovnoměrně zrychluje až do vyrovnání působících sil: 01. 11. 2010 90

Viskózní kapaliny X • Stokesův zákon: • Na kuličku o poloměru r, která se pohybuje malou rychlostí v v kapalině působí brzdící síla F = 6 rv • Kulička o hustotě bude po ustálení rovnováhy padat v kapalině 0 konstantní rychlostí vt : 01. 11. 2010 91

Viskózní kapaliny XI • Laminární proudění • brzdící síla je úměrná rychlosti • rychlost je úměrná r 2 • střední rychlost vyplývající z H-P rovnice <v>=Qv/S je také úměrná r 2 a tlakovému spádu • Za mezí Stokesova zákona : • Často je brzdící síla úměrná v 2 : Fd = Cd. Sv 2 • Cd je parametr, který závisí na tvaru 01. 11. 2010 92

Viskózní kapaliny XII • Pro posouzení, zda je proudění ještě laminární se používá tzv. Reynoldsovo číslo. • pro kuličku o poloměru r, pohybující se rychlostí v • pro kapalinu pohybující se střední rychlostí <v> v trubici o poloměru r platí : • Pro R >1000 se považuje proudění za turbulentní (ve jmenovateli posledního výrazu je řecké (ný), tedy kinematická viskozita!) 01. 11. 2010 93

Dynamika krevního oběhu I Na základě práce Dr. J. Tulky • Krevní oběh je udržován srdcem. Levá část síň -> komora pumpuje krev do velkého (tělního) oběhu a pravá část do malého oběhu (plic). • Krev v aortě : • <v> = 0. 3 ms-1 • r = 0. 01 m • = 1060 kg m-3 • = 3. 3 10 -3 Pa s • R 970 proudění je těsně ještě laminární. 01. 11. 2010 94

Dynamika krevního oběhu II • Ve velkých žilách proudí krev pomaleji, jen rychlostí <v> = 0. 1 ms-1 a ve vlásečnicích dokonce jen rychlostí <v> = 0. 001 ms-1. Pomocí rovnice kontinuity můžeme odhadnout, že celkový průřez • velkých žil je 3 krát větší než průřez aorty • vlásečnic je 300 krát větší než průřez aorty 01. 11. 2010 95

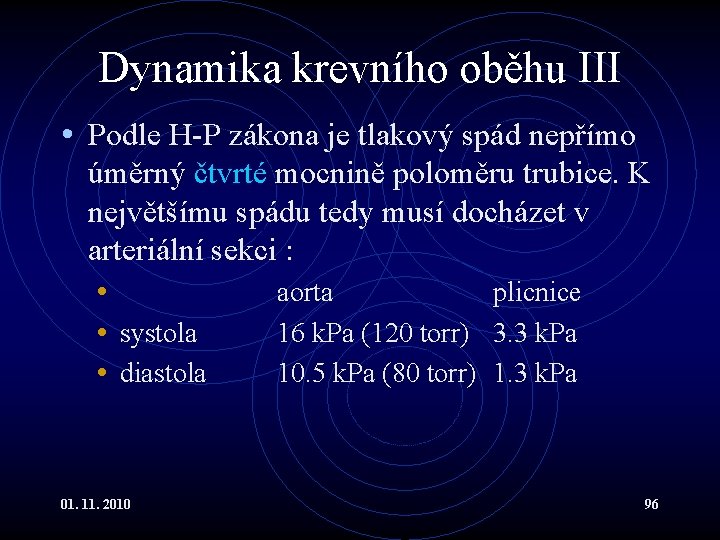
Dynamika krevního oběhu III • Podle H-P zákona je tlakový spád nepřímo úměrný čtvrté mocnině poloměru trubice. K největšímu spádu tedy musí docházet v arteriální sekci : • aorta plicnice • systola 16 k. Pa (120 torr) 3. 3 k. Pa • diastola 10. 5 k. Pa (80 torr) 1. 3 k. Pa 01. 11. 2010 96

Dynamika krevního oběhu IV • Práce srdce bývá vyjadřována jako součet • statické – objemové dodávající tlakovou energii • kinetické – dodávající kinetickou energii odpovídající příslušné střední rychlosti : • Pro střední hodnoty V = 70 ml a p = 13. 3 k. Pa je WS= 0. 93 J a WK = 0. 003 J, tedy W = 0. 94 J 01. 11. 2010 97

Dynamika krevního oběhu V • Práce pravé komory je asi jedna pětina práce komory levé. Celková mechanická práce srdce při jedné systole je tedy asi 1. 13 J. • Při tepové frekvenci 70 min-1 je výkon srdce přibližně 1. 3 W. • Tato hodnota představuje jen asi jednu desetinu celkového mechanického výkonu srdce. Převažující část se spotřebuje na udržování stálého napětí (tonusu) srdeční svaloviny. 01. 11. 2010 98

Dynamika krevního oběhu VI • Celkový srdeční výkon je tedy 13 W, což představuje přibližně 13% celkového klidového výkonu organismu. • Srdce ale funguje nepřetržitě řadu let. Za 60 let života vykoná práci 2. 5 GJ, což je : • 3 s výkonu Chvaletické elektrárny • Vyzdvižení 30 t břemene na Mt. Everest 01. 11. 2010 99

Příklad - potenciál I • Spočítejme práci, kterou musíme (jako vnější činitel) dodat pro přemístění hmotnosti m z r. A do r. B v centrálním poli jisté hmotnosti M. • Závisí jen na vzdálenostech od tělesa a práci musíme dodávat jen při zvětšování r, protože působíme proti přitažlivé síle. 01. 11. 2010 100

Příklad - potenciál II Tuto práci chápeme jako přírůstek potenciální energie srovnáním 01. 11. 2010 101

Příklad - potenciál III • Práce dodaná tělesu vnějším činitelem zvýší jeho potenciální energii. Tu obecně definujeme včetně integrační konstanty c, dané kalibrací: • Často předpokládáme, že potenciální energie v nekonečnu je nulová, což odpovídá c=0 : 01. 11. 2010 ^ 102
 Smyková pevnost zemin
Smyková pevnost zemin Potentielle energie in elektrische energie
Potentielle energie in elektrische energie Hydrostatický tlak test
Hydrostatický tlak test Pascalov zakon
Pascalov zakon Voorbeelden van chemische energie
Voorbeelden van chemische energie Entalpie definitie
Entalpie definitie Fotoelectric
Fotoelectric Energie potentielle electrostatique
Energie potentielle electrostatique Vnitřní energie tělesa prezentace
Vnitřní energie tělesa prezentace Zoomasa
Zoomasa Chaine d'information et d'énergie portail automatique
Chaine d'information et d'énergie portail automatique Willem buiter energie
Willem buiter energie Energie gaat nooit verloren
Energie gaat nooit verloren Kernfusion iter
Kernfusion iter Potenciální energie
Potenciální energie Energie mécanique
Energie mécanique Mappa concettuale centrale idroelettrica
Mappa concettuale centrale idroelettrica Mechanická energie
Mechanická energie Sos energie
Sos energie Potential energy summary
Potential energy summary Kinetická energie
Kinetická energie Tp l'inégale répartition de l'énergie solaire sur terre
Tp l'inégale répartition de l'énergie solaire sur terre Potenciální energie
Potenciální energie Vzorec polohové energie
Vzorec polohové energie Energie grootheid
Energie grootheid Lampiris document reprise energie
Lampiris document reprise energie K jake premene energie dochazi v elektromotoru
K jake premene energie dochazi v elektromotoru Mechanická energie
Mechanická energie Chapitre 3 l'énergie et ses manifestations
Chapitre 3 l'énergie et ses manifestations Potenciální energie
Potenciální energie Pal waarden tabel
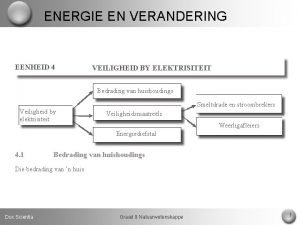
Pal waarden tabel Veiligheid van elektrisiteit
Veiligheid van elektrisiteit Mechanická energie
Mechanická energie Avantaje energia eoliana
Avantaje energia eoliana Polohová energie pružnosti
Polohová energie pružnosti Energieaufwertung
Energieaufwertung Uhlk
Uhlk Chaine d'information et d'énergie portail automatique
Chaine d'information et d'énergie portail automatique Kinetische rotationsenergie
Kinetische rotationsenergie Unitate de masura energie mecanica
Unitate de masura energie mecanica Mechanická energie
Mechanická energie Energie pool schweiz
Energie pool schweiz énergie rayonnante exemple
énergie rayonnante exemple énergie renouvelables et non renouvelables
énergie renouvelables et non renouvelables Martien visser energie
Martien visser energie Casa independenta energetic
Casa independenta energetic Energie activation
Energie activation Wta gesuch
Wta gesuch Hladiny potenciálnej energie
Hladiny potenciálnej energie Fluchtgeschwindigkeit definition
Fluchtgeschwindigkeit definition énergie de liaison d'un noyau
énergie de liaison d'un noyau Foto elektrisch effect
Foto elektrisch effect Kogelwiel
Kogelwiel Jiný název pro polohovou energii
Jiný název pro polohovou energii Gibbsova energia
Gibbsova energia Formule reactiewarmte
Formule reactiewarmte Instalatie folosita pentru producerea vaporilor
Instalatie folosita pentru producerea vaporilor Rijn en ijssel energie
Rijn en ijssel energie Vakuumenergie dunkle energie
Vakuumenergie dunkle energie Energie potentielle ressort
Energie potentielle ressort Mechanická energie
Mechanická energie Kinetická energie
Kinetická energie Innere energie teilchenmodell
Innere energie teilchenmodell Sodexo energie et maintenance
Sodexo energie et maintenance Chaine d'information et d'énergie portail automatique
Chaine d'information et d'énergie portail automatique Bande d'énergie
Bande d'énergie Principiul minimului de energie
Principiul minimului de energie Energie
Energie Les sources d'énergie non renouvelable
Les sources d'énergie non renouvelable Konzervativní síla
Konzervativní síla Ren energie
Ren energie Biomasa este considerata o sursa importanta de energie
Biomasa este considerata o sursa importanta de energie Wet van behoud van gedoe
Wet van behoud van gedoe Normaal krag definisie
Normaal krag definisie Mechanická energie
Mechanická energie Kinetická energie
Kinetická energie Kinetická energia telesa závisí od
Kinetická energia telesa závisí od Značka pohybové energie
Značka pohybové energie Rozvod elektrickej energie
Rozvod elektrickej energie Energie solaire algerie
Energie solaire algerie Energie gaat nooit verloren
Energie gaat nooit verloren Gezeitenradius
Gezeitenradius L'énergie emmagasinée dans un condensateur
L'énergie emmagasinée dans un condensateur Netradičné zdroje energie
Netradičné zdroje energie Iischi energie
Iischi energie Innere energie
Innere energie Alternativní zdroje energie prezentace
Alternativní zdroje energie prezentace Dunkle materie
Dunkle materie Innere energie
Innere energie Energie thermique
Energie thermique énergie de liaison d'un noyau
énergie de liaison d'un noyau Tok energie
Tok energie Potentiele energie veer
Potentiele energie veer Moc definicja
Moc definicja Parabole solaire stirling
Parabole solaire stirling Energia ce
Energia ce Rozvod elektrickej energie
Rozvod elektrickej energie Examples of kinetic energy
Examples of kinetic energy Netradičné zdroje energie
Netradičné zdroje energie Pluritechnologique
Pluritechnologique