Chapitre 3 2 Lnergie potentielle lastique dun ressort













- Slides: 22

Chapitre 3. 2 –L’énergie potentielle élastique d’un ressort idéal ISMAIL A

Préambule : travail et force variable Travail pour un déplacement le long de l’axe des X : W = Fx Dx, où Fx est la composante de la force F le long du déplacement Dx.

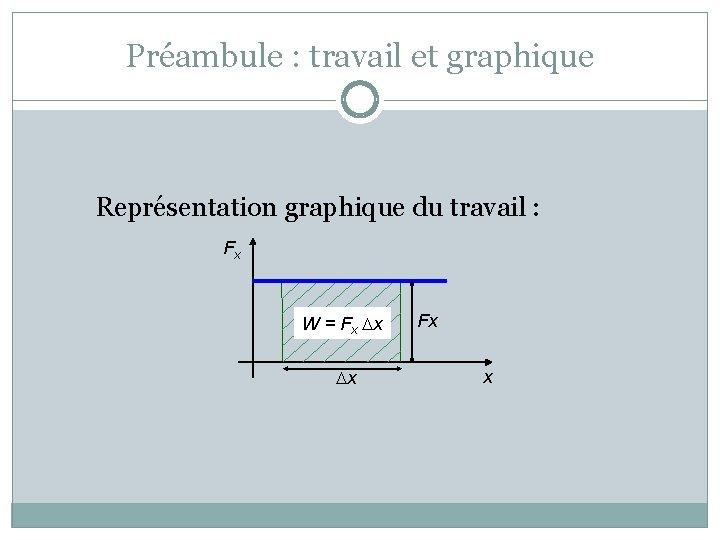
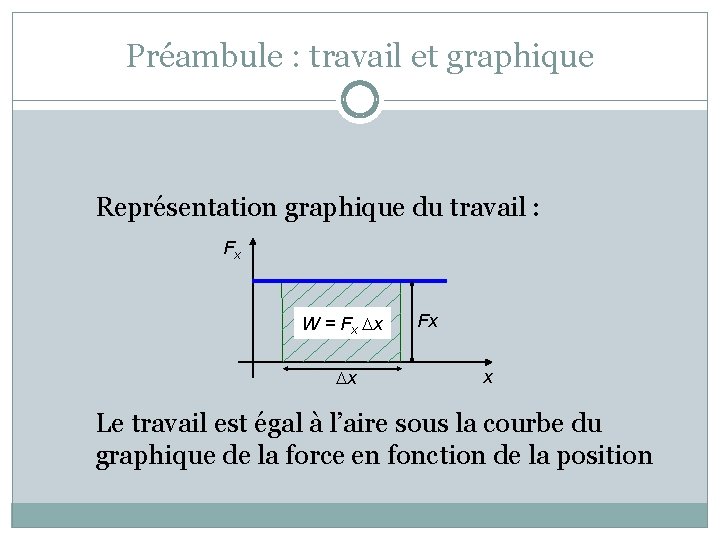
Préambule : travail et graphique Représentation graphique du travail : Fx W = Fx Dx Dx Fx x

Préambule : travail et graphique Représentation graphique du travail : Fx W = Fx Dx Dx Fx x Le travail est égal à l’aire sous la courbe du graphique de la force en fonction de la position

Préambule : Travail et force variable Fx x

Préambule : Travail et force variable Fx x

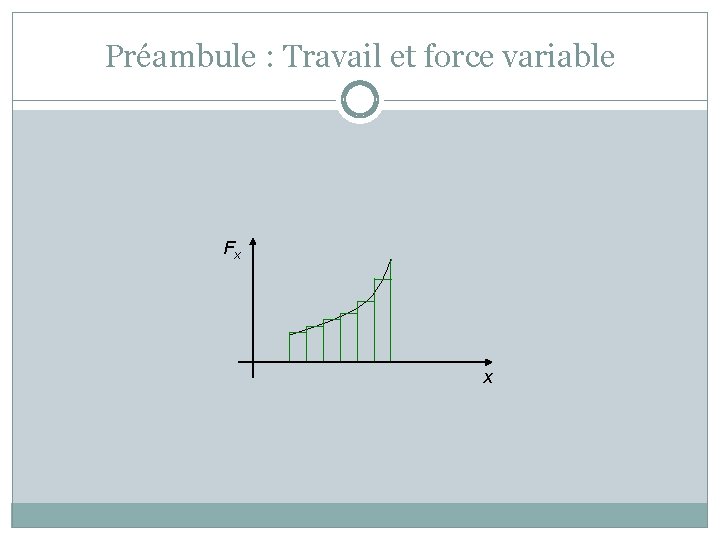
Préambule : Travail et force variable Fx x

Préambule : Travail et force variable Si la force est variable, la courbe est plus complexe, mais le résultat est le même : le travail est l’aire sous la courbe du graphique de la force en fonction de la position

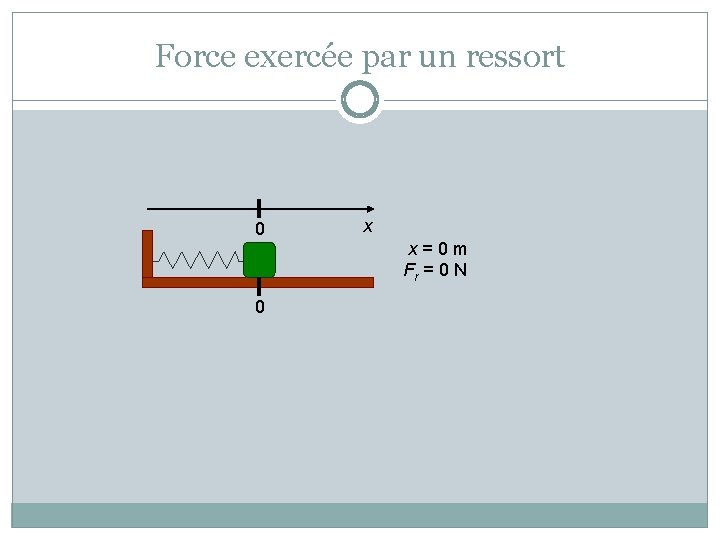
Force exercée par un ressort 0 0 x x=0 m Fr = 0 N

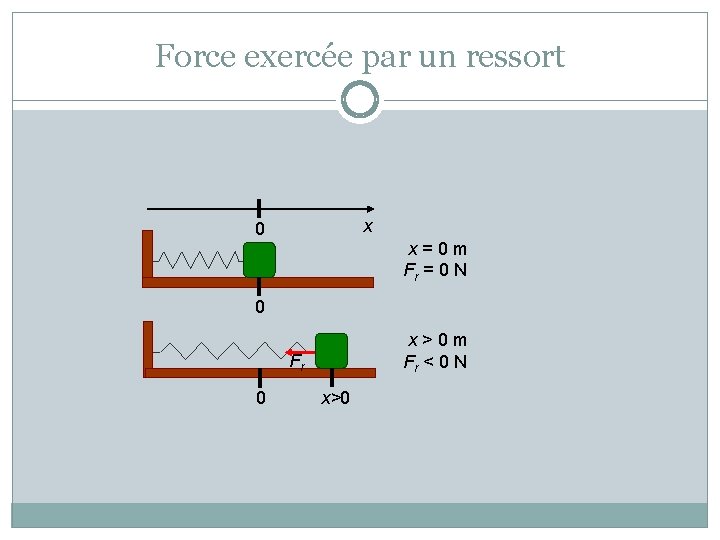
Force exercée par un ressort x 0 x=0 m Fr = 0 N 0 x>0 m Fr < 0 N Fr 0 x>0

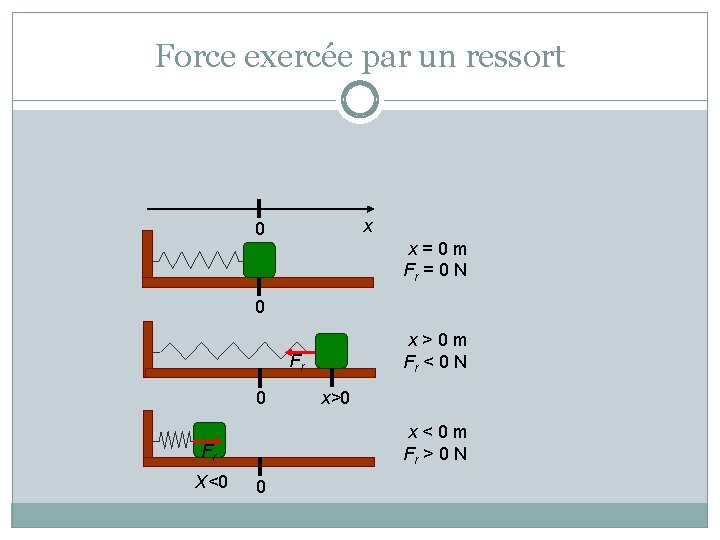
Force exercée par un ressort x 0 x=0 m Fr = 0 N 0 x>0 m Fr < 0 N Fr 0 x<0 m Fr > 0 N Fr X<0 x>0 0

Force exercée par un ressort la force exercée par un ressort est donnée par Fx = - k x où Fx : Force du ressort de l’axe x (N) k : Constante de rappel du ressort (N/m) x : Étirement du ressort (m)

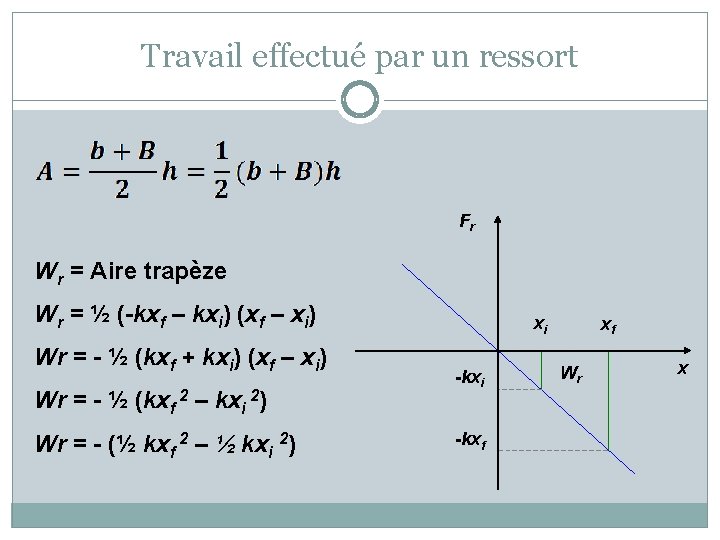
Travail effectué par un ressort Fr Wr = Aire trapèze Wr = ½ (-kxf – kxi) (xf – xi) Wr = - ½ (kxf + kxi) (xf – xi) Wr = - ½ (kxf 2 – kxi 2) Wr = - (½ kxf 2 – ½ kxi 2) xi -kxf xf Wr x

Remarque Wr = - (½ kxf 2 – ½ kxi 2) Le travail effectué par le ressort ne dépend pas de la trajectoire, mais il ne dépend que de la différence de position entre xi et xf.

L’énergie potentielle d’un objet est son énergie en vertu de sa position. C’est en quelque sorte de l’énergie emmagasinée qui pourra être tranformée en énergie cinétique (mouvement de l’objet)

Énergie potentielle du ressort À partir du travail effectué par un ressort : Wr = - (½ kxf 2 – ½ kxi 2) Nous allons associer une énergie emmagasinée dans le ressort pour son étirement initial et une énergie emmagasinée dans le ressort pour son étirement final. Ce type d’énergie porte le nom d’énergie potentielle : Urf = ½ kxf 2 et Uri = ½ kxi 2

Énergie potentielle du ressort Ainsi on peut obtenir l’énergie potentielle du ressort : Wr = - (Urf – Uri) = - Dur De façon générale, on peut associer l’énergie potentielle que le ressort peut donner à un système en fonction de sa compression ou de son étirement : Ur = ½ ke 2

Énergie cinétique et énergie potentielle D’après le théorème de l’énergie cinétique : Kf = Ki + Wtot Dans le cas où la seule force exercée sur un objet est celle d’un ressort, alors : K f = K i + Wr Kf = Ki – (Urf – Uri) Kf + Urf = Ki + Uri

Un petit problème. . . Un bloc de 0, 3 kg et de vitesse initiale nulle est accroché à une extrémité d’un ressort idéal dont l’autre extrémité est fixe. La constante de rappel vaut 40 N/m. Le ressort est initialement maintenu comprimé de 20 cm alors qu’on lâche le tout. (Le bloc est soutenu par une surface horizontale sans frottement) Déterminez le module de la vitesse du bloc alors que le ressort est étiré de 10 cm. Faites votre choix : (a) 0, 6 m/s (b) 2, 0 m/s (c) 3, 7 m/s

Une petite réponse … Un bloc de 0, 3 kg et de vitesse initiale nulle est accroché à une extrémité d’un ressort idéal dont l’autre extrémité est fixe. La constante de rappel vaut 40 N/m. Le ressort est initialement maintenu comprimé de 20 cm alors qu’on lâche le tout. (Le bloc est soutenu par une surface horizontale sans frottement) Déterminez le module de la vitesse du bloc alors que le ressort est étiré de 10 cm. Réponse : (a) 0, 6 m/s (b) 2, 0 m/s (c) 3, 7 m/s

Solution Évaluons les énergies : Données : Avec la conservation de l’énergie:

Solution(suite) Remarque : La vitesse calculée n’est pas vectorielle, mais c’est le module. v = 2 m/s
 Energie potentielle ressort
Energie potentielle ressort Petit pays chapitre 1
Petit pays chapitre 1 Tirez pas sur le scarabée fiche de lecture
Tirez pas sur le scarabée fiche de lecture Le petit prince chapitre 1
Le petit prince chapitre 1 Le petit prince chapitre 24
Le petit prince chapitre 24 Erste kosmische geschwindigkeit
Erste kosmische geschwindigkeit Raideur ressort flexion
Raideur ressort flexion Energie potentielle electrostatique
Energie potentielle electrostatique Konsumentenhed
Konsumentenhed Ableitung kinetische energie
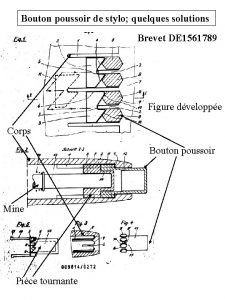
Ableitung kinetische energie Mecanisme stylo ressort
Mecanisme stylo ressort Pouteau colles
Pouteau colles Det potentielle marked
Det potentielle marked Ressort pour pante
Ressort pour pante Tpmep
Tpmep Gerard marchant fracture
Gerard marchant fracture Dun and bradstreet delinquency predictor score
Dun and bradstreet delinquency predictor score Nota sesi bilgisi
Nota sesi bilgisi Adun batu pahat
Adun batu pahat Black that symbolizes roughness and fierceness
Black that symbolizes roughness and fierceness Fonction dusage dun pont
Fonction dusage dun pont Kawasan peta negeri sembilan
Kawasan peta negeri sembilan Nota değerleri
Nota değerleri