ESTADSTICA DEPARTAMENTO DE MATEMTICA APLICADA 1 TEMA 1

ESTADÍSTICA DEPARTAMENTO DE MATEMÁTICA APLICADA 1

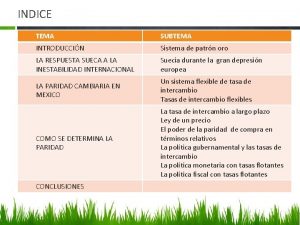
TEMA 1: ESTADÍSTICA DESCRIPTIVA 1. 1 CONCEPTOS GENERALES. 1. 2 DISTRIBUCIÓN DE FRECUENCIAS. 1. 3 REPRESENTACIONES GRÁFICAS. 1. 4 MEDIDAS DE TENDENCIA CENTRAL. 1. 5 MEDIDAS DE DISPERSIÓN. 1. 6 MEDIDAS DE ASIMETRÍA. 1. 7 EL MODELO DE REGRESIÓN SIMPLE. PRÁCTICAS 1. ESTADÍSTICA DESCRIPTIVA. 2. MODELOS DE REGRESIÓN. 2

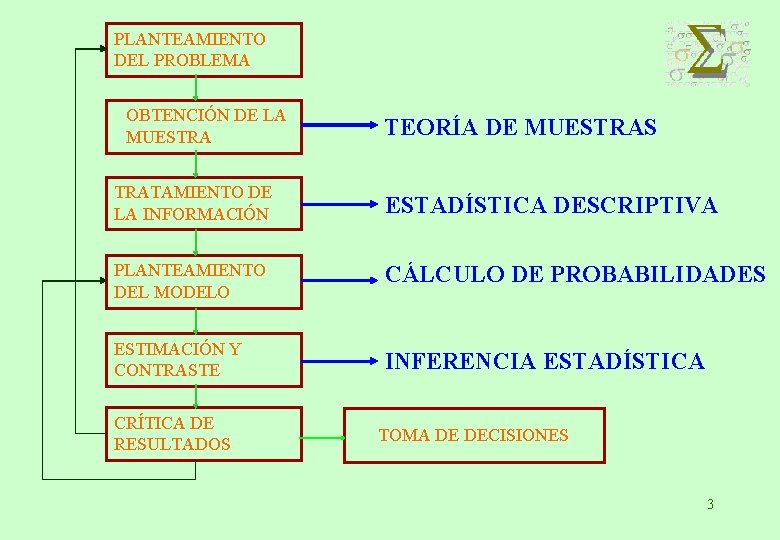
PLANTEAMIENTO DEL PROBLEMA OBTENCIÓN DE LA MUESTRA TEORÍA DE MUESTRAS TRATAMIENTO DE LA INFORMACIÓN ESTADÍSTICA DESCRIPTIVA PLANTEAMIENTO DEL MODELO CÁLCULO DE PROBABILIDADES ESTIMACIÓN Y CONTRASTE INFERENCIA ESTADÍSTICA CRÍTICA DE RESULTADOS TOMA DE DECISIONES 3

ESTADÍSTICA DESCRIPTIVA TRATA DE DESCRIBIR CONJUNTOS DE DATOS RESUMIENDO LA INFORMACIÓN QUE ESTOS PROPORCIONAN, UTILIZANDO: • TABLAS DE FRECUENCIAS • TÉCNICAS GRÁFICAS • TÉCNICAS ANALÍTICAS: MEDIDAS DE POSICIÓN, DISPERSIÓN Y FORMA 4

CONCEPTOS FUNDAMENTALES • POBLACIÓN: conjunto de elementos o individuos de los que interesa estudiar alguna característica. • MUESTRA: subconjunto de elementos de una población. RAZONES PARA ESTUDIAR UNA MUESTRA • Coste • Tiempo • Personal cualificado • Procesos destructivos 5

• Llamamos CARÁCTER a la cualidad objeto de nuestro estudio. caracteres pueden ser: Los • Cuantitativos: la característica toma valores numéricos (número de peticiones a un servidor, tiempo entre peticiones consecutivas, etc) • Cualitativos: la característica no toma valores numéricos (sexo, color de pelo, etc) • Los caracteres cuantitativos se llaman VARIABLES ESTADÍSTICAS. Los caracteres cualitativos se llaman VARIABLES CUALITATIVAS. • Las variables estadísticas pueden ser de dos tipos: • Discretas: Discretas si la característica toma valores aislados (finitos o infinito numerable). • Continuas: Continuas si toma cualquier valor de uno o varios intervalos. 6

1. 2 DISTRIBUCIÓN DE FRECUENCIAS Sea una muestra de tamaño n; supongamos que X toma como valores distintos x 1, x 2 , . . . , xk. • FRECUENCIA ABSOLUTA DE xi: Es el número, ni , de veces que se repite xi. • FRECUENCIA RELATIVA DE xi: es el cociente entre la frecuencia absoluta y n. • FRECUENCIA ABSOLUTA(RELATIVA) ACUMULADA DE xi. Si llamamos x*1, x*2 , . . . , x*k a los valores ordenados de menor a mayor: Frecuencia absoluta acumulada de x*i Frecuencia relativa acumulada de x*i 7

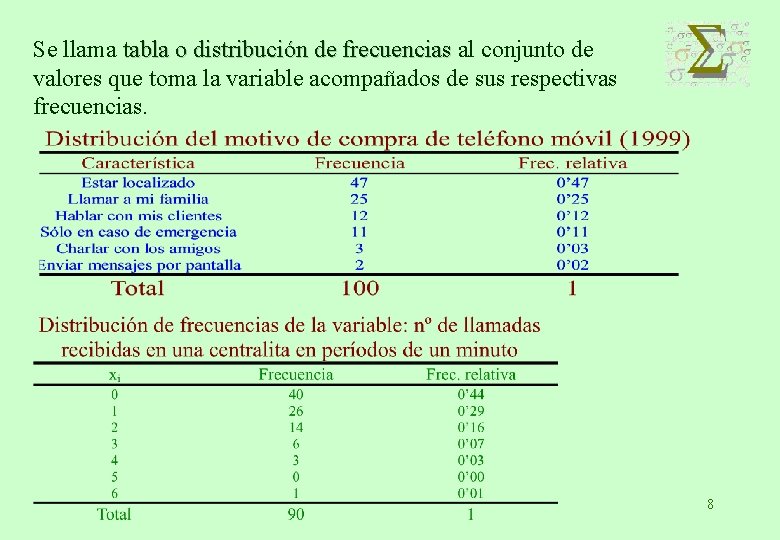
Se llama tabla o distribución de frecuencias al conjunto de valores que toma la variable acompañados de sus respectivas frecuencias. 8

• Estas tablas son útiles para resumir la información de una variable cuando: • El estudio está basado en pocas observaciones, a lo sumo 20 • El estudio está basado en muchas observaciones de una variable que toma pocos valores distintos, a lo sumo 20. • Si el número de valores distintos que toma la variable es grande (mayor que 20), se agrupan los datos en intervalos para construir la tabla de frecuencias. • Llamaremos a estas variables VARIABLES AGRUPADAS. Al resto nos referiremos como VARIABLES NO AGRUPADAS o sin agrupar. 9

VARIABLES AGRUPADAS EN INTERVALOS A estos intervalos se les llama intervalos de clase. Al punto medio de cada clase se le denomina marca de clase. El número de intervalos de clase lo determina la persona que está realizando el estudio, aunque una posibilidad razonable es tomar el entero más próximo a 1+3. 3 log 10(n). Si los valores que toma la variable están repartidos de manera homogénea, todos los intervalos se toman con la misma amplitud; en otro caso se tomarán intervalos de amplitud variable, procurando que no queden intervalos con menos del 5% de los datos ni con más del 30%. 10

Los datos siguientes corresponden al consumo mensual de litros de leche de 40 familias: N=40, 1+3’ 3 log 40=6’ 29, luego tomamos 6 intervalos. Como R=103’ 3 -10=93’ 3 y 93’ 3: 6=15’ 55, podemos tomar 6 intervalos de amplitud 16 repartiendo el exceso (2’ 7) entre el primer intervalo y el último. De este modo la agrupación en intervalos quedaría: Como podemos observar hay intervalos con menos del 5% de los datos y con más del 30%, por lo que habría que optar por una agrupación en intervalos de amplitud variable. 11

Una posible agrupación en intervalos de amplitud variable es la siguiente: Como puede observarse todos los intervalos contienen más del 5% y menos del 30% de los datos. 12

1. 3 MÉTODOS GRÁFICOS • VARIABLES CUANTITATIVAS: ¨Diagrama de barras ¨Histograma ¨Polígono de frecuencias ¨Diagrama de caja o box-plot ¨Diagrama de sectores • VARIABLES CUALITATIVAS: ¨Diagrama de rectángulos ¨Diagrama de sectores • OTRAS REPRESENTACIONES. 13

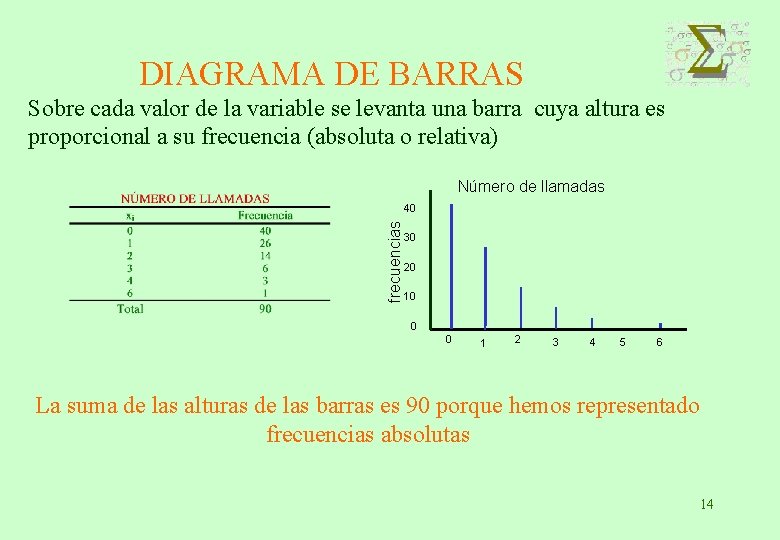
DIAGRAMA DE BARRAS Sobre cada valor de la variable se levanta una barra cuya altura es proporcional a su frecuencia (absoluta o relativa) Número de llamadas frecuencias 40 30 20 10 0 0 1 2 3 4 5 6 La suma de las alturas de las barras es 90 porque hemos representado frecuencias absolutas 14

HISTOGRAMA Cada clase se representa mediante un rectángulo cuyo área es proporcional a su frecuencia (absoluta o relativa) La altura de cada rectángulo es el cociente entre el área (frecuencia) y la base (amplitud del intervalo) o proporcional a dicho cociente 15

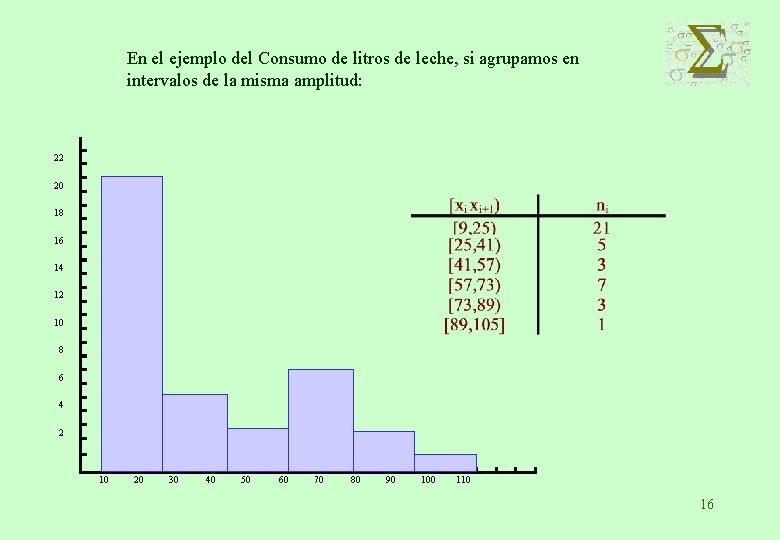
En el ejemplo del Consumo de litros de leche, si agrupamos en intervalos de la misma amplitud: 22 20 18 16 14 12 10 8 6 4 2 10 20 30 40 50 60 70 80 90 100 110 16

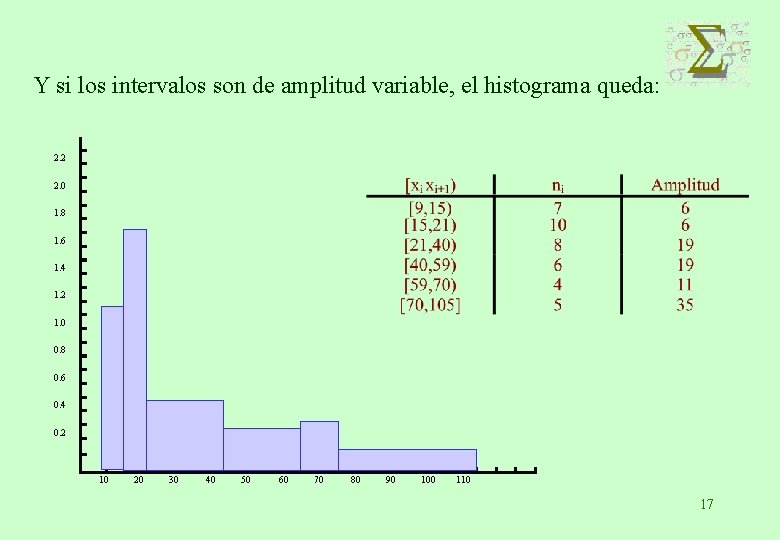
Y si los intervalos son de amplitud variable, el histograma queda: 2. 2 2. 0 1. 8 1. 6 1. 4 1. 2 1. 0 0. 8 0. 6 0. 4 0. 2 10 20 30 40 50 60 70 80 90 100 110 17

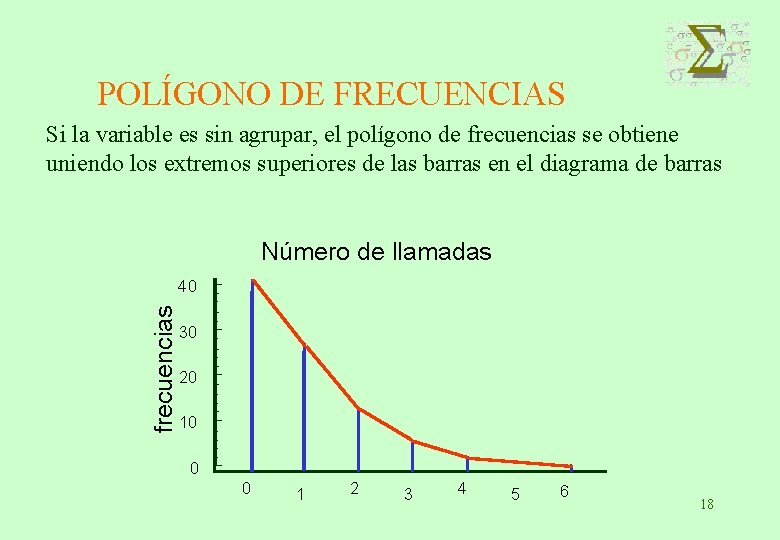
POLÍGONO DE FRECUENCIAS Si la variable es sin agrupar, el polígono de frecuencias se obtiene uniendo los extremos superiores de las barras en el diagrama de barras Número de llamadas frecuencias 40 30 20 10 0 0 1 2 3 4 5 6 18

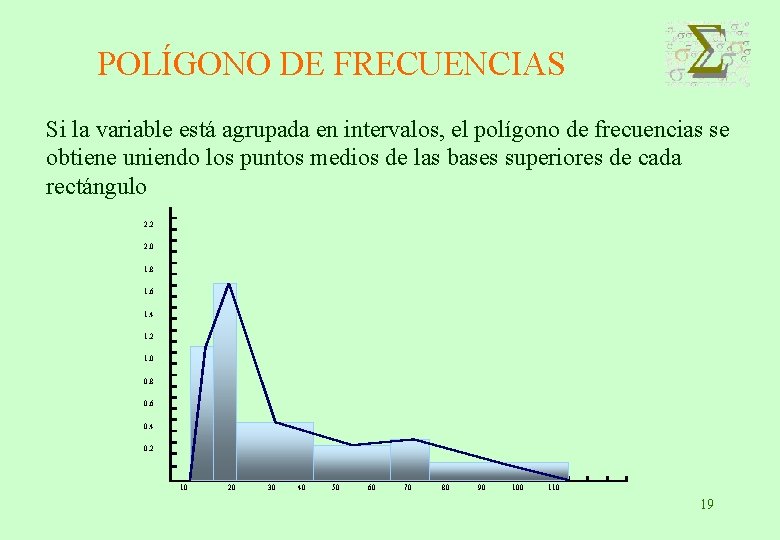
POLÍGONO DE FRECUENCIAS Si la variable está agrupada en intervalos, el polígono de frecuencias se obtiene uniendo los puntos medios de las bases superiores de cada rectángulo 2. 2 2. 0 1. 8 1. 6 1. 4 1. 2 1. 0 0. 8 0. 6 0. 4 0. 2 10 20 30 40 50 60 70 80 90 100 110 19

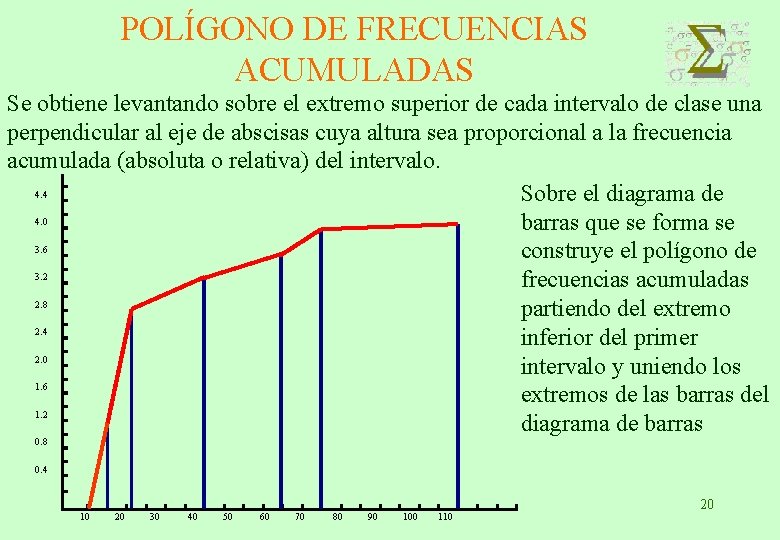
POLÍGONO DE FRECUENCIAS ACUMULADAS Se obtiene levantando sobre el extremo superior de cada intervalo de clase una perpendicular al eje de abscisas cuya altura sea proporcional a la frecuencia acumulada (absoluta o relativa) del intervalo. 4. 4 Sobre el diagrama de 4. 0 barras que se forma se 3. 6 construye el polígono de 3. 2 frecuencias acumuladas 2. 8 partiendo del extremo 2. 4 inferior del primer 2. 0 intervalo y uniendo los 1. 6 extremos de las barras del 1. 2 diagrama de barras 0. 8 0. 4 10 20 30 40 50 60 70 80 90 100 110 20

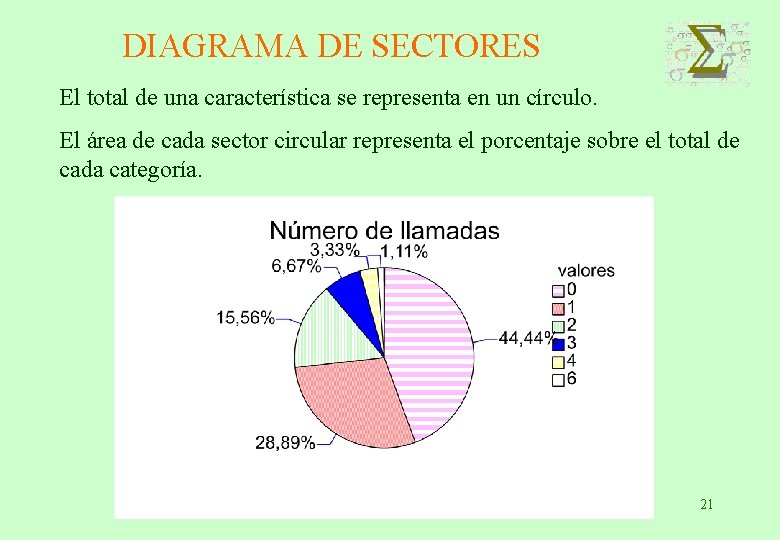
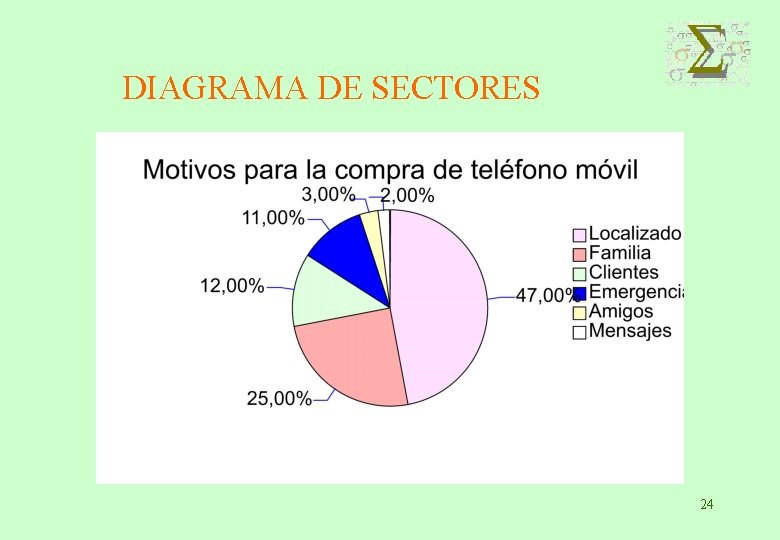
DIAGRAMA DE SECTORES El total de una característica se representa en un círculo. El área de cada sector circular representa el porcentaje sobre el total de cada categoría. 21

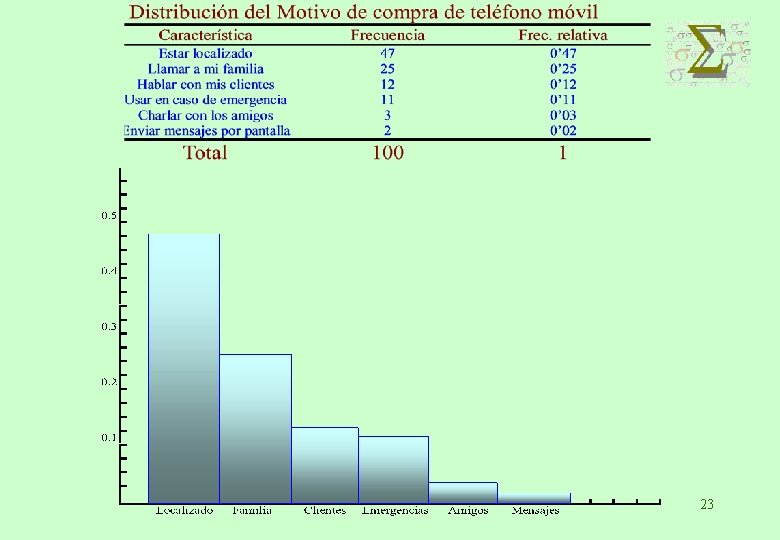
DIAGRAMA DE RECTÁNGULOS Cada categoría o modalidad se representa por un rectángulo cuya altura es proporcional a su frecuencia. Todos los rectángulos tienen la misma base. Si se ordenan las categorías o clases por sus frecuencias (de mayor a menor frecuencia) se suele llamar a este gráfico diagrama de Pareto 22

23

DIAGRAMA DE SECTORES 24

Otras representaciones gráficas 25

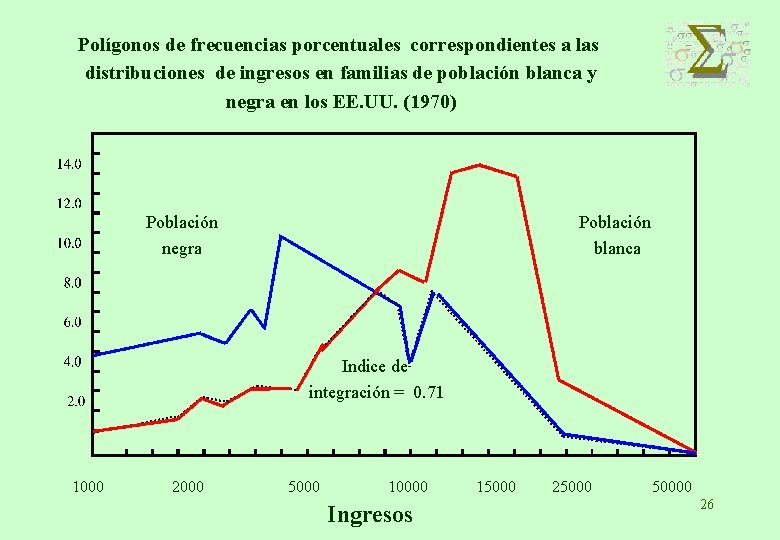
Polígonos de frecuencias porcentuales correspondientes a las distribuciones de ingresos en familias de población blanca y negra en los EE. UU. (1970) Población negra Población blanca Indice de integración = 0. 71 1000 2000 5000 10000 Ingresos 15000 250000 26

Diagrama de estrella llave o perfil radial 27

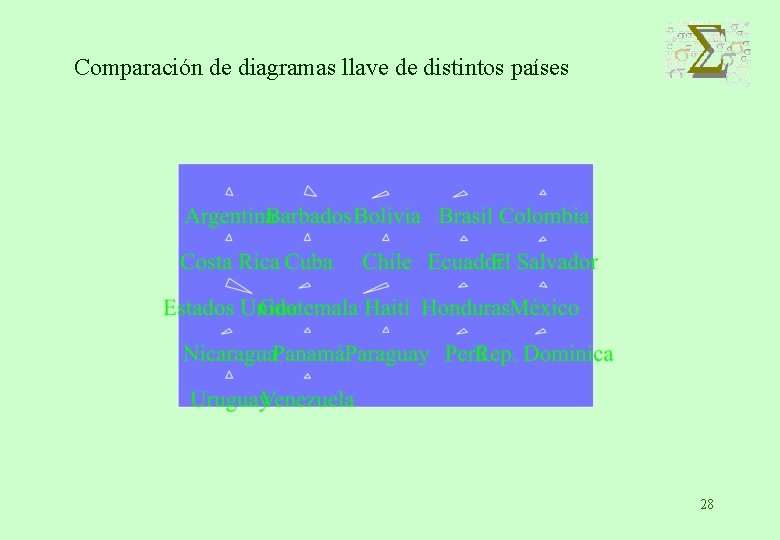
Comparación de diagramas llave de distintos países 28

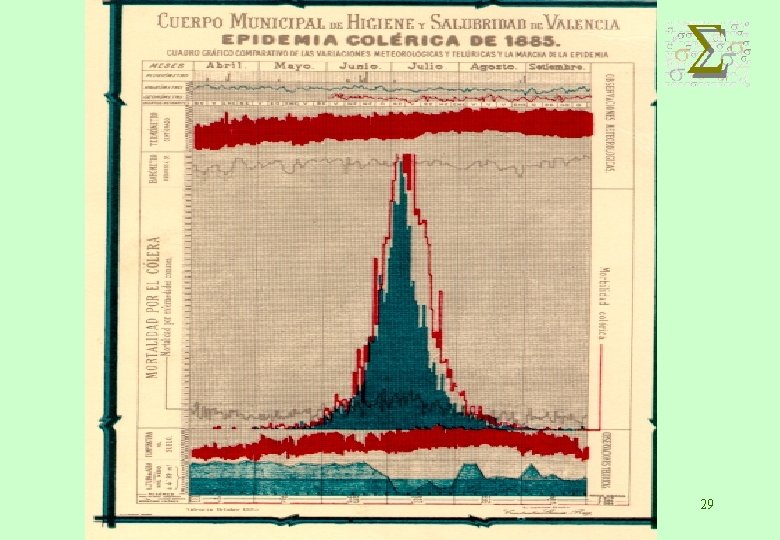
29

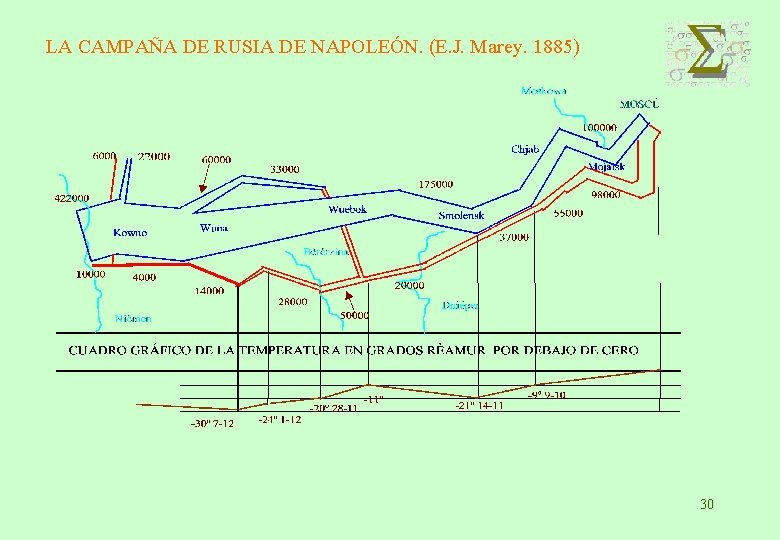
LA CAMPAÑA DE RUSIA DE NAPOLEÓN. (E. J. Marey. 1885) 30

MÉTODOS ANALÍTICOS MEDIDAS DE TENDENCIA CENTRAL • Moda • Mediana • Cuantiles: cuartiles, deciles y percentiles MEDIDAS DE DISPERSIÓN • Rango o recorrido • Recorrido intercuartílico • Varianza y desviación típica • Desviación media • Coeficientes de variación MEDIDAS DE FORMA • Coeficientes de asimetría 31

1. 4 MEDIDAS DE TENDENCIA CENTRAL MODA, Mo: Es el dato que más se repite. Puede haber más de una moda. Por ejemplo, con los datos muestrales: 2, 2, 3, 3, 4, 4, 4, 5, 6, 6, 6, 7, 7, 8, 8 se tienen dos modas: 4 y 6. MEDIA ARITMÉTICA: Con los datos anteriores, se tiene: 32

MEDIANA Me: Es un valor tal que, ordenados en magnitud los datos, el 50% es menor que él y el 50% mayor. 2233444 5 6667788 CUANTIL DE ORDEN , C : Es un valor tal que, ordenados en magnitud los datos, el 100 % es menor que él y el resto mayor. Utilizaremos los cuartiles Q 1, Q 2, Q 3 , los deciles D 1, . . . , D 9 y los percentiles P 1, . . . , P 99 que corresponden a cuantiles con = 0. 25, 0. 75, = 0. 1, . . . , 0. 9 y = 0. 01, . . . , 0. 99 respectivamente. 33

Cálculo de cuantiles: (mediana, cuartiles y percentiles) • Se ordenan los datos de menor a mayor. • Se determina el valor n. Donde n es el numero de datos el orden del cuantil queremos calcular • Si n no es entero, entero se redondea al siguientero y el dato que ocupe ese lugar es el cuantil buscado. • Si n = k es entero el cuantil buscado es la media entre xk y xk+1. 2, 2, 3, 3, 4, 4, 4, 5, 6, 6, 6, 7, 7, 8, 8 en este ejemplo n=15 La mediana será: Me = C 0. 5, es decir n =15*0. 5 = 7. 5, luego la mediana ocupa el lugar 8, x 8 =Me=5 El segundo decil D 2 = C 0. 2, es decir n =15*0. 2=3, luego D 2 es la media 34 entre x 3 y x 4, D 2=3

ROBUSTEZ DE LA MEDIANA Consideremos los datos del ejemplo anterior: 223344456667788 Si añadimos un nuevo dato x 16 = 34 y calculamos de nuevo la media y la mediana, obtenemos: • Nueva media: = 6. 8 • Nueva mediana: Me = 5. 5 35

COMPARACIÓN MEDIA-MEDIANA • La media contiene más información porque usa los valores de todos los datos. • La mediana es más robusta frente a los cambios en los datos. • La media es más sencilla de calcular y se presta mejor a los cálculos algebraicos. • Deben calcularse ambas pues proporcionan información complementaria. 36

1. 5 MEDIDAS DE DISPERSIÓN Las medidas de centralización proporcionan una información incompleta del conjunto de datos. Ejemplo: sean X e Y las notas de dos grupos de cuarenta alumnos, con distribuciones de frecuencias: Para ambas variables la media es 5, pero en el segundo caso 5 es un valor más representativo de los datos que en el primero. Las medidas de dispersión nos permiten valorar si el valor de la medida de tendencia central es , o no es , representativo. 37

MEDIDAS DE DISPERSIÓN Partimos de una muestra de tamaño n=15, 2 2 3 3 4 4 4 5 6 6 6 7 7 8 8 8 -2=6 • RANGO O RECORRIDO: R = Max-Min = • RECORRIDO INTERCUARTÍLICO: RQ = Q 3 - Q 1 = • VARIANZA: 7 -3 = 4 3. 87 4. 14 • CUASIVARIANZA: • DESVIACIÓN TÍPICA: • CUASIDESVIACIÓN TÍPICA: = 1. 97 = 2. 04 38

• DESVIACIÓN MEDIA: = 1. 73 • COEFICIENTE DE VARIACIÓN DE PEARSON: = 0. 394 • COEFICIENTE DE VARIACIÓN MEDIA: = 0. 347 39

Ejemplo de cómo la varianza no sirve para comparar la dispersión de dos variables distintas: Sea X el peso en Kg de una población de lagartos Sea Y el peso en Kg de una población de tiburones x = 0. 473, CV = 0. 34 V = 0. 026 y = 404, V = 9. 846 CV = 0. 0076 40

DESIGUALDAD DE CHEBYCHEV Entre la media y k veces la desviación típica se encuentran, como mínimo el de los datos. Por ejemplo, si la media es 500 y la desviación típica es 20, en el intervalo: estarán, como mínimo, el de las observaciones. 41

1. 6 MEDIDAS DE ASIMETRÍA • COEFICIENTE DE ASIMETRÍA DE FISHER: • COEFICIENTE DE ASIMETRÍA DE PEARSON: 42

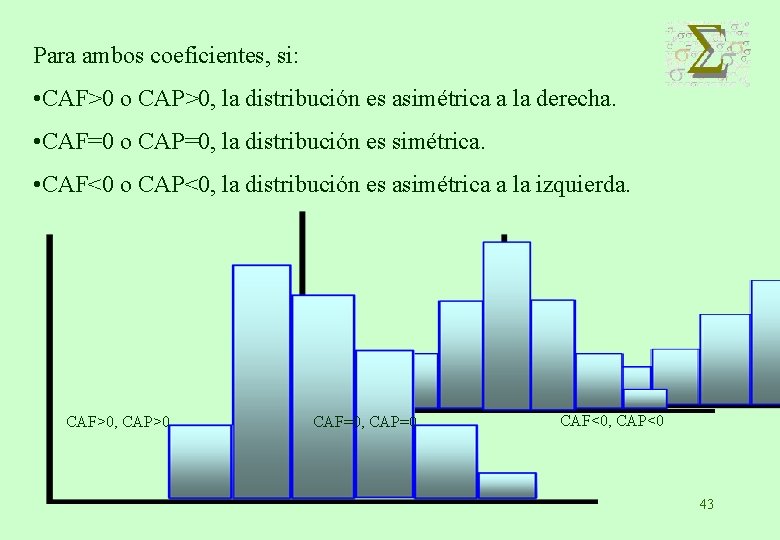
Para ambos coeficientes, si: • CAF>0 o CAP>0, la distribución es asimétrica a la derecha. • CAF=0 o CAP=0, la distribución es simétrica. • CAF<0 o CAP<0, la distribución es asimétrica a la izquierda. CAF>0, CAP>0 CAF=0, CAP=0 CAF<0, CAP<0 43

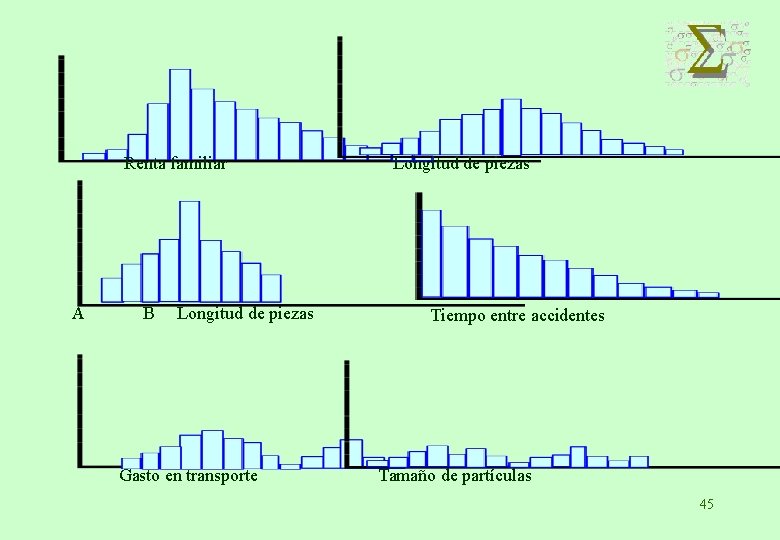
Información que se puede extraer de un histograma: 44

Renta familiar A B Longitud de piezas Gasto en transporte Longitud de piezas Tiempo entre accidentes Tamaño de partículas 45

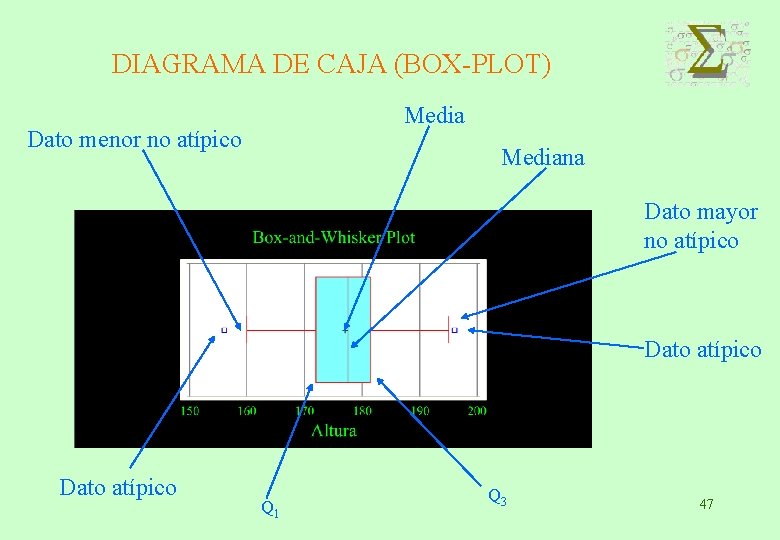
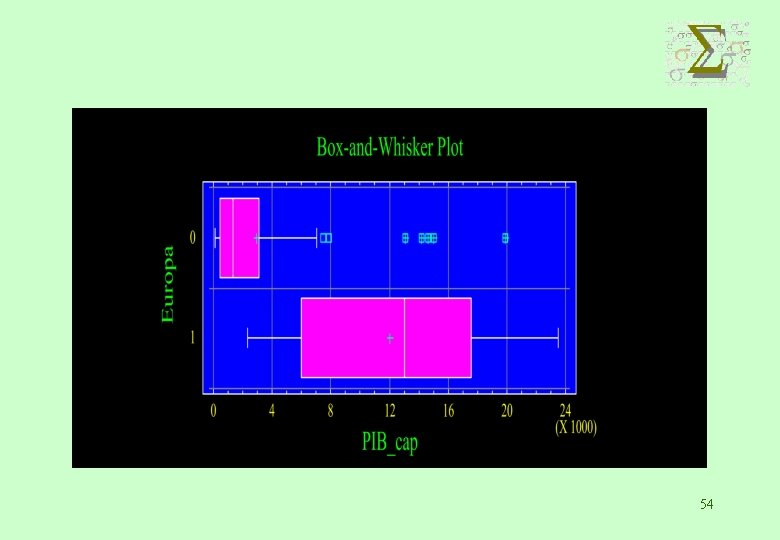
DIAGRAMA DE CAJA (BOX-PLOT) Se construye del siguiente modo: • Con los datos ordenados se obtienen los tres cuartiles • Se dibuja un rectángulo cuyos extremos son Q 1 y Q 3 y se indica la posición de la mediante una línea. • Se calculan los límites de admisión ( los valores queden fuera se consideran atípicos) • Se dibuja una línea desde cada extremo del rectángulo hasta el valor más alejado no atípico. • Se marcan todos los datos considerados como atípicos. 46

DIAGRAMA DE CAJA (BOX-PLOT) Media Dato menor no atípico Mediana Dato mayor no atípico Dato atípico Q 1 Q 3 47

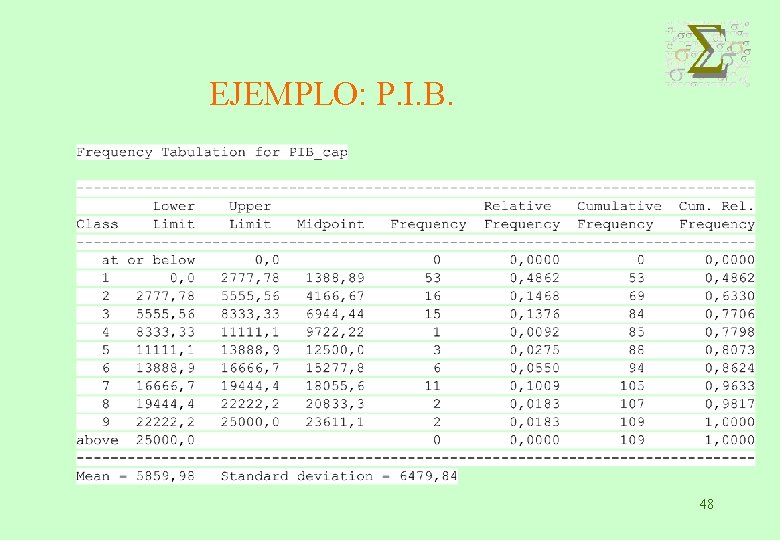
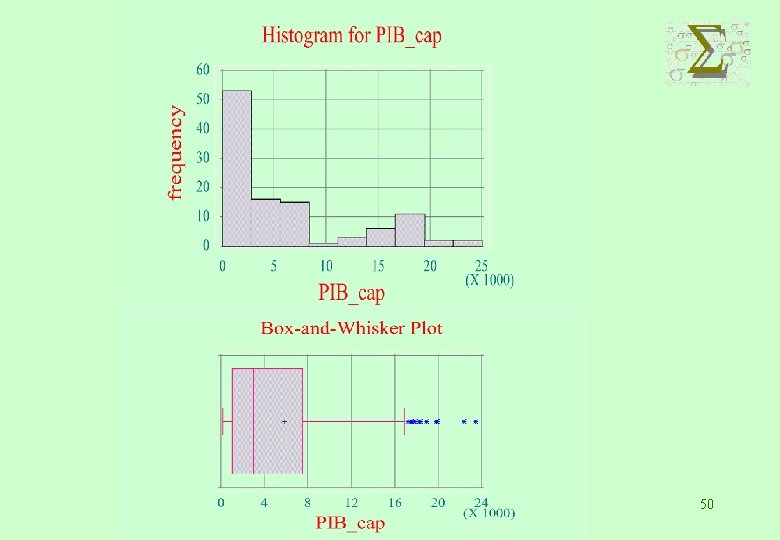
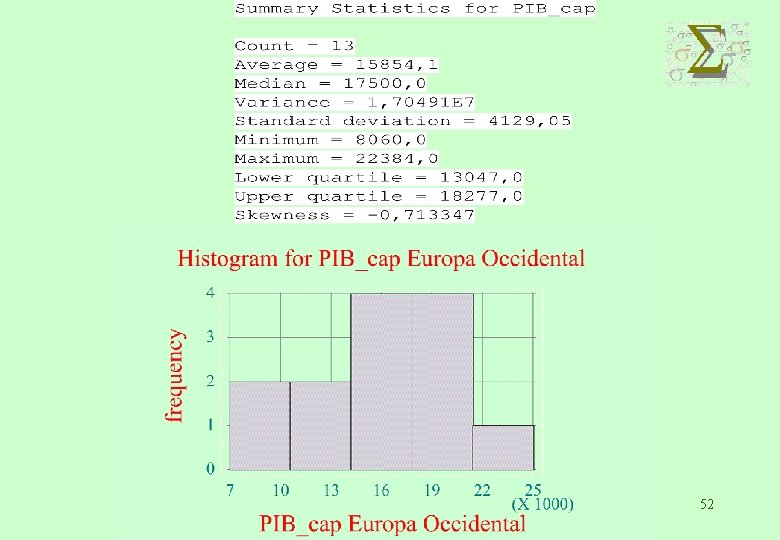
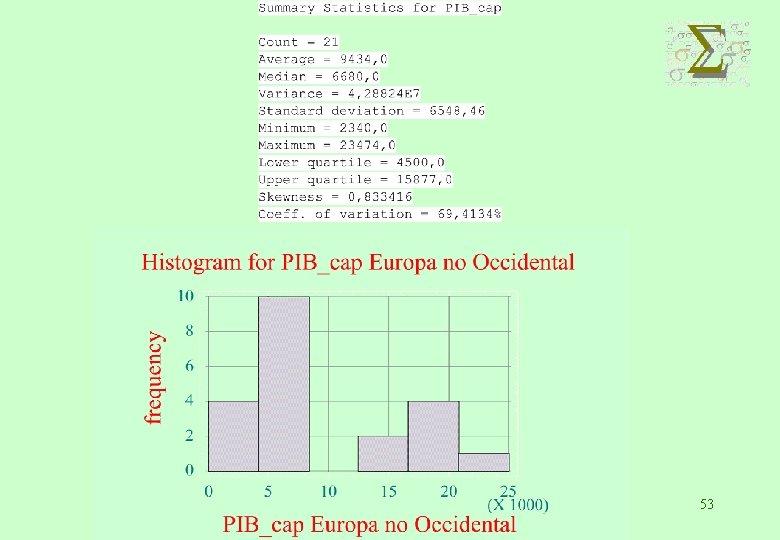
EJEMPLO: P. I. B. 48

49

50

51

52

53

54

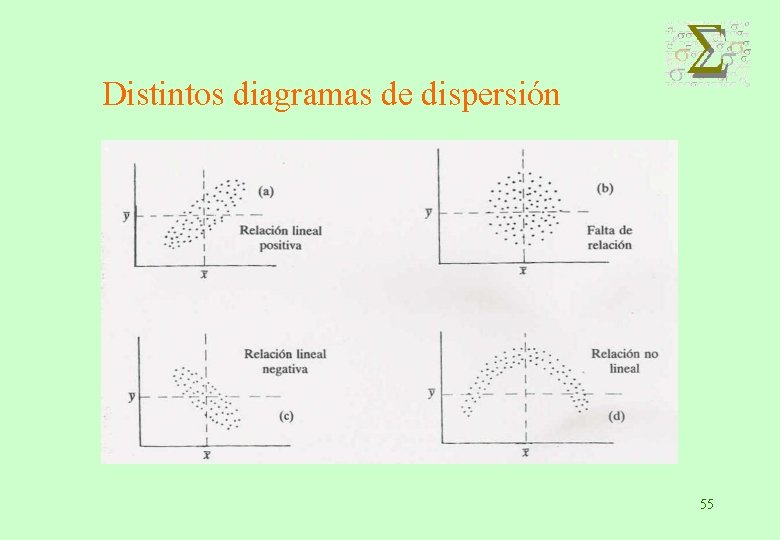
Distintos diagramas de dispersión 55

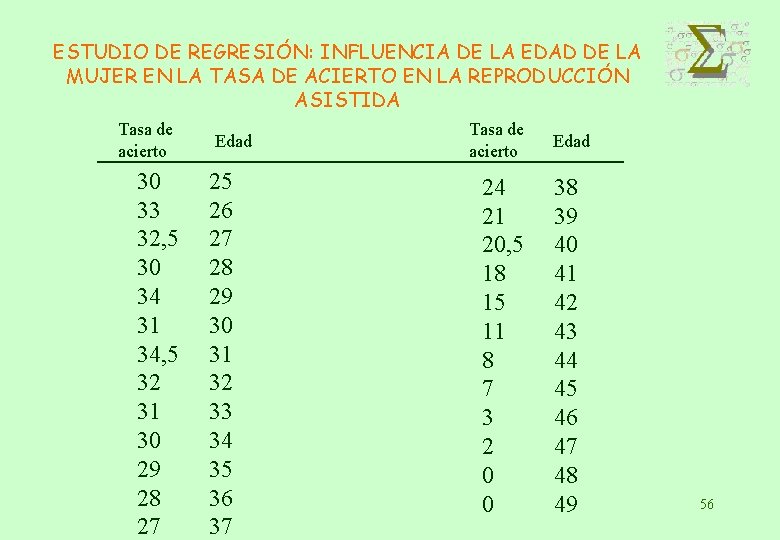
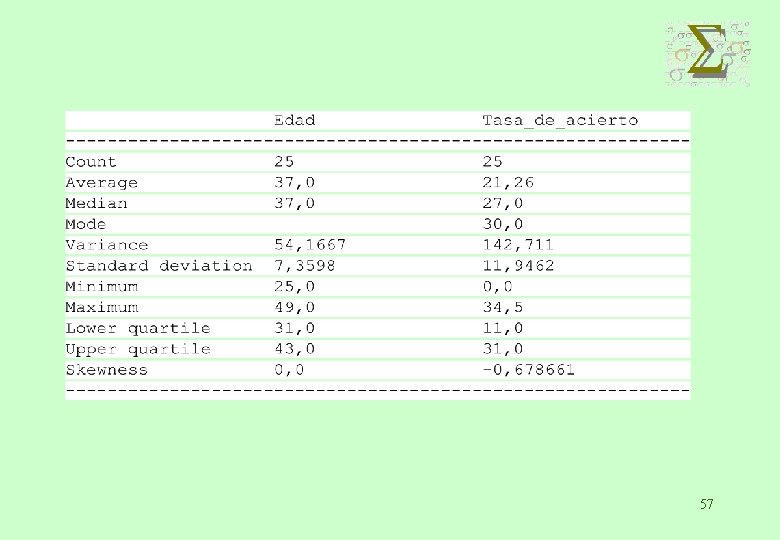
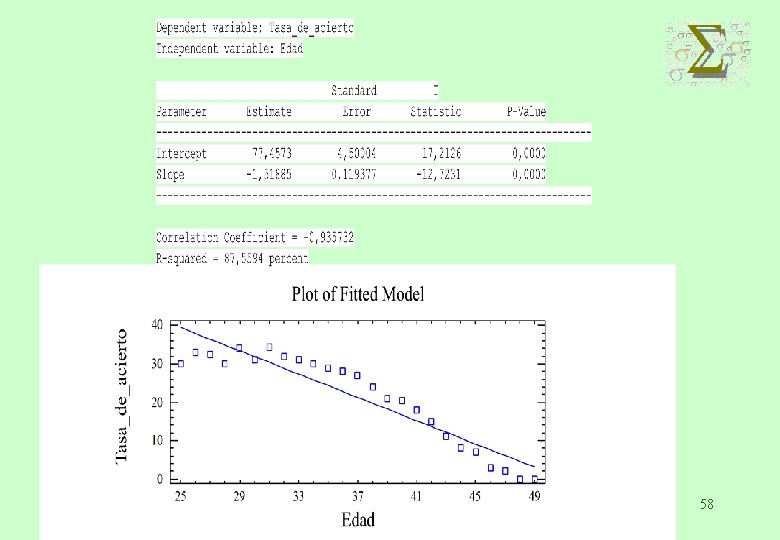
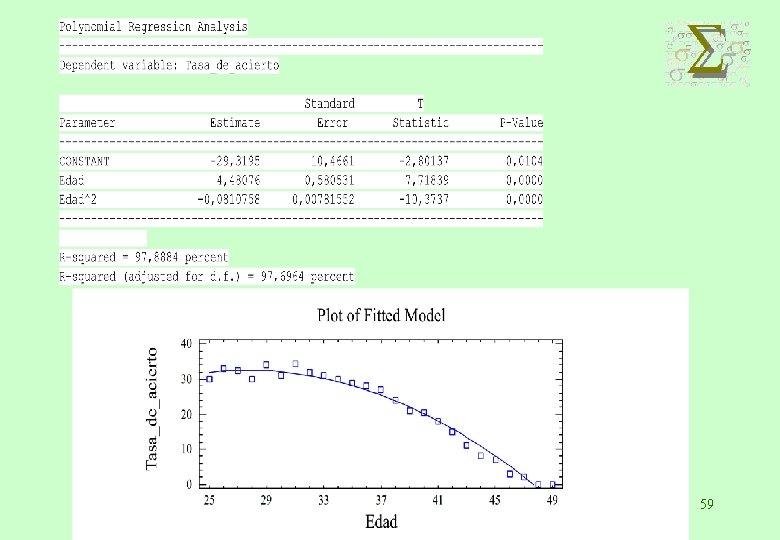
ESTUDIO DE REGRESIÓN: INFLUENCIA DE LA EDAD DE LA MUJER EN LA TASA DE ACIERTO EN LA REPRODUCCIÓN ASISTIDA Tasa de acierto 30 33 32, 5 30 34 31 34, 5 32 31 30 29 28 27 Edad 25 26 27 28 29 30 31 32 33 34 35 36 37 Tasa de acierto 24 21 20, 5 18 15 11 8 7 3 2 0 0 Edad 38 39 40 41 42 43 44 45 46 47 48 49 56

57

58

59