CSE 3813 Introduction to Formal Languages and Automata






















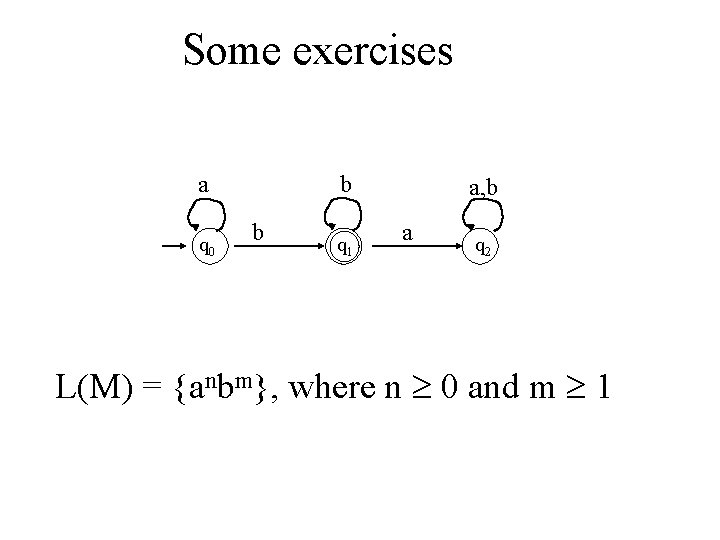




























- Slides: 94

CSE 3813 Introduction to Formal Languages and Automata Chapter 2 Deterministic finite automata These class notes are based on material from our textbook, An Introduction to Formal Languages and Automata, 4 th ed. , by Peter Linz, published by Jones and Bartlett Publishers, Inc. , Sudbury, MA, 2006. They are intended for classroom use only and are not a substitute for reading the textbook.

Review of set notation formal languages wn denotes a string obtained by concatenating w n times w 0 = λ {a, b}* denotes all strings over the alphabet {a, b}

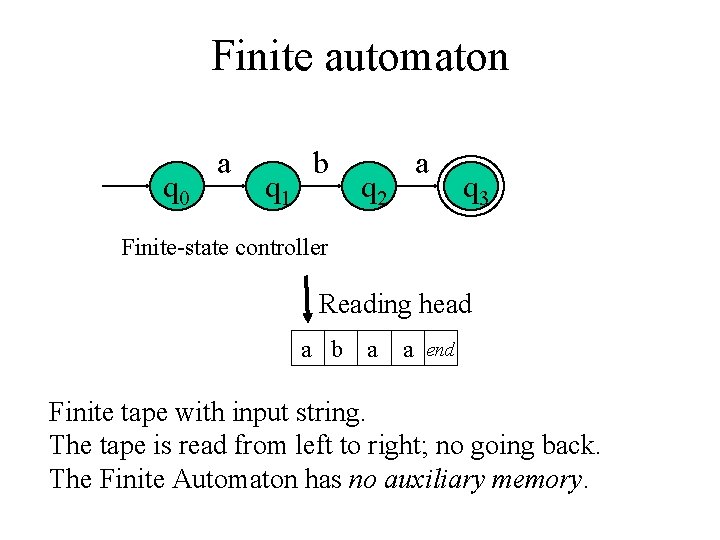
Finite automaton q 0 a q 1 b q 2 a q 3 Finite-state controller Reading head a b a a end Finite tape with input string. The tape is read from left to right; no going back. The Finite Automaton has no auxiliary memory.

Deterministic Finite Accepter Defined by a quintuple: M = (Q, , , q 0, F) Q is a finite, nonempty set of states is finite set of input symbols called alphabet : Q Q is the transition function q 0 Q is the initial state F Q is a set of final or “accepting” states In a deterministic finite accepter (DFA), each transition is completely determined by the current state and current input symbol.

Deterministic Finite Accepter Example: M = ({q 0, q 1, q 2}, {a, b}, , q 0, {q 1}) Q = {q 0, q 1, q 2} = {a, b} is the transition function (see next slide) q 0 is the initial state {q 1} is the set of final states In a deterministic finite automaton (DFA), each transition is completely determined by the current state and current input symbol

Transition table The transition function of a finite automaton can be represented by a table: state q 0 q 1 q 2 input a b a b next state q 0 q 1 q 2 q 2 For a DFA, δ is a total function; that is, there is one and only one entry for each combination of state and input symbol. The transition function can be regarded as a “program. ”

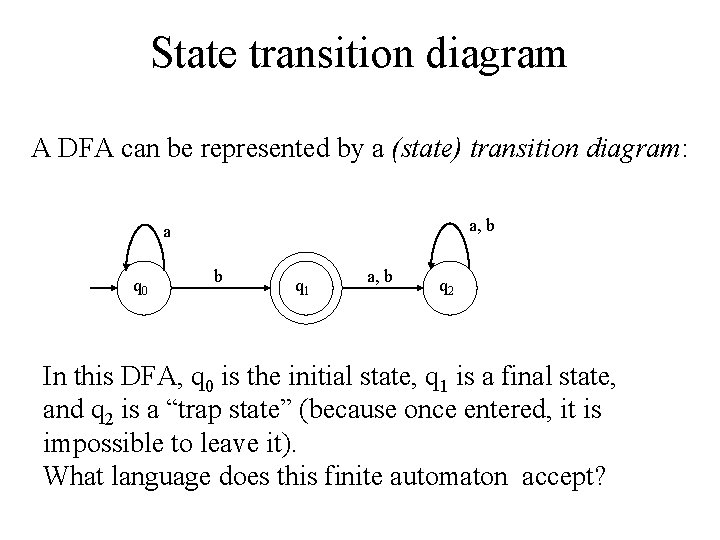
State transition diagram A DFA can be represented by a (state) transition diagram: a, b a q 0 b q 1 a, b q 2 In this DFA, q 0 is the initial state, q 1 is a final state, and q 2 is a “trap state” (because once entered, it is impossible to leave it). What language does this finite automaton accept?

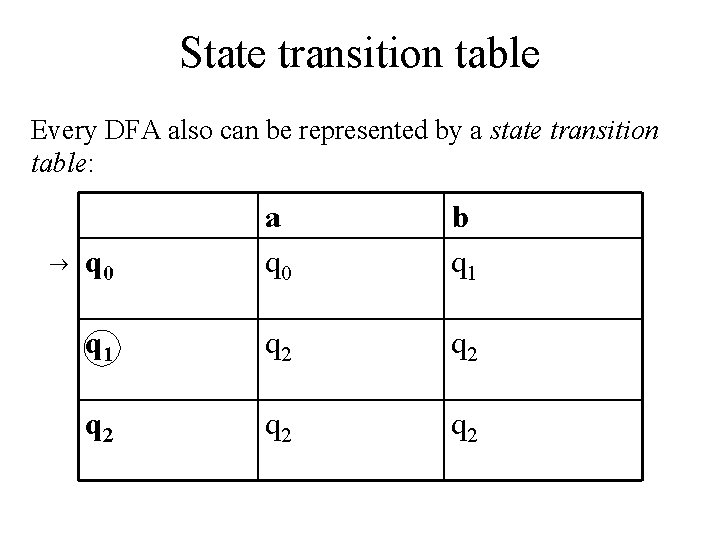
State transition table Every DFA also can be represented by a state transition table: q 0 a q 0 b q 1 q 2 q 2 q 2

Configuration of a DFA A configuration summarizes the information about past inputs that is needed to determine the behavior of the automaton on subsequent inputs: • the current state • the contents of the tape that have not been read, that is, that are to the right of the read/write head • notation: (q 3, aba) Current state Contents of tape that have not been read yet

“Yields” relation • Indicates a transition from one configuration of a DFA to the next configuration, which is equivalent to one step in a computation • notation: (q 0, abba) |= (q 1, bba) • |=n denotes a transition from one configuration of a DFA to another after n steps • |=* denotes the reflexive, transitive closure of the relation |=, i. e. , it denotes a transition from one configuration of a DFA to another after zero or more steps

Extended transition function • The extended transition function is represented by: δ* : Q * Q • The * denotes a string instead of a single character. • Q will represent the state the automaton will be in after reading the entire string instead of a single character.

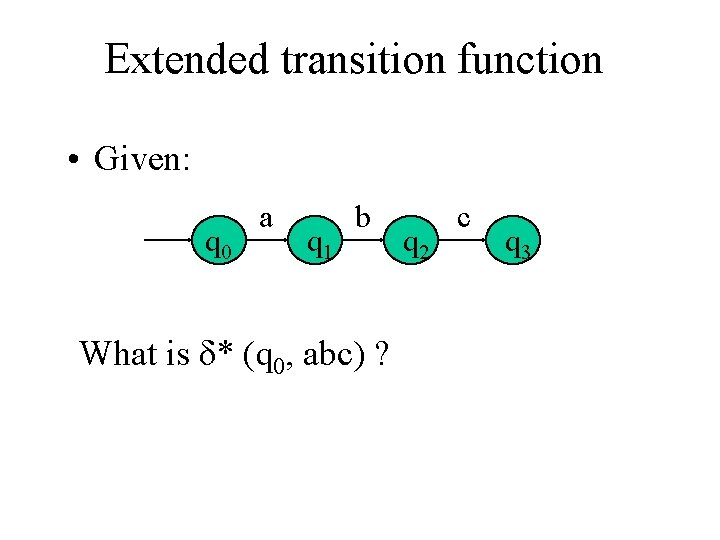
Extended transition function • Given: q 0 a q 1 b What is δ* (q 0, abc) ? q 2 c q 3

Extended transition function Let M = (Q, , q 0, , A) be an FA. We can define the function * : Q * Q as follows: • For any q Q, * (q, ) = q • For any y * , and q Q, * (q, ya) = ( * (q, y) , a)

Computation • Since a DFA is an abstract model of computation, we can now define mathematically what we mean by “computation” • A computation is a sequence of transitions from one configuration to another • A computation proceeds according to a finite set of rules or instructions -- the transition function (or program) of the DFA

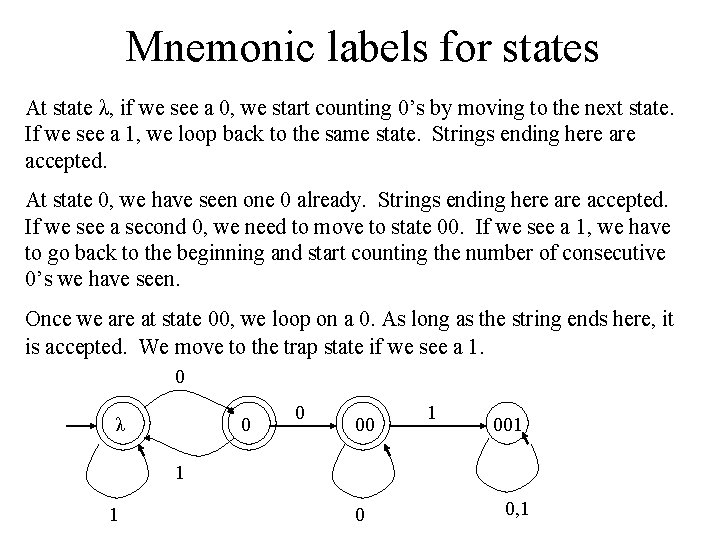
Mnemonic labels for states We don’t have to label our states with qsubscript. We can give them mnenonic labels that remind us of how we got to that particular state. This can help us decide how to build an automaton. For example, let’s find a DFA that accepts all strings on {0, 1} except those containing the string 001.

Mnemonic labels for states The string λ is accepted by this DFA, so the start state must be an accepting state. Let’s label it λ. If our string starts off 001, it must be rejected. So we know that there must be a consecutive path from the start state to a trap state via three arcs labeled 0, 0, and 1. Let’s label that state 001. We can see that along this path there must be two other states labeled 0 and 00. Strings ending in 0 are accepted, so these are accepting states. So far we have: λ 0 00 1 001

Mnemonic labels for states At state λ, if we see a 0, we start counting 0’s by moving to the next state. If we see a 1, we loop back to the same state. Strings ending here accepted. At state 0, we have seen one 0 already. Strings ending here accepted. If we see a second 0, we need to move to state 00. If we see a 1, we have to go back to the beginning and start counting the number of consecutive 0’s we have seen. Once we are at state 00, we loop on a 0. As long as the string ends here, it is accepted. We move to the trap state if we see a 1. 0 λ 0 0 00 1 001 1 1 0 0, 1

The language accepted by a DFA • The language accepted by a DFA M is denoted L(M) • It is the set of all strings such that, when M starts in its initial configuration, it ends up in an accepting configuration.

Accepting Let M = (Q, , q 0, , F) be an FA. • A string w * is accepted by M if *(q 0, w) F • The language accepted (or recognized) by M is the set of all strings on that are accepted by M • Formally: L(M) = {w * : δ* (q 0, w) F}

Rejecting Here is a DFA that accepts any string: q 0 (anything) The power of a machine lies in its ability to discriminate - to accept only some strings as belonging to a language, and to reject all others.

Regular languages • A language L over the alphabet is regular iff (if and only if) there is a Deterministic Finite Automaton that accepts L.

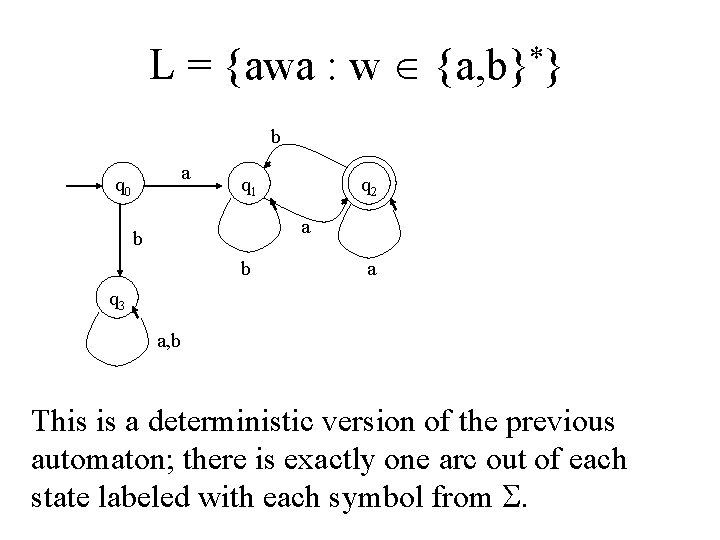
Regular languages Show that the language L = {awa : w {a, b}*} is regular. To do this, all we have to do is construct a DFA that accepts this language

L = {awa : w {a, b}*} a q 0 q 1 a q 2 b a, b q 3 This finite accepter accepts all and only the strings of the language given above. But note that there are two arcs out of q 1 labeled a. How does the FA know which path to take on an a? It doesn’t; it has to magically guess right. Also, there are no arcs out of q 2. So this FA is nondeterministic.

Nondeterminism A finite automaton is deterministic if: from every node there is exactly one arc labeled for each character in the alphabet of the language

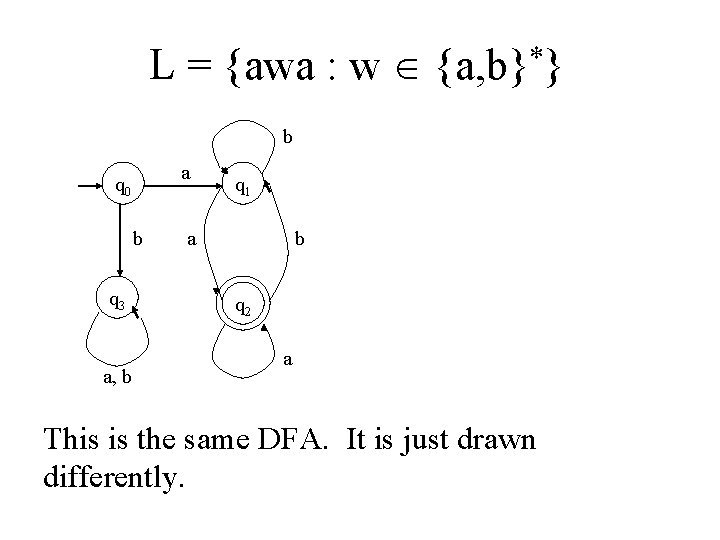
L = {awa : w {a, b}*} b a q 0 q 1 q 2 a b b a q 3 a, b This is a deterministic version of the previous automaton; there is exactly one arc out of each state labeled with each symbol from .

L = {awa : w {a, b}*} b a q 0 b q 3 a, b q 1 a b q 2 a This is the same DFA. It is just drawn differently.

Nondeterministic finite accepters Actually, any nondeterministic FA can be turned into a deterministic FA. That is why this class of automata is called Deterministic Finite Accepters.

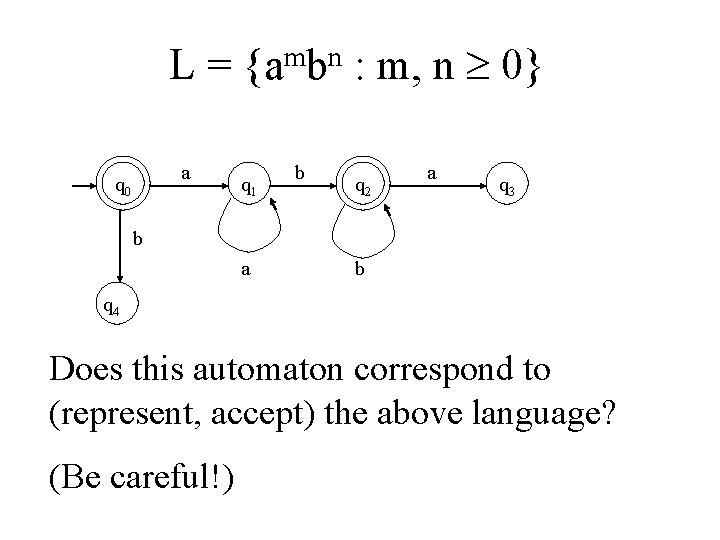
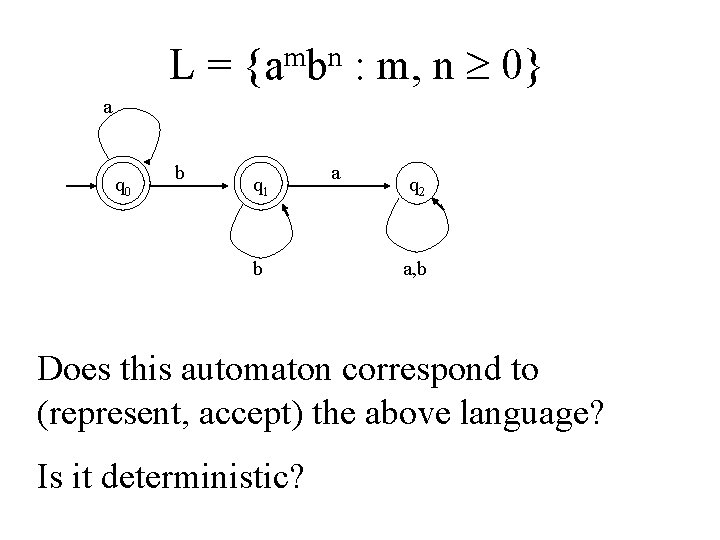
Deterministic finite accepters L = {ambn : m, n 0} Give a DFA that accepts this language

L = {ambn : m, n 0} What do we know about this language’s automaton? • Will it accept the empty string? If so, how do we represent that? • Will it accept strings that begin with an a? • Having begun with an a, seeing indefinitely many more a’s are OK ; the automaton can loop here. • Will it accept strings that begin with a b? • Once it sees a b, the automaton now has to be on guard. • As long as it continues to see b’s , it’s OK; loop. • If the string ends here, accept. • If it sees an a after seeing a b, reject.

L = {ambn : m, n 0} a q 0 q 1 b q 2 a q 3 b a b q 4 Does this automaton correspond to (represent, accept) the above language? (Be careful!)

L = {ambn : m, n 0} a q 0 b q 1 b a q 2 a, b Does this automaton correspond to (represent, accept) the above language? Is it deterministic?

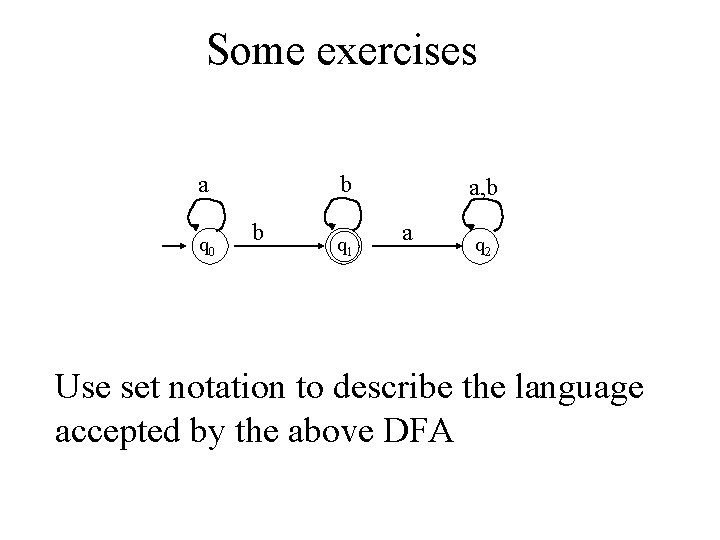
Some exercises a q 0 b b q 1 a, b a q 2 Use set notation to describe the language accepted by the above DFA
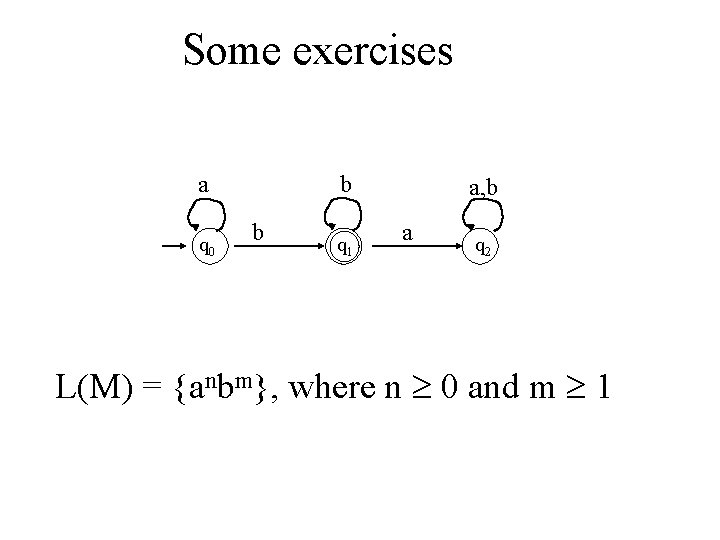
Some exercises a q 0 b b q 1 a, b a q 2 L(M) = {anbm}, where n 0 and m 1

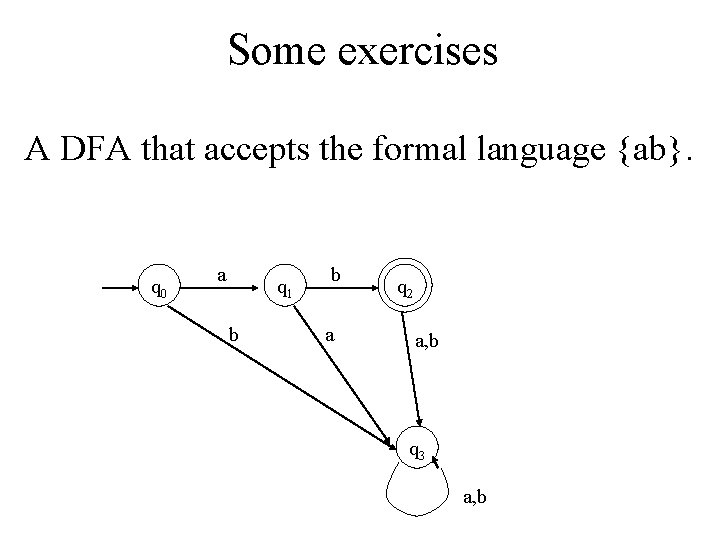
Some exercises Give a DFA that accepts the formal language {ab}.

Some exercises A DFA that accepts the formal language {ab}. q 0 a q 1 b b a q 2 a, b q 3 a, b

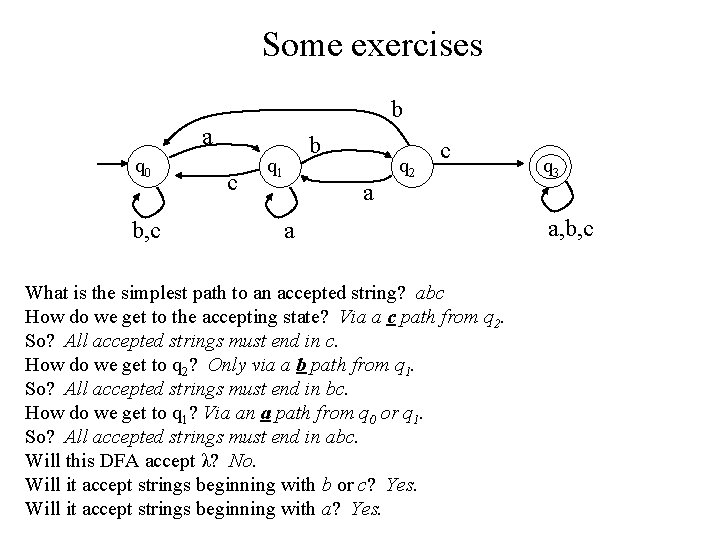
Some exercises Use set notation to describe the language accepted by the following DFA. b a q 0 b, c c q 1 a b a q 2 c q 3 a, b, c Homework: Can you give a DFA that accepts the complement of this language?

Some exercises b a q 0 b, c c q 1 b a q 2 c a What is the simplest path to an accepted string? abc How do we get to the accepting state? Via a c path from q 2. So? All accepted strings must end in c. How do we get to q 2? Only via a b path from q 1. So? All accepted strings must end in bc. How do we get to q 1? Via an a path from q 0 or q 1. So? All accepted strings must end in abc. Will this DFA accept λ? No. Will it accept strings beginning with b or c? Yes. Will it accept strings beginning with a? Yes. q 3 a, b, c

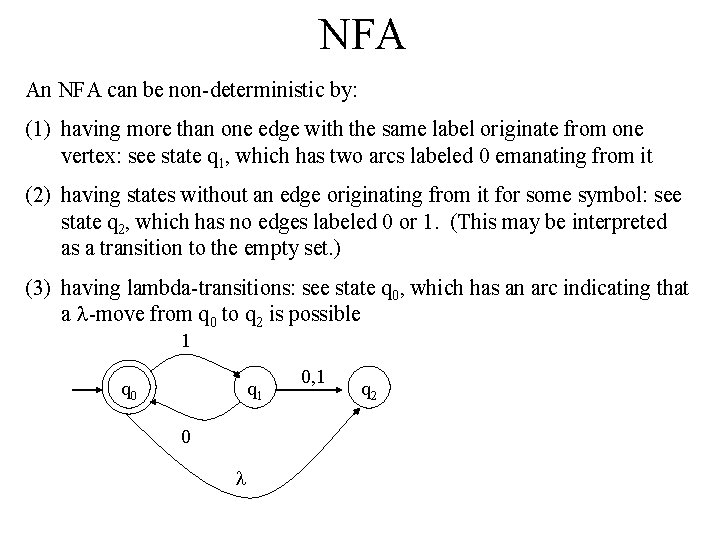
NFA A non-deterministic finite accepter (abbreviated NFA or NDFA) is defined by the quintuple: M = (Q, , , q 0, F) Q is a finite, nonempty set of states is finite set of input symbols called alphabet : Q ( { }) 2 Q is the transition function q 0 Q is the initial state F Q is a set of final or “accepting” states

NFA An NFA can be non-deterministic by: (1) having more than one edge with the same label originate from one vertex: see state q 1, which has two arcs labeled 0 emanating from it (2) having states without an edge originating from it for some symbol: see state q 2, which has no edges labeled 0 or 1. (This may be interpreted as a transition to the empty set. ) (3) having lambda-transitions: see state q 0, which has an arc indicating that a -move from q 0 to q 2 is possible 1 q 0 q 1 0 0, 1 q 2

NFA Differences between a DFA and an NFA: (1) in an NFA, the range of is in the powerset of Q (instead of just Q), so that from the current state, upon reading a symbol: (a) more than one state might be the next state of the NFA, or (b) no state may be defined as the next state of the NFA, and (2) -moves are possible; that is, a transition from one state to another may occur without reading a symbol from the input string.

DFA vs. NFA DFA: transition function δ: Q×Σ→Q NFA: transition function δ : Q × (Σ {λ}) → 2 Q examples δ(q 0, a) = q 1 examples δ(q 1, a) = {q 1, q 2} δ(q 1, b) = {} δ(q 1, λ) = {q 2}

NFA The extended transition function for an NFA is defined so that * (qi, w) contains qj iff there is a walk in the transition graph from qi to qj labeled w. The language L accepted by an NFA M = (Q, , , q 0, F) is defined as L(M) = {w * : δ* (q 0, w) F } That is, the language consists of all strings w for which there is a walk labeled w from the start state to a final state in the transition graph.

Ways to think about nondeterminism • An NFA always make the correct “guess” as to which path to follow • An NFA uses “backtracking” (systematically tries all possibilities) a a q 1 q 4 a q 0 a q 2 a b q 3 For a particular string, imagine a tree of possible state transitions, as illustrated above:

Advantages of nondeterminism • an NFA can be smaller, easier to construct and easier to understand than a DFA that accepts the same language • useful for proving some theorems • good introduction to nondeterminism in more powerful computational models, where nondeterminism plays an important role

NFA = DFA One kind of automaton is more powerful than another if it can accept and reject some kinds of languages that the other cannot. Two finite accepters are equivalent if both accept the same language, that is, L(M 1) = L(M 2) As mentioned previously, we can always find an equivalent DFA for any given NFA. Therefore, NFA’s are no more powerful than DFA’s.

Equivalence of NFA and DFA • We now show that DFAs and NFAs accept exactly the same set of languages. That is, nondeterminism does not make a finite automaton any more powerful. • To show that NFAs and DFAs accept the same class of languages, we show two things: – any language accepted by a DFA can also be accepted by some NFA (this is easy to show -how? ) – any language accepted by a NFA can also be accepted by some DFA (this is more difficult to show)

Proof strategy • To show that any language accepted by a NFA is also accepted by some DFA, we describe an algorithm that takes any NFA and converts it into a DFA that accepts the same language • The algorithm is called the “subset construction algorithm” • We can use mathematical induction (on the length of a string accepted by the automaton) to prove that the DFA that is constructed accepts the same language as the NFA. (See Theorem 2. 2 in Linz) • You don’t need to remember the proof -- but you do need to remember the algorithm!

Subset construction algorithm • What does it do? Given a NFA, it constructs a DFA that accepts the same language. • What is the key idea? The equivalent DFA simulates the NFA by keeping track of the possible states it could be in. Each state of the DFA corresponds to a subset of the set of states of the NFA -- hence, the name of the algorithm. • If the NFA has n states, the DFA can have as many as 2 n states (why? ), although it usually has many less.

The subset construction algorithm: • The initial state of the DFA is the set of all states the NFA can be in without reading any input. • For any state {qi, qj, …, qk} of the DFA and any input a, the next state of the DFA is the set of all states of the NFA that can result as next states if the NFA is in any of the states qi, qj, …, qk when it reads a. This includes states that can be reached by reading a followed by any number of λ-transitions. Use this rule to keep adding new states and transitions until it is no longer possible to do so. • The accepting states of the DFA are those states that contain an accepting state of the NFA.

NFA DFA Theorem 2. 2 in Linz: Let L be the language accepted by a nondeterministic finite accepter MN = (QN, , N, q 0, FN). Then there exists a deterministic finite accepter MD = (QD, , D, {q 0}, FD) such that L = L(MD). Proof by construction.

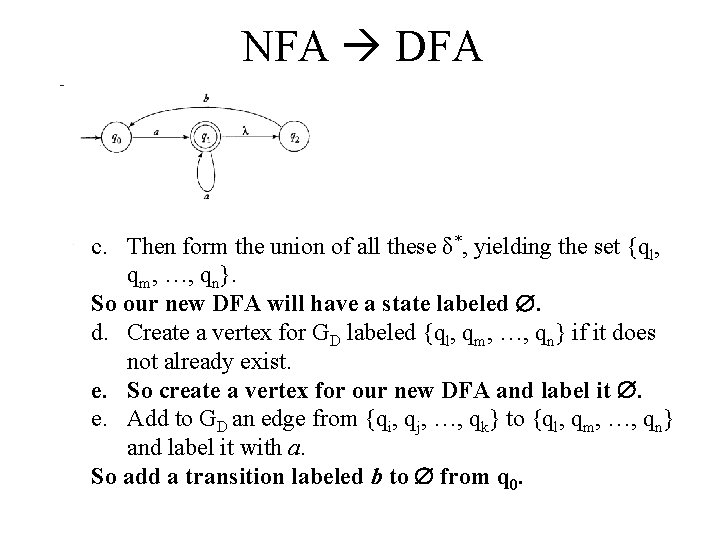
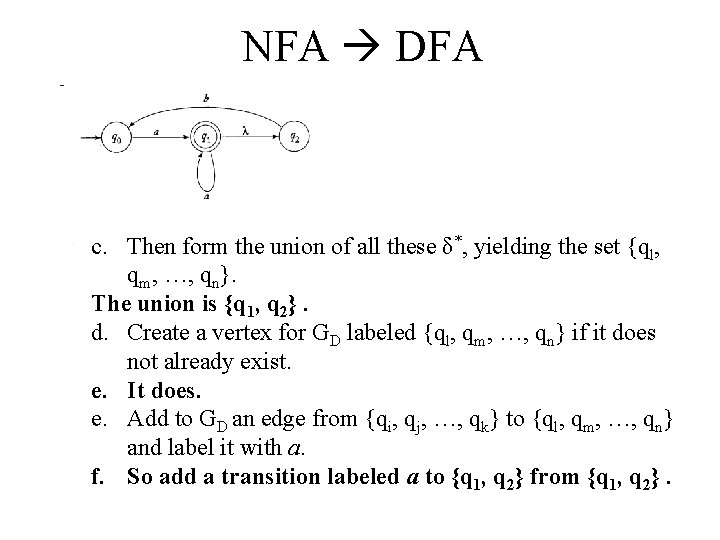
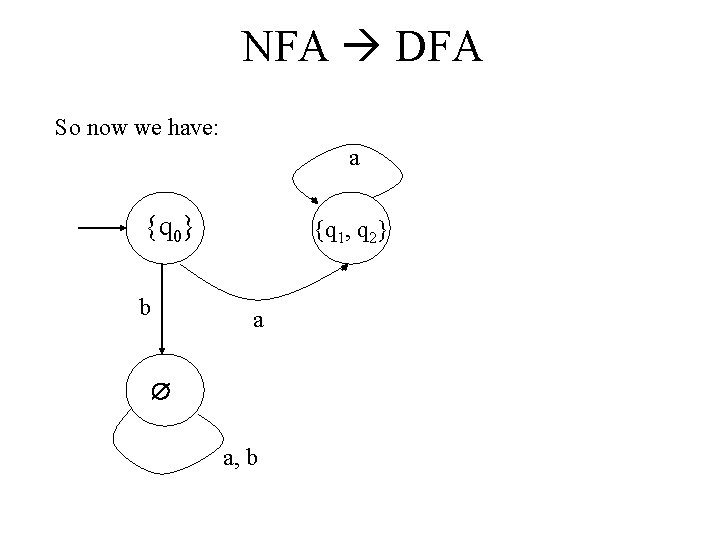
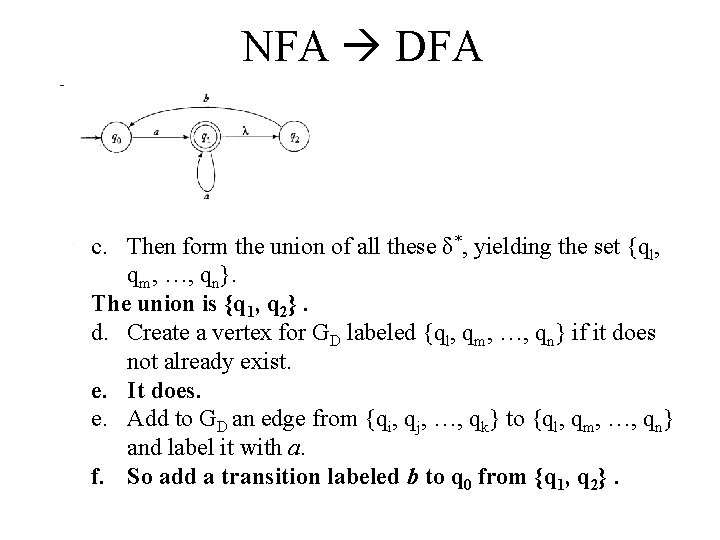
NFA DFA 1. Create a graph GD with vertex {q 0}. Identify this vertex as the initial vertex. 2. Repeat the following steps until no more edges are missing: a. Take any vertex {qi, qj, …, qk} of GD that has no outgoing edge for some a . b. Compute δ* (qi, a), δ* (qj, a), …, δ* (qk, a). c. The form the union of all these δ*, yielding the set {ql, qm, …, qn}. d. Create a vertex for GD labeled {ql, qm, …, qn} if it does not already exist. e. Add to GD an edge from {qi, qj, …, qk} to {ql, qm, …, qn} and label it with a. 3. Every state of GD whose label contains and qf FN is identified as a final vertex. 4. If MN accepts , the vertex q 0 in GD is also made a final vertex.

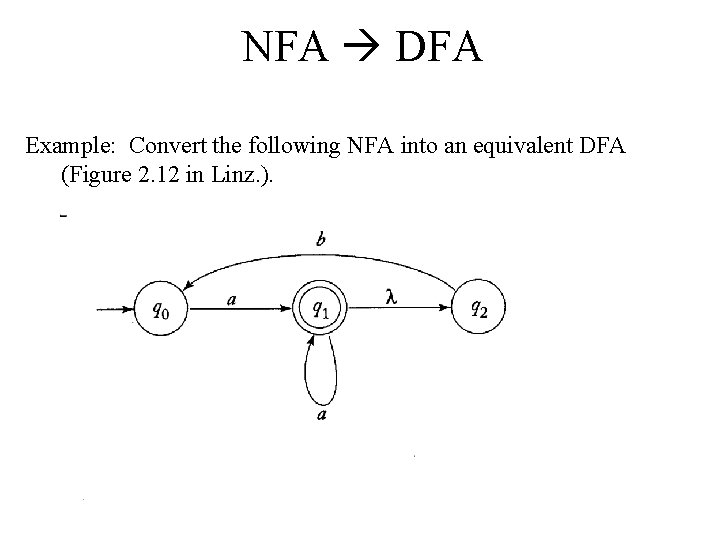
NFA DFA Example: Convert the following NFA into an equivalent DFA (Figure 2. 12 in Linz. ).

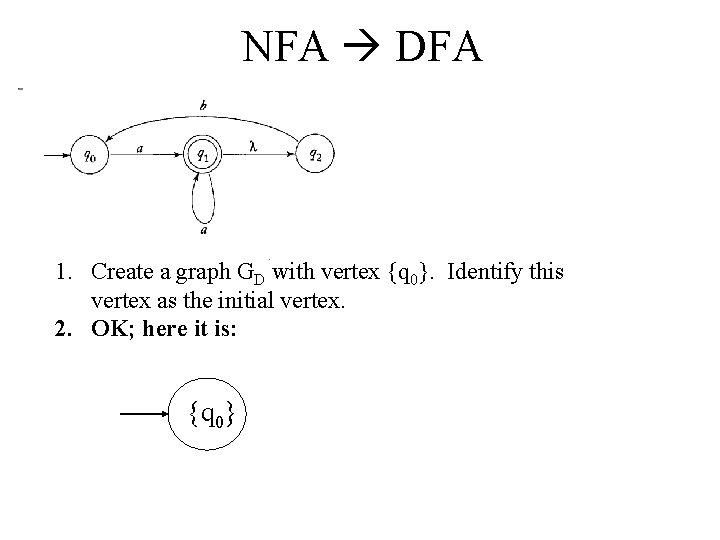
NFA DFA 1. Create a graph GD with vertex {q 0}. Identify this vertex as the initial vertex. 2. OK; here it is: {q 0}

NFA DFA 1. Repeat the following steps until no more edges are missing: a. Take any vertex {qi, qj, …, qk} of GD that has no outgoing edge for some a . b. OK. Vertex q 0 in our new DFA has no outgoing edge for a yet. b. Compute δ* (qi, a), δ* (qj, a), …, δ* (qk, a). OK. From q 0 in our NFA, upon reading an a the extended transition function takes us to state q 1, or we can go on to q 2 (via a “free” lambda-move).

NFA DFA c. Then form the union of all these δ*, yielding the set {ql, qm, …, qn}. So our new DFA will have a state labeled {q 1, q 2}. d. Create a vertex for GD labeled {ql, qm, …, qn} if it does not already exist. So create a vertex for our new DFA and label it {q 1, q 2}. e. Add to GD an edge from {qi, qj, …, qk} to {ql, qm, …, qn} and label it with a. f. So add a transition labeled a to {q 1, q 2} from q 0.

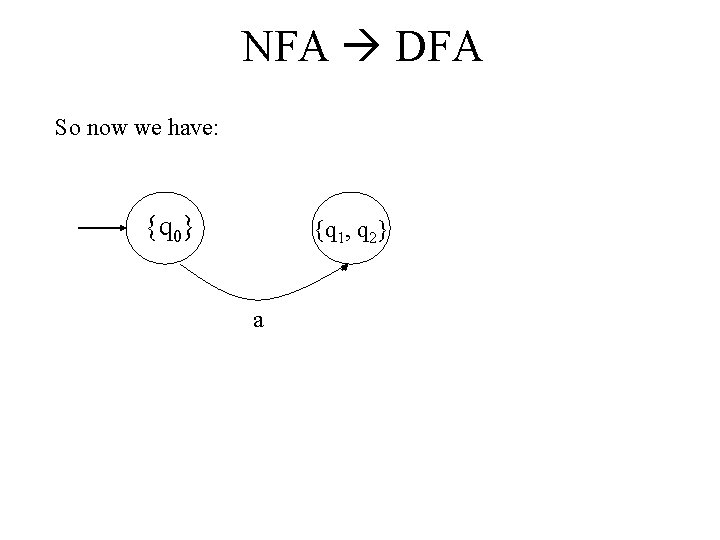
NFA DFA So now we have: {q 0} {q 1, q 2} a

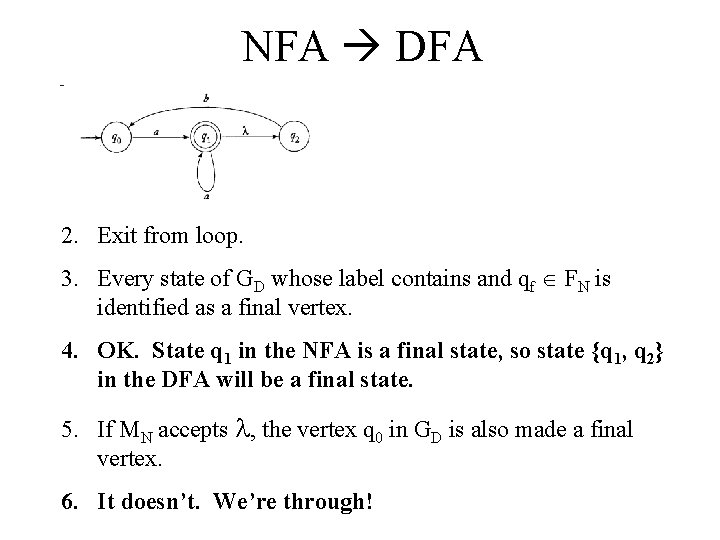
NFA DFA 1. Repeat the following steps until no more edges are missing: a. Take any vertex {qi, qj, …, qk} of GD that has no outgoing edge for some a . b. OK. Vertex q 0 in our new DFA has no outgoing edge for b yet. b. Compute δ* (qi, b), δ* (qj, b), …, δ* (qk, b). Well, there is no transition specified in our NFA from state q 0 upon reading a b. Therefore, δ* ({q 0}, b) = .

NFA DFA c. Then form the union of all these δ*, yielding the set {ql, qm, …, qn}. So our new DFA will have a state labeled . d. Create a vertex for GD labeled {ql, qm, …, qn} if it does not already exist. e. So create a vertex for our new DFA and label it . e. Add to GD an edge from {qi, qj, …, qk} to {ql, qm, …, qn} and label it with a. So add a transition labeled b to from q 0.

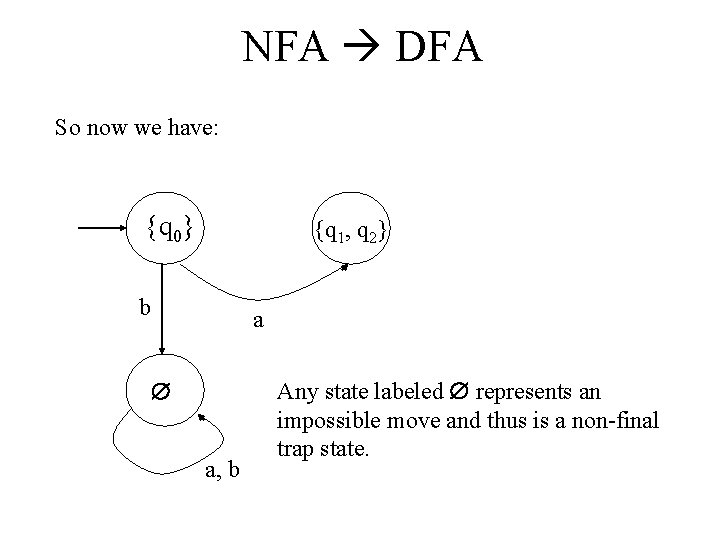
NFA DFA So now we have: {q 0} {q 1, q 2} b a a, b Any state labeled represents an impossible move and thus is a non-final trap state.

NFA DFA 1. Repeat the following steps until no more edges are missing: a. Take any vertex {qi, qj, …, qk} of GD that has no outgoing edge for some a . b. OK. Vertex {q 1, q 2} in our new DFA has no outgoing edge for a yet. b. Compute δ* (qi, b), δ* (qj, b), …, δ* (qk, b). OK. From q 1 in our NFA, upon reading an a the extended transition function leaves us in state q 1, or q 2 via a “free” lambda-move. From q 2 in our NFA, upon reading an a there is no specified transition.

NFA DFA c. Then form the union of all these δ*, yielding the set {ql, qm, …, qn}. The union is {q 1, q 2}. d. Create a vertex for GD labeled {ql, qm, …, qn} if it does not already exist. e. It does. e. Add to GD an edge from {qi, qj, …, qk} to {ql, qm, …, qn} and label it with a. f. So add a transition labeled a to {q 1, q 2} from {q 1, q 2}.

NFA DFA So now we have: a {q 0} b {q 1, q 2} a a, b

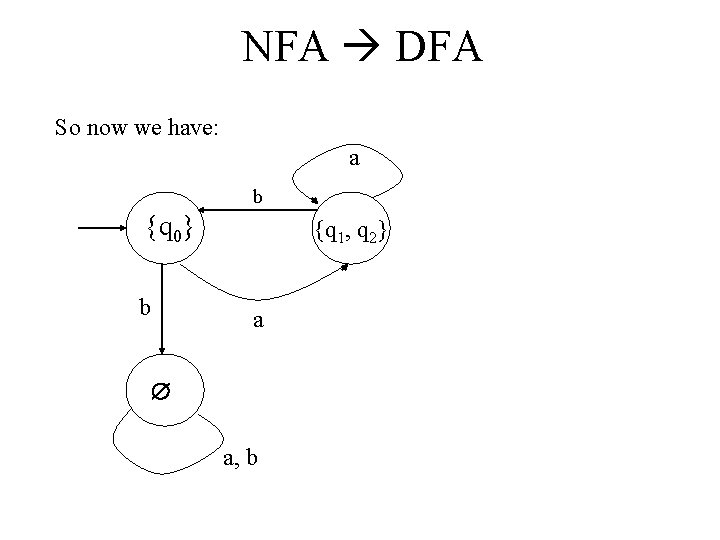
NFA DFA 1. Repeat the following steps until no more edges are missing: a. Take any vertex {qi, qj, …, qk} of GD that has no outgoing edge for some a . b. OK. Vertex {q 1, q 2} in our new DFA has no outgoing edge for b yet. b. Compute δ* (qi, b), δ* (qj, b), …, δ* (qk, b). OK. From q 2 in our NFA, upon reading a b the extended transition function leaves us in state q 0. From q 1 in our NFA, upon reading a b there is no specified transition. However, we can make a free lambda-move to q 2, and thence to q 0.

NFA DFA c. Then form the union of all these δ*, yielding the set {ql, qm, …, qn}. The union is {q 1, q 2}. d. Create a vertex for GD labeled {ql, qm, …, qn} if it does not already exist. e. It does. e. Add to GD an edge from {qi, qj, …, qk} to {ql, qm, …, qn} and label it with a. f. So add a transition labeled b to q 0 from {q 1, q 2}.

NFA DFA So now we have: a b {q 0} b {q 1, q 2} a a, b

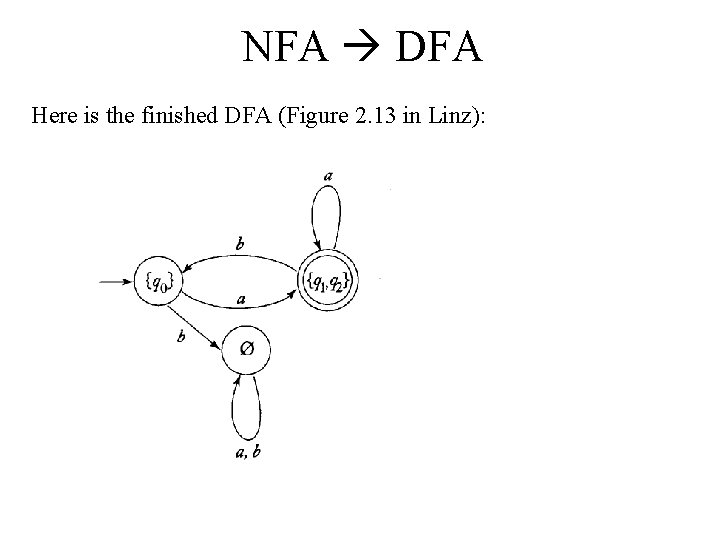
NFA DFA 2. Exit from loop. 3. Every state of GD whose label contains and qf FN is identified as a final vertex. 4. OK. State q 1 in the NFA is a final state, so state {q 1, q 2} in the DFA will be a final state. 5. If MN accepts , the vertex q 0 in GD is also made a final vertex. 6. It doesn’t. We’re through!

NFA DFA Here is the finished DFA (Figure 2. 13 in Linz):

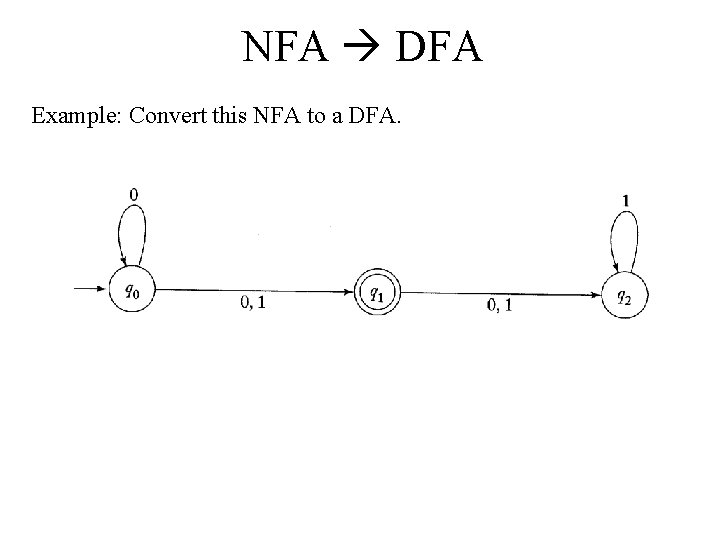
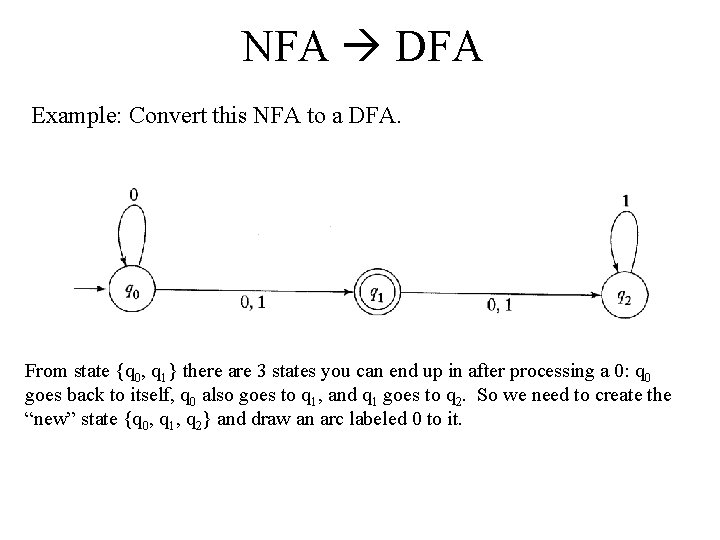
NFA DFA Example: Convert this NFA to a DFA.

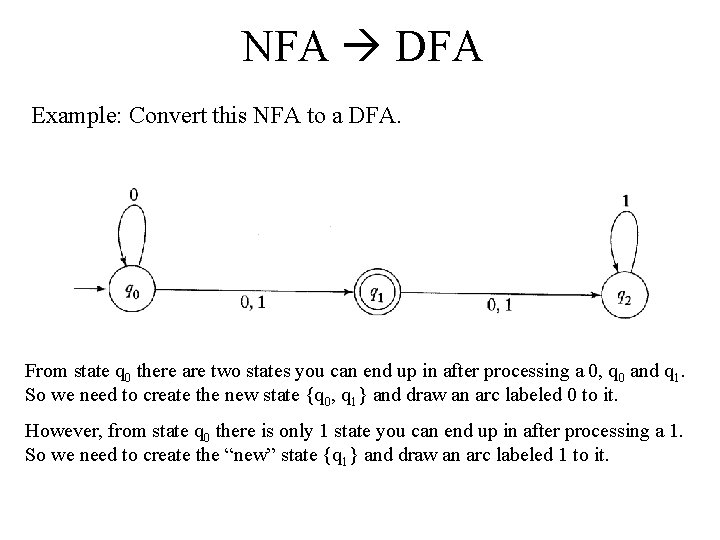
NFA DFA Example: Convert this NFA to a DFA. From state q 0 there are two states you can end up in after processing a 0, q 0 and q 1. So we need to create the new state {q 0, q 1} and draw an arc labeled 0 to it. However, from state q 0 there is only 1 state you can end up in after processing a 1. So we need to create the “new” state {q 1} and draw an arc labeled 1 to it.

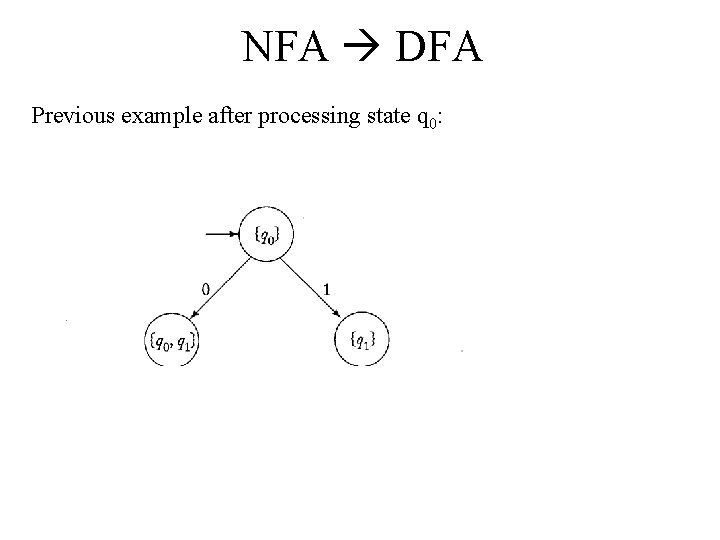
NFA DFA Previous example after processing state q 0:

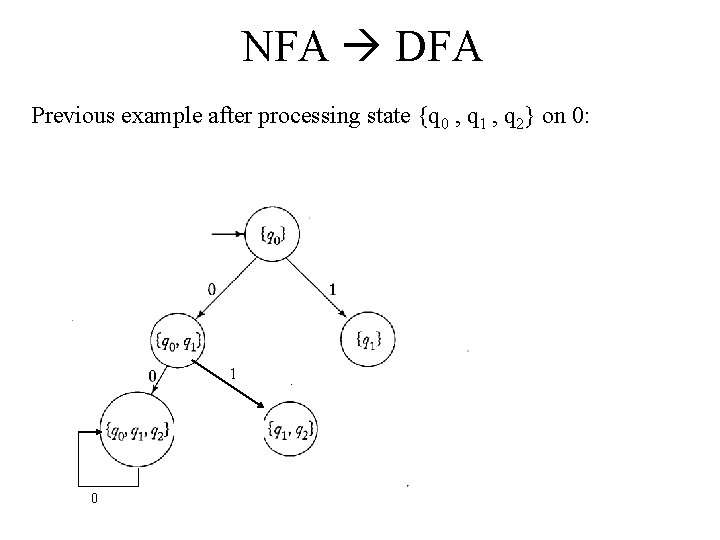
NFA DFA Example: Convert this NFA to a DFA. From state {q 0, q 1} there are 3 states you can end up in after processing a 0: q 0 goes back to itself, q 0 also goes to q 1, and q 1 goes to q 2. So we need to create the “new” state {q 0, q 1, q 2} and draw an arc labeled 0 to it.

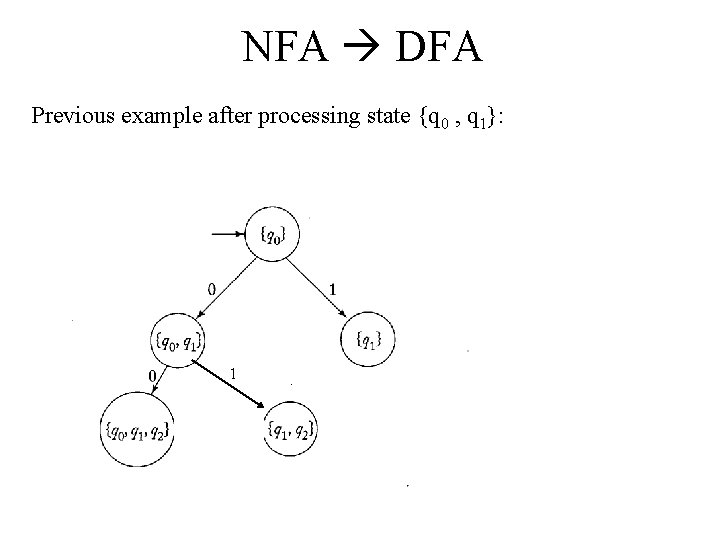
NFA DFA Previous example after processing state {q 0 , q 1} on 0:

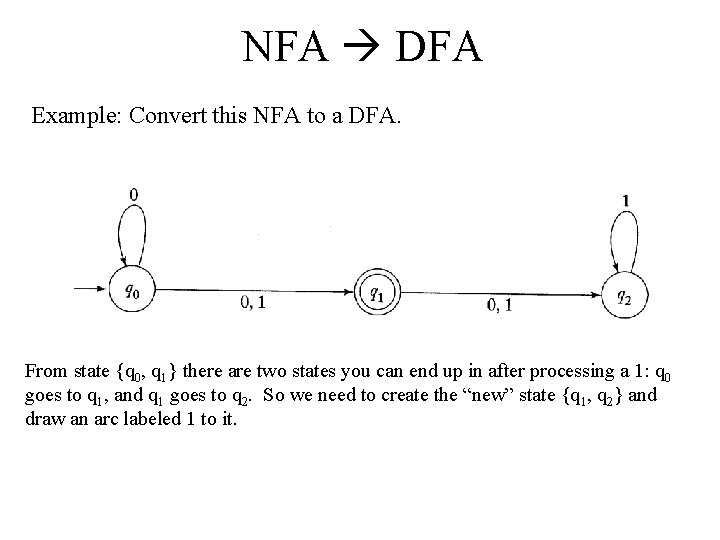
NFA DFA Example: Convert this NFA to a DFA. From state {q 0, q 1} there are two states you can end up in after processing a 1: q 0 goes to q 1, and q 1 goes to q 2. So we need to create the “new” state {q 1, q 2} and draw an arc labeled 1 to it.

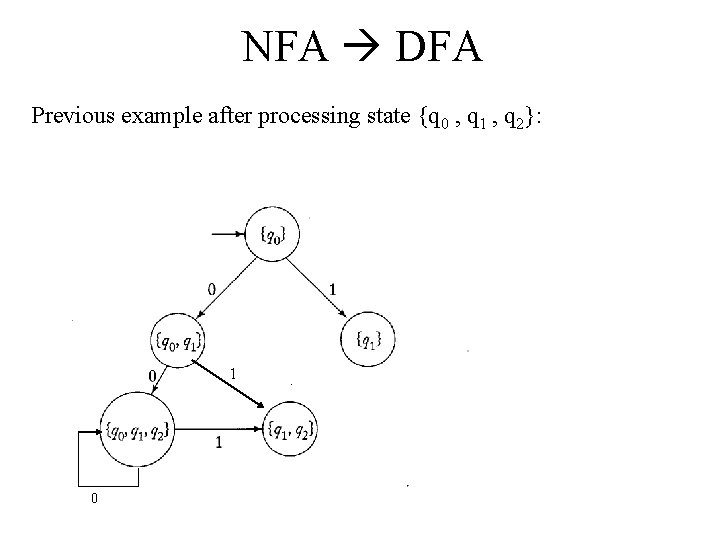
NFA DFA Previous example after processing state {q 0 , q 1}: 1

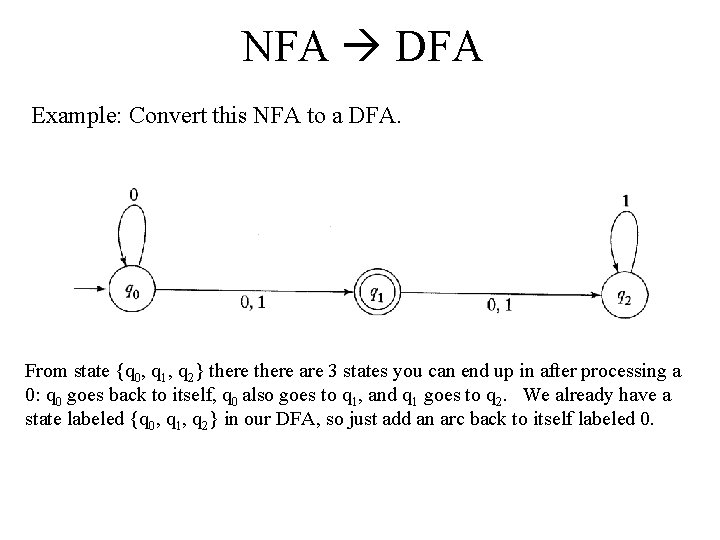
NFA DFA Example: Convert this NFA to a DFA. From state {q 0, q 1, q 2} there are 3 states you can end up in after processing a 0: q 0 goes back to itself, q 0 also goes to q 1, and q 1 goes to q 2. We already have a state labeled {q 0, q 1, q 2} in our DFA, so just add an arc back to itself labeled 0.

NFA DFA Previous example after processing state {q 0 , q 1 , q 2} on 0: 1 0

NFA DFA Example: Convert this NFA to a DFA. From state {q 0, q 1, q 2} there are 2 states you can end up in after processing a 1: q 0 goes to q 1, q 1 goes to q 2, and q 2 goes back to itself. We already have a state labeled {q 1, q 2} in our DFA, so just add an arc to it labeled 1.

NFA DFA Previous example after processing state {q 0 , q 1 , q 2}: 1 0

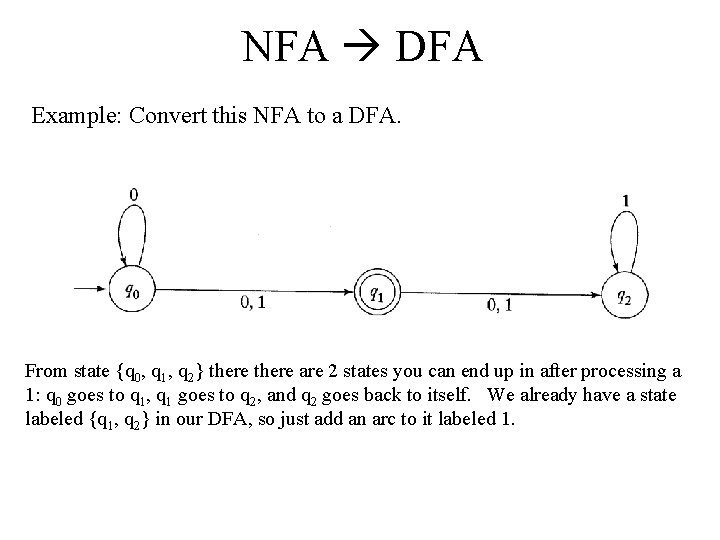
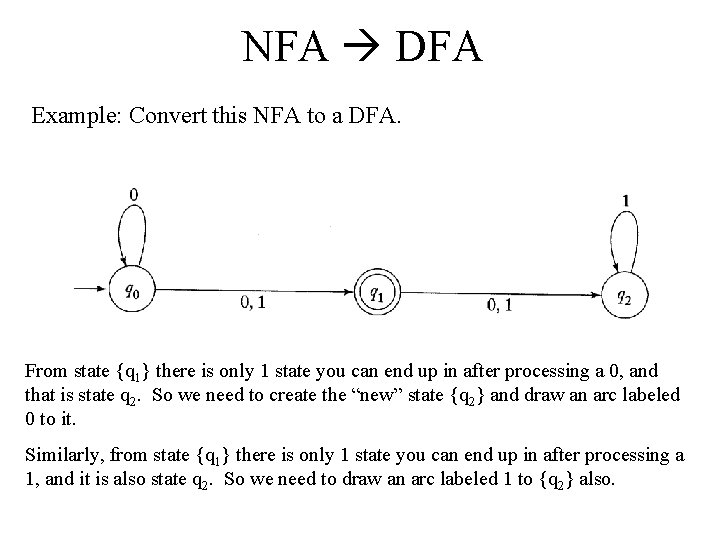
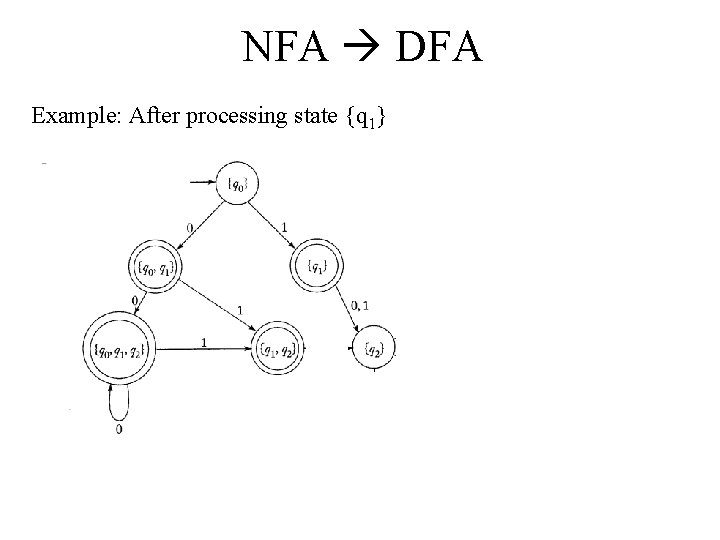
NFA DFA Example: Convert this NFA to a DFA. From state {q 1} there is only 1 state you can end up in after processing a 0, and that is state q 2. So we need to create the “new” state {q 2} and draw an arc labeled 0 to it. Similarly, from state {q 1} there is only 1 state you can end up in after processing a 1, and it is also state q 2. So we need to draw an arc labeled 1 to {q 2} also.

NFA DFA Example: After processing state {q 1}

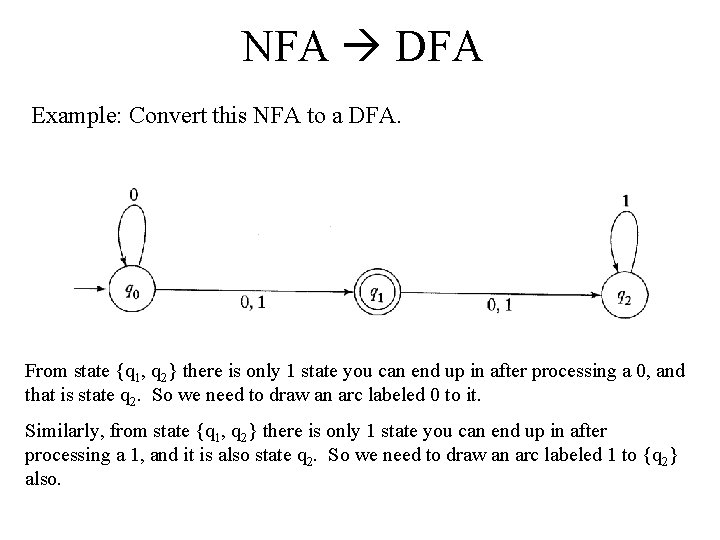
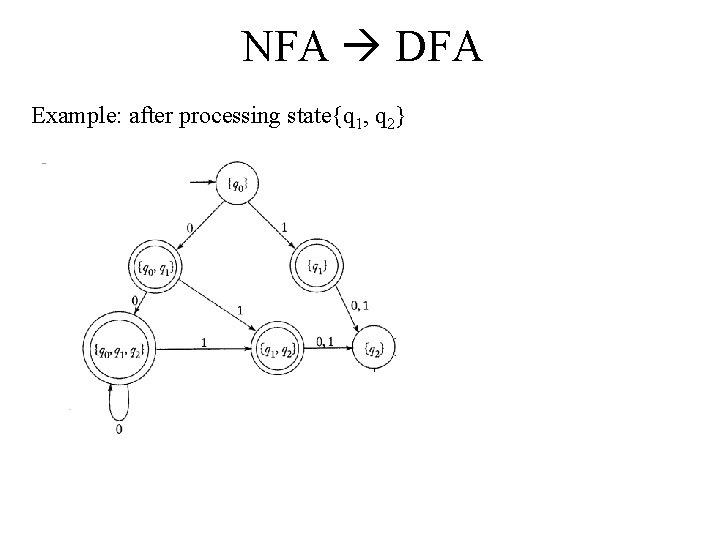
NFA DFA Example: Convert this NFA to a DFA. From state {q 1, q 2} there is only 1 state you can end up in after processing a 0, and that is state q 2. So we need to draw an arc labeled 0 to it. Similarly, from state {q 1, q 2} there is only 1 state you can end up in after processing a 1, and it is also state q 2. So we need to draw an arc labeled 1 to {q 2} also.

NFA DFA Example: after processing state{q 1, q 2}

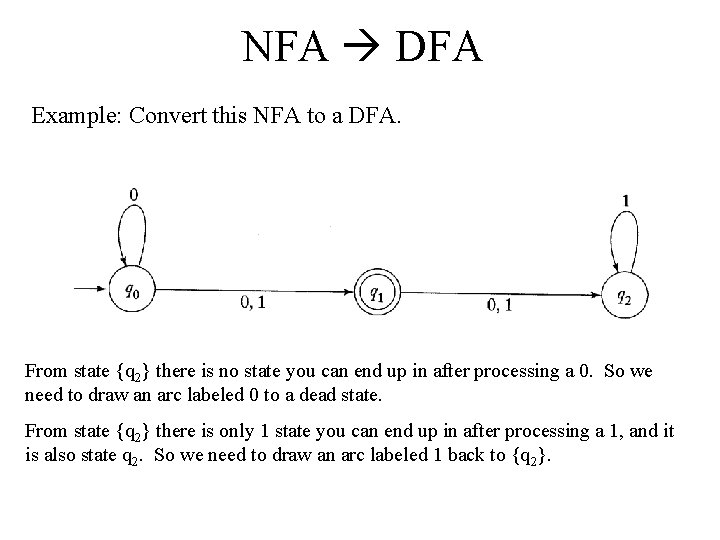
NFA DFA Example: Convert this NFA to a DFA. From state {q 2} there is no state you can end up in after processing a 0. So we need to draw an arc labeled 0 to a dead state. From state {q 2} there is only 1 state you can end up in after processing a 1, and it is also state q 2. So we need to draw an arc labeled 1 back to {q 2}.

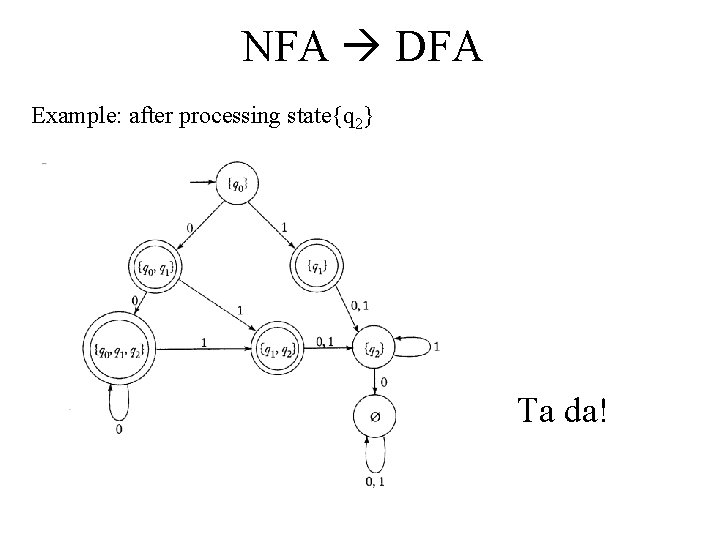
NFA DFA Example: after processing state{q 2} Ta da!

Minimal DFA’s Two states p and q of a DFA are called indistinguishable if * (p, w) F implies * (q, w) F , and * (p, w) F implies * (q, w) F , for all w *. If there exists some string w * such that * (p, w) F and * (q, w) F or vice versa, then the states p and q are said to be distinguishable by string w.

The “Mark” procedure This procedure marks all pairs of distinguishable states. 1. Remove all inaccessible states. 2. Consider all pairs of states (p, q). If p F and q F or vice versa, mark the pair (p, q) as distinguishable. 3. Repeat the following step until no previously unmarked pairs are marked: For all pairs (p, q) and all a , compute (p, a) = pa and (q, a) = qa. If the pair (pa, qa) is marked as distinguishable, mark (p, q) as distinguishable.

The “Reduce” procedure Given a DFA M = (Q, , , q 0, F), we construct a reduced DFA M’ = (Q’, , ’, q 0’, F’) as follows: 1. Use procedure Mark to find all pairs of distinguishable states. Then from this find the sets of indistinguishable states by partitioning the state set Q of the DFA into disjoint subsets {qi, qj, …, qk}, {ql, qm, …, qn}, …, such that: • any q Q occurs in exactly one of these subsets, • elements in each subset are indistinguishable, and • any two elements from different subsets are distinguishable.

The “Reduce” procedure, cont. 2. For each set {qi, qj, …, qk} of such indistinguishable states, create a state labeled ij…k for M’. 3. For each transition rule of M of the form (qr, a) = qp, find the sets to which qr and qp belong. If qr {qi, qj, …, qk} and qp {ql, qm, …, qn}, add to ’ a rule: 4. ’ (ij…k, a) = lm…n. 4. The initial state q 0’ is that state of M’ whose label includes the 0. 5. F’ is the set of all the states whose label contains i such that qi F.

Theorem 2. 4 Given any DFA M, application of the procedure Reduce yields another DFA M’ such that L(M) = L(M’) Furthermore, M’ is minimal in the sense that there is no other DFA with a smaller number of states which also accepts L(M).

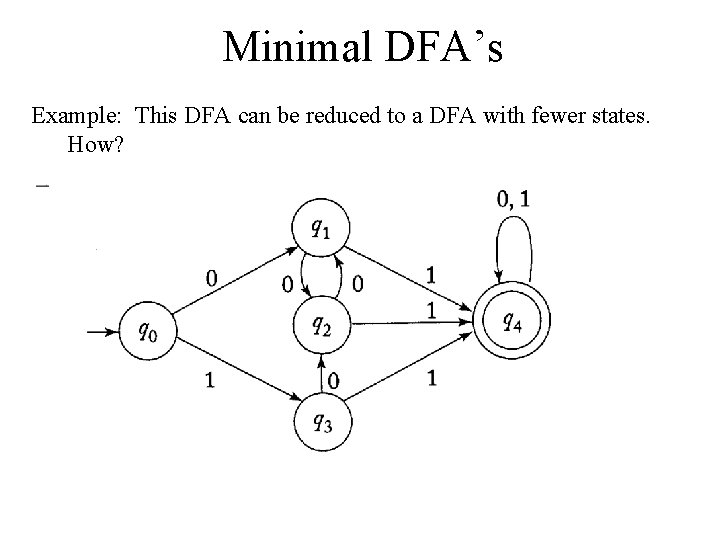
Minimal DFA’s Example: This DFA can be reduced to a DFA with fewer states. How?

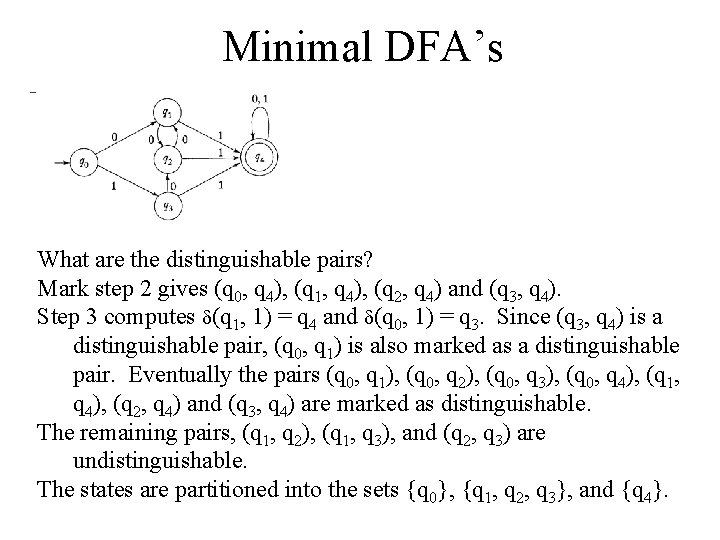
Minimal DFA’s What are the distinguishable pairs? Mark step 2 gives (q 0, q 4), (q 1, q 4), (q 2, q 4) and (q 3, q 4). Step 3 computes (q 1, 1) = q 4 and (q 0, 1) = q 3. Since (q 3, q 4) is a distinguishable pair, (q 0, q 1) is also marked as a distinguishable pair. Eventually the pairs (q 0, q 1), (q 0, q 2), (q 0, q 3), (q 0, q 4), (q 1, q 4), (q 2, q 4) and (q 3, q 4) are marked as distinguishable. The remaining pairs, (q 1, q 2), (q 1, q 3), and (q 2, q 3) are undistinguishable. The states are partitioned into the sets {q 0}, {q 1, q 2, q 3}, and {q 4}.

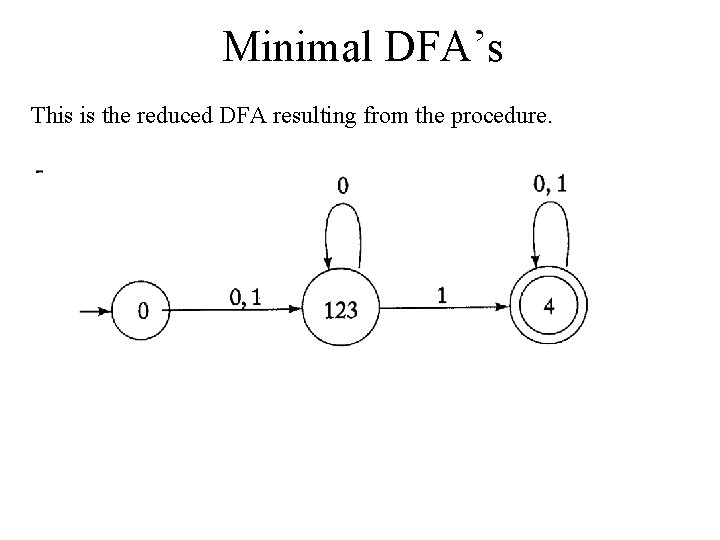
Minimal DFA’s This is the reduced DFA resulting from the procedure.

Minimum number of states in an FA If there are n distinguishable strings in a language, then there must be at least n states in the finite automata that accepts it. The FA has no memory, other than the current state. This puts a lower bound on the number of states in a FA recognizing a language. A Finite Automaton is finite; that is, it cannot have infinitely many states.

Next chapter Read chapter 3, Regular languages and regular grammars
 Gtg stands for in automata
Gtg stands for in automata Csci 3130
Csci 3130 Formal languages and automata theory tutorial
Formal languages and automata theory tutorial Csc3120 datasheet
Csc3120 datasheet Automata theory tutorial
Automata theory tutorial Automata theory tutorial
Automata theory tutorial Cse 340 principles of programming languages
Cse 340 principles of programming languages Vineeth kashyap
Vineeth kashyap Formal and informal difference
Formal and informal difference Characteristics of formal style
Characteristics of formal style Formal relational query languages
Formal relational query languages Formal relational query languages
Formal relational query languages Formal query language in dbms
Formal query language in dbms Introduction to scripting languages
Introduction to scripting languages Introduction to programming languages
Introduction to programming languages Informal schooling meaning
Informal schooling meaning Unit 1 formal informal and non formal education
Unit 1 formal informal and non formal education Difference between formal education and als
Difference between formal education and als Ejemplos de lenguaje formal e informal
Ejemplos de lenguaje formal e informal Contoh falsafah
Contoh falsafah Karangan formal
Karangan formal Pola komunikasi ke atas
Pola komunikasi ke atas Maksud falasi
Maksud falasi Keperluan esteem
Keperluan esteem Aap1 - linguagem e oralidade
Aap1 - linguagem e oralidade Persamaan paud formal dan nonformal
Persamaan paud formal dan nonformal What is the concept of valid and invalid alphabets
What is the concept of valid and invalid alphabets Central concepts of automata theory
Central concepts of automata theory Reduksi dfa
Reduksi dfa Cis262
Cis262 Real-time systems and programming languages
Real-time systems and programming languages Cs 421
Cs 421 Modern languages for life and work
Modern languages for life and work Media and information languages
Media and information languages What is front end compiler
What is front end compiler Proto language
Proto language Defence centre for languages and culture
Defence centre for languages and culture Strongly typed vs weakly typed
Strongly typed vs weakly typed List the primitives that specify a data mining task.
List the primitives that specify a data mining task. Media and information literacy performance task
Media and information literacy performance task Advantages and disadvantages of programming languages
Advantages and disadvantages of programming languages Sound devices in a poem
Sound devices in a poem Real time programming language
Real time programming language Decision properties of cfl
Decision properties of cfl Closure properties of cfl
Closure properties of cfl Regular and irregular languages
Regular and irregular languages Translators and facilities of languages
Translators and facilities of languages School of languages cultures and societies
School of languages cultures and societies Cs 421 uiuc
Cs 421 uiuc Data mining languages and system architecture
Data mining languages and system architecture Cross-lingual name tagging and linking for 282 languages
Cross-lingual name tagging and linking for 282 languages Introduction in email
Introduction in email Formal writing introduction
Formal writing introduction Deterministic finite automaton
Deterministic finite automaton 2 stack pda
2 stack pda Contoh ekspresi reguler
Contoh ekspresi reguler Bahasa automata
Bahasa automata Uts teori bahasa dan otomata
Uts teori bahasa dan otomata Grammar in levels
Grammar in levels Automata
Automata Pushdown automata
Pushdown automata Language definition
Language definition Pda automata
Pda automata Push down automata adalah
Push down automata adalah Expressions grammar
Expressions grammar Nfa non deterministic finite automata
Nfa non deterministic finite automata Dfa ndfa
Dfa ndfa Linear bounded automaton is a:
Linear bounded automaton is a: Invatare automata
Invatare automata Gtg
Gtg Mealy machine
Mealy machine Npda automata
Npda automata Simple grammar automata
Simple grammar automata Finite state automata (fsa) adalah
Finite state automata (fsa) adalah Felina hungária kft
Felina hungária kft Julius richard büchi
Julius richard büchi Pushdown automata exercises solutions
Pushdown automata exercises solutions Lexical analysis finite automata
Lexical analysis finite automata Dfa state diagram generator
Dfa state diagram generator Bidirectional transducers in automata theory
Bidirectional transducers in automata theory Pushdown automata implementation
Pushdown automata implementation Pushdown automata implementation
Pushdown automata implementation Instantaneous description of pda
Instantaneous description of pda Regex compile
Regex compile Maquina de moore
Maquina de moore Cellular automata matlab
Cellular automata matlab Linear bounded automata solved examples
Linear bounded automata solved examples Concatenation of two finite automata examples
Concatenation of two finite automata examples Infinite automata
Infinite automata Fsa dinyatakan dalam 5 tupel, kecuali
Fsa dinyatakan dalam 5 tupel, kecuali Transition graph to regular expression examples
Transition graph to regular expression examples Finite automata tutorial
Finite automata tutorial Testare automata
Testare automata Csci 3130
Csci 3130 Automata theory
Automata theory




















































































































