Teori Matematika terhadap materi teori bahasa dan automata

Teori Matematika terhadap materi teori bahasa dan automata Pertemuan 1 Mahasiswa mampu menjelaskan Kedudukan Teori Bahasa Automata pada ilmu Komputer

Materi • Pengenalan bahasa dan Automata • Himpunan • Fungsi • Relasi • Graph • Konsep Bahasa dan Automata • Hirarki Chomsky

Pengenalan bahasa dan Automata Teori bahasa dan automata merupakan bagian ilmu komputer berupa model dam gagasan yang mendasari mengenasi komputasi. Automata adalah mesin abstrak yang dapat mengenali (recognize), menerima (accept), atau membangkitkan (generate) sebuah kalimat dalam bahasa tertentu.

Beberapa Pengertian Dasar

Operasi dasar String

Operasi dasar string

Himpunan adalah sebuah kumpulan dari elemen Dapat ditulis

himpunan C = { a, b, c, d, e, f, g, h, i, j, k } C = { a, b, …, k } S = { 2, 4, 6, … } finite set S = { j : j > 0, and j = 2 k for some k>0 } S = { j : j is nonnegative and even } infinite set 8

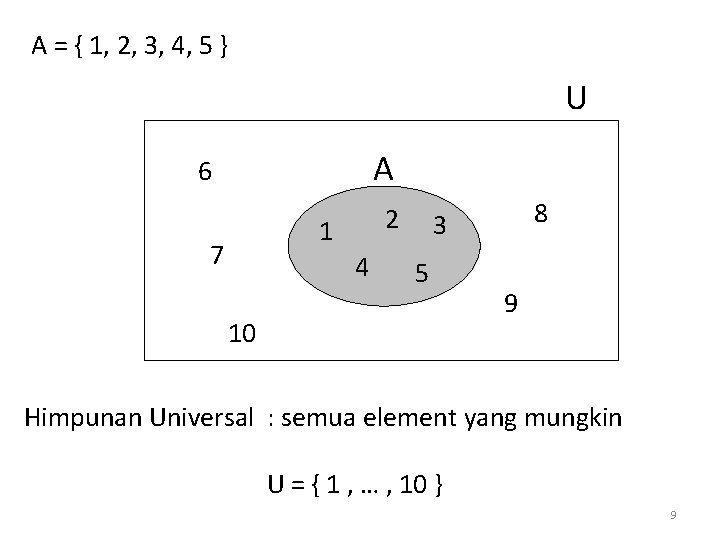
A = { 1, 2, 3, 4, 5 } U A 6 2 1 7 4 8 3 5 10 9 Himpunan Universal : semua element yang mungkin U = { 1 , … , 10 } 9

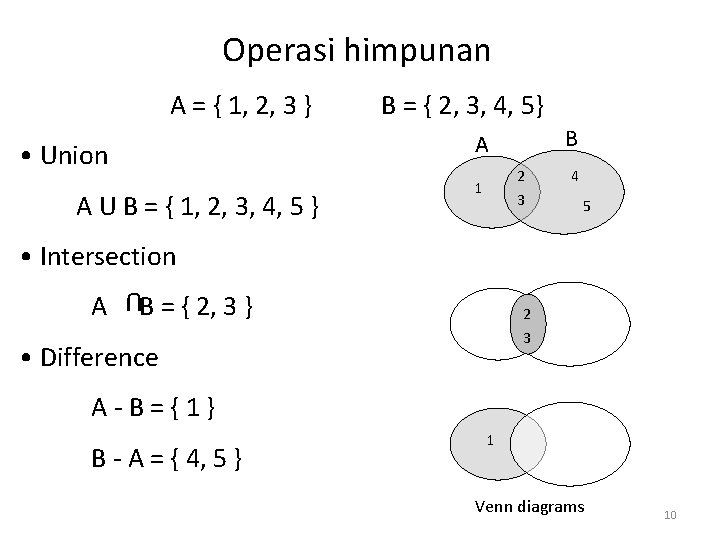
Operasi himpunan A = { 1, 2, 3 } B = { 2, 3, 4, 5} B A • Union A U B = { 1, 2, 3, 4, 5 } 2 3 1 4 5 • Intersection U A B = { 2, 3 } 2 3 • Difference A-B={1} B - A = { 4, 5 } 1 Venn diagrams 10

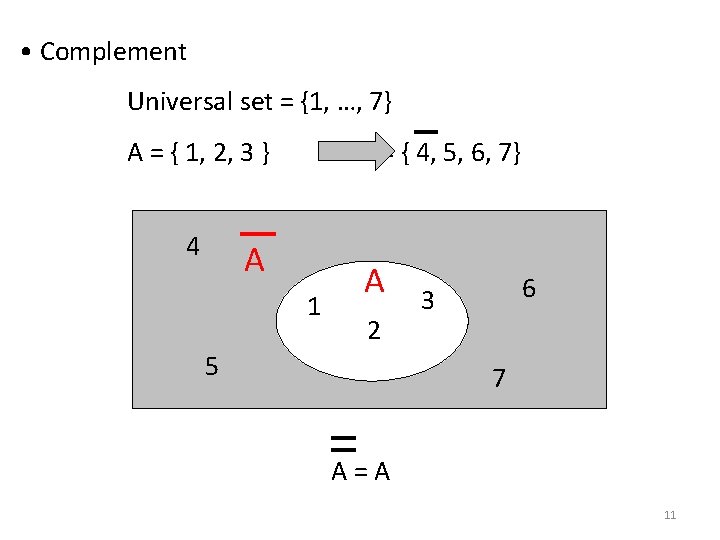
• Complement Universal set = {1, …, 7} A = { 1, 2, 3 } 4 A = { 4, 5, 6, 7} A 1 A 2 5 6 3 7 A=A 11

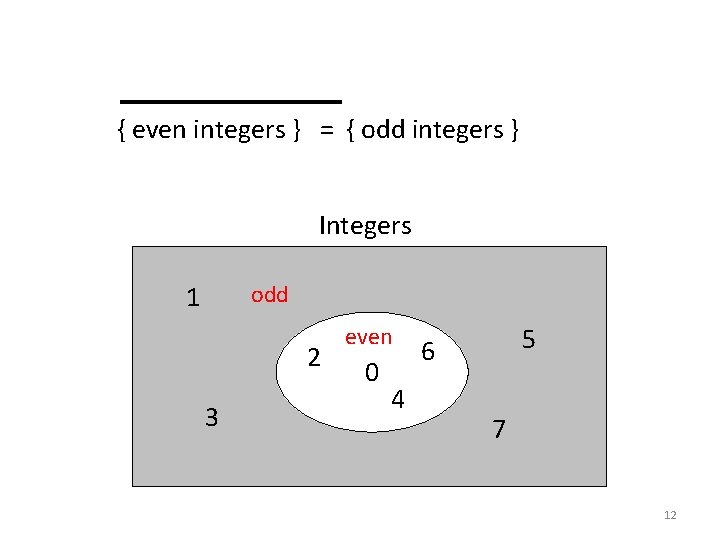
{ even integers } = { odd integers } Integers 1 odd 2 3 even 0 4 5 6 7 12

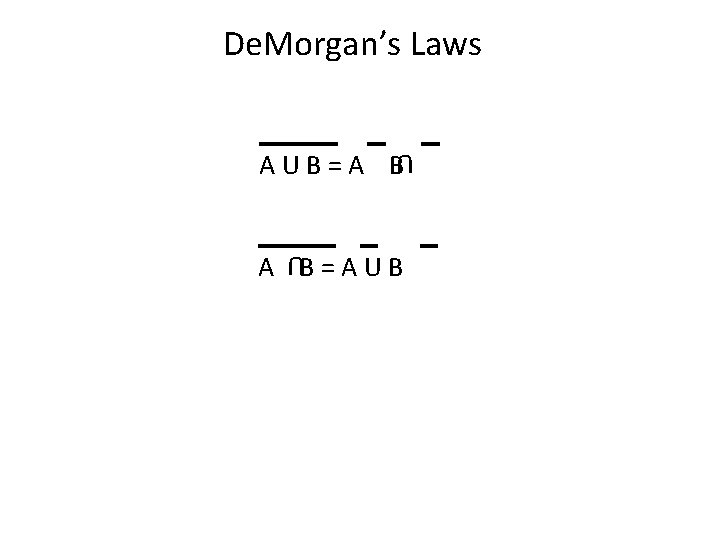
De. Morgan’s Laws AUB=A B U A B=AUB U

Empty, Null Set: ={} SU S- U S =S = = Universal Set =S -S= 14

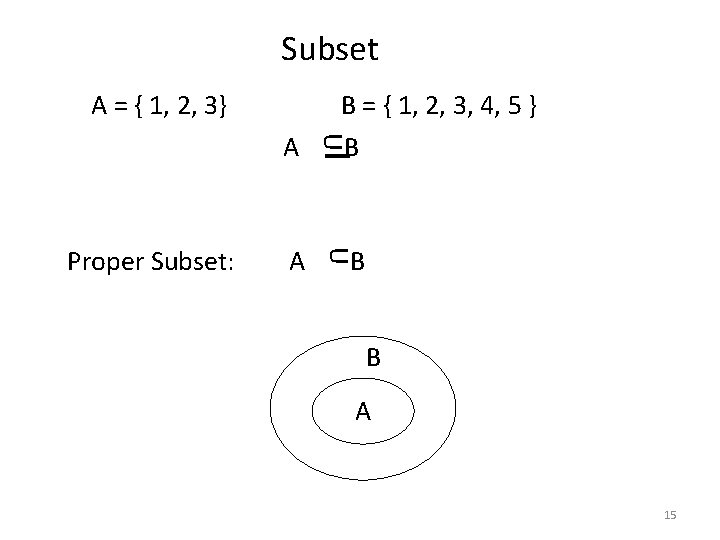
Subset A = { 1, 2, 3} A B U Proper Subset: U A B = { 1, 2, 3, 4, 5 } B B A 15

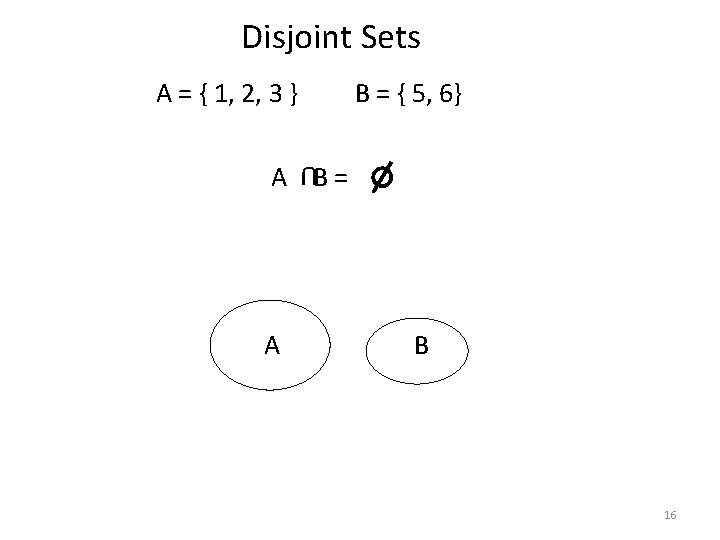
Disjoint Sets A = { 1, 2, 3 } B = { 5, 6} A B= U A B 16

Set Cardinality • For finite sets A = { 2, 5, 7 } |A| = 3 (panjang himpunan) 17

Himpunan bagian adalah sebuah bagian himpunan Dari sebuah himpunan S = { a, b, c } 2 S = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } Observation: | 2 S | = 2|S| ( 8 = 23 ) 18

Cartesian Product A = { 2, 4 } B = { 2, 3, 5 } A X B = { (2, 2), (2, 3), (2, 5), ( 4, 2), (4, 3), (4, 5) } |A X B| = |A| |B| 19

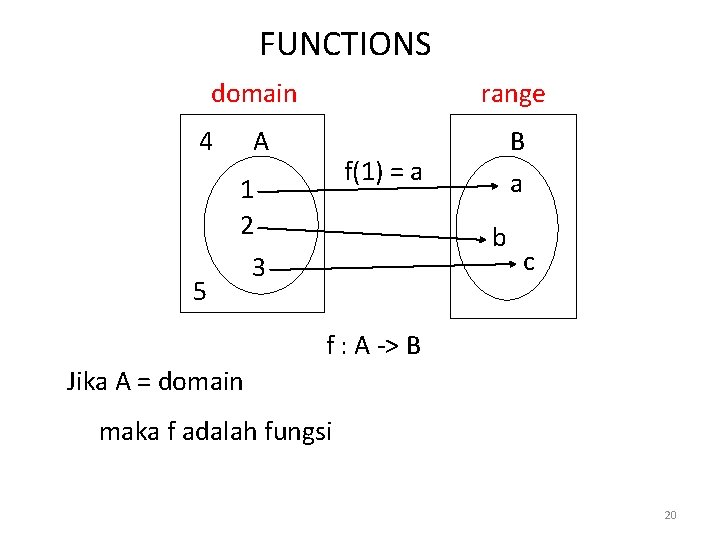
FUNCTIONS domain 4 range A f(1) = a 1 2 5 B a b 3 c f : A -> B Jika A = domain maka f adalah fungsi 20

RELATIONS R = {(x 1, y 1), (x 2, y 2), (x 3, y 3), …} xi R y i Jika R = ‘>’: 2 > 1, 3 > 2, 3 > 1 21

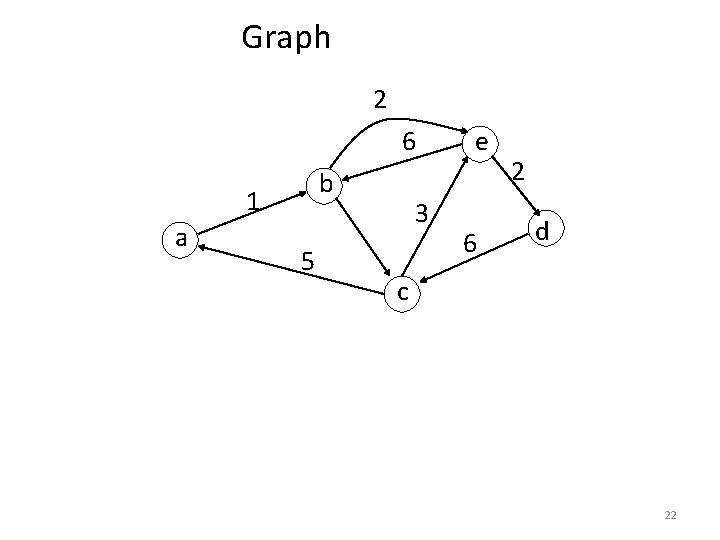
Graph 2 6 b 1 a 5 3 e 6 2 d c 22

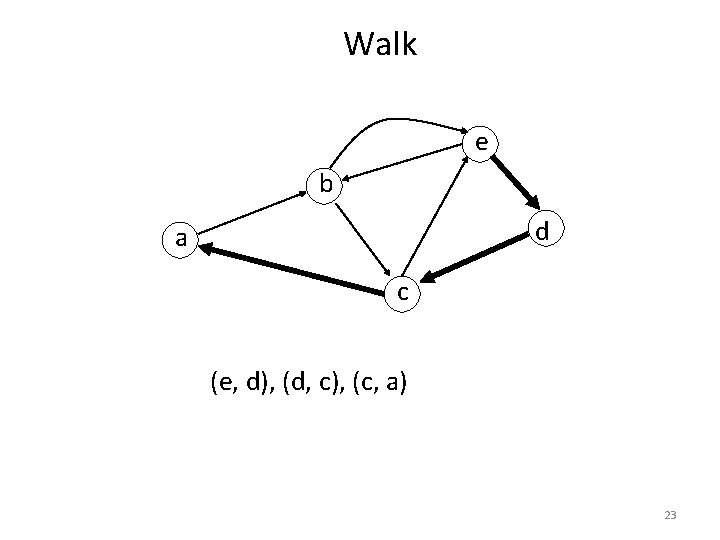
Walk e b d a c (e, d), (d, c), (c, a) 23

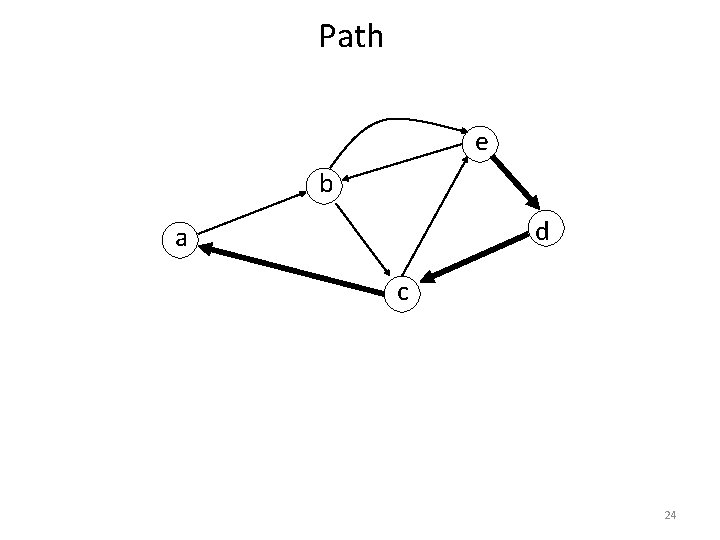
Path e b d a c 24

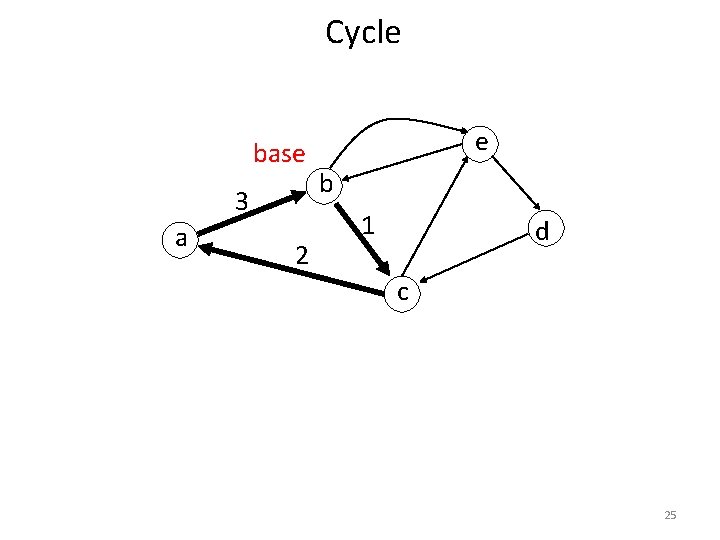
Cycle base 3 a 2 e b 1 d c 25

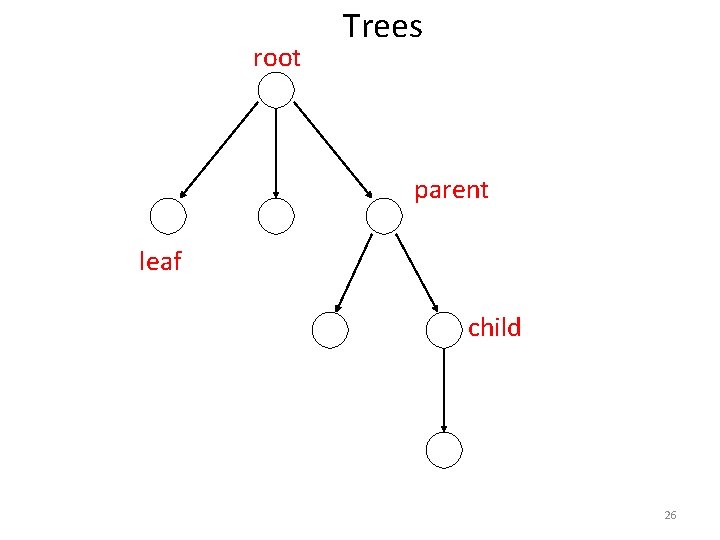
root Trees parent leaf child 26

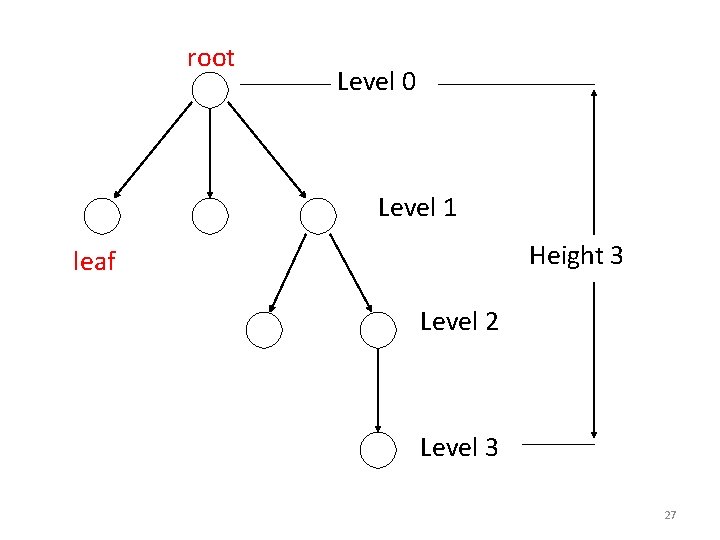
root Level 0 Level 1 Height 3 leaf Level 2 Level 3 27

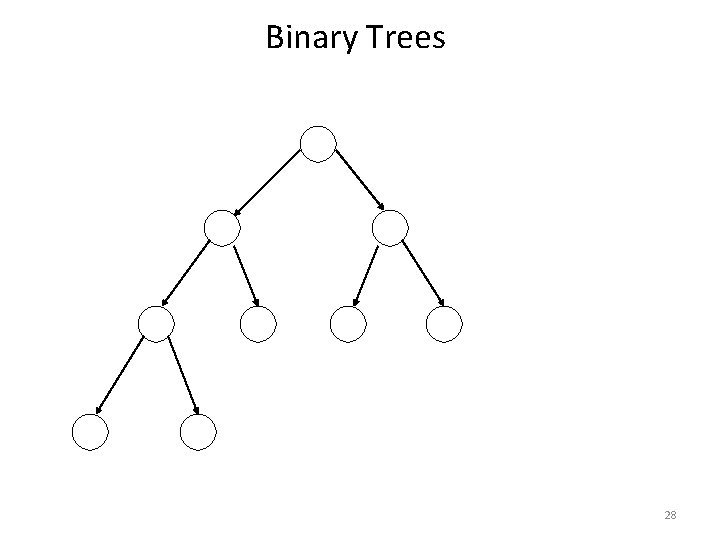
Binary Trees 28

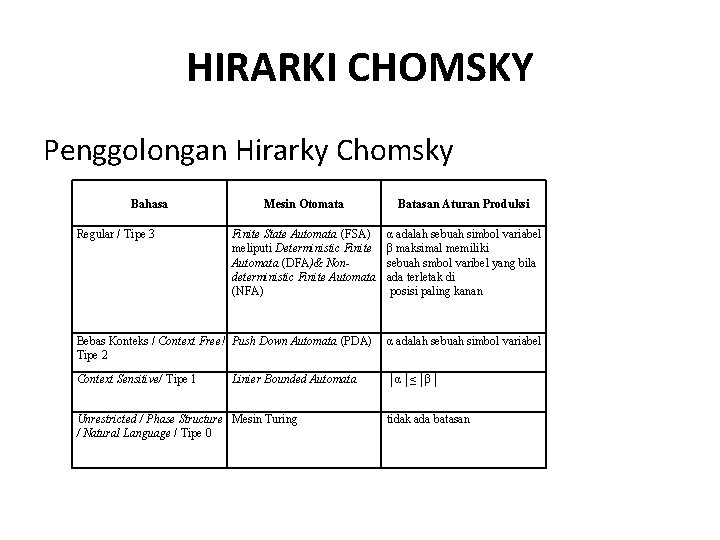
HIRARKI CHOMSKY Penggolongan Hirarky Chomsky Bahasa Mesin Otomata Batasan Aturan Produksi Finite State Automata (FSA) meliputi Deterministic Finite Automata (DFA)& Nondeterministic Finite Automata (NFA) α adalah sebuah simbol variabel β maksimal memiliki sebuah smbol varibel yang bila ada terletak di posisi paling kanan Bebas Konteks / Context Free! Push Down Automata (PDA) Tipe 2 α adalah sebuah simbol variabel Context Sensitive/ Tipe 1 │α│≤│β│ Regular / Tipe 3 Linier Bounded Automata Unrestricted / Phase Structure Mesin Turing / Natural Language / Tipe 0 tidak ada batasan